Главная

Задача 1. Исследование плоского напряженного состояния.

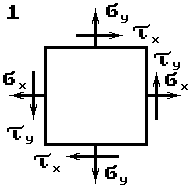
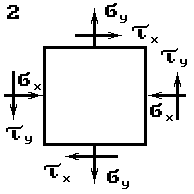
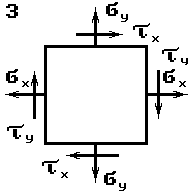
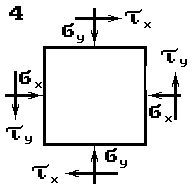
Стальной кубик (рис.1) находится под действием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю). Требуется найти:

1. главные напряжения и направление главных площадок;

2. максимальные касательные напряжения, равные наибольшей разности главных напряжений;

3. главные деформации

4. эквивалентное напряжение по четвертой (энергетической) теории прочности;

5. относительное изменение объема;

6. удельную потенциальную энергию деформации.

Данные взять из табл.1.

Таблица 1

Номер cтроки	Схема по рис.1	σx	σy	τx
01	1	10	50	20
02	2	20	60	90
03	3	30	70	100
04	4	40	80	10
05	5	50	90	60
06	6	60	100	70
07	7	70	60	80
08	8	80	70	90
09	9	90	80	40
10	10	100	90	50
11	11	60	100	90
12	12	70	40	100
13	13	80	50	10
14	14	90	90	20
15	15	100	100	90
16	16	10	10	90
17	17	20	20	100
18	18	30	90	10
19	19	40	100	20
20	20	50	10	90
21	21	90	20	100
22	22	100	40	10
23	23	10	50	20
24	24	20	90	40
25	25	30	100	80
26	26	80	80	90
27	27	90	90	100
28	28	100	100	10
29	29	10	10	20
30	30	20	20	40
31	31	40	40	80
32	32	50	50	90
33	33	90	90	100
34	34	100	50	10
35	35	10	90	20
36	36	20	100	40
	а	г	б	а

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13 схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис. 1

Задача 2. Исследование плоского напряженного состояния.

На расчетной схеме (рис.2) указаны две элементарные площадки, на гранях которых возникают нормальные и касательные напряжения.

Требуется для схемы а):

1. Указать главную площадку общего положения.

2. На главной площадке присвоить главным напряжениям соответствующие индексы.

3. По главным напряжениям определить нормальные и касательные напряжения в площадке, положение которых задается нормалью n.

Требуется для схемы б):

1. По напряжениям, заданным на площадке общего положения, определить главные напряжения и их направление.

2. Решение задачи выполнить аналитически и с использованием кругов Мора.

Примечание:

Данные для решения взять согласно ниже приведенных расчетных схем из табл. 2.

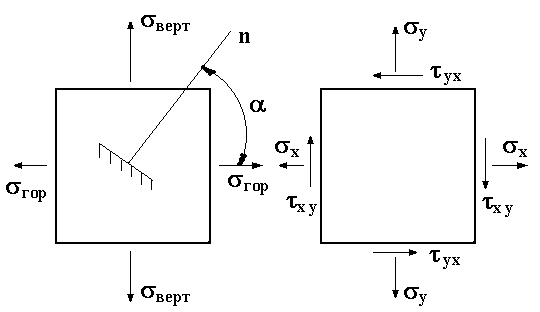
а) б)

Рис. 2.

Таблица 2

Номер строки	Числовые данные вариантов
	σгор, МПа	σверт, МПа	α, град.	σx, МПа	σy, МПа	τxy, МПа
01	-20	-48	60	46	0	-14
02	18	-40	-45	30	0	-50
03	0	40	-40	0	-41	-13
04	46	30	-45	50	20	30
05	-30	-50	45	42	0	32
06	0	-40	-70	20	40	-40
07	0	50	50	28	20	-38
08	49	30	-50	-50	0	-12
09	-20	-48	-40	0	33	21
10	-39	0	-20	0	-12	22
11	48	20	30	0	22	-23
12	20	-47	60	-30	21	18
13	19	-39	60	50	-10	-60
14	40	44	-30	15	0	36
15	47	-30	-45	-28	56	-15
16	0	-44	60	26	-44	11
17	30	0	-60	-20	25	16
18	-18	49	30	-10	-50	-20
19	0	25	-70	-35	0	-61
20	-45	0	30	40	-30	40
21	0	-32	-20	-58	-20	17
22	-20	50	-60	-22	0	41
23	0	-31	60	40	-18	-45
24	49	0	40	-40	20	-30
25	26	40	30	62	32	24
26	-5	-50	30	25	-15	50
27	-35	0	-40	0	-60	-20
28	23	0	20	0	35	28
29	20	0	-45	-12	-39	-19
30	47	40	60	0	30	-40
	в	а	г	б	в	а

Задача 3. Исследование плоского напряженного состояния.

Стальная пластинка (рис.3) с указанными в таблице 3 размерами, находится под действием сил, создающих плоское напряженное состояние. Дано E=1000 МПа, μ=0,3.

Требуется найти:

1. Напряжения σ_x, σ_y, σ, τ_xy, τ.

2. Максимальные напряжения σ_max, σ_min.

3. Деформации ε_x, ε_y.

Данные взять из табл.3.

Таблица 3

Номер cтроки	Номер схемы по рис.3	BF, см	BD, см
01	1	4	3
02	2	8	6
03	3	3	3
04	4	4	3
05	5	3	3
06	6	4	3
07	7	8	6
08	8	3	3
09	9	4	3
10	10	3	3
11	11	4	3
12	12	8	6
13	13	3	3
14	14	4	3
15	15	3	3
16	16	4	3
17	17	8	6
18	18	3	3
19	19	4	3
20	20	3	3
21	21	4	3
22	22	8	6
23	23	3	3
24	24	4	3
25	25	3	3
26	26	4	3
27	27	8	6
28	28	3	3
29	29	4	3
30	30	3	3
31	31	4	3
32	32	8	6
33	33	3	3
34	34	4	3
35	35	3	3
36	36	8	6
	г	в	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

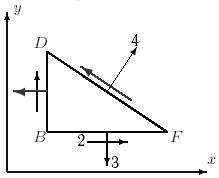
29 схема 30 схема

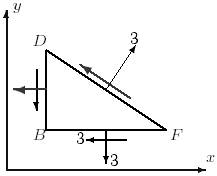
31 схема 32 схема

33 схема 34 схема

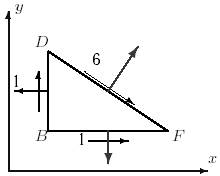
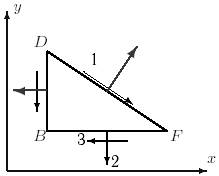
35 схема 36 схема

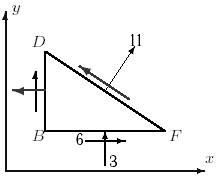
Рис.3

Задача 4. Исследование плоского напряженного состояния по заданным напряжениям на произвольных площадках. Проверка прочности

Исходные данные к задаче выбираются по табл. 4 и схемам на рис. 4.

1. Найдите нормальное, касательное и полное напряжения на наклонной площадке.

2. Найдите величины главных напряжений и угол наклона главных площадок к заданным площадкам. Покажите главные площадки с действующими на них напряжениями на рисунке.

3. Определите величины наибольших касательных напряжений: наибольшего касательного напряжения для заданного плоского напряженного состояния (max τ) и максимального касательного напряжения для заданного элементарного параллелепипеда (т.е. полученного при исследовании объемного напряженного состояния – τ_max). Покажите на рисунке площадки, на которых действуют эти напряжения (max τ и τ_max). Найдите нормальные напряжения на этих площадках.

4. Проверьте прочность материала заданного элементарного параллелепипеда. Найдите действительный коэффициент запаса прочности. Покажите на рисунке опасные площадки.

5. Найдите величины относительных продольных деформаций по главным направлениям и относительную объемную деформацию. Покажите деформации на рисунке.

6*. Постройте следы предельных поверхностей, соответствующие используемым теориям прочности. Покажите точку, изображающую заданное напряженное состояние, найдите графически действительный коэффициент запаса прочности.

Примечание. Пункты 1–3 следует выполнить двумя способами: аналитическим и графическим.

Таблица 4

Номер строки	№ схемы на рис.4	σx, МПа	σz, МПа	τxz, МПа	β, град	σпред, МПа	Материал
01	1	10	-20	30	15	240	Сталь
02	2	-20	30	-40	30	180/600	Чугун
03	3	50	40	50	45	150	Бронза
04	4	-30	-50	-60	60	150/500	Чугун
05	1	-10	30	10	75	210	Дюралюмин.
06	2	20	-40	-20	15	160/480	Чугун
07	3	-70	-60	20	30	260	Сталь
08	4	40	30	-10	45	120	Бронза
09	4	-80	70	-30	60	180/600	Чугун
10	3	60	-30	40	75	200	Дюралюмин.
	г	в	а	б	г	в	а

1 схема 2 схема

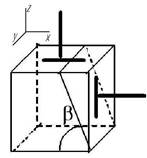
3 схема 4 схема

Рис. 4

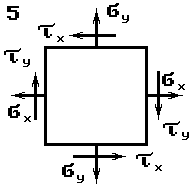
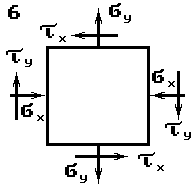
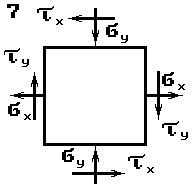
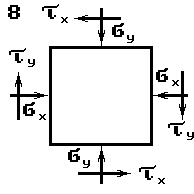
Задача 5. Исследование плоского напряженного состояния по заданным напряжениям на главных площадках. Проверка прочности

Исходные данные к задаче выбираются по табл. 5 и схемам на рис. 5.

1. По заданным главным напряжениям найдите нормальные и касательные напряжения на наклонной площадке.

2. Определите величины наибольших касательных напряжений: наибольшего касательного напряжения для заданного плоского напряженного состояния max τ и максимального касательного напряжения для заданного элементарного параллелепипеда τ_max (т.е. полученного при исследовании объемного напряженного состояния). Покажите на рисунке площадки, на которых они действуют. Найдите нормальные напряжения на этих площадках.

3. Проверьте прочность материала заданного элементарного параллелепипеда. Найдите действительный коэффициент запаса прочности. Покажите на рисунке опасные площадки.

4. Найдите компоненты тензора деформаций для заданного напряженного состояния. Покажите деформации на рисунке.

5*. Постройте следы предельных поверхностей, соответствующие используемым теориям прочности. Покажите точку, изображающую заданное напряженное состояние, найдите графически действительный коэффициент запаса прочности.

Примечание. Пункты 1 и 2 следует выполнить двумя способами: аналитическим и графическим.

Таблица 5

Номер строки	№ схемы на рис. 5	, МПа	β, град	, МПа	σпред, МПа	Материал
01	4	50	75	40	180/600	Чугун
02	3	-100	45	-50	150	Бронза
03	2	80	60	-30	150/450	Чугун
04	1	-80	30	30	240	Сталь
05	4	-90	15	-10	180/600	Чугун
06	3	20	30	60	200	Дюралюмин.
07	2	-110	15	-120	160/500	Чугун
08	1	10	60	-10	180/540	Чугун
09	1	-70	75	-20	260	Сталь
10	2	0	30	-60	150/450	Чугун
	в	г	б	а	в	г

1 схема 2 схема

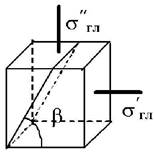
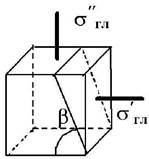
3 схема 4 схема

Рис.5

Примеры выполнения задач

Пример 1

Дано: = -25 МПа; = -75 МПа; = 20 МПа; = 55°; для чугуна = 80 Мпа; рис.6.

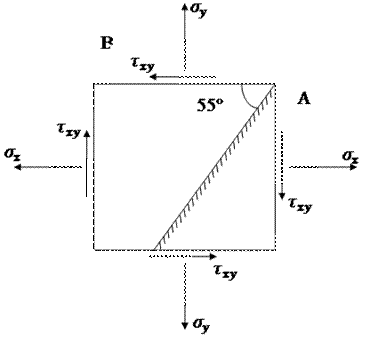
Рис.6

Решение.

1. По заданным напряжениям, действующим по граням элемента, определим главные напряжения с помощью круга Мора (рис.7). Напряженное состояние в какой-либо площадке можно представить точкой в координатной плоскости , а напряженное состояние в двух взаимно-перпендикулярных площадках соответствует двум точкам, расположенных на концах диаметра круга Мора. Поэтому для построения круга Мора отложим в системе координат точку, соответствующую напряженному состоянию в грани А, и точку, соответствующую напряженному состоянию в грани В.

Соединив точки А и В прямой линией, получим диаметр круга Мора, пересечение которого с осью дает центр круга Мора. Пересечение окружности, проведенной из центра С радиусом СА, с осью дает значение главных напряжений и в окрестности выделенного элемента.

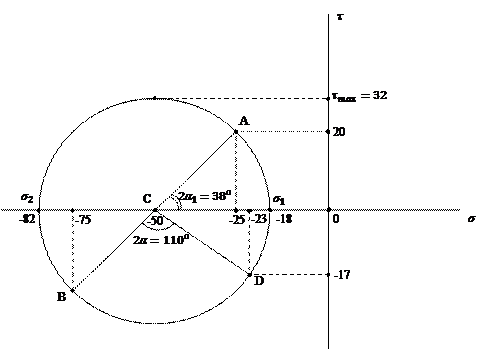
Рис.7

Из круга Мора получаем:

= -18 МПа; = -82 МПа.

Наибольшие касательные напряжения будут равны = 32МПа. Для определения напряжения в площадке, наклонной под углом = 55° к горизонтальной площадке В, надо от точки В отложить против часовой стрелки центральный угол = 110°. Тогда координаты точки D и будут напряжениями в площадке . Окончательно получим:

= -23 МПа; = -17 МПа.

2. Теперь определим аналитически, чему равны главные напряжения и наибольшие касательные напряжения по формулам:

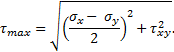
Подставляя исходные данные, получим:

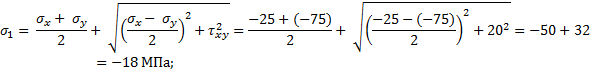
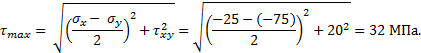
что совпадает со значениями напряжений, снятых с круга Мора.

3. Покажем на схеме положение главных площадок и направление главных напряжений (рис.8). Для того, чтобы от площадки А перейти к площадке, где действует главное напряжение , нужно совершить поворот по часовой стрелке на угол . Поэтому на схеме от площадки А откладываем по часовой стрелке угол и получаем площадку, в которой действует главное напряжение . В перпендикулярной ей площадке действует главное напряжение . Так как и является отрицательными величинами, то они вызывают сжатие на своих площадках.

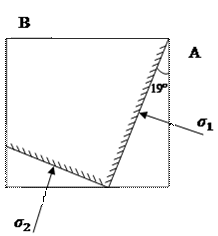
Рис.8

4. Проверим прочность материала по критерию наибольших касательных напряжений, который иногда называется третьей теорией прочности, по формуле:

,

где R – расчетное сопротивление материала при одноосном растяжении.

Подставляем в формулу и для той заданной площадки, в которой действует большее по модулю нормальное напряжение и . В нашем случае это площадка В. Подставляя значения и в исходную формулу, получим:

Следовательно, величины напряжений, действующих по заданным площадкам, являются недопустимыми для данного материала с точки зрения его прочности.

Пример 2

Рассмотрим случай плоского напряженного состояния в точке: МПа, МПа, МПа (рис. 9,а).

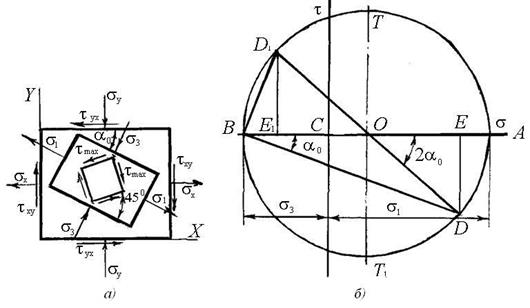
Рис.9

Решение.

Растягивающие напряжения положительны и направлены от сечения, сжимающие отрицательны и направлены к сечению. Положительные касательные напряжения направлены по часовой стрелке, отрицательные — против. Согласно закону парности касательных напряжений . Поэтому направляем против часовой стрелки, а - по часовой. Напряженное состояние в точке изображено в виде прямоугольника с напряжениями

Значения главных напряжений определим по формуле

Поскольку , то МПа, МПа.

Положение главной площадки находим по формуле

На рисунке 9,а отложим угол по часовой стрелке относительно оси Х (угол отрицательный). Это одна из главных площадок, вторая перпендикулярна ей.

Главное напряжение действует на второй главной площадке, так как проекции на нормаль направлены от площадки, главное напряжение - на первой, расположенной под углом к оси Х. На прямоугольнике, представляющем главные площадки, изображаем главные напряжения .

Наибольшие касательные напряжения определим по формуле

Они действуют на площадках, расположенных под углом 45° к главным площадкам и направлены так, чтобы проекции их на нормаль к главной площадке с вызывали растяжение. Изображаем их на прямоугольнике, расположенном под углом 45° к главным площадкам.

Построим круг Мора (см. рис. 9,б). проводим оси координат σ-τ. По оси абсцисс откладываем значения (соответственно точки Е и Е₁). Из точки Е по оси ординат откладываем значение (оно отрицательно) и находим точку D, лежащую на окружности. Из точки Е₁ откладываем значение (оно положительно) и находим точку D₁. Соединив точки D и D₁ прямой, определим центр круга - точку С и радиус круга - отрезок CD. Проведем круг. Отрезок ОА представляет собой наибольшее главное напряжение , отрезок ОВ - наименьшее главное напряжение . Отрезки СТ и СТ₁ представляют собой наибольшие касательные напряжения. Соединив точку В прямыми с точками D и D₁ мы получим главные площадки ВD и ВD₁.

Онлайн-калькулятор "Расчет по различным теориям прочности"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00