Главная

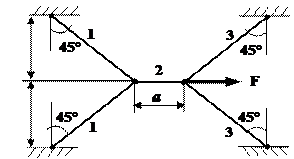
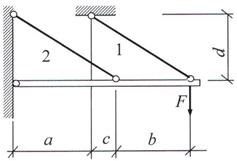
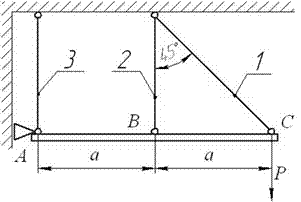
Задача 1. Статически неопределимые стержневые системы растяжения-сжатия.

Составить полную систему уравнений для определения усилий в стержнях заданной стержневой системы.

Данные взять из табл.1 и рис.1.

Таблица 1

Номер cтроки	Схема по рис.1
01	1
02	2
03	3
04	4
05	5
06	6
07	7
08	8
09	9
10	10
11	11
12	12
13	13
14	14
15	15
16	16
17	17
18	18
19	19
20	20
21	21
22	22
23	23
24	24
25	25
26	26
27	27
28	28
29	29
30	30
31	31
32	32
33	33
34	34
35	35
36	36
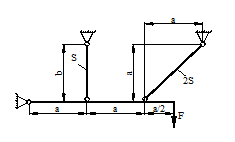
	а

1 схема 2 схема 3 схема

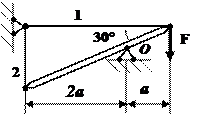
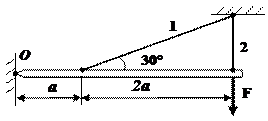
4 схема 5 схема 6 схема

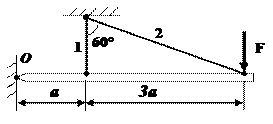
7 схема 8 схема 9 схема

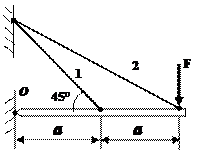
10 схема 11 схема 12 схема

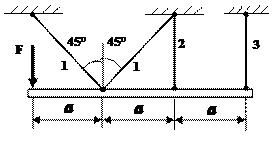
13 схема 14 схема 15 схема

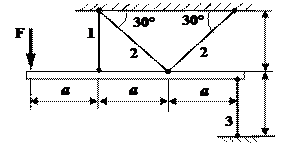
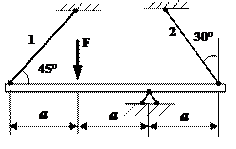
16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

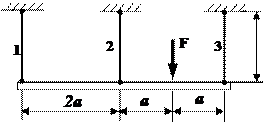
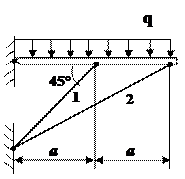
25 схема 26 схема 27 схема

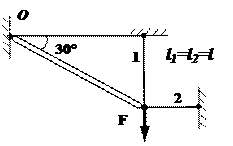
28 схема 29 схема 30 схема

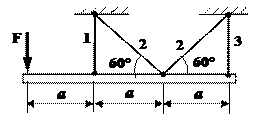
31 схема 32 схема 33 схема

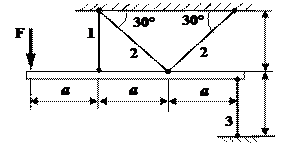
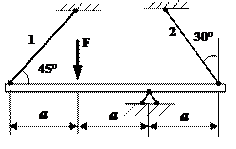
34 схема 35 схема 36 схема

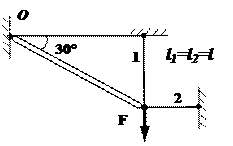
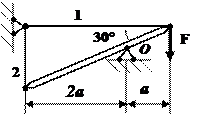
Рис. 1

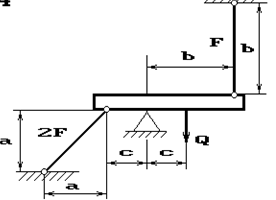
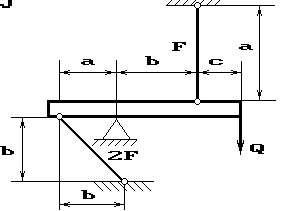
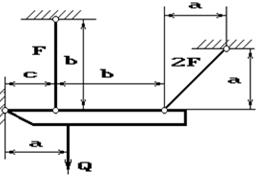
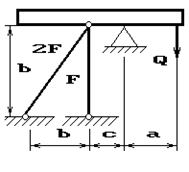
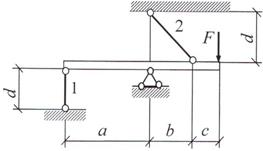
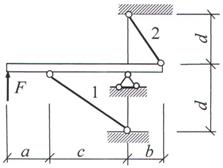
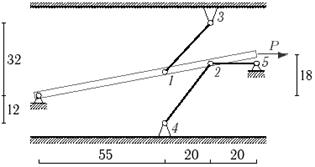
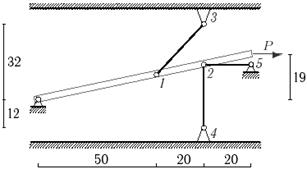
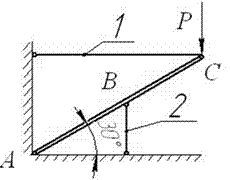
Задача 2. Статически неопределимые стержневые системы растяжения-сжатия.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис.2).

Требуется найти:

1) усилия и напряжения в стержнях, выразив их через силу Q;

2) допускаемую нагрузку Q_adm, приравняв большее из напряжений в двух стержнях допускаемому напряжению σ_adm=160 МПа;

Данные взять из табл.2.

Таблица 2

Номер cтроки	Схема по рис.2	F, см^2	а, м	b, м	с, м	Q, кН
01	1	11	2	2,1	2,4	100
02	2	12	2,1	2,2	2,2	120
03	3	13	2,2	2,3	2,5	130
04	4	14	2,4	2,4	2,7	140
05	5	15	2,6	2,5	2,5	150
06	6	16	2,8	2,6	2,1	160
07	7	17	2,8	2,7	2,5	170
08	8	18	2,7	2,8	2,9	180
09	9	19	2,9	2,9	2,0	180
10	10	20	2,4	3,0	2,6	200
11	11	11	2,6	2,5	2,1	100
12	12	12	2,8	2,6	2,2	120
13	13	13	2,8	2,7	2,3	130
14	14	14	2,7	2,8	2,4	140
15	15	15	2,9	2,9	2,5	150
16	16	16	2	3,0	2,6	160
17	17	17	2,1	2,1	2,7	170
18	18	18	2,2	2,2	2,8	180
19	19	19	2,4	2,3	2,9	180
20	20	20	2,6	2,4	3,0	200
21	21	11	2,8	2,5	2,1	100
22	22	12	2,8	2,4	2,2	120
23	23	13	2,7	2,6	2,3	130
24	24	14	2,9	2,8	2,4	140
25	25	15	2	2,8	2,5	150
26	26	16	2,1	2,7	2,6	160
27	27	17	2,2	2,9	2,7	170
28	28	18	2,4	2,0	2,8	180
29	29	19	2,6	2,2	2,9	180
30	30	20	2,8	2,3	3,0	200
31	31	15	2,8	2,4	2,2	100
32	32	16	2,7	2,5	2,3	120
33	33	17	2,9	2,6	2,4	130
34	34	18	2,2	2,8	2,5	140
35	35	19	2,4	2,9	2,6	150
36	36	20	2,6	3,0	2,7	160
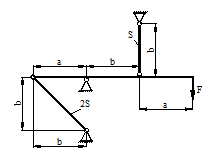
	б	а	в	б	г	а

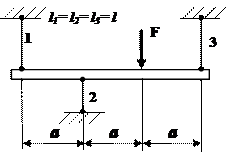
1 схема 2 схема 3 схема

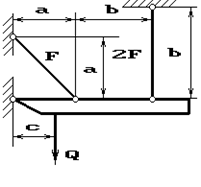
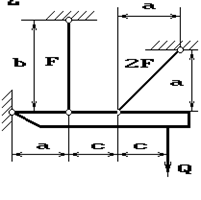
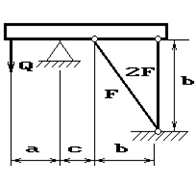
4 схема 5 схема

6 схема 7 схема

8 схема 9 схема 10 схема

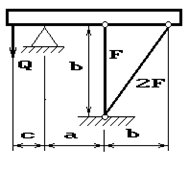
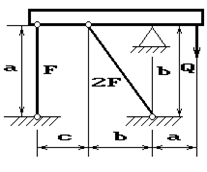
11 схема 12 схема 13 схема

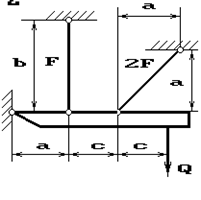
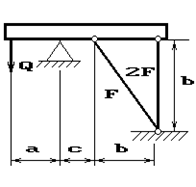
14 схема 15 схема

16 схема 17 схема

18 схема 19 схема 20 схема

21 схема 22 схема 23 схема

24 схема 25 схема

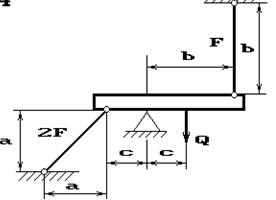
26 схема 27 схема

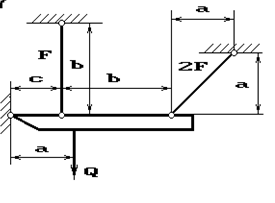
28 схема 29 схема 30 схема

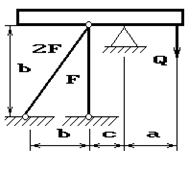
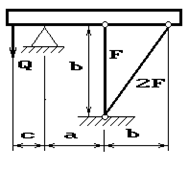
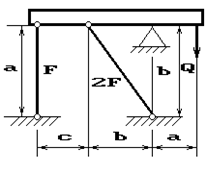
31 схема 32 схема 33 схема

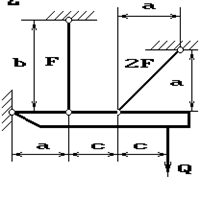
34 схема 35 схема 36 схема

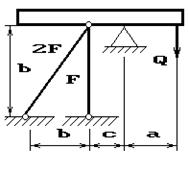
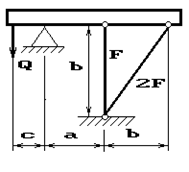
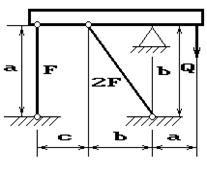
Рис.2

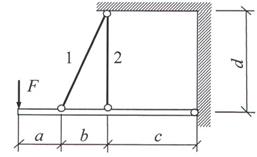
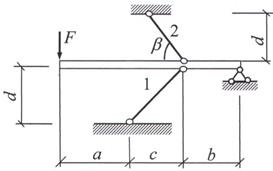
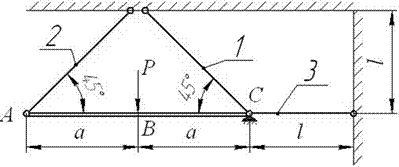
Задача 3. Статически неопределимые стержневые системы растяжения-сжатия. Расчет монтажных напряжений и температурных напряжений.

Жесткий брус, шарнирно закрепленный одним концом и подкрепленный двумя упругими стержнями, нагружен известной силой (рис. 3).

Для заданной конструкции требуется:

1) Вычертить ее схему в произвольном масштабе.

2) Рассчитать безопасные размеры стержней и подобрать в таблицах ГОСТа необходимые размеры равнополочных или неравнополочных уголков.

3) Рассчитать напряжения в стержнях, допустив, что один из них изготовлен на величину ∆ короче, то есть, найти монтажные напряжения.

4) Рассчитать напряжения в стержнях, возникающие от изменения температуры.

5) Найти суммарные напряжения в стержнях от внешней силы, от неточности монтажа, от изменения температуры.

6) Подсчитать недонапряжение или перенапряжение стержней.

Примечание: принять модуль Юнга Е = 2∙10⁵ МПа, коэффициент линейного расширения α=125∙10^-7 1/°С.

Данные взять из табл.3.

Таблица 3

Номер cтроки	Схема по рис.3	F, кН	а, м	b, м	∆, мм	∆t, °С	σadm, МПа
01	1	60	1,5	1,7	0,2	20	90
02	2	65	1,4	1,6	0,3	30	100
03	3	70	1,3	1,5	0,4	40	110
04	4	75	1,2	1,4	0,2	25	120
05	5	80	1,0	1,3	0,1	35	140
06	6	85	0,9	1,2	0,4	20	90
07	7	90	0,8	1,1	0,2	25	100
08	8	60	1,2	1,0	0,3	30	120
09	9	80	1,4	0,8	0,4	35	140
10	10	100	1,3	1,0	0,5	40	120
11	11	65	1,3	1,5	0,3	30	110
12	12	70	1,2	1,4	0,4	40	120
13	13	75	1,0	1,3	0,2	25	140
14	14	80	0,9	1,2	0,1	35	90
15	15	85	0,8	1,1	0,4	20	100
16	16	90	1,2	1,0	0,2	25	120
17	17	60	1,4	0,8	0,3	30	140
18	18	80	1,3	1,0	0,2	35	90
19	19	65	1,5	1,7	0,3	20	100
20	20	70	1,4	1,6	0,4	30	110
21	21	75	1,3	1,5	0,2	40	120
22	22	80	1,2	1,4	0,1	25	140
23	23	85	1,0	1,3	0,4	35	90
24	24	90	0,9	1,2	0,2	20	100
25	25	60	0,8	1,1	0,3	25	120
26	26	80	1,2	1,0	0,4	30	140
27	27	100	1,4	0,8	0,5	35	120
28	28	65	1,3	1,0	0,3	40	110
29	29	70	1,3	1,5	0,4	30	120
30	30	75	1,2	1,4	0,2	40	140
31	31	80	1,0	1,3	0,1	25	90
32	32	85	0,9	1,2	0,4	35	100
33	33	90	0,8	1,1	0,2	20	120
34	34	80	1,2	1,0	0,3	25	140
35	35	100	1,4	0,8	0,4	30	120
36	36	65	1,3	1,0	0,2	35	110
	г	в	а	б	г	а	б

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

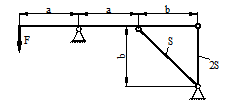
17 схема 18 схема

19 схема 20 схема

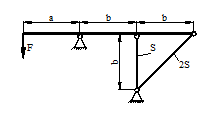
21 схема 22 схема

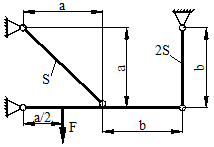
23 схема 24 схема

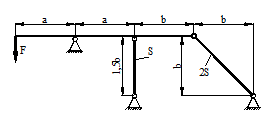
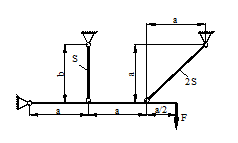
25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.3

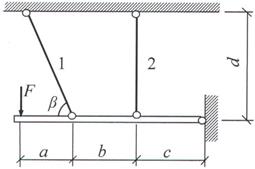
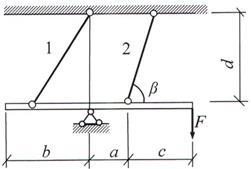
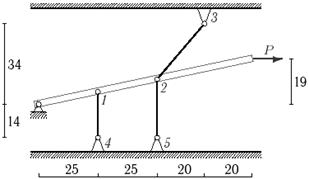
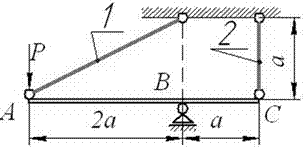
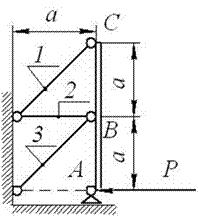
Задача 4. Статически неопределимые стержневые системы растяжения-сжатия.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и поддерживается двумя стержнями из пластичной стали (на рис.4).

Требуется:

1. Выполнить расчет системы по упругой стадии работы:

1.1) подобрать сечение стержней на действие заданной нагрузки;

1.2) определить в элементах системы температурные напряжения, вызванные изменением температуры стержня № 1;

1.3) вычислить начальные (монтажные) напряжения в стержнях, вследствие неточности изготовления стержня № 2

1.4) подсчитать суммарные напряжения в стержнях от совместного действия внешних факторов, перечисленных в пункте 1.1–1.3 и проверить их прочность.

2. Рассчитать заданную систему по методу предельного равновесия (по упругопластической стадии работы):

2.1) определить расчётную несущую способность системы при сечениях стержней принятых по пункту 1.1;

2.2) подобрать сечения стержней при заданной нагрузке.

3. Сравнить результаты расчёты системы по двум стадиям работы.

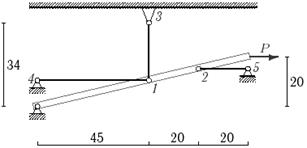
Данные плоской статически неопределимой системы (СНС), размеры ее элементов, соотношение площадей поперечного сечения стальных стержней, их физико-механические характеристики, изменение температуры одного из стержней и величину неточности изготовления другого стержня взять из табл. 4.

Для всех вариантов СНС принять модуль упругости стали Е = 2,06∙10⁵ МПа, коэффициент линейного расширения α= 1,25∙10^-5 °С^-1.

Таблица 4

Номер строки	Схема по рис.4	Нагрузка	Длины участков системы и стержней, м				Угол, град. β	Соотношение площадей сечений стержней А1/А2	Приращение температуры 1-го стержня ∆t, градус	Неточность изготовления 2-го стержня ∆0, мм	Расчетное сопротивление стержня, Мпа
		F, кН	а	b	c	d					№ 1	№ 2
											R1	R2
01	1	400	2	2,2	2,4	4,2	60	1,8	+40	-1,2	235	345
02	2	240	2,8	2	2,4	3,6	45	0,6	-60	+1,0	280	240
03	3	320	2,2	3,6	2,0	3,2	60	1,2	-30	+0,8	365	240
04	4	280	2,2	2,4	3,2	4,0	45	1,0	+45	-1,1	245	280
05	5	300	3,2	2,2	5,4	3,8	70	2,0	-35	-1,5	370	235
06	6	340	2,6	2,8	2,0	4,8	75	2,0	+40	+1,2	345	285
07	7	220	3,6	2,8	2,0	4,0	60	1,8	-50	+1,0	255	280
08	8	400	2,0	2,5	2,5	3,8	60	1,5	+30	-0,8	360	240
09	9	320	3,0	3,0	2,4	3,6	45	1,0	-40	-1,2	245	355
10	10	280	2,2	2,6	3.0	3,0	60	0,8	+35	-1,0	280	360
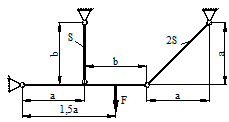
	е	в	г				д	б	е	г	д

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

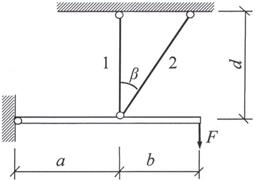
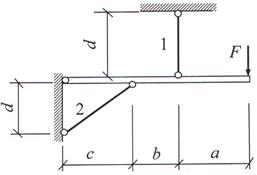
Рис. 4

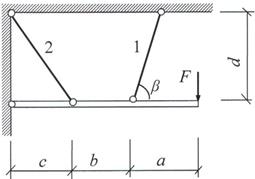
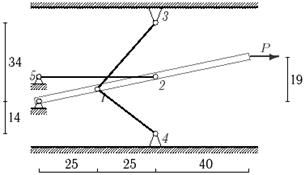
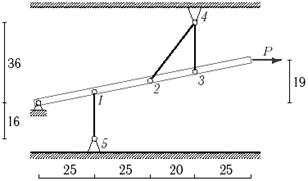
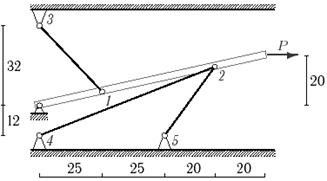
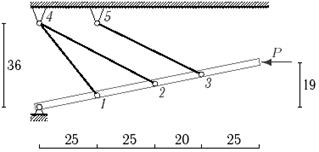
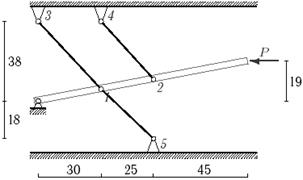
Задача 5. Статически неопределимые стержневые системы растяжения-сжатия.

Определить усилия в стержнях статически неопределимой стержневой системы (рис. 5).

Данные взять из табл.5.

Таблица 5

Номер cтроки	Схема по рис.5	P, кН
01	1	18
02	2	14
03	3	12
04	4	22
05	5	20
06	6	16
07	7	18
08	8	10
09	9	12
10	10	17
11	11	15
12	12	13
13	13	14
14	14	19
15	15	22
16	16	19
17	17	11
18	18	13
19	19	18
20	20	14
21	21	11
22	22	10
23	23	20
24	24	13
25	25	22
26	26	15
27	27	17
28	28	12
29	29	10
30	30	12
31	31	18
32	32	12
33	33	14
34	34	15
35	35	16
36	36	20
	б	в

1 схема 2 схема

3 схема 4 схема

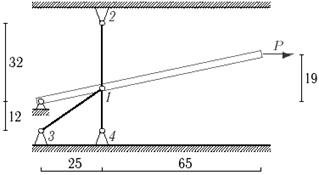
5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

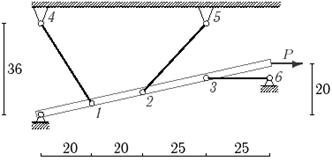
29 схема 30 схема

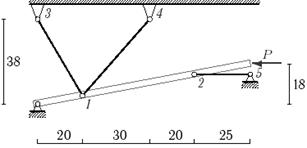
31 схема 32 схема

33 схема 34 схема

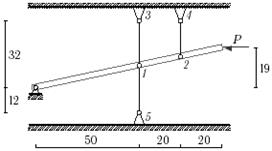
35 схема 36 схема

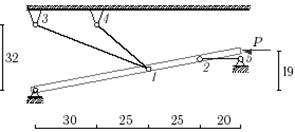
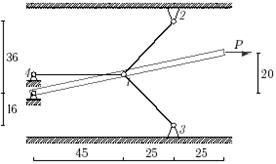
Рис.5

Задача 6. Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие

Исходные данные к задаче выбираются по табл. 6 и схемам на рис. 6.

Задача состоит из трех частей.

Часть 1. Определение грузоподъемности (или подбор сечения стержней) расчетом по упругой стадии деформации. Для этого:

1) нарисуйте в масштабе схему конструкции. При этом учитывайте, что отрицательные значения углов откладываются в сторону, противоположную показанной на рисунке;

2) нарисуйте план сил в недеформируемом состоянии и составьте необходимые уравнения статики;

3) изобразите план перемещений, соответствующий плану сил, и запишите уравнения совместности деформаций;

4) запишите физические уравнения, связывающие усилия и перемещения (закон Гука);

5) решив совместно уравнения равновесия, совместности деформаций и физические уравнения, найдите усилия в стержнях;

6) найдите напряжения в стержнях, выразив их через неизвестную нагрузку F (или площадь поперечного сечения A₁). Из условия прочности наиболее напряженного стержня определите допускаемую нагрузку (или подберите площадь поперечного сечения). Сосчитайте напряжения в стержнях при найденном значении F (или A₁).

Часть 2. Определение грузоподъемности (или подбор сечения стержней) расчетом по предельному пластическому состоянию. Для этого:

1) выявите, сколько стержней должно потечь, чтобы конструкция перешла в предельное состояние;

2) изобразите план сил в предельном состоянии, который должен соответствовать ранее построенному (в первой части задачи) плану перемещений;

3) составьте необходимые уравнения равновесия конструкции в предельном состоянии;

4) найдите предельную нагрузку. (Если неизвестными являются площади сечения стержней, выразите предельную нагрузку через площадь сечения какого-нибудь стержня);

5) из условия прочности всей конструкции определите грузоподъемность (или подберите сечения стержней);

6) сравните результаты расчетов по упругой стадии деформации и по предельному пластическому состоянию, подсчитав процент расхождения.

Часть 3. Определение дополнительных напряжений, вызванных изменением температуры одного из стержней ∆T_i (или неточностью изготовления ∆_i). Для этого:

1) изобразите в масштабе план перемещений, соответствующий заданному воздействию, и запишите уравнение совместности деформаций;

2) нарисуйте соответствующий плану перемещений план сил и составьте необходимые уравнения равновесия;

3) запишите физические уравнения;

4) решив совместно уравнения равновесия, совместности деформаций и физические уравнения, найдите усилия и напряжения в стержнях конструкции.

Таблица 6

Номер строки	F, кН	A1, см^2	∆i, мм	∆Ti, 0^С	i	β, град	Схема по рис. 6	A1/A2	a, м	l1, м	l2, м	b, м	α, град	Материал стержней
01	50	-	-	-40	1	90	1	0,4	2,0	3,0	4,0	4,0	0	Сталь
02	-	5	0,5	-	2	75	2	0,5	2,2	3,1	3,9	3,8	30	Бронза
03	100	-	-0,4	-	2	60	3	0,8	2,4	3,2	3,8	3,6	45	Дюралюминий
04	-	6	-	50	1	30	4	1,0	2,6	3,3	3,7	3,4	60	Сталь
05	150	-	-	60	2	15	5	1,2	2,8	3,4	3,6	3,2	-5	Бронза
06	-	7	-0,3	-	1	0	6	1,5	3,0	3,5	3,5	3,0	-60	Дюралюминий
07	200	-	0,2	-	1	15	7	1,8	3,2	3,6	3,4	2,8	-30	Сталь
08	-	8	-	-70	2	30	8	2,0	3,4	3,7	3,3	2,6	-15	Бронза
09	250	-	-	80	1	60	9	2,2	3,6	3,8	3,2	2,4	0	Дюралюминий
10	-	9	-0,1	-	2	90	10	2,4	4,0	4,0	3,0	2,2	15	Сталь
	г	а	в	б	г	а	в	б	г	а	в	б	г	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

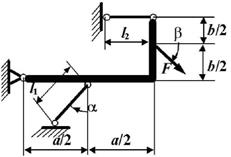
9 схема 10 схема

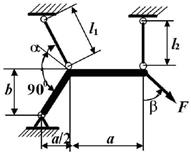
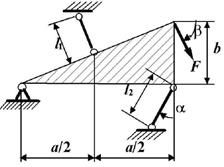
Рис. 6

Задача 7. Определение грузоподъемности статически неопределимой шарнирно-стержневой конструкции

Исходные данные к задаче выбираются по табл. 7 и схемам на рис. 7.

1.Определите грузоподъемность системы расчетом по упругой стадии деформаций. Для этого:

- постройте предполагаемые план сил и план перемещений, составьте соответствующие им уравнения равновесия и деформаций, запишите физические соотношения;

- решив полученную систему уравнений, определите усилия и напряжения в стержнях;

- из условия прочности наиболее напряженного стержня найдите допускаемую нагрузку.

2.Определите предельную грузоподъемность системы расчетом по упругопластической стадии. Для этого:

- считая напряжение в наиболее напряженном стержне (см. п. 1) равным пределу текучести, составьте уравнения равновесия узла, из которых определите усилия и напряжения в остальных стержнях. Выявите максимальные напряжения в упругих стержнях;

- определите предельную нагрузку на систему из условия равенства максимальных напряжений в упругих стержнях пределу текучести;

- найдите допускаемую нагрузку на конструкцию.

3.Определите предельную грузоподъемность системы расчетом по предельному пластическому состоянию. Для этого:

- выявите все кинематически возможные варианты предельного состояния конструкции;

- для каждого из возможных вариантов определите предельную нагрузку из условия предельного равновесия системы. Сопоставляя варианты, установите действительное предельное состояние;

- найдите допускаемую нагрузку и сравните ее с результатами, полученными в пп.1 и 2.

4*.Определите остаточные напряжения в стержнях системы при полной разгрузке из положения предельного равновесия.

Таблица 7

Номер строки	l1, м	α, град	A1, см^2	Схема по рис.7	l1, м	A2, см^2	β, град	γ, град	A3, см^2	Материал стержней
01	1,0	0	10	1	3,0	40	15	45	20	Сталь
02	1,5	15	20	2	2,5	30	30	60	30	Бронза
03	2,0	30	30	3	2,0	25	45	30	40	Дюралюмин.
04	2,5	0	40	4	1,5	15	60	15	25	Сталь
05	3,0	60	30	1	1,0	10	15	60	10	Бронза
06	2,5	45	20	2	1,5	20	30	45	15	Дюралюмин.
07	2,0	60	10	3	2,0	30	45	30	20	Сталь
08	1,5	15	15	4	2,5	40	60	30	30	Бронза
09	1,0	45	25	1	3,0	10	30	15	40	Дюралюмин.
10	2,0	30	40	2	1,0	20	45	60	10	Сталь
	в	б	а	г	в	б	а	г	в	б

1 схема 2 схема

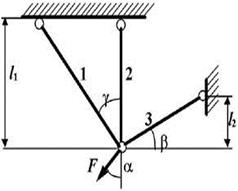
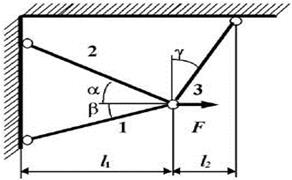
3 схема 4 схема

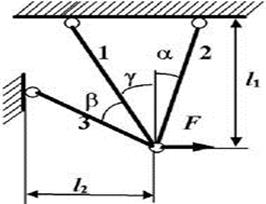
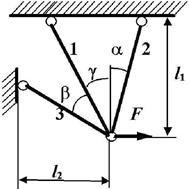
Рис. 7

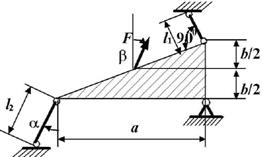
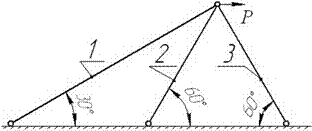
Задача 8. Подбор сечения статически неопределимой шарнирно-стержневой конструкции

Исходные данные к задаче выбираются по табл. 8 и схемам на рис. 8.

Абсолютно жесткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням.

Требуется подобрать сечения стержней по условию их прочности, приняв запас прочности по отношению к пределу текучести n_t=2,5.

Соотношение площадей поперечных сечений стержней указано на расчетных схемах, модуль упругости стали для всех вариантов E=2∙10⁵ Мпа.

Студенты строительных специальностей дополнительно определяют допускаемую силу, используя расчет по предельной грузоподъемности, и сравнивают ее с заданной.

Таблица 8

Номер cтроки	Схема по рис.8	P, кН	а, м	b, м	с, м	Марка стали	Предел текучести, МПа
01	1	11	2	2,1	2,4	20	250
02	2	12	2,1	2,2	2,2	30	300
03	3	13	2,2	2,3	2,5	40	340
04	4	14	2,4	2,4	2,7	20	250
05	5	15	2,6	2,5	2,5	50	380
06	6	16	2,8	2,6	2,1	30	300
07	7	17	2,8	2,7	2,5	40Х	800
08	8	18	2,7	2,8	2,9	20	250
09	9	19	2,9	2,9	2,0	40	340
10	10	20	2,4	3,0	2,6	40Х	800
11	1	11	2,6	2,5	2,1	20	250
12	2	12	2,8	2,6	2,2	30	300
13	3	13	2,8	2,7	2,3	40	340
14	4	14	2,7	2,8	2,4	20	250
15	5	15	2,9	2,9	2,5	50	380
16	6	16	2	3,0	2,6	30	300
17	7	17	2,1	2,1	2,7	40Х	800
18	8	18	2,2	2,2	2,8	20	250
19	9	19	2,4	2,3	2,9	40	340
20	10	20	2,6	2,4	3,0	40Х	800
21	1	11	2,8	2,5	2,1	20	250
22	2	12	2,8	2,4	2,2	30	300
23	3	13	2,7	2,6	2,3	40	340
24	4	14	2,9	2,8	2,4	20	250
25	5	15	2	2,8	2,5	50	380
26	6	16	2,1	2,7	2,6	30	300
27	7	17	2,2	2,9	2,7	40Х	800
28	8	18	2,4	2,0	2,8	20	250
29	9	19	2,6	2,2	2,9	40	340
30	10	20	2,8	2,3	3,0	40Х	800
31	1	15	2,8	2,4	2,2	20	250
32	2	16	2,7	2,5	2,3	30	300
33	3	17	2,9	2,6	2,4	40	340
34	4	18	2,2	2,8	2,5	20	250
35	5	19	2,4	2,9	2,6	50	380
36	6	20	2,6	3,0	2,7	30	300
	б	а	в	б	г	а	в

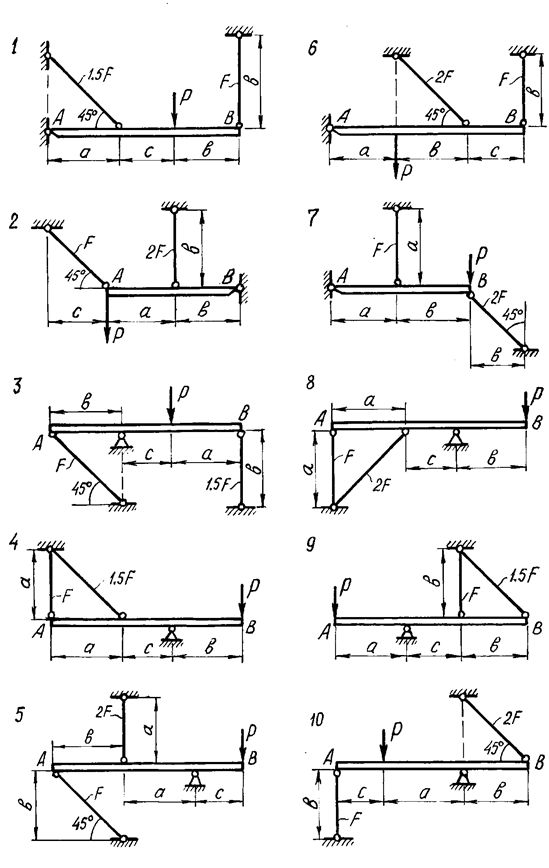
Рис.8

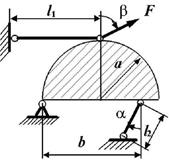
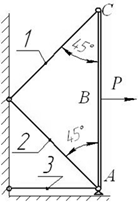
Задача 9. Определение допускаемого значения силы для статически неопределимой шарнирно-стержневой системы

Для заданной статически неопределимой системы (рис.9) определить допускаемое значение силы Р при допускаемом напряжении для стальных стержней [σ]=160 МПа.

Стержень АВС и плита схемы 9 – абсолютно жесткие.

Исходные данные к задаче выбираются по табл. 9 и схемам на рис. 9.

Таблица 9

Номер cтроки	Схема по рис.9	A1, см^2	A2, см^2	A3, см^2
01	1	5	2	2
02	2	4	3	6
03	3	3	4	3
04	4	2	5	5
05	5	6	6	2
06	6	3	2	5
07	7	5	3	4
08	8	2	4	3
09	9	5	5	2
10	10	4	6	6
11	1	3	2	3
12	2	2	3	5
13	3	6	4	2
14	4	3	5	5
15	5	5	6	4
16	6	2	2	3
17	7	5	3	2
18	8	4	4	6
19	9	3	5	3
20	10	2	6	5
21	1	6	2	2
22	2	3	3	5
23	3	5	4	4
24	4	2	5	3
25	5	5	6	2
26	6	4	2	6
27	7	3	3	3
28	8	2	4	5
29	9	6	5	2
30	10	3	6	5
31	1	5	2	4
32	2	2	3	3
33	3	5	4	2
34	4	4	5	6
35	5	3	6	3
36	6	2	2	5
	б	а	в	б

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

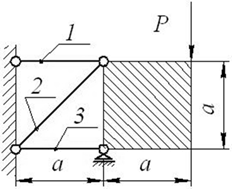
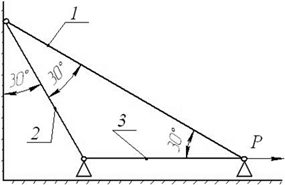
Рис.9

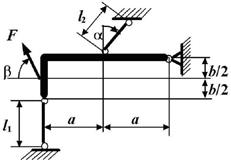
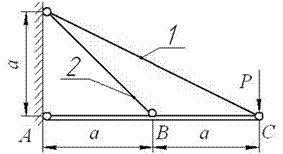
Задача 10. Построение эпюр нормальных усилий в стержнях статически неопределимой шарнирно-стержневой системы

Для статически неопределимой шарнирно-стержневой системы, содержащей деформируемые стержни и абсолютно жесткие элементы (рис. 10) построить эпюру нормальных сил в деформируемых стержнях.

Исходные данные к задаче выбираются по табл. 10 и схемам на рис. 10.

Таблица 10

Номер cтроки	Схема по рис.10	F/P
01	I	2
02	II	–1
03	III	2
04	IV	1
05	V	–2
06	VI	1
07	VII	2
08	VIII	–1
09	IX	–2
10	I	–3
11	II	2
12	III	–1
13	IV	2
14	V	1
15	VI	–2
16	VII	1
17	VIII	2
18	IX	–1
19	I	–2
20	II	–3
21	III	2
22	IV	–1
23	V	2
24	VI	1
25	VII	–2
26	VIII	1
27	IX	2
28	I	–1
29	II	–2
30	III	–3
31	IV	2
32	V	–1
33	VI	2
34	VII	1
35	VIII	–2
36	IX	1
	в	б

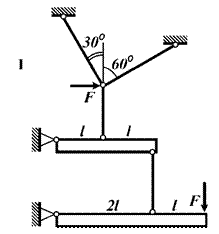
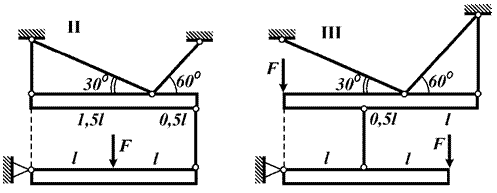
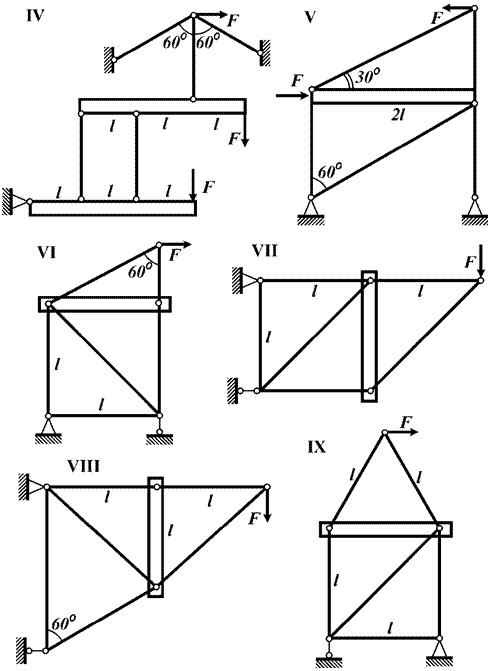
Рис.10

Примеры выполнения задач

Пример 1

Жесткий брус АВ закреплен, как показано на рис.11, и нагружен силой P.

Требуется подобрать сечения стержней из условия их прочности.

Дано: P= 5 кН; а =1,2 м; в =1,4 м; с =1,0 м; материал - сталь 40, σ_Т=340 Мпа, n_T=2,5; E=2∙10⁵ Мпа.

Рис.11. Расчетная схема

Решение.

Жесткий брус АВ закреплен с помощью шарнирно-неподвижной опоры и поддерживается двумя деформируемыми стальными стержнями АЕ и ВК. На опоре С (рис.11) - две составляющие реакции X_C и Y_C , реакции в стержнях направлены вдоль их осей и приложены к брусу АВ в точках А и В. Направление этих реакций рекомендуется установить после анализа возможного деформированного состояния конструкции.

Для плоской системы сил в общем случае ее приложения к конструкции можно составить только три независимых уравнения равновесия. В рассматриваемой задаче к брусу АВ приложено четыре неизвестных усилия: две реакции в шарнире и два усилия в стержнях. Разность между числом неизвестных усилий и числом уравнений статики показывает, что для определения этих неизвестных необходимо составить еще одно уравнение статики, в которое входили бы интересующие нас величины. Такое уравнение или несколько подобных уравнений можно получить из геометрических зависимостей между деформациями элементов заданной конструкции.

Рассмотрим конструкцию после деформации ее элементов (рис.12). Под действием силы Р жесткий брус может повернуться вокруг точки С, при этом стержни АЕ и ВК будут деформированы. Точки А и В описывают при повороте бруса дуги окружностей, которые ввиду малости перемещений заменяются касательными, т.е. считается, что эти точки перемещаются по перпендикулярам к радиусам АС и ВС этих дуг. Точка А смещается вниз и занимает положение A₁, точка В - вверх, занимая положение B₁. Брус, как абсолютно жесткий элемент конструкции, - положение A₁B₁. Очевидно, что стержень АЕ сжат и стал короче на величину AA₁=∆l₁. Соединив точки К и B₁, находим на чертеже положение стержня ВК после его деформации. Опустив перпендикуляр из точки В на прямую B₁K, находим точку B₂.

Рис. 12. Схема конструкции после деформации ее элементов

Отрезок B₁B₂=∆l₂ - удлинение стержня ВК.

Действительно, ∆l₂=KB₁-KB=KB₁-KB₂, так как КВ=КВ₂, и стержень КВ растянут.

Выяснив направление усилий в стержнях, показываем векторы этих усилий на схеме недеформированного состояния конструкции (см. рис. 11) и составляем уравнение ее равновесия:

ΣM_C=0: -N₁∙(c+a)+P∙a-N₂sin45⁰∙b=0 (1)

Определения составляющих реакции шарнира X_C , Y_C для решения данной задачи не требуется, и два других уравнения статики не составляются.

Для вычисления усилий в стержнях N₁, N₂ необходимо иметь еще одно уравнение, называемое уравнением совместности деформаций. Это уравнение получаем из геометрических соотношений между деформациями элементов заданной конструкции. При этом ввиду малости деформаций изменением угла наклона стержня ВК пренебрегаем, считая что ∠BB₁B₂=45⁰.

Тогда

Из подобия треугольников A₁AC и B₁BC находим соотношение между деформациями стержней - ∆l₁ и ∆l₂:

Полученная зависимость (2) называется условием совместности деформаций.

Абсолютные удлинения стержней можно выразить через усилия, используя формулу Гука:

Подставив выражения (3) в условие совместности деформаций (2), получим

Решая систему уравнений (1) и (4), определяем усилия в стержнях N₁, N₂. Для этого подставим значение N₁ из (4) в уравнение (2):

-2,4N₂∙(c+a)+Pa-N₂sin45⁰∙b=0;

-2,4N₂∙(1+1,2)+5∙12-N₂sin45^0∙1,4=0.

Решив систему уравнений, получим

N₂=0,96 кН;

N₁=2,4∙0,96 = 2,3 кН.

Определив усилия в стержнях, переходим к подбору площадей их поперечных сечений.

Для заданного материала вычислим допускаемое напряжение

Определяем напряжения в стержнях и выбираем большее:

Площадь сечения F подбираем по условию прочности наиболее нагруженного стержня. Так как σ₁ больше σ₂, используем условие прочности первого стержня:

F≥0,17∙10^-4 м²=0,17 см².

Площади сечений стержней принимаем в соответствии с заданным соотношением:

F₁=F=0,17 см²; F₂=1,3F=1,3∙0,17=0,221 см².

Определение допускаемой силы Р по условию задачи производится по предельной грузоподъемности конструкции.

Предельным состоянием конструкции называется такое состояние, при котором она начинает деформироваться без увеличения нагрузки.

В данном примере это произойдет в том случае, когда напряжения во всех стержнях достигнут предела текучести

σ₁=σ₂=σ_T.

Усилия в стержнях будут определяться по формулам

N₁=σ_T∙F₁; N₂=σ_T∙F₂. (5)

Нагрузка, соответствующая предельному состоянию, называется предельной. Ее величину можно найти из уравнения предельного равновесия, которое получается из уравнения (1) после подстановки в него значений N₁, N₂:

-σ_T∙F₁∙(c+a)+P_пр∙a-σ_T∙F₂∙sin45⁰∙b=0.

P_пр=[σ_T∙F₁∙(c+a)+σ_T∙F₂∙sin45⁰∙b]=[340∙10⁶∙0,17∙10^-4∙(1+1,2)+340∙10⁶∙0,221∙10^-4∙sin45⁰∙1,4]=16,8∙10³ Н.

Допускаемая нагрузка с учетом заданного коэффициента запаса

Величина допускаемой нагрузки при расчете по предельной грузоподъемности получается большей, чем при расчете по допускаемым напряжениям:

Разница составляет 34%, что является результатом разных предположений об опасном состоянии конструкции: при расчете по допускаемым напряжениям опасным считается состояние, при котором только в одном стержне напряжение достигает предела текучести. Для статически неопределимых систем расчет по предельной грузоподъемности дает более экономичное решение при назначении размеров сечения, и им широко пользуются в строительной практике.

Пример 2

Расчет статически неопределимой конструкции.

Для заданной статически неопределимой стержневой системы (рис. 13,а) требуется:

1) определить усилия и напряжения в поперечных сечениях стержней, выразив их через q, при этом горизонтальный брус, подвешенный на стержнях, считать абсолютно жестким;

2) из условия прочности стержней определить допускаемое значение [q], если предел текучести σ_т = 240 МПа, коэффициент запаса прочности к_т = 1,5, а = 2,5 м, А = 350 мм².

Рис.13

Решение.

1) Определение усилий и напряжений в стержнях.

Из расчетной схемы стержневой системы следует, что при нагружении абсолютно жесткого бруса ДС, равномерно – распределенной нагрузкой q в стержнях 1, 2, 3, которые имеют шарнирные крепления, по концам возникнут осевые усилия N₁, N₂, N₃ растяжения или сжатия. Найдем усилия в стержнях. Конструкция один раз статически неопределима, так как имеет одну лишнюю связь.

1. Статическая сторона задачи.

Мысленно разрезаем каждый стержень поперечным сечением (рис. 13, б) и заменяем действие отброшенной верхней части продольными силами N₁, N₂, N₃ (силы направляем от сечения, т.е. считаем их положительными, а стержни работающими на растяжение). Условия равновесия балки, а в данном случае системы параллельных сил (N₁, N₂, N₃ и q) будут

ΣF_iy = N₁ + N₂ + N₃ - q·2а = 0; (1)

ΣМ_Д(F_i) = N₂·2а + N₃· 3а – q ·2а· а = 0 (2)

так как в качестве центра момента выбрана точка Д, через которую проходим линия действия силы N₁, то в уравнении (2) неизвестных будет меньше.

Оставив в левой части в качестве неизвестных N₁, N₂, N₃, уравнения (1) и (2) приведем к виду:

N₁ + N₂ + N₃ = 2qа (3)

2·N₂ + 3 ·N₃ = 2qа

Получили систему двух уравнений с тремя неизвестными, которая методами статики не решается.

2. Геометрическая сторона задачи.

Рассматривая систему в деформированном состоянии, устанавливаем связи между деформациями стержней 1, 2, 3. Полученное уравнение называем уравнением совместности деформаций. Уравнение в деформациях составляем из предположения, что балка как жесткое целое переместится вниз и повернется относительно почки Д (рис. 13, в). Тогда из подобия треугольников В₁В₂Д₁ и С₂С₁Д₁ следует,

Из пропорции получаем 3·(∆l₂ - ∆l₁) = 2·(∆l₃ - ∆l₁), приведя подобные члены, имеем ∆l₁ - 3∆l₂ + 2∆l₃ = 0 (4)

Уравнение (4) представляет собой уравнение совместности деформаций.

3. Физическая сторона задачи.

На основании закона Гука выражаем деформации стержней через действующие в них неизвестные усилия. По закону Гука

Поэтому

т.к. l₁=l₂=2l; l₃=l; Е₁=Е₂=Е₃=Е; А₁=А₂=А; А₃=2А, то подставив соотношения (5) в уравнение (4), получим

или 2N₁ - 6N₂ + N₃ = 0 (6)

Синтез.

Решая совместно статические, геометрические и физические уравнения, находим неизвестные усилия.

Присоединяем уравнение (6) к уравнению (3) получим систему уравнений

N₁ + N₂ + N₃ = 2·qа

2N₂ + 3N₃ = 2·qа (7)

2N₁ - 6N₂ + N₃ = 0

Рассмотрим уравнение (1) и (3) этой системы

N₁ + N₂ + N₃ = 2 qа

2 N₁ - 6 N₂ + N₃ = 0

Умножим первое уравнение на 2 и вычтем из него 2^ое уравнение, получим:

8N₂ + N₃ = 4·qа (8)

Полученное уравнение рассмотрим с уравнением (2) системы (7)

8N₂ + N₃ = 4·qа

2N₂ + 3N₃ = 2·qа ×4

Умножим второе уравнение на 4 и вычтем из первого второе, получим

-11∙N₃ =-4qа N₃=4qa/11;

Подставив N₃ в уравнение (8), получим:

8N₂+4qa/11=4qa

8N₂=4qa-4qa/11=40qa/11;

Подставив N₃ и N₂ в первое уравнение системы (7), определим N₁

Замечание.

Выбор схемы деформированной стержневой конструкции при моделировании нагружения не имеет принципиального значения.

Определяем напряжение в стержнях конструкции

2) Определение допускаемого значения нагрузки [q].

Определяем допускаемое напряжение по заданному пределу текучести и коэффициенту запаса прочности

Из условия прочности при растяжении или сжатии максимальное напряжение не должно превышать допускаемого, т.е. σ_max≤[σ].

Из полученных значений напряжений в пункте (2), видно, что

поэтому

Ответ: [q] = 19 Н/мм = 0,019 Н/м.

Пример 3.

Три стержня, шарнирно скрепленные в одной точке (рис. 14), имеют одинаковые поперечные сечения. Определить площадь поперечного сечения, принимаем [σ] = 160 МПа, F = 120 кН.

Рис.14

Решение.

Из расчетной схемы конструкции, в которой стержни в узлах закреплены шарнирно и нагружены в узле С силой F, следует, что в стержнях будут возникать только осевые усилия. Определение площади поперечного сечения при растяжении или сжатии (проектный расчет) выполняют по условию прочности

откуда, если известно усилие N, определяют необходимую площадь

Найдем усилия в стержнях конструкции.

1. Статическая сторона задачи.

Вырезаем узел С (рис. 14,б) и составляем два уравнения равновесия действующих на него сил, как для плоских систем сходящихся сил, предполагая, что стержень 1 – растянут, а стержни 2 и 3 – сжаты:

ΣF_ix = N₂ ·sinα – N₃ ·sinα = 0 (1)

ΣF_iy = N₁ + N₂·cosα + N₃·cosα = 0 (2)

из уравнения (1), получаем N₂ = N₃.

В результате остается одно второе уравнение, содержащее два неизвестных усилия:

N₁ + 2·N₂·cosα = F (3)

Получим на основе уравнений статики одно уравнение с двумя неизвестными, поэтому система один раз статически неопределима.

2. Геометрическая сторона задачи.

Так как система симметрична относительно оси первого стержня и боковые стержни сжимаются одинаковыми силами, то под действием силы F узел С при деформации стержней опустится по вертикали на величину ∆l₁. Все стержни деформируются и займут положение, показанные на (рис.14,в) штриховыми линиями. Укорочения боковых стержней получим, если из точек Д и В радиусом, равным ДС или ВС, проведем дуги через точки С₁ и сделаем засечки на длинах ДС и ВС. Ввиду малости деформаций можно считать, что углы между осями стержней не изменяются, а проведенные дуги заменяются перпендикулярами. Из прямоугольного треугольника СКС₁, имеем:

или
3. Физическая сторона задачи. Удлинение стержней выразим по закону Гука через действующие усилия:

, так как А₁ =А₂ =А,

Синтез. Подставляя ∆l₂ и ∆l₁ в уравнение (4) получим

или N₂=N₁∙cosα (5)

Присоединив уравнение (5) к уравнению (3), получим систему уравнений

N₁ + 2·N₂ ·cosα = F (6)

N₁·cosα - N₂ = 0

Подставим N₂ = N₁·сosα в первое уравнение системы (6)

N₁ + 2·N₁·сos²α = F

отсюда

N₂=N₁cosα=48000∙=41616 Н.

Так как площади стержней одинаковы, то максимальное напряжение возникает в первом стержне

отсюда

Итак А = 3 см².

Пример 4

Определить усилия в упругих стержнях (в функции угла α), имеющих одинаковую жесткость на растяжение EA, длину l и удерживающих невесомый абсолютно жесткий брус AB, нагруженный силой F (рис. 15, а).

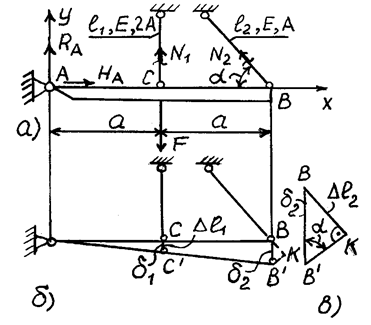
Рис.15

Решение.

1. Вводят внутренние усилия N₁ и N₂ и составляют условия статического равновесия:

Σm_A=0; N₁a-Fa+N₂sinα∙2a=0. (1)

Возможно составление еще двух уравнений равновесия: Σx=0; Σy=0. Но они не нужны для решения вопроса, поставленного в задаче. В итоге имеются четыре неизвестных (R_A, H_A, N₁, N₂) и три уравнения равновесия. Задача один раз статически неопределима.

2. Представляют систему в деформированном виде (рис. 15, б). Шарниры C и B переместятся в положение C’ и B’ относительно шарнира A.

Используя принцип начальных размеров, можно считать, что перемещения δ₁ и δ₂ происходят перпендикулярно брусу AB. Из подобия треугольников ACC’ и ABB’ получают:

(2)

(3)

Из рис. 15, б следует: δ₁=∆l₁. (4)

На рис. 15, в показан в увеличенном виде ∆BB’K, из которого следует

(5)

Подставив формулы (4) и (5) в (3), получают

(6)

Используя закон Гука, записывают (3) в виде:

Отсюда N₁=N₂/sinα. (8)

Подставив (8) в (1), находят значение N₂, а затем, подставив полученную величину в (8), вычисляют значение N₁.

Анализируя формулы (8) и (7), можно сделать выводы:

а) усилия в статически неопределимых системах зависят на только от величины внешних нагрузок и геометрических величин, характеризующих форму и размеры конструкции, но и от соотношения жесткостей сечений EA ее элементов или, если материал последних одинаков, от соотношения площадей их сечений, тогда как в статически определимых системах усилия зависят лишь только от нагрузок и геометрических характеристик – формы и размеров конструкции;

б) для статически неопределимой системы в общем случае нельзя добиться равенства напряжений во всех элементах и, следовательно, требование обеспечить в каждом из них напряжения, равные допускаемым, неосуществимо.

Пример 5

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 16).

Дано: A=12 см², a=2,4 м, b=2,2 м, с=1,5 м.

Требуется:

1) найти усилия и напряжения в стержнях, выразив их через силу Q;

2) найти допускаемую нагрузку Q_доп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ]=160 МПа;

3) определить перемещение точки приложения силы Q;

4) найти предельную грузоподъемность системы и допускаемую нагрузку Q_доп, если предел текучести σ_m=240 Мпа и запас прочности k=1,5;

5) сравнить величины Q_доп, полученные при расчете по допускаемым напряжениям (см. п. 2) и допускаемым нагрузкам (см. п. 4).

Рис. 16

Решение.

Данная система статически неопределима один раз, поскольку четыре неизвестных (N₁, N₂, H_k, R_k) не могут быть определены из трех независимых уравнений равновесия. Поэтому кроме статической стороны задачи необходимо рассмотреть геометрическую и физическую стороны задачи.

Рис. 17

Рассмотрение статической стороны задачи (рис. 17) дает следующее уравнение равновесия:

ΣM_k=0, N₁∙2,2+N₂∙sin45°∙2,4-Q∙3,7=0, sin45°=0,707.

Из геометрической стороны задачи (рис. 16) следует:

где δ₁, δ₂ – перемещения точек прикрепления стержней 1 и 2 к жесткому брусу; δ_Q – перемещение точки приложения силы Q; ∆l₁, ∆l₂ – деформации стержней 1 и 2.

Выразить деформации стержней ∆l₁ и ∆l₂ через усилия N₁ и N₂ помогает физическая сторона задачи (по закону Гука – ):

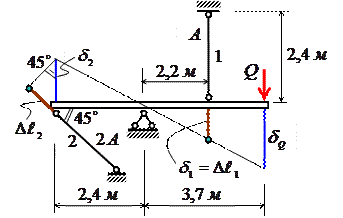
Рис. 18

Решая совместно систему полученных уравнений, определим значения N₁ и N₂ в долях от Q:

Напряжения в поперечных сечениях стержней 1 и 2 будут равны:

Допускаемую нагрузку находим из условия прочности по нормальным напряжениям, приравняв большее из напряжений в двух стержнях допускаемому напряжению:

Рис. 19

Перемещение точки приложения силы Q согласно рис. 19 будет равно:

Предельную грузоподъемность системы найдем, подставив в уравнение равновесия (рис. 17) предельные значения усилий в стержнях:

ΣM_k=0, σ_m∙A∙2,2+σ_m∙2A∙sinα∙2,4-∙3,7=0, =435,4 кН.

Допускаемая нагрузка Q_доп будет равна

Сравнивая величины Q_доп, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам, получаем Q_доп больше при расчете по допускаемым нагрузкам в раза.

Пример 6

Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис.20).

Дано:

Требуется:

1. Установить степень статической неопределимости.

2. Найти усилия и напряжений в стержнях, выразив их через силу

3. Найти допускаемую нагрузку

4. Найти предельную грузоподъемность

5. Найти допускаемую нагрузку

6. Сравнить значения допускаемой нагрузки, найденные в п. 3 и в п. 5.

Рис.20

Решение.

1. Система один раз статически неопределима, так как для определения четырех неизвестных усилий () имеем три независимых уравнения статики.

2. Найдем усилия в стержнях

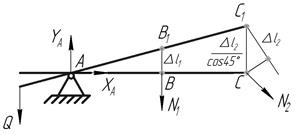
Рис.21

Для раскрытия статической неопределимости найдем условие совместности деформаций (рис.21). Из подобия треугольников и :

Запишем соотношения закона Гука между деформациями и усилиями:

Подставляя (3) в (2) окончательно получим:

(1) и (4) образуют замкнутую систему для нахождения и . Из решения полученной систему находим:

Напряжения в стержнях:

3. Найдем допускаемую нагрузку

4. Найдем предельную грузоподъемность

Предельные значения усилий в стержнях: Воспользуемся уравнением равновесия (1):

5. Найдем допускаемую нагрузку

6. Сравниваем значения допускаемой нагрузки, найденные при расчете по допускаемым напряжениям и допускаемым нагрузкам:

следовательно, расчет по предельному состоянию более экономичен.

Пример 7

Стержневая система, состоящая из абсолютно жесткой балки АВ и поддерживающих ее стальных стержней №1 и №2 (рис.22), имеющих длины , находится в равновесии под действием заданной нагрузки P.

Дано:

Модуль упругости, коэффициент линейного расширения, предел текучести материала стержней принять соответственно: Собственный вес балки АВ не учитывать.

Условия устойчивости сжатых стержней считать выполненными.

Требуется:

1. Определить усилие в стержнях от действия силы P, если отношение площадей поперечных сечений стержней задано: ;

2. Подобрать площади сечений стержней по условиям прочности;

3. После подбора сечений, проверить напряжение в стержнях;

4. Определить усилия в стержнях при и сделать вывод.

Примечание: при выполнении п.2 задания, следует пользоваться методом допускаемых напряжений, приняв

где n – коэффициент запаса прочности.

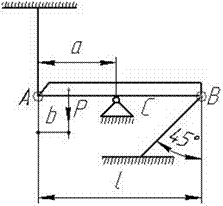
Рис.22

Решение:

1. Для определения усилий в стержнях 1 и 2 применяют метод сечений. Стержни 1 и 2 мысленно разрезаем плоскостью перпендикулярной оси стержня, отбрасываем верхнюю часть, а в местах разреза прикладываем неизвестные внутренние усилия N₁ и N₂ (рис.23).

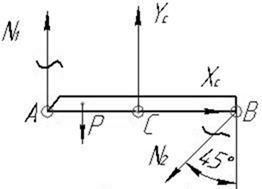
Рис.23

Составляем уравнение равновесия статики для балки АВ, таким является уравнение в виде суммы моментов всех сил относительно шарнира C:

Получили одно уравнение равновесия с двумя неизвестными N₁ и N₂. Два других уравнения: сумма сил относительно осей применять не целесообразно, так как в них войдут две неизвестные реакции в шарнире C. Таким образом, задача является один раз статически неопределимой, то есть не может быть решена с помощью только одних уравнений равновесия. Поэтому необходимо рассмотреть деформации стержней, то есть составить уравнение совместности деформаций.

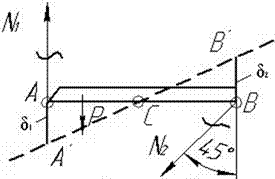
Рис.24

На рис.24 показана штриховой линией ось бруса после деформации системы. Эта ось остается прямолинейной, так как балка по условию задачи является абсолютно жесткой и, следовательно, не деформируется, а может лишь повернуться вокруг точки C. Шарниры A и B после деформации переходят в положения A^’ и B^’ соответственно, т.е. перемещаются по вертикали на величины . Из подобия треугольников AA^’C и BB^’C находим:

Выразим удлинение стержня AA^’ и удлинение стержня BB^’ через перемещения . Для этого спроектируем перемещения на направления стержней: Откуда:

По закону Гука:

По условию

Полученное выражение подставим в уравнение равновесия статики для балки АВ:

При имеем

Оба стержня сжаты.

Найденные значения проверим по уравнению равновесия статики для балки АВ:

2. Расчет прочности выполняется с использованием условий прочности. Условие прочности конструкции записывается в виде:

откуда

При этом должно быть ;

Так как , а , то и F1 принимаем равной

3. Проверим напряжение в стержнях.

откуда

4. Зависимость между P, k, N₁ и N₂:

При получим

.

Из этой зависимости следует, что с увеличением отношения т.е. при увеличении жесткости второго стержня, усилие в стержне N₂ возрастает, а в стержне N₁ – уменьшается: происходит перераспределение нагрузки.

Пример 8

Стержневая система, состоящая из трех деформируемых стержней, находится в равновесии под действием заданной нагрузки P (рис.25).

Дано: l₁ = 5,5 м, l₃ = 4,5 м, Р = 70 кН, = = 45°, F₁/F₂ = 0,8.

Требуется: определить опорные реакции в стержнях AC и BC.

Рис.25

Решение.

Изобразим на схеме предполагаемые направления реакций. В системе возникает четыре реакций, а уравнений статики для плоской системы можно составить лишь три, следовательно, система один раз статически неопределима (n = 4 – 3 = 1). Таким образом, помимо уравнений статики потребуется составить еще одно уравнения совместности деформаций. Поскольку в конечном итоге требуется определить величины усилий в стержнях 1 и 4, то записав в качестве уравнения сумму моментов всех сил относительно точки К, можно исключить из последующего рассмотрения реакций R_К и .

Уравнение равновесия:

- P∙l₃ + 2R_A∙l₃ + 2l₃∙R_B∙cosα= 0;

Для составления уравнения совместимости деформаций определим сначала длину стержня 4. Рассмотрим треугольник ∆АВС, так как угол С = 45° то и угол В = 45°, следовательно ∆АВС равнобедренный. Отсюда по теореме Пифагора определим длину стержня 4:

где АС = АВ = 5,5 м.

Теперь, рассматривая систему видим, что под действием силы Р стержни l₁ и l₄ деформируются (сжатие). Сделаем допущение. Пусть точка С остается на линии стержня l₁, а угол α остается не низменным так как его изменения незначительны. Из выше изложенного изобразим рис.26.

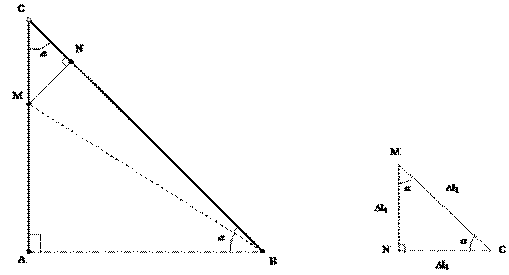
Рис.26

Рассматривая два треугольника ∆АВС и ∆МNС делаем вывод, что они подобны. Отсюда по правилу подобия составим пропорцию:

∆l₁ = MC, ∆l₄ = NC = MN.

– уравнение совместности деформаций

Получив уравнение совместности деформаций и одно уравнение статики, можно решить систему двух уравнений с двумя неизвестными и найти величины R_A и R_B.

Для этого воспользуемся законом Гука для i–го стержня:

,

тогда

Подставляем это выражение в уравнения статики:

; -P∙l₃ + 2R_A∙l₃ + 2l₃∙R_B ∙cosα= 0;

-P∙l₃ + 2·(1,4·)∙l₃ + 2l₃∙R_B ∙cosα= 0;

-70· 4,5 + 2·(1, 4·)·l₃ + 2·4,5·R_B·0,7 = 0;

-315 + 10,2·R_B + 6,3·R_B = 0;

-315 + 16,5·R_B = 0;

тогда

Ответ: R_B = 19 кН, R_A = 21 кН.

Пример 9

На рис.27 изображена абсолютно жесткая балка ВС, нагруженная посередине силой Р. Балка удерживается в горизонтальном положении шарнирно – подвижной опорой С и тремя стальными стержнями. Заданы площади сечений стержней А₁ = 4 см²; А₂ = 3 см²; А₃ = 2 см². Определить допускаемое значение силы Р , если допускаемое напряжение для материала стержней, равное [σ] = 160 МПа, одинаково при растяжении и сжатии.

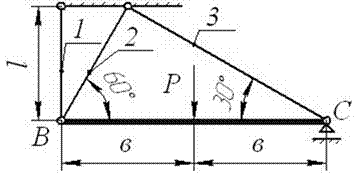
Рис.27

Решение.

Допускаемая нагрузка (сила Р) определяется по условию прочности наиболее напряженного стержня. Полагая значение силы Р известным, найдем напряжения в сечениях стержней системы, выразив их через силу Р.

Мысленно рассекаем стержни и, полагая стержни растянутыми, изображаем силы, приложенные к отсеченной части (рис.28).

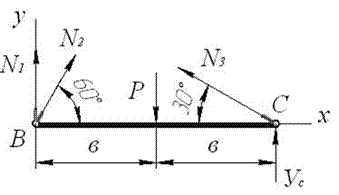
Рис.28

Уравнения равновесия

Система (1) содержит 4 неизвестных величины: N₁, N₂, N₃ и Y_c. Лишь второе уравнение содержит реакцию опоры С, величина которой не влияет на значение допускаемой нагрузки, а потому ограничимся первым и третьим уравнениями. Двух уравнений системы (1) недостаточно для определения трех продольных сил. Необходимо дополнить их уравнением совместности деформаций.

По условию задачи брус ВС является абсолютно жестким. Значит, перемещение системы осуществляется лишь за счет деформации стержней. Опора С допускает только горизонтальное смещение узла С. Такое же горизонтальное смещение получает и узел В. Эти перемещения изображены на рисунке 29.

Следует учесть, что истинные перемещения точек В и С в сотни раз меньше размеров бруса ВС. Поэтому перемещения точек стержней при их поворотах изображены не дугами окружностей, а прямыми отрезками, перпендикулярными стержням. Заметим, что стержень 3 по предположению растянут, но на рисунке изображено его укорочение, значит изображенная деформация его не ∆l₃, а -∆l₃.

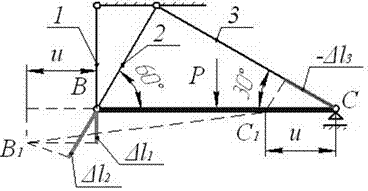
Рис.29

По рис.29

При u= -∆l₃/cos30° получаем геометрическую связь деформаций

В соответствии с законом Гука

Подстановкой выражений (3) в равенство (2) получим уравнение, дополняющее систему (1).

После подстановки значений А₁, А₂, А₃ и упрощения уравнений (1) и (4) получим систему

N₂-1,732N₃=0;

N₁+0,866N₂=0,5P; (5)

9N₁-16N₂-24N₃=0.

Решение уравнений (5)

N₁=0,396P, N₂=0,119P, N₃=0,069P.

При заданных сечениях стержней

Наибольшее напряжение σ_max=σ₁=0,0991P.

По условию прочности σ_max≤[σ] допускаемая нагрузка

Пример 10

Стержневая система, состоящая из жесткого стержня АЕ и двух других стержней ВС и ВК, нагружена силой Р=35 кН (рис. 30). Определить коэффициент запаса прочности стержневой системы, если =45⁰, l₁=0,6 м, l₂=0,3 м, l₃=0,6 м, А=800 мм², k=1,2, материал – сталь 30Х с пределом текучести =845,7 МПа.

При известной площади сечения выполняется проверочный расчет на прочность по напряжениям. Величина фактического коэффициента запаса , где – предельное значение напряжения для заданного материала. – максимальное рабочее напряжение, возникающее в заданной стержневой системе от приложенных нагрузок. Сталь 30Х пластичный материал, тогда , следовательно .

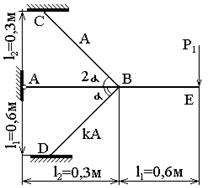
Рис.30

Решение.

1) Уравнения равновесия.

Составим уравнения статического равновесия (рис. 31):

; (1)

; (2)

; (3)

Рис.31

Для дальнейшего решения применяем уравнение (3), так как реакции заделки А для оценки прочности не нужны. Преобразуем (3), подставляя значения углов и длин, получим

Полученное уравнение содержит две неизвестные величины N_CB и N_DB.Сопоставляем дополнительное уравнение, которое вытекает из условия совместности перемещений.

2) Уравнения совместности деформаций.

Составим уравнения совместимости деформаций (рис. 32): l_CB=B’B’₁; l_DB=B’B’₂. Из DBB’B’₁ имеем BB’=B’B’₁/sin2; из BB’B’₂ получим BB’=B’B’₂/sin, приравняем отрезки

подставляя данные углы, получим

l_DB=0,7l_CB (5).

Рис.32

3) Физические уравнения.

Составим физические уравнения. По закону Гука

Подставляя в уравнение совместности перемещений, с учетом длин стержней, соотношений площадей и материала, получим

умножим на ЕА и подставим данные

после вычислений получим

4) Расчет усилий в стержнях.

Статическое уравнение (4) и дополнительно преобразованное уравнение (6) совместности перемещений дают систему разрешающих уравнений:

Из решения системы уравнений получим N_DB=1,11P; N_CB=3,77P.

5) Расчет на прочность.

Напряжения в стержнях

Видно, что максимальные напряжения возникают в стержне СВ:

Условие прочности имеет вид

где N – коэффициент запаса прочности. Для сталей n=1,52,5, примем n=2. Тогда допускаемые напряжения=845,7/2=422,85 МПа.

Условие прочности для заданной стержневой системы выполняется:

=164,9 МПа<=422,85 МПа.

Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00