Главная

Задача 1. Расчет статически неопределимых балок.

Для заданной статически неопределимой балки требуется:

1) раскрыть статическую неопределимость;

2) построить эпюру изгибающих моментов;

3) подобрать двутавровое сечение по условию прочности балки;

4) определить угол поворота сечения L и прогиб в сечении К.

Для всех вариантов принять: допускаемое напряжение [σ] = 160 МПа, модуль упругости E=2∙10⁵ МПа.

Числовые данные берутся из табл. 1, расчетные схемы – на рис. 1

Таблица 1

Номер строки	Схема по рис. 1	Нагрузка				Размер a, м
		q, кН/м	P, кН	P1, кН	m, кНм
01	1	5	10	10	4	1,0
02	2	4	8	5	6	1,5
03	3	8	6	8	4	1,0
04	4	10	8	12	2	0,8
05	5	12	5	7	5	1,2
06	6	6	7	10	7	1,0
07	7	5	10	6	3	1,2
08	8	10	11	9	4	0,8
09	9	8	8	7	5	0,6
10	10	7	5	10	6	1,0
	ж	з	а	б	в	г

1 схема 2 схема

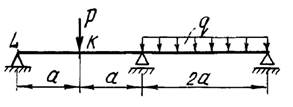
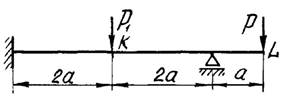
3 схема 4 схема

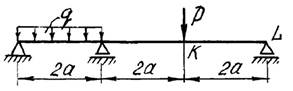
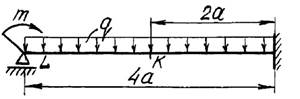
5 схема 6 схема

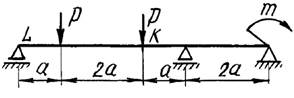
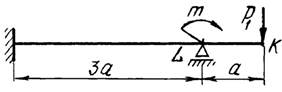
7 схема 8 схема

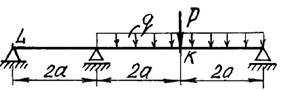
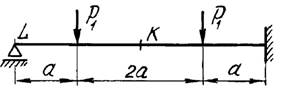
9 схема 10 схема

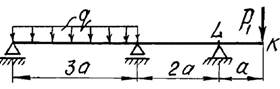
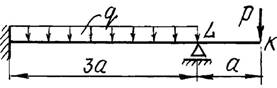
Рис. 1

Задача 2. Расчет статически неопределимых балок.

Исходные данные к задачам принимаются по табл. 2 и схемам на рис.2

1. Нарисуйте схему конструкции балки в масштабе. Отрицательные нагрузки направьте в сторону, противоположную показанной на рисунке. Покажите на рисунке размеры балки и величины нагрузок в численном виде.

2. Найдите степень статической неопределимости заданной системы.

3. Выберите основную систему, отбросив лишние связи, и приложите к основной системе лишние неизвестные (реакции в отброшенных связях).

4. Запишите условие совместности деформаций и раскройте его, определив деформации любым способом.

5. Из условия совместности деформаций найдите значение лишней неизвестной.

6. Постройте окончательные эпюры внутренних усилий.

7. Изобразите на рисунке изогнутую ось балки.

8. Выполните проверку, перемножив окончательную эпюру изгибающих моментов и эпюру моментов от единичной силы.

9*. Исследуйте, как изменится эпюра изгибающих моментов, если одну шарнирно подвижную опору сделать упругой (в виде пружины). Коэффициент жесткости пружины считайте заданной величиной.

Таблица 2

Номер строки	l2, м	q, кН/м	Схема по рис. 2	l1, м	l3, м	F, кН	M, кНм
01	2	10	1	1	1	20	0
02	3	20	2	4	1	0	40
03	4	30	3	2	1	-20	0
04	5	-30	4	2	3	0	-40
05	6	-20	5	1	4	30	0
06	5	-10	6	3	2	0	50
07	4	5	7	4	2	-30	0
08	3	-5	8	2	4	0	-50
09	2	15	9	3	3	40	0
10	5	-15	10	2	2	0	60
	в	г	а	б	в	г	а

1 схема 2 схема

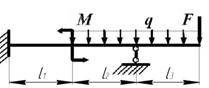
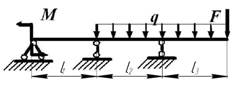
3 схема 4 схема

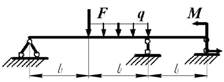
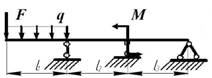
5 схема 6 схема

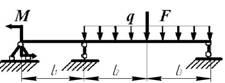
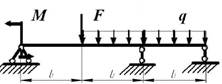
7 схема 8 схема

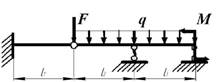
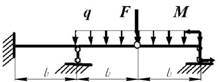
9 схема 10 схема

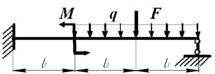
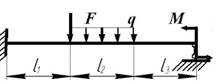
Рис. 2

Пример выполнения задач

Пример 1

Для статически неопределимой балки (рис.3, а) требуется:

1) раскрыть ее статическую неопределимость;

2) построить эпюру изгибающих моментов от действия внешних (пролетных) нагрузок;

3) подобрать двутавровое сечение балки из условия ее прочности;

4) определить угол поворота сечения L и прогиб балки в сечении К.

Дано: q = 6 кН/м; m = 4 кНм; а = 1,2 м; [s] = 160 МПа; E=2∙10⁵ Мпа.

Рис. 3. Статически неопределимая балка: а - заданная система; б - основная система;

в - эквивалентная система; г - грузовая эпюра M_p; д - единичная эпюра ; е - эпюра;

ж - окончательная эпюра M; з - эпюра от единичного момента ; и - эпюра от единичной силы

Решение.

1.Вычисляем степень статической неопределимости балки.

По условиям закрепления имеем четыре опорных реакции: две на опоре А и по одной на опорах В и С. Для плоской системы сил можно составить только три уравнения равновесия, поэтому степень статической неопределимости балки n = 4‑3 = 1, т.е. система один раз статически неопределима.

2.Выбираем основную систему.

Для этого разрезаем балку над средней опорой, тем самым, устраняя лишнюю связь, и вставляем над опорой промежуточный шарнир. «Лишней» неизвестной в этом случае будет изгибающий момент в опоре В, который обозначаем Х₁. На рис.3,б показана основная система. Загружая основную систему пролетными нагрузками и лишней неизвестной, получаем эквивалентную систему (рис.3,в). Достоинство принятой основной системы в том, что каждый пролет работает как самостоятельная балка и при построении эпюр может рассматриваться отдельно.

3. Строим в основной системе эпюру изгибающих моментов от заданной нагрузки M_p.

Рассмотрим участок АВ. Так как на этом участке нагрузок нет, для построения эпюры достаточно знать величины изгибающих моментов в сечениях А и В. На опоре А по условию М = m = 4 кНм; на опоре В изгибающий момент равен нулю (опорный момент Х₁ не учитываем), эпюра моментов ограничена прямой линией.

Рассмотрим участок ВС.

Вследствие симметрии пролетной нагрузки реакции опор будут одинаковыми:

Изгибающий момент в произвольном сечении x

и эпюра изгибающего момента ограничена квадратной параболой.

Строим эту параболу по трем лежащим на ней точкам:

x_B = 0, M_B= 0;

x = 1,2 м,

x_c = 2,4 м, M_c= 0.

Эпюра М_p показана на рис.3, г.

4. Строим эпюру от единичного момента .

В сечениях А и С изгибающие моменты равны нулю, а в сечении В изгибающий момент равен единице. Эпюра линейна, ее вид показан на рис.3, д.

5.Составляем каноническое уравнение метода сил

и вычисляем коэффициент δ₁₁ при неизвестном. Для этого эпюра умножается сама на себя. Чтобы упростить вычисления, разбиваем эпюру на два треугольника ADB и BDC и площадь каждого из них умножаем на ординату, расположенную в центре тяжести каждого из них (рис.3, д):

После подстановки числовых значений имеем

Для определения ∆_1р перемножаем эпюры М_P и (рис.3, г, д)

Площадь параболического сегмента вычисляется по формуле

где q - интенсивность распределенной нагрузки; l - длина участка балки под нагрузкой.

Вычисляем свободный член канонического уравнения ∆_1р:

Произведя соответствующие вычисления, получаем

Тогда каноническое уравнение принимает вид

откуда находим

Отрицательное значение X₁ говорит о том, что следует изменить направление момента X₁ на обратное.

6. Строим эпюру изгибающих моментов.

Считая момент X₁ внешней нагрузкой, можно определить опорные реакции, рассматривая каждый пролет балки отдельно, а затем построить эпюру моментов обычным способом, как это выполнялось для статически определимой балки. В данном случае удобнее воспользоваться уже построенными эпюрами.

Эквивалентная система находится под действием заданных пролетных нагрузок и вычисленного момента X₁. Следовательно, окончательная эпюра изгибающих моментов может быть представлена суммой двух эпюр

M=M_p + M_x1.

Первая эпюра уже построена (рис.3,г), а вторая получается умножением ординат эпюры (рис.31,д) на вычисленное значение X₁. Эпюра показана на рис.3,е. Геометрически складываем эпюры М_p и (рис.1,г,е), суммируя ординаты эпюр в характерных точках:

M_A=4+0= 4 кНм. M_E=4,32-1,47= 2,85 кНм.

M_B= 0-2,93= -2,93 кНм. M_C=0.

По найденным значениям М строим окончательно эпюру изгибающих моментов (рис.3, ж).

Для проверки правильности расчетов и построения эпюры изгибающих моментов можно использовать условие равенства нулю угла поворота смежных сечений балки над средней опорой (перемещение по направлению отброшенной связи). Этот угол вычисляется перемножением окончательной эпюры моментов (рис.3, ж) на эпюру (рис.3,д). При перемножении эпюру М удобно представить в виде трех треугольников, показанных пунктирными линиями на рис.3, ж, и параболического сегмента.

Угол поворота смежных сечений балки над средней опорой вычислим методом перемножения эпюр:

Площади эпюр и соответствующие ординаты под их центрами тяжести

определяются по соответствующим эпюрам (рис.3, ж) и (рис.3,д).

Итак,

Полученный результат свидетельствует о том, что эпюра изгибающих моментов построена правильно. Небольшая погрешность, не превышающая 5% , возникла в результате округлений.

7. Подбираем сечение балки по условию прочности.

При изгибе условие прочности имеет вид

По эпюре М (рис.3, ж) находим максимальный момент = 4 кНм, а по условию задачи [σ] = 160 МПа. Подставляя эти числа в последнюю формулу, получим величину требуемого момента сопротивления двутавра:

По таблицам сортамента прокатной стали подбираем номер двутавра и выписываем его геометрические характеристики: двутавр №10, W_x= 39,7 cм³, J_x = 198 см⁴.

(Момент сопротивления подобранного двутавра больше требуемого расчетного, но меньшего размера в таблице нет, поэтому принимаем двутавр №10).

8. Определяем перемещения.

Определяем угол поворота сечения L.

Для этого приложим в сечении L основной системы единичный момент и построим эпюру моментов (рис.3,з). Угол поворота сечения L вычисляем, перемножая эпюры М и (рис.3, ж,з):

Определяем прогиб в сечении К.

Приложим в сечении К основной системы единичную силу и построим от нее эпюру моментов (рис.3, и). Так как сила приложена в середине пролета AB, опорные реакции будут равны:

R_A = R_B = 0,5.

Определяем моменты в характерных точках участка АВ:

M_A = 0; М_K = 0,5∙1,8 = 0,9 м; M_B = 0.

Прогиб в сечении К вычисляется перемножением эпюр М и (рис.3,ж,и). Площадь при этом берем с эпюры М, а соответствующая ордината на эпюре равна величине средней линии трапеции, то есть алгебраической полусумме ее оснований:

Результат получен со знаком плюс, прогиб направлен в сторону приложенной единичной силы, то есть вниз.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00