Главная
Задача 1. Расчет статически определимых
консольных рам
Для рамы
(рис.1), соответствующей варианту
задания, с размерами
и нагрузкой, выбранными
по шифру из
табл.1, требуется:
1) определить опорные
реакции, используя уравнения
равновесия;
2) определить
участки, отличающиеся
характером нагружения
и отметить характерные точки приложения опорных реакций, сосредоточенных сил и
моментов, точки перегиба рамы, начало и конец
действия распределенной нагрузки;
3) на
каждом участке найти
значения изгибающего момента М, поперечной силы Q и продольной
силы N;
4) построить
эпюры М, Q и N;
5) выполнить
статическую проверку.
Таблица 1
|
Номер cтроки |
Схема по рис.1 |
F1, см2 |
а, м |
b, м |
М, кНм |
q, кН/м |
|
01 |
1 |
12 |
1 |
2 |
24 |
5 |
|
02 |
2 |
10 |
2 |
2 |
16 |
4 |
|
03 |
3 |
12 |
3 |
2 |
12 |
6 |
|
04 |
4 |
6 |
2 |
3 |
18 |
2 |
|
05 |
5 |
8 |
1 |
3 |
20 |
4 |
|
06 |
6 |
10 |
3 |
1 |
12 |
2 |
|
07 |
7 |
6 |
2 |
2 |
12 |
3 |
|
08 |
8 |
8 |
1 |
2 |
12 |
6 |
|
09 |
9 |
6 |
2 |
1 |
16 |
5 |
|
10 |
10 |
12 |
1 |
3 |
10 |
6 |
|
11 |
11 |
11 |
1 |
2 |
12 |
6 |
|
12 |
12 |
12 |
3 |
3 |
18 |
2 |
|
13 |
13 |
10 |
2 |
3 |
20 |
4 |
|
14 |
14 |
12 |
1 |
1 |
12 |
2 |
|
15 |
15 |
6 |
2 |
2 |
12 |
3 |
|
16 |
16 |
8 |
1 |
2 |
12 |
6 |
|
17 |
17 |
10 |
2 |
1 |
18 |
5 |
|
18 |
18 |
6 |
3 |
2 |
20 |
6 |
|
19 |
19 |
8 |
2 |
2 |
12 |
2 |
|
20 |
20 |
6 |
1 |
3 |
12 |
4 |
|
21 |
21 |
12 |
3 |
3 |
12 |
2 |
|
22 |
22 |
12 |
2 |
1 |
16 |
3 |
|
23 |
23 |
13 |
1 |
2 |
10 |
6 |
|
24 |
24 |
14 |
1 |
2 |
12 |
5 |
|
25 |
25 |
12 |
3 |
1 |
18 |
6 |
|
26 |
26 |
10 |
2 |
3 |
20 |
6 |
|
27 |
27 |
12 |
1 |
2 |
12 |
2 |
|
28 |
28 |
6 |
2 |
3 |
24 |
4 |
|
29 |
29 |
8 |
1 |
3 |
16 |
2 |
|
30 |
30 |
10 |
2 |
1 |
12 |
3 |
|
31 |
31 |
6 |
3 |
2 |
18 |
6 |
|
32 |
32 |
8 |
2 |
2 |
20 |
5 |
|
33 |
33 |
6 |
1 |
1 |
12 |
6 |
|
34 |
34 |
12 |
3 |
3 |
12 |
2 |
|
35 |
35 |
11 |
2 |
2 |
16 |
4 |
|
36 |
36 |
12 |
3 |
3 |
12 |
2 |
|
|
б |
б |
а |
г |
б |
а |
1 схема 2
схема
3 схема



4 схема 5 схема 6
схема



7 схема 8 схема 9
схема



10 схема 11 схема 12
схема



13 схема 14 схема 15 схема



16 схема 17 схема 18
схема



19 схема 20 схема 21 схема



22 схема 23 схема 24 схема



25 схема 26 схема 27 схема



28 схема 29 схема
30
схема



31 схема 32 схема 33 схема



34 схема 35 схема 36
схема



Рис.1
Задача 2. Расчет статически определимых
двухопорных рам
Для рамы
(рис.2), соответствующей варианту
задания, с размерами
и нагрузкой, выбранными по шифру
из табл.2, требуется:
1) определить опорные
реакции, используя уравнения
равновесия;
2) определить
участки, отличающиеся
характером нагружения и отметить
характерные точки приложения опорных реакций, сосредоточенных сил и моментов,
точки перегиба рамы, начало и конец
действия распределенной нагрузки;
3) на
каждом участке найти
значения изгибающего момента М, поперечной силы Q и продольной силы N;
4) построить
эпюры М, Q и N;
5) выполнить
статическую проверку.
Таблица 2
|
Номер cтроки |
Схема по рис.2 |
F1, см2 |
а, м |
b, м |
М, кНм |
q, кН/м |
|
01 |
1 |
12 |
1 |
2 |
24 |
5 |
|
02 |
2 |
10 |
2 |
2 |
16 |
4 |
|
03 |
3 |
12 |
3 |
2 |
12 |
6 |
|
04 |
4 |
6 |
2 |
3 |
18 |
2 |
|
05 |
5 |
8 |
1 |
3 |
20 |
4 |
|
06 |
6 |
10 |
3 |
1 |
12 |
2 |
|
07 |
7 |
6 |
2 |
2 |
12 |
3 |
|
08 |
8 |
8 |
1 |
2 |
12 |
6 |
|
09 |
9 |
6 |
2 |
1 |
16 |
5 |
|
10 |
10 |
12 |
1 |
3 |
10 |
6 |
|
11 |
11 |
11 |
1 |
2 |
12 |
6 |
|
12 |
12 |
12 |
3 |
3 |
18 |
2 |
|
13 |
13 |
10 |
2 |
3 |
20 |
4 |
|
14 |
14 |
12 |
1 |
1 |
12 |
2 |
|
15 |
15 |
6 |
2 |
2 |
12 |
3 |
|
16 |
16 |
8 |
1 |
2 |
12 |
6 |
|
17 |
17 |
10 |
2 |
1 |
18 |
5 |
|
18 |
18 |
6 |
3 |
2 |
20 |
6 |
|
19 |
19 |
8 |
2 |
2 |
12 |
2 |
|
20 |
20 |
6 |
1 |
3 |
12 |
4 |
|
21 |
21 |
12 |
3 |
3 |
12 |
2 |
|
22 |
22 |
12 |
2 |
1 |
16 |
3 |
|
23 |
23 |
13 |
1 |
2 |
10 |
6 |
|
24 |
24 |
14 |
1 |
2 |
12 |
5 |
|
25 |
25 |
12 |
3 |
1 |
18 |
6 |
|
26 |
26 |
10 |
2 |
3 |
20 |
6 |
|
27 |
27 |
12 |
1 |
2 |
12 |
2 |
|
28 |
28 |
6 |
2 |
3 |
24 |
4 |
|
29 |
29 |
8 |
1 |
3 |
16 |
2 |
|
30 |
30 |
10 |
2 |
1 |
12 |
3 |
|
31 |
31 |
6 |
3 |
2 |
18 |
6 |
|
32 |
32 |
8 |
2 |
2 |
20 |
5 |
|
33 |
33 |
6 |
1 |
1 |
12 |
6 |
|
34 |
34 |
12 |
3 |
3 |
12 |
2 |
|
35 |
35 |
11 |
2 |
2 |
16 |
4 |
|
36 |
36 |
12 |
3 |
3 |
12 |
2 |
|
|
г |
б |
в |
а |
б |
г |
1 схема 2 схема 3
схема



4 схема 5 схема 6
схема



7 схема 8 схема 9
схема



10 схема 11 схема 12
схема



13 схема 14 схема 15
схема



16 схема 17 схема 18 схема



19 схема 20 схема 21
схема



22 схема 23
схема
24 схема



25 схема 26 схема 27
схема



28 схема 29
схема
30 схема



31 схема 32 схема 33 схема



34 схема 35 схема 36 схема



Рис.2
Задача 3. Расчет статически
определимых шарнирно-опертых рам
Для рамы с
шарнирными опорами (рис.3),
соответствующей варианту задания,
с размерами и
нагрузкой, выбранными по шифру из табл.3, требуется построить эпюры внутренних силовых
факторов. Убедиться в равновесии узла А.
Таблица 3
|
Номер cтроки |
Схема по рис.3 |
F1/P |
F2/P |
l1/l |
l2/l |
l3/l |
|
01 |
I |
1,0 |
2,5 |
1,0 |
2,0 |
1,0 |
|
02 |
II |
2,0 |
3,0 |
1,0 |
1,0 |
1,0 |
|
03 |
III |
3,5 |
3,5 |
2,0 |
2,0 |
1,0 |
|
04 |
IV |
1,5 |
2,0 |
2,0 |
1,0 |
2,0 |
|
05 |
V |
2,0 |
2,5 |
1,0 |
1,0 |
2,0 |
|
06 |
VI |
3,5 |
1,0 |
2,0 |
1,0 |
2,0 |
|
07 |
VII |
2,5 |
1,7 |
1,0 |
2,0 |
1,0 |
|
08 |
VIII |
2,0 |
1,0 |
2,0 |
2,0 |
2,0 |
|
09 |
IX |
1,5 |
1,3 |
2,0 |
1,0 |
1,0 |
|
10 |
X |
1,0 |
1,4 |
1,0 |
1,0 |
2,0 |
|
11 |
I |
2,0 |
1,0 |
1,0 |
2,0 |
1,0 |
|
12 |
II |
1,0 |
2,0 |
1,0 |
1,0 |
1,0 |
|
13 |
III |
1,5 |
1,8 |
2,0 |
2,0 |
1,0 |
|
14 |
IV |
2,5 |
2,0 |
2,0 |
1,0 |
2,0 |
|
15 |
V |
3,0 |
2,0 |
1,0 |
1,0 |
2,0 |
|
16 |
VI |
3,5 |
1,0 |
2,0 |
1,0 |
2,0 |
|
17 |
VII |
2,0 |
1,1 |
1,0 |
2,0 |
1,0 |
|
18 |
VIII |
2,5 |
1,0 |
2,0 |
2,0 |
2,0 |
|
19 |
IX |
1,0 |
1,9 |
2,0 |
1,0 |
1,0 |
|
20 |
X |
1,7 |
1,5 |
1,0 |
1,0 |
2,0 |
|
21 |
I |
1,0 |
1,2 |
1,0 |
2,0 |
1,0 |
|
22 |
II |
1,3 |
2,5 |
1,0 |
1,0 |
1,0 |
|
23 |
III |
1,4 |
1,5 |
2,0 |
2,0 |
1,0 |
|
24 |
IV |
1,0 |
2,5 |
2,0 |
1,0 |
2,0 |
|
25 |
V |
2,0 |
3,0 |
1,0 |
1,0 |
2,0 |
|
26 |
VI |
1,8 |
3,5 |
2,0 |
1,0 |
2,0 |
|
27 |
VII |
2,0 |
2,0 |
1,0 |
2,0 |
1,0 |
|
28 |
VIII |
2,0 |
2,5 |
2,0 |
2,0 |
2,0 |
|
29 |
IX |
1,0 |
1,0 |
2,0 |
1,0 |
1,0 |
|
30 |
X |
1,1 |
1,7 |
1,0 |
1,0 |
2,0 |
|
31 |
I |
1,0 |
1,0 |
1,0 |
2,0 |
1,0 |
|
32 |
II |
1,9 |
1,3 |
1,0 |
1,0 |
1,0 |
|
33 |
III |
1,5 |
1,4 |
2,0 |
2,0 |
1,0 |
|
34 |
IV |
1,2 |
1,0 |
2,0 |
1,0 |
2,0 |
|
35 |
V |
2,5 |
2,0 |
1,0 |
1,0 |
2,0 |
|
36 |
VI |
1,5 |
1,8 |
2,0 |
1,0 |
2,0 |
|
|
в |
б |
в |
а |
б |
г |
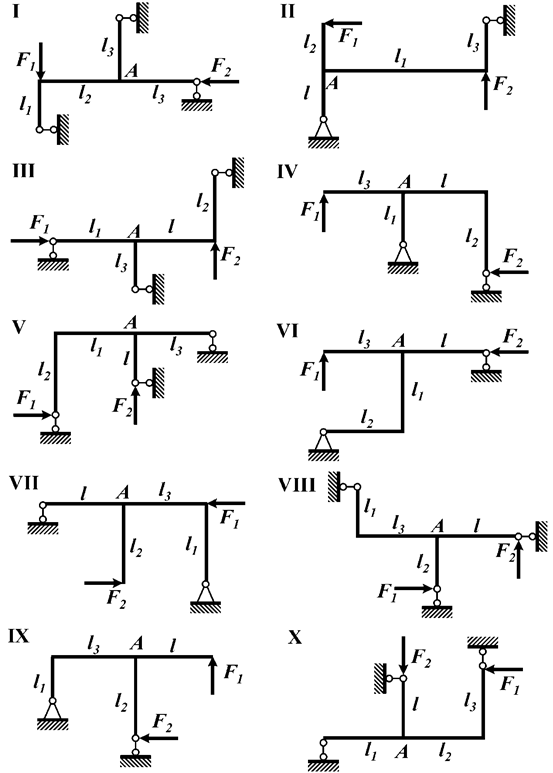
Рис.3
Задача 4. Расчет статически
определимых шарнирно-опертых рам
Для рамы с
шарнирными опорами (рис.4), нагруженной внешними сосредоточенными моментами M1 и М2, соответствующей варианту задания, с размерами
и нагрузкой, выбранными по шифру из табл.4, требуется построить эпюры
внутренних силовых факторов.
Таблица 3
|
Номер cтроки |
Схема по рис.4 |
M1/Pl |
M2/Pl |
l1/l |
l2/l |
l3/l |
|
01 |
I |
1 |
3 |
1,0 |
2,0 |
1,5 |
|
02 |
II |
2 |
1 |
1,0 |
3,0 |
2,0 |
|
03 |
III |
3 |
2 |
2,0 |
2,0 |
2,0 |
|
04 |
IV |
1 |
3 |
2,0 |
2,0 |
2,0 |
|
05 |
V |
2 |
1 |
1,0 |
2,0 |
1,5 |
|
06 |
VI |
3 |
1 |
2,0 |
1,5 |
2,0 |
|
07 |
VII |
1 |
2 |
1,0 |
3,0 |
1,5 |
|
08 |
VIII |
1 |
2 |
2,0 |
2,0 |
3,0 |
|
09 |
IX |
2 |
1 |
2,0 |
2,5 |
3,0 |
|
10 |
X |
2 |
2 |
1,0 |
3,0 |
2,0 |
|
11 |
I |
1 |
3 |
1,0 |
2,0 |
1,5 |
|
12 |
II |
2 |
1 |
1,0 |
3,0 |
2,0 |
|
13 |
III |
3 |
2 |
2,0 |
2,0 |
2,0 |
|
14 |
IV |
1 |
3 |
2,0 |
2,0 |
2,0 |
|
15 |
V |
2 |
1 |
1,0 |
2,0 |
1,5 |
|
16 |
VI |
3 |
1 |
2,0 |
1,5 |
2,0 |
|
17 |
VII |
1 |
2 |
1,0 |
3,0 |
1,5 |
|
18 |
VIII |
1 |
2 |
2,0 |
2,0 |
3,0 |
|
19 |
IX |
2 |
1 |
2,0 |
2,5 |
3,0 |
|
20 |
X |
2 |
2 |
1,0 |
3,0 |
2,0 |
|
21 |
I |
1 |
3 |
1,0 |
2,0 |
1,5 |
|
22 |
II |
2 |
1 |
1,0 |
3,0 |
2,0 |
|
23 |
III |
3 |
2 |
2,0 |
2,0 |
2,0 |
|
24 |
IV |
1 |
3 |
2,0 |
2,0 |
2,0 |
|
25 |
V |
2 |
1 |
1,0 |
2,0 |
1,5 |
|
26 |
VI |
3 |
1 |
2,0 |
1,5 |
2,0 |
|
27 |
VII |
1 |
2 |
1,0 |
3,0 |
1,5 |
|
28 |
VIII |
1 |
2 |
2,0 |
2,0 |
3,0 |
|
29 |
IX |
2 |
1 |
2,0 |
2,5 |
3,0 |
|
30 |
X |
2 |
2 |
1,0 |
3,0 |
2,0 |
|
31 |
I |
1 |
3 |
1,0 |
2,0 |
1,5 |
|
32 |
II |
2 |
1 |
1,0 |
3,0 |
2,0 |
|
33 |
III |
3 |
2 |
2,0 |
2,0 |
2,0 |
|
34 |
IV |
1 |
3 |
2,0 |
2,0 |
2,0 |
|
35 |
V |
2 |
1 |
1,0 |
2,0 |
1,5 |
|
36 |
VI |
3 |
1 |
2,0 |
1,5 |
2,0 |
|
|
а |
в |
г |
а |
б |
г |
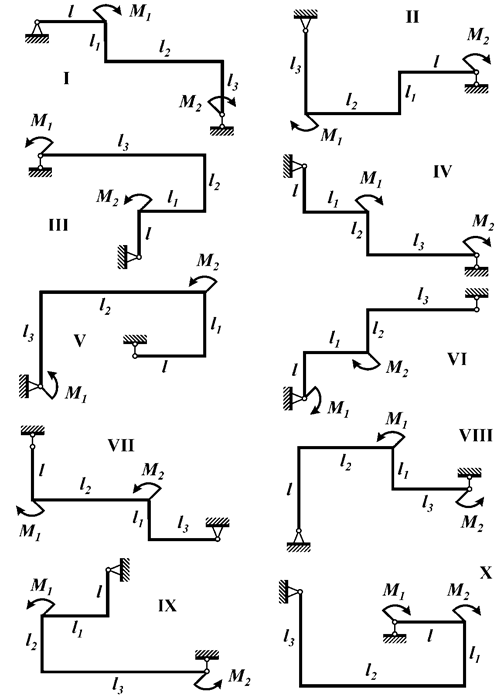
Рис.4
Задача 5. Расчет статически
определимых консольных рам
Для плоской
консольной рамы (рис.5),
соответствующей варианту задания,
с размерами и
нагрузкой, выбранными по шифру из табл.5, требуется построить эпюры внутренних силовых
факторов. Убедиться в равновесии узла А.
Таблица 5
|
Номер cтроки |
Схема по рис.5 |
F1/P |
F2/P |
F3/P |
l1/l |
l2/l |
l3/l |
|
01 |
I |
1,0 |
2,5 |
1,0 |
1,0 |
3,0 |
1,0 |
|
02 |
II |
2,0 |
3,0 |
2,0 |
1,5 |
1,5 |
2,5 |
|
03 |
III |
3,5 |
3,5 |
1,0 |
1,0 |
2,5 |
1,0 |
|
04 |
IV |
1,5 |
2,0 |
1,5 |
1,5 |
1,0 |
3,0 |
|
05 |
V |
2,0 |
2,5 |
2,5 |
3,0 |
2,0 |
2,0 |
|
06 |
VI |
3,5 |
1,0 |
3,0 |
2,5 |
1,5 |
2,5 |
|
07 |
VII |
2,5 |
1,7 |
3,5 |
2,0 |
3,0 |
1,5 |
|
08 |
VIII |
2,0 |
1,0 |
2,0 |
2,5 |
2,0 |
2,0 |
|
09 |
IX |
1,5 |
1,3 |
2,5 |
3,0 |
1,0 |
3,0 |
|
10 |
X |
1,0 |
1,4 |
1,0 |
2,0 |
2,5 |
1,5 |
|
11 |
I |
2,0 |
1,0 |
1,7 |
1,0 |
3,0 |
1,0 |
|
12 |
II |
1,0 |
2,0 |
1,0 |
1,5 |
1,5 |
2,5 |
|
13 |
III |
1,5 |
1,8 |
1,3 |
1,0 |
2,5 |
1,0 |
|
14 |
IV |
2,5 |
2,0 |
1,4 |
1,5 |
1,0 |
3,0 |
|
15 |
V |
3,0 |
2,0 |
1,0 |
3,0 |
2,0 |
2,0 |
|
16 |
VI |
3,5 |
1,0 |
2,0 |
2,5 |
1,5 |
2,5 |
|
17 |
VII |
2,0 |
1,1 |
1,8 |
2,0 |
3,0 |
1,5 |
|
18 |
VIII |
2,5 |
1,0 |
2,0 |
2,5 |
2,0 |
2,0 |
|
19 |
IX |
1,0 |
1,9 |
2,0 |
3,0 |
1,0 |
3,0 |
|
20 |
X |
1,7 |
1,5 |
1,0 |
2,0 |
2,5 |
1,5 |
|
21 |
I |
1,0 |
1,2 |
1,1 |
1,0 |
3,0 |
1,0 |
|
22 |
II |
1,3 |
2,5 |
1,0 |
1,5 |
1,5 |
2,5 |
|
23 |
III |
1,4 |
1,5 |
1,9 |
1,0 |
2,5 |
1,0 |
|
24 |
IV |
1,0 |
2,5 |
1,5 |
1,5 |
1,0 |
3,0 |
|
25 |
V |
2,0 |
3,0 |
1,2 |
3,0 |
2,0 |
2,0 |
|
26 |
VI |
1,8 |
3,5 |
2,5 |
2,5 |
1,5 |
2,5 |
|
27 |
VII |
2,0 |
2,0 |
1,5 |
2,0 |
3,0 |
1,5 |
|
28 |
VIII |
2,0 |
2,5 |
1,0 |
2,5 |
2,0 |
2,0 |
|
29 |
IX |
1,0 |
1,0 |
2,0 |
3,0 |
1,0 |
3,0 |
|
30 |
X |
1,1 |
1,7 |
1,0 |
2,0 |
2,5 |
1,5 |
|
31 |
I |
1,0 |
1,0 |
1,5 |
1,0 |
3,0 |
1,0 |
|
32 |
II |
1,9 |
1,3 |
2,5 |
1,5 |
1,5 |
2,5 |
|
33 |
III |
1,5 |
1,4 |
3,0 |
1,0 |
2,5 |
1,0 |
|
34 |
IV |
1,2 |
1,0 |
3,5 |
1,5 |
1,0 |
3,0 |
|
35 |
V |
2,5 |
2,0 |
2,0 |
3,0 |
2,0 |
2,0 |
|
36 |
VI |
1,5 |
1,8 |
2,5 |
2,5 |
1,5 |
2,5 |
|
|
в |
б |
г |
в |
а |
б |
г |
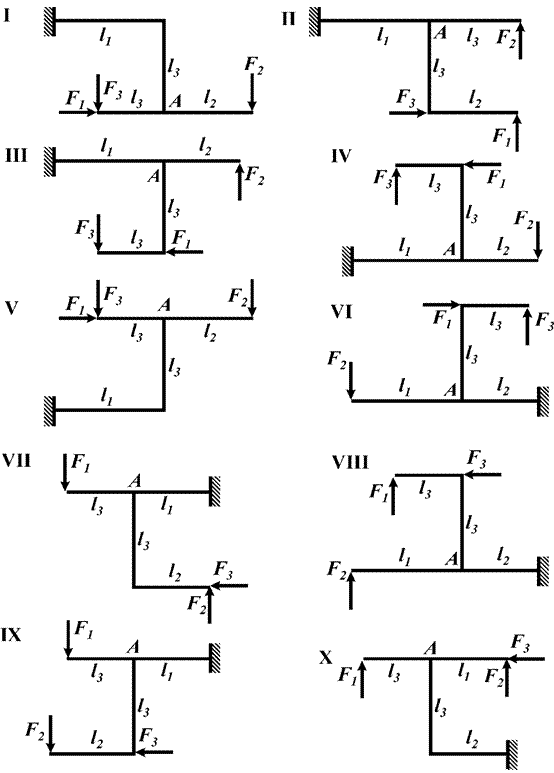
Рис.5
Задача 6. Расчет статически
определимых консольных рам
Для плоской
консольной рамы (рис.6),
соответствующей варианту задания,
с размерами и
нагрузкой, выбранными по шифру из табл.6, требуется построить эпюры внутренних силовых
факторов. Убедиться в равновесии узла А.
Таблица 6
|
Номер cтроки |
Схема по рис.6 |
M/ql2 |
F/ql |
q1/q |
l1/l |
l2/l |
l3/l |
|
01 |
I |
1,0 |
–3,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
02 |
II |
2,0 |
1,0 |
2,0 |
2,0 |
1,0 |
3,0 |
|
03 |
III |
3,0 |
2,0 |
3,0 |
1,0 |
2,0 |
4,0 |
|
04 |
IV |
–1,0 |
3,0 |
2,0 |
1,5 |
1,5 |
3,0 |
|
05 |
V |
–2,0 |
2,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
06 |
VI |
–3,0 |
1,0 |
–1,0 |
2,0 |
1,0 |
3,0 |
|
07 |
VII |
1,5 |
–1,0 |
–2,0 |
1,5 |
2,0 |
1,0 |
|
08 |
VIII |
–0,5 |
–2,0 |
–3,0 |
1,5 |
1,0 |
3,0 |
|
09 |
IX |
–1,5 |
–3,0 |
–2,0 |
1,0 |
2,0 |
2,0 |
|
10 |
X |
1,5 |
–2,0 |
–1,0 |
2,0 |
1,5 |
3,0 |
|
11 |
I |
1,0 |
–3,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
12 |
II |
2,0 |
1,0 |
2,0 |
2,0 |
1,0 |
3,0 |
|
13 |
III |
3,0 |
2,0 |
3,0 |
1,0 |
2,0 |
4,0 |
|
14 |
IV |
–1,0 |
3,0 |
2,0 |
1,5 |
1,5 |
3,0 |
|
15 |
V |
–2,0 |
2,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
16 |
VI |
–3,0 |
1,0 |
–1,0 |
2,0 |
1,0 |
3,0 |
|
17 |
VII |
1,5 |
–1,0 |
–2,0 |
1,5 |
2,0 |
1,0 |
|
18 |
VIII |
–0,5 |
–2,0 |
–3,0 |
1,5 |
1,0 |
3,0 |
|
19 |
IX |
–1,5 |
–3,0 |
–2,0 |
1,0 |
2,0 |
2,0 |
|
20 |
X |
1,5 |
–2,0 |
–1,0 |
2,0 |
1,5 |
3,0 |
|
21 |
I |
1,0 |
–3,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
22 |
II |
2,0 |
1,0 |
2,0 |
2,0 |
1,0 |
3,0 |
|
23 |
III |
3,0 |
2,0 |
3,0 |
1,0 |
2,0 |
4,0 |
|
24 |
IV |
–1,0 |
3,0 |
2,0 |
1,5 |
1,5 |
3,0 |
|
25 |
V |
–2,0 |
2,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
26 |
VI |
–3,0 |
1,0 |
–1,0 |
2,0 |
1,0 |
3,0 |
|
27 |
VII |
1,5 |
–1,0 |
–2,0 |
1,5 |
2,0 |
1,0 |
|
28 |
VIII |
–0,5 |
–2,0 |
–3,0 |
1,5 |
1,0 |
3,0 |
|
29 |
IX |
–1,5 |
–3,0 |
–2,0 |
1,0 |
2,0 |
2,0 |
|
30 |
X |
1,5 |
–2,0 |
–1,0 |
2,0 |
1,5 |
3,0 |
|
31 |
I |
1,0 |
–3,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
32 |
II |
2,0 |
1,0 |
2,0 |
2,0 |
1,0 |
3,0 |
|
33 |
III |
3,0 |
2,0 |
3,0 |
1,0 |
2,0 |
4,0 |
|
34 |
IV |
–1,0 |
3,0 |
2,0 |
1,5 |
1,5 |
3,0 |
|
35 |
V |
–2,0 |
2,0 |
1,0 |
1,0 |
1,5 |
2,0 |
|
36 |
VI |
–3,0 |
1,0 |
–1,0 |
2,0 |
1,0 |
3,0 |
|
|
а |
г |
б |
в |
а |
б |
г |
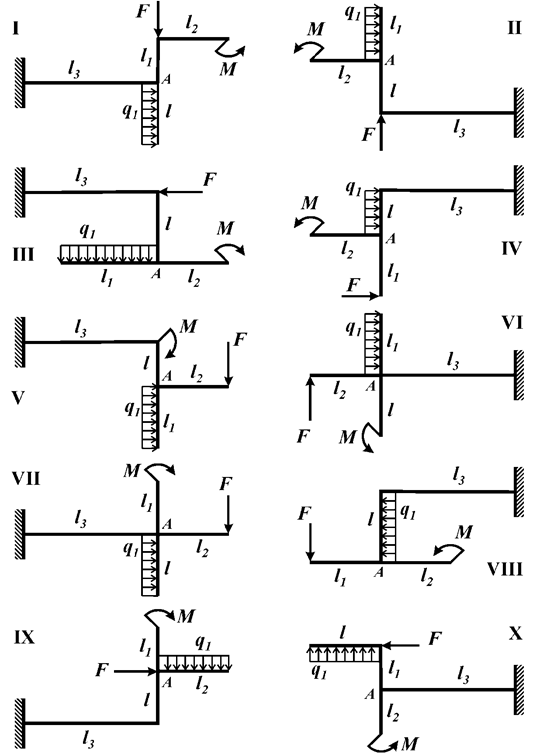
Рис.6
Задача 7. Расчет статически
определимых шарнирно-опертых рам
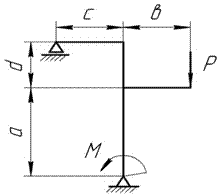
Для плоской
шарнирно-опертой рамы (рис.7),
соответствующей варианту задания,
с размерами и
нагрузкой, выбранными по шифру из табл.7, требуется построить эпюры
внутренних силовых факторов.
Таблица 7
|
Номер cтроки |
Схема по рис.7 |
a, м |
b, м |
c, м |
d, м |
P, кН |
M, кНм |
|
01 |
1 |
1 |
2 |
2 |
1 |
6 |
24 |
|
02 |
2 |
2,5 |
2 |
1 |
3,5 |
1 |
16 |
|
03 |
3 |
3 |
2 |
3 |
2 |
2 |
12 |
|
04 |
4 |
2 |
3 |
2 |
1 |
4 |
18 |
|
05 |
5 |
1 |
3 |
3 |
2 |
4 |
20 |
|
06 |
6 |
3 |
1 |
3 |
1 |
6 |
12 |
|
07 |
7 |
2 |
2 |
1 |
2 |
6 |
12 |
|
08 |
8 |
1 |
2 |
2 |
3 |
4 |
12 |
|
09 |
9 |
2 |
1 |
2 |
2 |
2 |
16 |
|
10 |
10 |
1,7 |
3 |
1 |
1 |
4 |
10 |
|
11 |
11 |
1,3 |
2 |
2 |
3 |
6 |
12 |
|
12 |
12 |
3 |
3 |
2 |
2 |
1 |
18 |
|
13 |
13 |
2 |
3 |
1 |
1,5 |
2 |
20 |
|
14 |
14 |
1,1 |
1 |
3 |
1,2 |
4 |
12 |
|
15 |
15 |
2,1 |
2,5 |
2,5 |
3 |
4 |
12 |
|
16 |
16 |
1 |
2,3 |
3 |
2 |
6 |
12 |
|
17 |
17 |
2 |
1 |
3 |
1 |
6 |
18 |
|
18 |
18 |
3 |
2 |
1,6 |
2 |
4 |
20 |
|
19 |
19 |
2 |
2 |
2 |
1,9 |
2 |
12 |
|
20 |
20 |
1,5 |
3 |
2 |
3 |
4 |
12 |
|
21 |
21 |
3 |
3,4 |
1 |
2 |
6 |
12 |
|
22 |
22 |
2 |
1 |
2 |
1 |
1 |
16 |
|
23 |
23 |
1 |
2 |
2 |
2 |
2 |
10 |
|
24 |
24 |
1 |
2 |
1 |
1,5 |
4 |
12 |
|
25 |
1 |
3 |
1 |
3 |
2 |
4 |
18 |
|
26 |
2 |
2 |
3 |
2 |
3 |
6 |
20 |
|
27 |
3 |
1,9 |
2 |
3 |
2 |
6 |
12 |
|
28 |
4 |
2 |
3 |
3 |
1 |
4 |
24 |
|
29 |
5 |
1 |
3 |
1,5 |
3,2 |
2 |
16 |
|
30 |
6 |
2 |
1,1 |
2 |
2 |
4 |
12 |
|
31 |
7 |
3 |
2 |
2 |
1 |
6 |
18 |
|
32 |
8 |
2 |
2 |
1 |
1,5 |
1 |
20 |
|
33 |
9 |
1,3 |
1 |
2,3 |
3 |
2 |
12 |
|
34 |
10 |
3 |
3 |
2 |
2 |
4 |
12 |
|
35 |
11 |
2 |
2 |
1 |
1 |
4 |
16 |
|
36 |
12 |
3 |
3,1 |
3 |
2 |
6 |
12 |
|
|
а |
г |
б |
в |
а |
б |
г |
1 схема 2 схема 3
схема


4 схема 5 схема
6 схема



7 схема 8 схема
9 схема



10 схема 11 схема 12 схема



13 схема 14 схема
15 схема



16 схема
17 схема 18
схема



19 схема 20 схема 21
схема



22 схема 23 схема 24
схема



Рис.7
Задача 8. Расчет статически
определимых консольных и двухопорных рам
Для
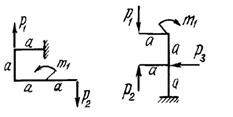
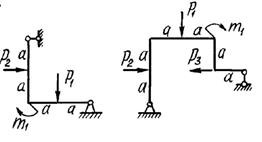
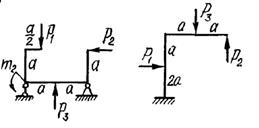
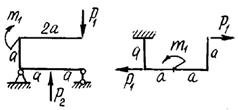
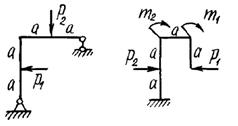
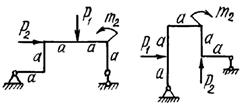
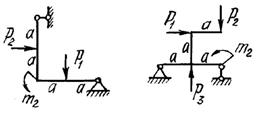
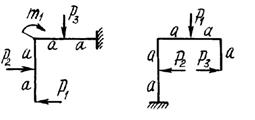
двух заданных плоских рам построить эпюры изгибающих моментов.
Схемы
рам и числовые данные для решения задачи выбираются из табл. 8 и на рис.8.
Таблица 8
|
Номер строки |
Схема по рис.8 |
Сила, кН |
Момент, кНм |
Размер а, м |
|||
|
P1 |
P2 |
P3 |
M1 |
M2 |
|||
|
01 |
1 |
10 |
12 |
6 |
4 |
6 |
2 |
|
02 |
2 |
8 |
4 |
1 |
5 |
5 |
1 |
|
03 |
3 |
2 |
4 |
2 |
6 |
4 |
2 |
|
04 |
4 |
10 |
6 |
4 |
2 |
8 |
2 |
|
05 |
5 |
6 |
4 |
4 |
4 |
6 |
2 |
|
06 |
6 |
8 |
6 |
6 |
6 |
4 |
1 |
|
07 |
7 |
2 |
2 |
6 |
5 |
2 |
2 |
|
08 |
8 |
2 |
5 |
4 |
2 |
8 |
2 |
|
09 |
9 |
5 |
10 |
2 |
4 |
4 |
2 |
|
10 |
10 |
2 |
4 |
4 |
5 |
4 |
1 |
|
|
з |
ж |
а |
б |
в |
г |
д |
1 схема
2 схема
3
схема 4
схема
5
схема 6
схема
7
схема 8
схема
9 схема
10 схема
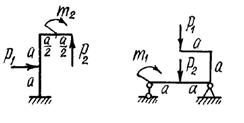
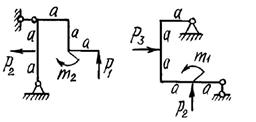
Рис. 8
Задача 9. Расчет статически
определимых плоских замкнутых рам
Из условия равновесия плоской замкнутой рамы (рис.9),
с размерами и нагрузкой, выбранными по шифру из табл.9, требуется:
1) определить величину внешнего сосредоточенного
момента М.
2) построить эпюры внутренних силовых факторов.
Таблица 9
|
Номер cтроки |
Схема по рис.9 |
l1/l |
l2/l |
l3/l |
|
01 |
I |
1 |
2/3 |
1/3 |
|
02 |
II |
2 |
1/3 |
1/2 |
|
03 |
III |
1 |
1/2 |
2/3 |
|
04 |
IV |
2 |
1/4 |
1/2 |
|
05 |
V |
1 |
3/4 |
1/3 |
|
06 |
VI |
2 |
2/3 |
1/2 |
|
07 |
VII |
1 |
1/3 |
2/3 |
|
08 |
VIII |
2 |
1/2 |
1/3 |
|
09 |
I |
1 |
1/4 |
1/2 |
|
10 |
II |
2 |
3/4 |
2/3 |
|
11 |
III |
1 |
2/3 |
1/3 |
|
12 |
IV |
2 |
1/3 |
1/2 |
|
13 |
V |
1 |
1/2 |
2/3 |
|
14 |
VI |
2 |
1/4 |
1/2 |
|
15 |
VII |
1 |
3/4 |
1/3 |
|
16 |
VIII |
2 |
2/3 |
1/2 |
|
17 |
I |
1 |
1/3 |
2/3 |
|
18 |
II |
2 |
1/2 |
1/3 |
|
19 |
III |
1 |
1/4 |
1/2 |
|
20 |
IV |
2 |
3/4 |
2/3 |
|
21 |
V |
1 |
2/3 |
1/3 |
|
22 |
VI |
2 |
1/3 |
1/2 |
|
23 |
VII |
1 |
1/2 |
2/3 |
|
24 |
VIII |
2 |
1/4 |
1/2 |
|
25 |
I |
1 |
3/4 |
1/3 |
|
26 |
II |
2 |
2/3 |
1/2 |
|
27 |
III |
1 |
1/3 |
2/3 |
|
28 |
IV |
2 |
1/2 |
1/3 |
|
29 |
V |
1 |
1/4 |
1/2 |
|
30 |
VI |
2 |
3/4 |
2/3 |
|
31 |
VII |
1 |
2/3 |
1/3 |
|
32 |
VIII |
2 |
1/3 |
1/2 |
|
33 |
I |
1 |
1/2 |
2/3 |
|
34 |
II |
2 |
1/4 |
1/2 |
|
35 |
III |
1 |
3/4 |
1/3 |
|
36 |
IV |
2 |
2/3 |
1/2 |
|
|
в |
а |
б |
г |
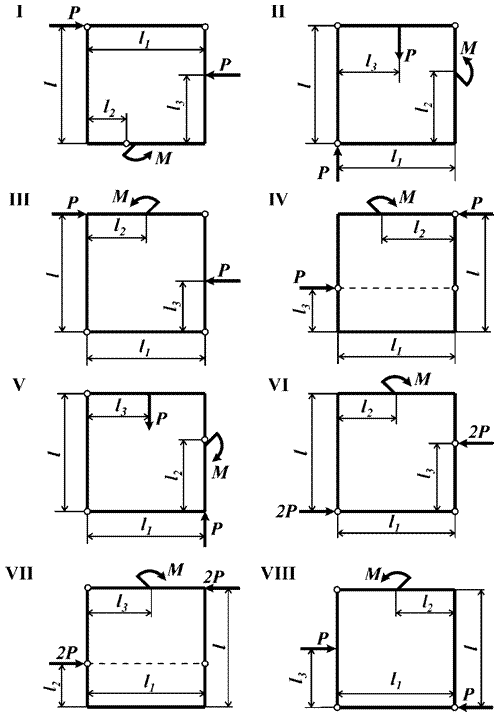
Рис.9
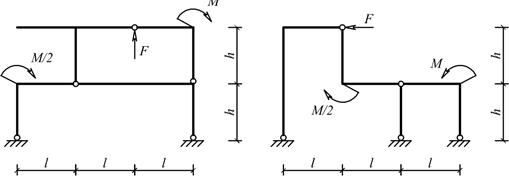
Задача 10. Расчет статически
определимых плоских составных рам
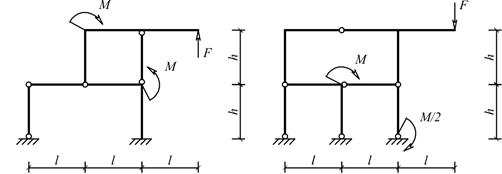
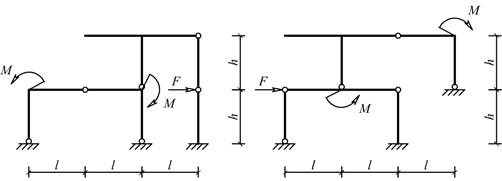
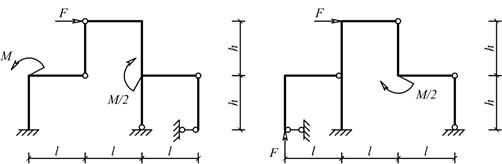
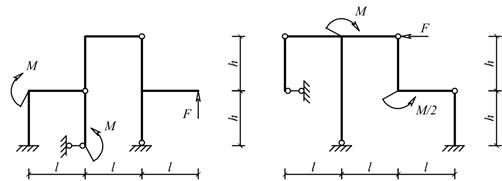
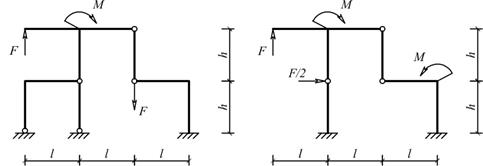
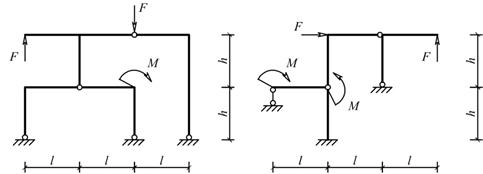
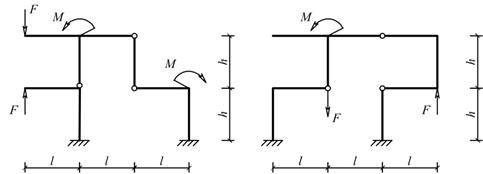
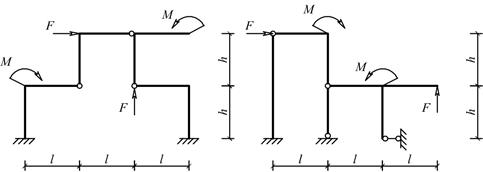
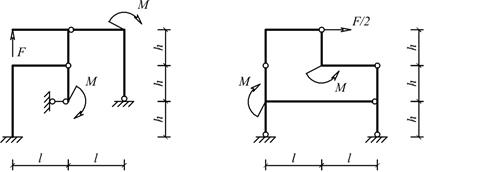
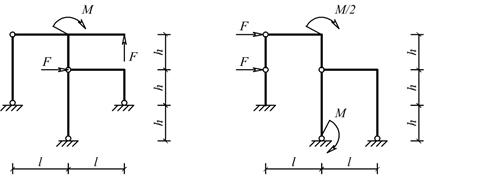
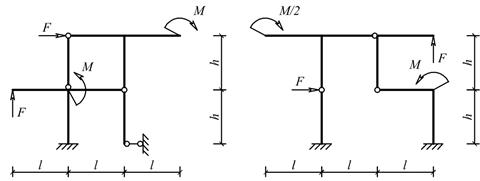
Для одной из рам, изображенных на рис. 10, требуется:
1) выполнить
кинематический анализ;
2) определить реакции
в связях, включая силы взаимодействия в шарнирах;
3) построить
эпюры внутренних силовых факторов.
Исходные данные для расчета принять из табл.10.
Таблица 10
|
Номер строки |
Схемы балок по рис. 10 |
h, м |
l, м |
M, кНм |
F, кН |
|
01 |
1 |
3 |
2 |
6 |
4 |
|
02 |
2 |
4 |
3 |
5 |
5 |
|
03 |
3 |
2 |
4 |
4 |
3 |
|
04 |
4 |
4 |
2 |
6 |
6 |
|
05 |
5 |
3 |
2 |
8 |
7 |
|
06 |
6 |
2 |
4 |
10 |
2 |
|
07 |
7 |
3 |
3 |
7 |
8 |
|
08 |
8 |
2 |
5 |
10 |
3 |
|
09 |
9 |
5 |
1 |
9 |
4 |
|
10 |
10 |
4 |
2 |
8 |
7 |
|
11 |
11 |
1 |
4 |
7 |
8 |
|
12 |
12 |
3 |
3 |
6 |
3 |
|
13 |
13 |
5 |
2 |
5 |
6 |
|
14 |
14 |
2 |
5 |
2 |
5 |
|
15 |
15 |
4 |
3 |
5 |
2 |
|
16 |
16 |
1 |
4 |
6 |
8 |
|
17 |
17 |
3 |
3 |
7 |
5 |
|
18 |
18 |
5 |
1 |
8 |
3 |
|
19 |
19 |
1 |
2 |
9 |
4 |
|
20 |
20 |
2 |
5 |
10 |
8 |
|
21 |
21 |
4 |
3 |
4 |
9 |
|
22 |
22 |
3 |
2 |
5 |
2 |
|
23 |
23 |
2 |
4 |
8 |
3 |
|
24 |
24 |
1 |
2 |
7 |
5 |
|
25 |
25 |
5 |
1 |
6 |
7 |
|
26 |
26 |
2 |
5 |
4 |
6 |
|
27 |
1 |
5 |
2 |
5 |
6 |
|
28 |
2 |
2 |
5 |
2 |
5 |
|
29 |
3 |
4 |
3 |
5 |
2 |
|
30 |
4 |
1 |
4 |
6 |
8 |
|
31 |
5 |
3 |
3 |
7 |
5 |
|
32 |
6 |
5 |
1 |
8 |
3 |
|
33 |
7 |
1 |
2 |
9 |
4 |
|
34 |
8 |
2 |
5 |
10 |
8 |
|
35 |
9 |
4 |
3 |
4 |
9 |
|
36 |
10 |
3 |
3 |
9 |
8 |
|
|
г |
в |
б |
а |
в |
1 схема
2
схема
3 схема
4
схема
5 схема
6
схема
7 схема
8
схема
9 схема
10
схема
11 схема
12
схема
13 схема
14
схема
15 схема
16
схема
17 схема
18
схема
19 схема
20
схема
21 схема
22
схема
23 схема
24
схема
25 схема
26
схема
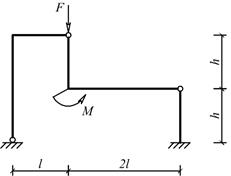
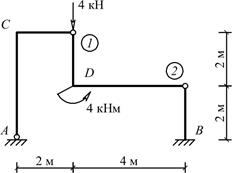
Рис.10
Примеры выполнения
задач
Пример 1
Для заданной рамы (рис.11,a) построить эпюру изгибающих моментов при следующих
исходных данных: P1=2P, P2=P, M2=Pa.
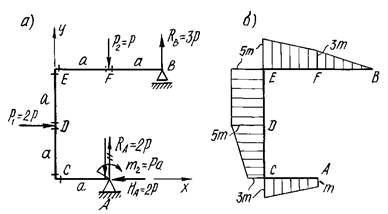
Рис. 11.
Расчетная схема рамы и эпюра изгибающих моментов
Решение.
Определяем
опорные реакции рамы. На расчетной схеме (рис.11, a) показываем векторы
опорных реакций RA и HA шарнирно-неподвижной опоры и
вектор RB на шарнирно-подвижной опоре B. Величины реакций
определяются из уравнений равновесия рамы:
ΣX= 0; P1 - HA= 0; HA=P1= 2P;
ΣmB=0;
-RA∙a
- m2 - HA∙2a+P1∙a+P2∙a= 0;
-RA∙a - Pa - 2P∙2a + 2P∙a + Pa=0; RA= -2P;
ΣmA=
0; RB∙a
- P1∙a - P1∙a - m2= 0;
RB∙a - 2P∙a - P∙a
= 0; RB=3P.
Реакция RА
отрицательна, а это значит, что ее направление было выбрано неправильно и его
надо изменить на противоположное. В дальнейших
расчетах знак минус не учитывается.
Для
проверки правильности вычисления опорных реакций подсчитывается сумма проекций
сил, приложенных к раме, на вертикальную ось Y:
ΣY = -RA -
P2 + RB = -2P - P + 3P = 0.
Равенство этой суммы нулю говорит о том, что реакции определены правильно.
Разбиваем раму на участки, границы которых на рис.11,а обозначены латинскими буквами. В
граничных сечениях каждого участка находим величины изгибающих моментов и
откладываем полученные значения со стороны сжатого волокна (для удобства
построений введем обозначение m=Pa).
С целью вычисления изгибающего момента рассекаем мысленно раму в
исследуемом сечении на две части и отбрасываем одну из них, а затем
подсчитываем алгебраическую сумму моментов всех сил, приложенных к оставшейся
части, относительно рассматриваемого сечения. Эта сумма равна величине
изгибающего момента в данном сечении рамы.
Рассмотрим последовательно стержни рамы, начиная со стержня AC, который имеет лишь один участок.
Мысленно рассекая стержень в начале участка (левее точки A) и отбрасывая левую часть рамы, вычисляем изгибающий момент в
начале участка:
MA=m2=Pa, (сжатые
волокна при этом будут находиться снизу).
В конце участка (точка C)
величина изгибающего момента равна алгебраической сумме моментов от действия
пары сил m2 и реакции RA.
Пара сил изгибает стержень AC таким
образом, что его сжатые волокна располагаются
снизу. Будем считать условно изгибающий момент в сечении С, возникающий от
действия пары сил, положительным. Тогда
изгибающий момент в том же сечении от действия реакции RA следует считать положительным, так как эта сила так же, как и пара сил m2, вызывает сжатие нижних волокон стержня.
Изгибающий момент в сечении С
MC =
m2 + RA∙a=P∙a + 2P∙a = 3Pa.
Положительное значение изгибающего момента означает, что сжатые волокна
стержня в сечении С
по-прежнему остаются снизу.
Откладывая в масштабе полученные значения изгибающих моментов перпендикулярно
оси стержня AC вниз (со стороны
сжатых волокон), строим на этом участке эпюру M, которая будет ограничена прямой линией, так как к раме не приложены
распределенные нагрузки.
Переходим к следующему стержню - CE,
который разбиваем на два участка - CD и DE.
Участок CD. Изгибающий
момент в сечении C, которое
принадлежит одновременно стержням AC и CE известен: MC =3Pa.
Сжатые волокна стержня CE в сечении C находится слева от его оси, следовательно, момент MC
= 3Pa надо отложить влево. Изгибающий момент в сечении D
MD=m2 + RA∙a + HA∙a=P∙a + 2P∙a + 2P∙a= 5Pa.
Положительное значение изгибающего момента MD означает,
что сжатые волокна стержня, как и в сечении C, расположены слева.
Участок DE. Изгибающий момент в сечении D, которое принадлежит теперь рассматриваемому участку DE, MD = 5Pa. Находим
изгибающий момент в сечении E:
ME =
m2 + RA∙a + HA∙2a - P1∙a=P∙a + 2P∙a + 2P∙2a - 2P∙a = 5P∙a.
Перед моментом от силы P1
поставлен знак минус, так как сила P1
сжимает волокна, располагающиеся справа
от оси стержня. Положительное значение
момента ME
= 5Pa означает,
что сжатые волокна в сечении располагается слева.
Откладывая ординаты эпюры перпендикулярно оси стержня, как это делалось
ранее, строим эпюру на участке DE.
Построение эпюры изгибающих моментов для стержня BE удобно производить, перемещаясь от сечения B справа налево.
Стержень BE. Разбиваем его на два участка: BF и FE. Изгибающий
момент в сечении B равен нулю. В
сечении F участка BF стержня
изгибающий момент равен моменту от действия силы RB
= 3P, его величина
MF =
RB∙a = 3P∙a (сжатые
волокна находится сверху).
Участок FE. Изгибающий момент в сечении
F, принадлежащем этому участку,
известен: M=3Pa. В конце
участка (сечение E) изгибающий
момент:
ME =
RB∙2a - P2∙a = 3P∙2a - P∙a = 5P∙a.
Первое слагаемое, представляющее момент от действия силы RB, вызывающей сжатие верхних волокон стержня, принято положительным. Перед вторым
слагаемым поставлен знак минус, так как сжатые волокна от действия силы P2
расположены снизу.
Положительное значение изгибающего момента в сечении E означает, что сжатые
волокна стержня в этом сечении находятся сверху от его оси. Вычисленные ординаты откладываются на эпюре
вверх от оси стержня - со стороны сжатых волокон (рис.11, б).
Следует обратить внимание на то, что при переходе через узел изгибающий
момент по модулю не изменяется и эпюра располагается по одну сторону от контура
рамы (внутри или снаружи). Это условие соблюдается, если в узле рамы не
приложен сосредоточенный момент (пара сил).
Пример 2
Требуется построить эпюру изгибающих моментов для рамы, показанной на
рис.12, a.
Исходные
данные для расчета: P1 = 2P;
P2 = 3P; m1 =
2Pa.
Решение.
Для рамы, жестко защемленной одним концом, построение эпюры изгибающих
моментов рекомендуется начинать с незакрепленного сечения (сечение A на рис.12, а), не определяя опорных реакций.
Стержень AB (рис.12,а) имеет один участок, в начале и конце
которого вычисляются изгибающие моменты:
ΣMA = 0, MB = P1∙a = 2P∙a .
Откладываем найденные значения слева от оси стержня со
стороны его сжатых волокон (рис.12, б)
и соединяем полученные точки прямой линией (равномерно
распределенной нагрузки нет!).
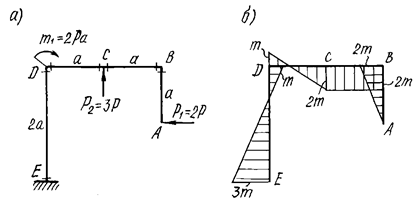
Рис. 12.
Расчетная схема рамы и эпюра изгибающих моментов
Стержень BD имеет два участка
- BC и СD. Вычисляются изгибающие моменты в
сечениях B, C, D.
В сечении В изгибающий момент MB = 2Pa, так как при переходе через узел величина изгибающего
момента не изменяется, сжатые волокна стержня располагаются снизу.
В сечениях С и D
изгибающие моменты MC = P1∙a = 2P∙a; MD = P1∙a – P2∙a = 2P∙a-3P∙a = -P∙a.
В
последнем выражении момент, зависящий от силы P1, условно принят положительным.
При этом сжатые волокна стержня BD
располагается снизу от его оси.
Момент от силы P2 в этом случае отрицателен, так как от действия силы
P2 волокна, расположенные снизу,
растягиваются. Отрицательное значение изгибающего момента в сечении D, означает, что сжатое волокно теперь
располагается теперь не снизу,
а сверху от оси стержня. Очевидно, что эпюра М на участке BD
ограничена прямыми линиями.
Стержень DE имеет только один
участок, в начале которого (сечение D)
приложена пара сил с моментом 2Pa. Изгибающий момент в сечении D стержня DE
MD = P1∙a – P2∙a + m1 = 2P∙a - 3P∙a + 2P∙a = P∙a.
Найденное значение откладываем справа
от оси стержня DE, так как от действия
силы P1 сжатые волокна расположены справа, и перед первым слагаемым в выражении для вычисления
изгибающего момента поставлен знак плюс, что означает сжатие волокон справа от действия всех внешних сил,
приложенных к раме.
Изгибающий момент в сечении E
ME = P1∙a + P2∙a – m1 = 2P∙a + 3P∙a - 2P∙a = 3P∙a.
Здесь знак (плюс или минус) перед каждым слагаемым выбран в
соответствии с введенным ранее правилом.
По найденным значениям изгибающих моментов для стержня DE построена эпюра М, ограниченная прямой линией.
Эпюра изгибающих моментов для всей рамы показана на рис.12,б. Здесь, как и раньше, использовано обозначение m=Pa.
Пример 3
Используя метод “характерных” сечений, построить
эпюры распределения поперечных сил Q, изгибающих моментов M и продольных сил N для статически
определимой рамы, изображенной на рис. 13.
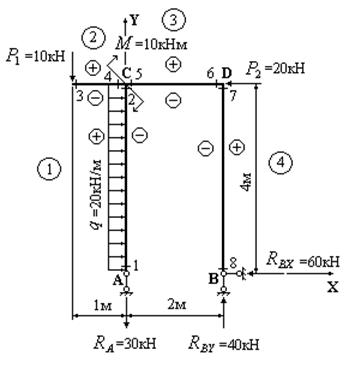
Рис. 13
Решение.
1. Определяем опорные реакции:
ΣX=q∙4 - P2 - RBX =
0; (а)
ΣMA=P1∙1
- q∙4∙2 – M + P2∙4
+ RBY∙2 = 0; (б)
ΣMB=P1∙3
- q∙4∙2 – M + P2∙4
+ RA∙2 = 0; (в)
Из уравнения (а) находим реакцию RBX:
RBX = q∙4 - P2 = 80-20 = 60 кН.
Из уравнения (б) находим реакцию RBY:
![]()
Из уравнения (в) находим реакцию RA:
![]()
Реакции получились положительными. Следовательно, их
направления выбраны верно.
Выполним проверку. Для этого составим сумму проекций
всех сил на ось Oy.
Эта сумма должна тождественно равняться нулю:
ΣY= -P1 – RA + RAY =
-10 – 30 +40 = 0.
2. Расставляем реакции, разбиваем раму на участки,
выбираем точку наблюдения, расставляем знаки на каждом участке для поперечных
сил и изгибающих моментов и расставляем номера “характерных” сечений таким
образом, чтобы нумерация сечений производилась слева направо. При этом знак «+»
должен находиться над участком, знак «-» – под участком.
3. Определяем значения поперечных сил в “характерных”
сечениях рамы:
Q1 =
0; Q2 = -q∙4 = -80 кН; Q3 = -P1 = -10
кН; Q4 = -P1 = -10
кН;
Q5 = -RBY =
-40 кН; Q6 = -RBY =
-40 кН; Q7 = RBx =
60 кН; Q8 = RBX =
60 кН.
Строим эпюру поперечных сил (рис.14):
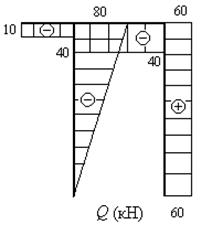
Рис.14
4. Определяем значения для изгибающих моментов в “характерных” сечениях
рамы:
M1 =
0; M2 = -q∙4∙2 = -160 кНм; M3 =
0; M4 = -P1∙1
= -10 кНм;
M5 = -RBY∙2 - RBX∙4
= 40∙2 - 60∙4 = -160 кНм; M6 = -RBX∙4 = -240 кНм;
M7 = -RBX∙4 = -240 кНм; M8 = 0.
Строим эпюру изгибающего момента (рис.15):
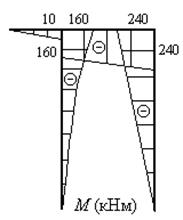
Рис.15
5. Выполняем статическую проверку. Статическая проверка состоит а кинематической проверке расновесия
узлов рамы. Вырежем сечениями №2, №4 и №5 первый узел С
и изобразим его на рис. 16,а.
Приложим к узлу моменты, характеризующие влияние отброшенной части рамы на
узел. Эти моменты численно равны значениям изгибающих моментов соответственно в
сечениях №2, №4 и №5. Направление действия этих моментов определяется правилом
знаков для изгибающего момента. Значения моментов на рис. 16 приведены в кНм.
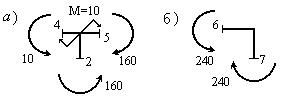
Рис.16
Рассматривая равновесие узла С, выделенного из
рамы сечениями №2, №4 и №5, составляем уравнение для суммы моментов
относительно центра узла. В данном случае следует учитывать, что на узел С действует внешний заданный момент М.
ΣM = -10 +10 - 160 +160 = 0. (а)
Как видно из уравнения (а) узел С находится в
равновесии. Выполним проверку узла D,
выделенного из рамы сечениями №6 и №7 (рис.15,б). Составим сумму моментов,
действующих на узел D:
ΣM
= -240 + 240 = 0. (б)
Как видно из уравнения (б) узел D также находится в равновесии.
6. Определяем величину продольной силы в стержнях рамы. Для этого
вырежем сечениями №2, №4 и №5 узел C и
изобразим его на рис. 16,а. Приложим
к узлу C продольные
усилия N и поперечные силы Q, характеризующие влияние отброшенной части рамы на узел.
Эти усилия численно равны значениям соответственно продольных и поперечных сил
в сечениях №2, №4 и №5. Направление действия этих усилий определяется правилом
знаков для продолных усилий и поперечных сил.
Значения поперечных сил на рис.17 приведены в кН.
Составим суммы проекций сил, приложенных к узлу C, на оси Ox и Oy:
ΣX= -N4 + N5 + Q2 = 0; (в)
ΣY= -N2 – Q4 + Q5 =
0. (г)
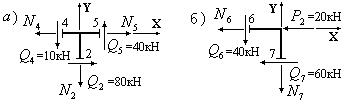
Рис.17
Рассматривая уравнение (в), обнаруживаем, что в этом уравнении две
неизвестных продольных силы N4 и N5. Решить это уравнение относительно усилий N4 и N5
невозможно. Найдем сначала усилие N4, рассмотрев равновесие участка рамы, ограниченного
сечениями №3 и №4 (рис.18).

Рис.18
Составим для изображенного на рис.18 стержня условие равновесия
приложенных к стержню сил, на ось Ox:
ΣX= -N3 + N4 = 0, (д)
откуда N4=N3.
Но усилие N3 = 0, так как в сечение №3 отсутствуют силы,
действующие вдоль участка стержня 3-4
(рис.13). Следовательно, усилие N4 = 0.
Теперь можно определить остальные продольные усилия, действующие в узле C. Из уравнения (в) находим:
N5 = -Q2 = -80 кН.
Из уравнения (г) найдем усилие N2:
N2 = -Q4 + Q5 = -10 +
40 =30 кН.
Найдем продольные усилия в сечениях №6 и №7. Для этого составим
уравнения равновесия сил, приложенных к узлу D на горизонтальную и вертикальную оси координат Х и Y (рис.17,б). При составлении этих уравнений не следует
забывать, что к узлу D приложена сосредоточенная сила P2.
ΣX= -N6 – P2 – Q7 = 0; (е)
ΣY= -N7 – Q6 =
0. (ж)
Из уравнения (е) находим продольную силу в сечении №6:
N6 = P2 – Q7 = -20 -
60 = -80 кН.
Из уравнения (ж) находим продольную силу в сечении №7:
N7 = -Q6 = -40 кН.
Откладываем найденные значения для продольной силы и строим эпюру продольных усилий ![]() (рис.19).
(рис.19).
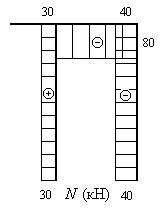
Рис.19
Приведенный пример построения эпюр поперечных сил и изгибающих моментов
для балок и эпюр поперечных сил, изгибающих моментов и
продольных усилий для рам позволяют получить наглядное представление о
преимуществах и недостатках метода “характерных” сечений. К числу преимуществ
этого метода можно отнести простоту определения внутренних силовых факторов. К
числу недостатков – отсутствие аналитических законов распределения внутренних
силовых факторов по длине элементов конструкции. Однако, использования
дифференциальных зависимостей между интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом для анализа поведения распределения
внутренних усилий и следствий из них в значительной мере компенсирует последний
недостаток. Сделанный вывод позволяет рекомендовать метод построения эпюр
распределения внутренних силовых факторов по “характерным’ сечениям в учебную
практику.
Пример 4
Для рамы, изображенной на
рис.20, требуется построить эпюры внутренних силовых факторов, если F = 50 кН, q =
20 кН/м, М = 60 кН/м.
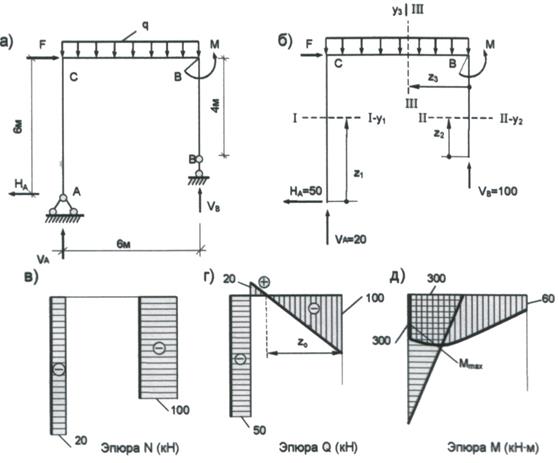
Рис.20. а) расчетная схема рамы; б) объект
равновесия; в) эпюра продольных сил;
г)эпюра
поперечных сил; д) эпюра изгибающих
моментов
Решение.
Выделяем объект равновесия для
этого, отбрасываем опорные связи, а действие опорных связей заменяем опорными
реакциями в этих связях (рис.20, б). Для
определения опорных реакций для этой рамы используются уравнения равновесия. Мы
не будем подробно останавливаться на этом, а величины найденных опорных реакций
укажем на рис.20,б.
Особенностью построения эпюр
в рамах является то, что в поперечных сечениях рамы могут одновременно
возникать три внутренних силовых фактора - Mx, Qy, и Nz. Одни и те же
внешние силы на разных участках могут вызывать разные внутренние силовые
факторы. В рамах выбирают текущую систему координат. На каждом участке ось
элемента будем совмещать с осью z, а
оси x и y располагаем в плоскости нормального сечения. В раме
дополнительными, характерными точками, являются узлы рамы.
Разбиваем ось рамы на
участки. Тогда всего участков три - АС, СD, BD. Будем
строить три эпюры одновременно
Рассматриваем участок AС. Рассекаем брус сечением I-I на расстоянии z1 от опоры А, 0≤z1≤6м (рис.20,
б). Отбрасываем
правую часть и рассматриваем равновесие левой оставленной части.
Составляем уравнение для
определения внутренних силовых факторов в сечении I-I.
Nz1 = ΣFzлев; Nz1 = -VA; Nz1 = -20 кН.
Qy1 = ΣFyлев; Qy1 = HA; Qy1 = 50 кН;
Mx1 = Σmxлев; Mx1 = HA∙z1;
Mx1 = 50∙z1.
Знаки усилий приняты в
соответствие с принятым правилом знаков. Nz – отрицательна так
как VA сжимает отсеченную
часть, а Qy1 –
отрицательна, так как НA
стремится повернуть отсеченную часть против часовой стрелки. При
определении знака изгибающего момента условно будем считать, если внешние силы
изгибают отсеченную часть выпуклостью внутрь контура рамы, то изгибающий момент
положительный. В нашем случае, если мысленно закрепить сечение I-I, НA будет изгибать отсеченную часть выпуклостью
внутрь контура.
Из уравнения видно, что
продольная сила на участке АС –
постоянна, поперечная сила – постоянна, а изгибающий момент изменяется по
линейному закону.
Вычисляем два значения MxI:
при zI=
0, Mx1 = 0;
при zI
= 6 м, MxI = 300 кНм.
Рассматриваем участок BD. Рассекаем раму сечением II-II, отбрасываем левую часть и
рассматриваем равновесие правой оставленной части (рис. 19, б). Определяем внутренние силовые факторы в сечении II- II на расстоянии z2 от опоры
В, 0≤z2≤4м.
NzII = ΣFzправ;
Nz1I = -VB;
Nz1 = -100 кН.
QyI1 = ΣFyправ; QyI1 = 0;
MxI1 = Σmxправ; MxI1 = 0.
Из уравнений видно, что поперечная
сила и изгибающий момент на всем протяжении участка равны
нулю, а продольная сила постоянна и отрицательна, т.к. VB – сжимает отсеченную часть.
Рассматриваем участок CD. Рассекаем брус сечением III-III, отбрасываем левую часть и рассматриваем равновесие правой
оставленной части (рис.20, б). Определяем внутренние силовые факторы в сечении III- III
на расстоянии z3 от узла D, 0≤z3≤6 м.
Составляем уравнения для
определения внутренних силовых факторов в сечении III-III в соответствие с принятым правилом знаков.
NzII1 = ΣFzправ; NzIII = -0;
QyII1 = ΣFyправ; QyII1 = -VВ + q×z3; QyII1 = -100 + 20∙z3;
MxII1 = Σmxправ; MxII1 = VA∙z3 + М - (q∙z3)2/2 MxII1 = 100∙z3 + 60 - 10∙z32.
Из уравнения видно, что продольная
сила на всем протяжении участка равна нулю, Поперечная сила изменяется по
линейному закону. Знаки в уравнении ее членов, взяты из следующих соображений:
первый член отрицательный, т.к. VВ
вращает отсеченную часть относительно сечения против часовой стрелки, второй член положительный, т.к.
распределенная нагрузка q вращает по
часовой стрелке.
Изгибающий момент изменяется
по закону квадратной параболы. Так как под действием VB и M отсеченная
часть мысленно закрепленная в сечении изгибается
выпуклостью внутрь контура, то первый и второй член уравнения положительные, а
от действия распределенной нагрузки – выпуклостью наружу контура и знак третьего
члена уравнения отрицательный.
Вычисляем два значения Qy1II:
при z3 = 0, QyII1 = - 100 кН;
при z3 = 6 м, QyIII = 20 кН.
Вычисляем три значения MxIII:
при z3= 0, MxIII
= -60 кНм;
при z3 = z0 = 5м, MxIIImax = 310 кНм;
при z3 = 6м, MxIII
= 300 кНм.
MxIIImax при z3
= z0, определен согласно дифференциальной зависимости между
изгибающим моментом и поперечной силой. В том месте, где поперечная сила равна
нулю, эпюра изгибающих моментов имеет экстремум. Так как эпюра Qу на участке СD линейна, то из подобия треугольников,
нулевая точка О
лежит от начала участка на расстоянии z0
= 100 /20 =5м.
По найденным данным строим
эпюры Nz,
Qy
и Mx в раме. Для построения каждой из трех
эпюр тонкими линиями проводим контур рамы, который служит базовой линией эпюры (рис.20, в, г, д). Ординаты эпюры моментов
откладываем в сторону растянутых волокон.
Пример 5
Для
рамы, предоставленной на рис.21,а
построить эпюры поперечных сил и изгибающих моментов.

а)
б)
Рис. 21
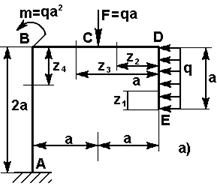
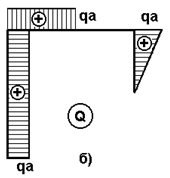
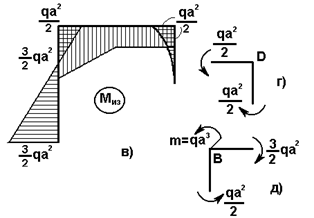
Рис.22
Решение.
В
статически определимых жестких рамах, заделанных одним концом, предварительное
определение опорных реакций необязательно. Построение эпюр в таких случаях можно вести от свободного конца. Рама имеет
четыре участка, для каждого из них составляем уравнение поперечных сил и
изгибающих моментов, соблюдая принятые ранее правила знаков.
1
участок: рассекаем участок на расстояние Z1 от свободного торца E
(рис.22,а).
Ординаты
изгибающего момента откладываем на сжатом волокне бруса, а знак момента
указывать не будем.
1
участок: 0≤Z1≤a Q = qZ1; ![]()
при
Z1 = 0 Q =
0; M = 0.
при
Z1 = a Q = qa; ![]()
2
участок: 0≤Z2≤a Q = 0; ![]()
3
участок: 0≤Z2≤2a Q = qa; ![]()
Оба
изгибающих момента берем с одним знаком, т.к. сжимают одно и то же (нижнее)
волокно.
при
Z3 = a ![]()
при
Z3 = 2a ![]()
4
участок: 0≤Z4≤2a Q = -qa; ![]()
В
этом уравнении для Миз со знаком плюс взят
момент, сжимающий правое волокно (момент от сосредоточенной силы F), а моменты,
сжимающие левое волокно бруса, взяты со знаком минус. Разумеется, что эпюра Миз не изменится, если знаки изгибающих моментов
в уравнении (*) поменять на противоположные.
при
Z4 = 0 ![]()
Получаем
момент со знаком плюс, т.е. сжато будет правое волокно бруса.
при
Z4 = 2a ![]() (сжато левое
волокно бруса)
(сжато левое
волокно бруса)
Окончательный
вид эпюр Q и Миз представлен
соответственно на рис.22,б и в.
Для
проверки правильности построения эпюры Миз,
можно использовать следующие положения: любой узел, вырезанный из наружной
рамы, должен находиться в равновесии под действием моментов, заменяющих
действие на него отброшенных элементов.
Так,
например, вырежем узел D рассмотренной рамы (рис.22,г)
Запишем
уравнение: ![]()
Вырежем
узел B (рис.22,д): ![]()
Таким
образом, условия равновесия узлов Д и В
удовлетворяются. Сечение А самое опасное, т.к. в нем
возникает самый большой Миз.
![]() (рис.22,в).
(рис.22,в).
Пример 6
Построить
эпюры поперечных сил и изгибающих моментов для рамы, представленной на рис.23,а.
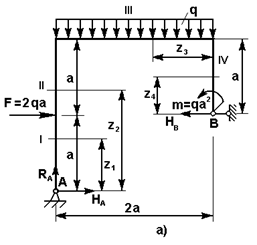
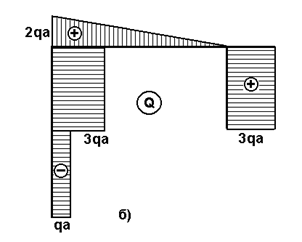
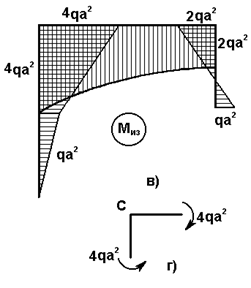
Рис.23
Решение.
Для
решения задачи необходимо предварительно, используя уравнение равновесия
статики, определить опорные реакции (рис.23,а):
ΣMA = 2qa2 + 2qa2 – qa2 - HB∙a = 0 HB=3qa.
ΣMB = RA∙2a + HA∙a – 2qa2
- qa2 = 0 (*)
Спроектируем
все силы на горизонтальную ось:
2qa = 3qa + HA =
0 HA=qa
Из
уравнения (*) получим: RA=2qa
Для
проверки запишем сумму проекций на вертикальную ось:
2qa – 2qa = 0
т.е.
реакции определены правильно.
Переходим
к построению эпюр.
Рама
имеет четыре участка нагружения.
1
участок: 0≤ Z1 ≤a.
Рассмотрим
равновесие отсеченной части длиной Z1. Из условия равновесия
следует: Q= -HА = -qa
М
= HA∙Z1,
при
Z1=0 М = 0,
при
Z1=a
М = qa2.
Сжатое
волокно на 1 участке - правое, поэтому строим эпюру на правом волокне 1-го
участка рамы.
2
участок: a≤
Z2 ≤2a.
рассмотрим
равновесие отсеченной части длиною Z2.
Q= -HA - F= -qa - 2qa = -3qa
М
= HA∙Z2 + F∙(Z2-a)
В
уравнении изгибающие моменты записаны с одинаковым знаком, т.к. оба момента
сжимают правое волокно рамы.
При
Z2=а
М = qa2
При
Z2=2a М = 4qa2.
3
участок: 0≤ Z3 ≤2a
Рассмотрим
равновесие части рамы, расположенной справа от сечения.
Q=qZ3
при
Z3=0 Q=0
при
Z3=2a Q=2qa
![]()
при Z3 = 0 M=2qa2
при Z3 = 2a M=4qa2.
Обе
ординаты изгибающих моментов откладываем вниз от осевой линии рамы, т.к.
сжатыми оказались нижние волокна рамы.
Изгибающий
момент меняется по закону квадратной параболы. Парабола обращения выпуклостью
вверх.
4
участок: 0≤
Z4 ≤2a
Рассмотрим
равновесие участка рамы длиною Z4
Q
= Hв =
3qa М =HB∙Z1-m=3qa∙Z4-qa2,
при
Z4=0 M = -qa2
этот момент сжимает правые волокна, поэтому откладываем ординату на правом
волокне,
при
Z4=a М = 2qa2 этот
момент сжимает левое волокно, поэтому на эпюре М ордината 2qa2
откладывается на левом волокне.
Эпюры
Q и М показаны на рис.23, б и в.
Построеные
эпюры всегда следует проверять с точки зрения соблюдения дифференциальных
зависимостей между q, Q и М. Кроме того, следует
проверять, соблюдается ли равновесие в узлах рамы. Например, вырезая узел С, прикладываем к вырезанной части внутренние силовые
факторы рис.23, г, возникающие в
указанных сечениях.
ΣMC = 4qa2 - 4qa2 =
0.
Если
к рассматриваемому узлу приложен внешний момент, то этот момент должен войти в
уравнение равновесия рассматриваемого узла. Опасное сечение С,
где max M = 4qa2.
Пример 7
На рисунке 24 изображена рама, состоящая из двух
частей, соединенных шарниром. Построить эпюры внутренних силовых факторов.

Рис. 24
Решение.
Изобразим отдельные части рамы и покажем приложенные к
ним силы (рис. 25)

Рис. 25
Для определения реакции шарнирно подвижной опоры А составим уравнение моментов относительно оси шарнира В.
ΣmB=0;
P∙BD - YA∙AC=0,
Или
1,5∙5-YA∙2,5=0 → YA=3 кН.
По уравнениям проекций на горизонтальную и
вертикальную ось найдем
XB=1,5 кН и YB=3 кН.
Найденные силы XB и YB выражают действие правой части конструкции на левую. Значит действие левой части
конструкции на правую выражается силами
![]()
Теперь можно приступать к построению эпюр.
Участок BL нагружен
равномерно распределенной нагрузкой. Значит вдоль
этого участка поперечная сила меняется по линейному закону, а изгибающий момент
- по закону параболы. Вдоль остальных участков поперечные силы неизменны, а
изгибающие моменты меняются линейно.
Участок АС
Qy=YA=3 кН; MA=0; MC=YA∙AC=3∙2,5=7,5
кНм,
Участок CD
Qy= -P= -1,5 кН; MD=0; MC= -P∙DC= -1,5∙3= -4,5 кНм,
Участок СВ
Qy= -P= -1,5 кН; MB=0, (сечение В примыкает к шарниру)
MC=XB∙BC=1,5∙2= 3 кНм.
Участок BL
QyB=![]() = 3 кН; QyL=
= 3 кН; QyL=![]() - q∙BL=3 - 2∙4 = -5 кН.
- q∙BL=3 - 2∙4 = -5 кН.
![]()
Участок LK
QK=![]() = 1,5 кН;
= 1,5 кН;
![]()
![]()
Построив эпюру поперечной силы (рис. 26), найдем
сечение стержня BL, в котором поперечная сила
равна нулю. Его положение определим расстоянием z1. На
основании формулы
![]()
Изгибающий момент в этом сечении
![]()

Рис. 26
На рисунке 27 изображена эпюра Mx, построенная по результатам вычислений.

Рис. 27
Продольная сила.
Участки АС и DC от
продольных нагрузок свободны, а участок СВ сжимается
силами YA и YB.
Так что продольная сила определяется или силой YA или
силой YB
Nz= -YA= -YB= -3 кН.
Учаcток BL сжимается силой ![]() .
.
Nz= -![]() = -1,5 кН.
= -1,5 кН.
Участок LK растягивается силой ![]() и сжимается
распределенной нагрузкой.
и сжимается
распределенной нагрузкой.
Nz= -![]() - q∙BL = 3 - 4∙2= -5 кН.
- q∙BL = 3 - 4∙2= -5 кН.
Эпюра продольной силы изображена на рис. 28.

Рис. 28
Для статической проверки вырежем узел С и изобразим
силовые факторы в примыкающих к нему сечениях (рис. 29).

Рис. 29
Пример 8
Для
статически определимой рамы (рис.30) требуется:
1) Определить реакции опор;
2)
Написать аналитические выражения для внутренних силовых факторов (нормальной
силы N, поперечной силы Q и изгибающего
момента M) для каждого участка рамы в принятых локальных
системах координат;
3)
Построить эпюры N, Q и M;
4)
Определить опасное сечение, где изгибающий момент имеет максимальное (по
абсолютной величине) значение.
Дано: ![]()
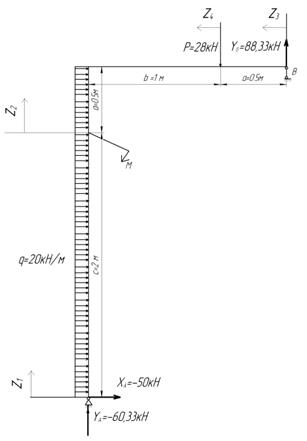
Рис.30
Решение.
1.
Отбросим опоры и заменим их влияние на раму опорными
реакциями (рис.30).
Составим
сумму моментов всех сил:
ΣX= -XA + q∙(a+c) = 0.
XA = q∙(a+c) = 20∙(0,5+2) = -50 кН.
![]()
![]()
![]()

Проверка
реакций:
Составим
сумму проекций всех сил отрезка BC на
вертикальную ось Y:
ΣY = -YB + YC – P – q∙b = -60,33 – 28 +88,33 = 0.
0
= 0.
Полученное
тождество показывает, что реакции вычислены правильно.
2.
Построим эпюры N, Q и M.
Балка
имеет четыре участка. Используя метод сечений, составляем аналитические
выражения для N, Q и M.
I участок ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
II участок ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III участок ![]()
![]()
![]()
![]()
![]()
![]()
IV участок ![]()
![]()
![]()
![]()
![]()
![]()
Эпюры
N, Q и M показаны на рис. 31.
Из
эпюры M следует, что в опасном сечении балки Mmax=104,5 кНм.
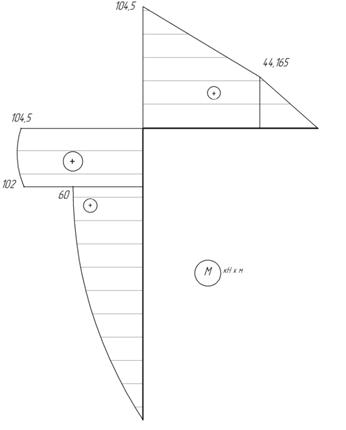
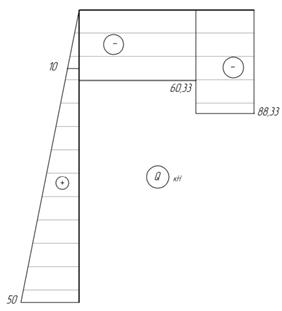
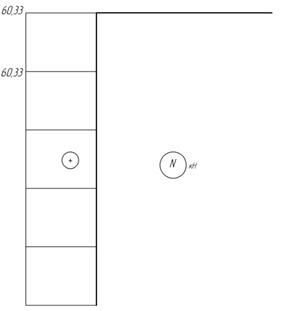
Рис.31
Пример 9
Для
статически определимой рамы (рис.32) требуется:
1) Определить реакции опор;
2)
Написать аналитические выражения для внутренних силовых факторов (нормальной
силы N, поперечной силы Q и изгибающего момента M) для каждого участка рамы в принятых локальных
системах координат;
3)
Построить эпюры N, Q и M;
4)
Определить опасное сечение, где изгибающий момент имеет максимальное (по
абсолютной величине) значение.
Дано: ![]()
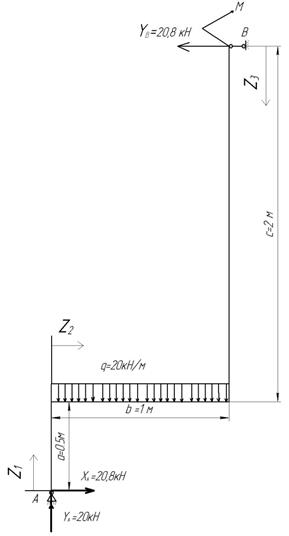
Рис.32
Решение.
1. Отбросим опоры и заменим их влияние на раму опорными реакциями (рис.32).
Составим сумму моментов всех сил:
![]()
![]()
![]()
![]()
ΣX = XA – YB = 0
XA = YB = 20,8 кН.
Проверка реакций:
Составим сумму проекций всех сил на ось Y:
ΣY = YA – q∙b = 20 - 20∙1 = 0.
0 = 0.
Полученное тождество показывает, что реакции вычислены правильно.
2. Построим эпюры N, Q и M.
Балка имеет три участка. Используя метод сечений, составляем аналитические выражения для N, Q и M.
I участок ![]()
![]()
![]()
![]()
![]()
![]()
II участок ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III участок ![]()
![]()
![]()
![]()
![]()
![]()
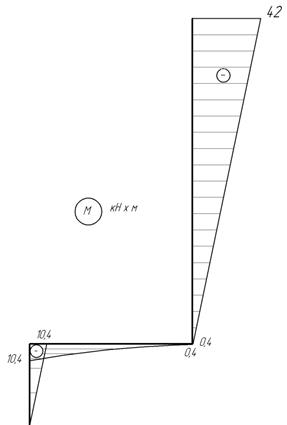
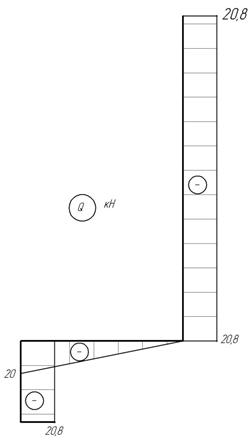
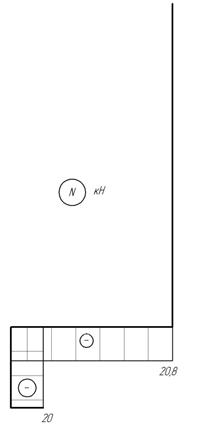
Эпюры N, Q и M показаны на рис. 33.
Из
эпюр M следует, что в опасном сечении балки Mmax=42 кНм.
Рис. 33
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов