Расчетно-графические работы

Главная

Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии

Для стального стержня круглого поперечного сечения диаметром D (рис.1) требуется:

1) построить эпюры продольной силы;

2) определить грузоподъемность стержня, если [σ] = 240 МПа;

3) определить полное удлинение стержня, если Е = 2∙10⁵ МПа.

Данные взять из табл.1.

Таблица 1

Номер cтроки	Схема по рис.1	D, м	а, м	b, м	F, кН
01	1	0,01	1	1,1	12
02	2	0,02	2	1,2	10
03	3	0,03	3	1,3	12
04	4	0,04	3	1,4	6
05	5	0,05	2	1,5	8
06	6	0,06	1	1,6	10
07	7	0,07	2	1,7	6
08	8	0,08	3	1,8	8
09	9	0,09	1	1,9	6
10	10	0,1	1	1,0	12
11	11	0,01	2	1,1	12
12	12	0,02	3	1,2	10
13	13	0,03	2	1,3	12
14	14	0,04	1	1,4	6
15	15	0,05	2	1,5	8
16	16	0,06	3	1,6	10
17	17	0,07	1	1,7	6
18	18	0,08	2	1,8	8
19	19	0,09	3	1,9	6
20	20	0,1	1	1,0	12
21	21	0,01	1	1,1	12
22	22	0,02	2	1,2	10
23	23	0,03	3	1,3	12
24	24	0,04	4	1,4	6
25	25	0,05	1	1,5	8
26	26	0,06	2	1,6	10
27	27	0,07	3	1,7	6
28	28	0,08	4	1,8	8
29	29	0,09	1	1,9	6
30	30	0,1	2	1,0	12
31	31	0,01	3	1,4	12
32	32	0,02	4	1,5	6
33	33	0,03	1	1,6	8
34	34	0,04	2	1,7	10
35	35	0,05	3	1,8	6
36	36	0,06	4	1,9	8
	в	г	б	а	а

1 схема 2 схема 3 схема 4 схема

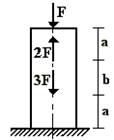
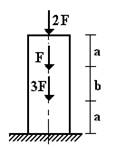
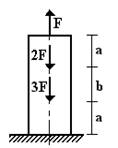
5 схема 6 схема 7 схема 8 схема

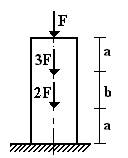
9 схема 10 схема 11 схема 12 схема

13 схема 14 схема 15 схема 16 схема

17 схема 18 схема 19 схема 20 схема

21 схема 22 схема 23 схема 24 схема

25 схема 26 схема 27 схема 28 схема

29 схема 30 схема 31 схема 32 схема

33 схема 34 схема 35 схема 36 схема

Рис.1

Задача 2. Расчет стержней постоянного поперечного сечения при растяжении-сжатии с распределенной нагрузкой

Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q₁ и q₂ и сосредоточенными силами F₁ и F₂. Построить эпюру нормальной силы.

Данные взять из табл.2 и рис.2.

Таблица 2

Номер cтроки	Схема по рис.2	F₁/ql	F₂/ql	q₁/q	q₂/q	l₁/l	l₂/l
01	I	–1,0	2,0	–1,0	1,0	1,0	2,0
02	II	2,5	–2,5	2,0	–2,0	1,5	1,5
03	III	–2,0	1,0	1,0	–2,0	2,0	2,5
04	IV	1,5	–1,5	–2,0	1,0	2,5	1,0
05	V	–1,0	3,0	1,0	2,0	3,0	1,0
06	VI	1,5	–2,0	–1,0	2,0	2,0	1,5
07	VII	–2,0	1,5	2,0	–1,0	2,5	2,5
08	VIII	3,0	–1,0	–2,0	–1,0	1,0	2,0
09	IX	–1,5	2,0	–1,0	1,0	1,5	1,5
10	X	2,0	–3,0	1,0	2,0	2,0	1,0
11	I	–1,0	2,0	–1,0	1,0	1,0	2,0
12	II	2,5	–2,5	2,0	–2,0	1,5	1,5
13	III	–2,0	1,0	1,0	–2,0	2,0	2,5
14	IV	1,5	–1,5	–2,0	1,0	2,5	1,0
15	V	–1,0	3,0	1,0	2,0	3,0	1,0
16	VI	1,5	–2,0	–1,0	2,0	2,0	1,5
17	VII	–2,0	1,5	2,0	–1,0	2,5	2,5
18	VIII	3,0	–1,0	–2,0	–1,0	1,0	2,0
19	IX	–1,5	2,0	–1,0	1,0	1,5	1,5
20	X	2,0	–3,0	1,0	2,0	2,0	1,0
21	I	–1,0	2,0	–1,0	1,0	1,0	2,0
22	II	2,5	–2,5	2,0	–2,0	1,5	1,5
23	III	–2,0	1,0	1,0	–2,0	2,0	2,5
24	IV	1,5	–1,5	–2,0	1,0	2,5	1,0
25	V	–1,0	3,0	1,0	2,0	3,0	1,0
26	VI	1,5	–2,0	–1,0	2,0	2,0	1,5
27	VII	–2,0	1,5	2,0	–1,0	2,5	2,5
28	VIII	3,0	–1,0	–2,0	–1,0	1,0	2,0
29	IX	–1,5	2,0	–1,0	1,0	1,5	1,5
30	X	2,0	–3,0	1,0	2,0	2,0	1,0
31	I	–1,0	2,0	–1,0	1,0	1,0	2,0
32	II	2,5	–2,5	2,0	–2,0	1,5	1,5
33	III	–2,0	1,0	1,0	–2,0	2,0	2,5
34	IV	1,5	–1,5	–2,0	1,0	2,5	1,0
35	V	–1,0	3,0	1,0	2,0	3,0	1,0
36	VI	1,5	–2,0	–1,0	2,0	2,0	1,5
	а	г	б	а	в	б	г

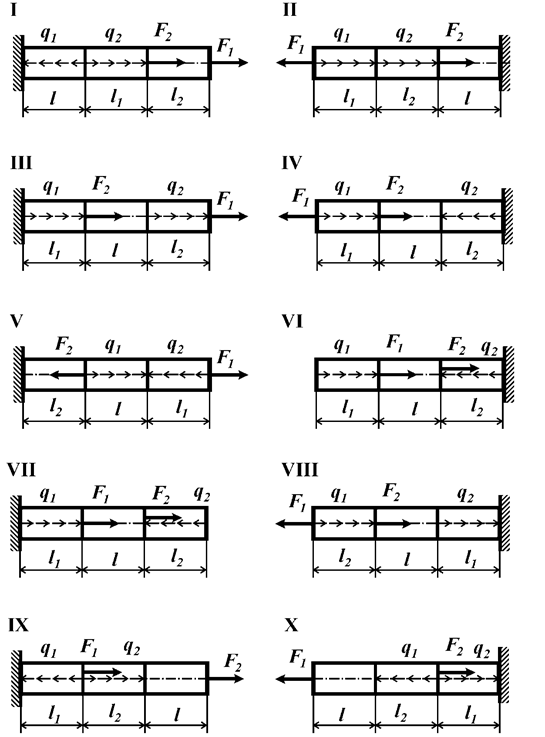
Рис.2

Задача 3. Расчет стержней постоянного поперечного сечения при растяжении-сжатии с распределенной нагрузкой

Для прямого стержня, нагруженного осевыми продольными нагрузками, необходимо:

1. Записать выражение продольной силы N(z) и построить её график.

2. Определить размер r квадратного поперечного сечения из расчёта на прочность, округлив его до ближайшего из нормального ряда.

3. Для стержня выбранного размера вычислить нормальные напряжения в опасном сечении.

4. Определить наибольшее касательное напряжение в этом стержне и указать, в каком сечении оно действует, найти нормальное напряжение в этом стержне.

5. Вычислить главные линейные деформации в точках опасного поперечного сечения.

6. Найти размеры этого сечения после деформации.

Данные взять из табл.3 и рис.3.

Рис. 3

Таблица 3

Номер cтроки	l, м	a, м	b, м	с, м	d, м	P₁, кН	P₂, кН	q, кН/м	[σ], МПа
01	2,1	0	0,6	0,1	1,8	20	35	- 66	108
02	2,5	0	0,4	0,4	1,4	46	- 25	85	102
03	2,4	0,2	0,8	0	1,2	50	- 90	69	115
04	2,5	0	0,8	0,2	1,8	51	80	- 40	120
05	2,2	0	1,4	0,6	2	10	- 49	62	122
06	2	1,6	1,4	0	1	-25	- 19	61	119
07	2	0,7	1,6	0	1,2	51	- 91	59	159
08	2,5	0	1,8	1	1,4	-45	15	51	134
09	2,4	0,6	1,6	0	1,2	-28	14	61	103
10	2,5	0	2,1	1	2,5	-79	62	81	105
11	2,5	1,8	1,3	0	0,9	-57	- 33	69	154
12	2,1	0	1,4	0,7	1,9	- 52	30	59	126
13	2,5	0	1,2	1	2	19	- 59	68	104
14	2,4	0,5	1,5	0	0,9	- 48	27	63	138
15	2,4	0	1,4	0,8	2,2	19	- 68	44	124
16	2,4	0,6	1,3	0	1,6	22	- 27	22	121
17	2,2	0,9	1,8	0	1,2	42	23	- 32	120
18	2,3	0	1,7	0,9	1,9	15	- 49	50	170
19	2,1	0,6	1,4	0	1,9	25	- 85	63	114
20	2,5	0	1,6	1,1	2,5	10	40	- 53	109
21	2,3	0,7	0	0,4	2,3	- 35	- 18	40	102
22	2,2	0	0,5	1	2	15	- 36	69	165
23	2,5	0,8	2,2	0	1,7	- 70	22	68	138
24	2,1	0	0,7	1,3	1,8	- 52	40	57	164
25	2,3	0,9	0,3	0	1,8	- 79	26	79	183
26	2,3	0	0,9	1,5	2,3	- 50	- 30	64	109
27	2,5	0,5	2,2	0	1,4	- 58	36	70	165
28	2,2	0	16	0,5	2,1	30	-50	96	198
29	2	0,5	1,6	0	1,1	- 40	72	- 82	191
30	2	0	0,9	0,3	1,5	18	- 67	63	177
31	2,5	1,8	1,3	0	0,9	-57	- 33	69	154
32	2,1	0	1,4	0,7	1,9	- 52	30	59	126
33	2,5	0	1,2	1	2	19	- 59	68	104
34	2,4	0,5	1,5	0	0,9	- 48	27	63	138
35	2,4	0	1,4	0,8	2,2	19	- 68	44	124
36	2,4	0,6	1,3	0	1,6	22	- 27	22	121
	г	б	а	а	в	г	а	б	г

Примеры выполнения задач

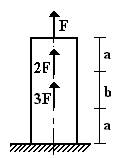
Пример 1

На рис. 4,а представлена схема бруса, нагруженного осевыми силами.

Требуется:

1) построить эпюру продольной силы;

2) построить эпюру перемещений.

Рис.4

Решение.

Для контроля правильности расчета продольных сил определим реакцию R в заделке, направив ее на растяжение по отношению к брусу. Используя уравнение равновесия и выбрав положительное направление продольной оси бруса Z, получим

ΣZ=0; R+3F-2F+F=0; R=-2F. (1)

Минус в ответе означает, что реакция направлена не на растяжение, как мы выбрали, а на сжатие.

Для определения продольных сил применим метод сечений.

1. Разбиваем брус на силовые участки I, II, III. Проводим на каждом участке произвольные поперечные сечения и отбрасываем части бруса.

2. Заменяем действие отброшенных частей бруса на каждом участке неизвестными продольными силами N₁, N₂, N₃, направив их от сечений, т.е. на растяжение (рис. 4, б, в, г).

3. Для каждого из участков составляем уравнение равновесия:

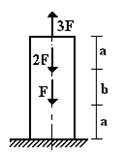
Участок I (рис. 4, б) ΣZ=0; N₁+F=0; N₁=-F;

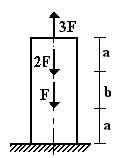
Участок II (рис. 4, в) ΣZ=0; N₂-2F+F=0; N₂=F; (2)

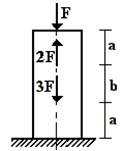
Участок III (рис. 4, г) ΣZ=0; -N₃+R=0; N₃=-2F.

Отсюда имеем N_i=ΣF_i, (3)

т.е. продольная сила N в произвольном сечении бруса численно равна алгебраической сумме проекций на продольную ось всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.

Это вывод позволит нам в дальнейшем определять продольные силы N без использования описанной процедуры составления уравнений равновесия. Так, например, согласно (3) для участка II получаем

N₂=-F+2F=F.

4. По полученным данным строим график распределения продольных сил по длине бруса – эпюру продольных сил (рис. 4, д). Для построения эпюры проводим базовую линию (ось бруса) и, выбрав масштаб, откладываем на каждом участке величины продольных сил. Т.к. на схемах рис. 4, б, в, г продольные силы были направлены на растяжение, то знаки в ответах поле решений уравнений равновесия (2) указывают: (+) – растяжение, (–) – сжатие. На эпюрах проставляют значения найденных продольных сил, их знак и наносят штриховку перпендикулярно оси бруса.

Из анализа эпюры N вытекает следующее правило ее проверки: в поперечных сечениях бруса, в которых приложены внешние активные (F) или реактивные (R) силы, на эпюре продольных сил возникают скачки, равные по величине этим нагрузкам.

Определим полную абсолютную деформацию бруса, показанного на рис. 4, а. Зная продольные силы N₁, N₂, N₃, согласно (2) с учетом формулы получим:

Построенные эпюры перемещений δ сечений бруса производят от заделки (или от любого конца, если брус не защемлен):

Выбирают масштаб и откладывают перемещения каждой точки (сечения) с учетом знаков. Полученную эпюру штрихуют (рис. 4, ж). Анализируя (4), видим, что перемещение любого поперечного сечения бруса численно равно удлинению (укорочению) части бруса, расположенного между заделкой и этим сечением. Например, перемещение сечения d равно:

Перемещение сечения d показано на эпюре δ (рис. 4, ж).

Пример 2

Для стержня из стали 30Х, площадью поперечного сечения А=8 см², представленного на рис. 5, требуется:

1) построить эпюру продольных сил;

2) построить эпюру осевых перемещений;

3) выполнить расчет на жесткость.

Рис.5

Решение.

1) Построение эпюр продольных сил и перемещений.

Построение эпюры продольных сил. Направим вдоль оси стержня ось z (рис.1.5). Составим уравнение равновесия системы:

Разобьем стержень на 3 участка АВ, ВС и CD, проведем на каждом из них произвольные сечения 1-1, 2-2, 3-3 с заданными координатами этих сечений z₁, z₂, z₃.

Участок АВ (0z₁l₁):

Участок ВС (0z₂l₂):

На участке DC (0z₃l₃) отбросим левую часть, ее действие заменим продольной силой N₃:

По полученным данным строим эпюру ЭN (рис. 5).

Построение эпюры перемещений. Запишем уравнения для перемещений w(z) сечений, считая площади сечений известными:

где w₀ – перемещение в начале участка, определяемое начальными условиями; l(z) – удлинение участка (абсолютная деформация участка стержня).

Если продольная сила N(z) зависит от координат сечения z, то:

Для стали 30Х МПа. В расчетах примем жесткость сечения при растяжении-сжатии кН.

Рассмотрим участок АВ (0z₁l₁):

Функция w(z₁) – квадратичная парабола. Так как в сечении А – заделка, то w₀=0 и w₁=0,0026 мм. Так как в пределах участка АВ продольная сила N₁ не меняет знака, то парабола в пределах участка не имеет экстремума.

Участок ВС (0z₂l₂):

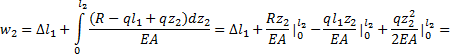
Функция w(z₂) – квадратичная парабола. Так как в пределах участка ВС продольная сила N₂ не меняет знака, то парабола в пределах участка не имеет экстремума.

На участке DC (0z₃l₃):