Главная

Лекция 6 (продолжение). Примеры решения на плоский изгиб

Определение напряжений и проверка прочности балок при плоском поперечном изгибе

Если Вы научились строить эпюры Q и М, то можете приступать к проверке прочности балок. Задача о проверке прочности балки чаще всего сводится к решению двух вопросов:

1) подбору сечения балки, т.е. определению таких минимальных размеров поперечного сечения, которые удовлетворяют условиям прочности в опасных точках;

2) определению грузоподъемности балки, т.е. нахождению такой максимальной нагрузки (допускаемой нагрузки) на балку, при которой удовлетворяются условия прочности во всех опасных точках.

Рассмотрим примеры проверки прочности балок круглого или прямоугольного сечений, двутавровых балок и балок произвольного моносимметричного сечения.

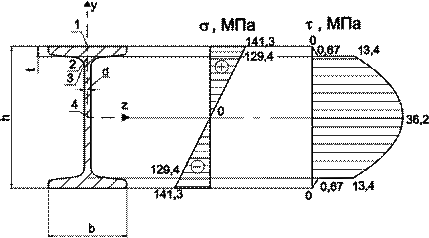
Пример 1.

Определить максимальное нормальное напряжение и максимальное касательное напряжение , возникающие в поперечных сечениях балки, представленной на рисунке. Принять h = 10 см, b = 6 см, l = 4 м, F = 8 кН.

Решение.

Из эпюры изгибающих моментов М определяем, что M_max =Fl/4 =8 кНм. Осевой момент сопротивления W_z для прямоугольного сечения определяется по формуле

Используя формулу расчета напряжений при изгибе, находим

На рис. б показана эпюра нормальных напряжений .

Из эпюры поперечных сил (рис. а) находим Q_max = F/2 = 4 кН. Далее определяем осевой момент инерции для прямоугольного сечения

и статический момент отсеченной части поперечного сечения (рис. б)

По формуле находим

Последняя формула показывает, максимальное значение касательного напряжения будет в точках поперечного сечения, расположенных на оси z, т.е. На рис. б показана эпюра касательных напряжений .

Пример 2.

Определить необходимую ширину b балки прямоугольного поперечного сечения (рис. а), причем h = 3b. Длина балки l= 4 м, F = 6 кН. Материал балки – сталь с R_y = 240 МПа, = 1.

Решение.

Согласно условию задачи, имеем M_max = Fl/4 = 6 кНм в сечении В. Вычисляем для прямоугольного поперечного сечения (см. рис.): W_z = b(3b)²/6 = 1,5b³, тогда из формулы получаем

W_zn,min = M_z,_max /( R_y) = 0,006/240 = 0,000025 м³ = 25 см³, но W_z = 1,5b³.

Приравнивая W_zn,min = W_z , определяем b = 2,55 см.

Пример 3.

Определить допускаемый минимальный диаметр d консольной балки (см. рис.) из стали с R_y = 240 МПа. Принять, что F = 1 кН, l = 1м, =1. Собственный вес балки не учитывать.

Решение.

Для сплошного круглого поперечного сечения имеем , где r – радиус поперечного сечения балки. Максимальный изгибающий момент будет в заделке В: M_max = M_B = F2l + Fl = 3lF = 3 кНм.

Из формулы находим момент сопротивления сечения

W_zn,min = M_max /( R_y) == м³.

Приравнивая W_zn,min = W_z, находим r = 0,025 м = 2,5 см или d = 5 см.

Пример 4.

Для заданной расчетной схемы двухопорной балки (см. рис.) построить эпюры поперечных сил и изгибающих моментов и подобрать стальную балку двутаврового поперечного сечения, если P= 20 кн =2 т, М =20 кНм =2 тм, q=1,5 кН/м =1,5 т/м, = 1 м, = 2 м, l = 4 м, =160 МПа =1600 кг/см².

Решение.

1. Вычерчиваем балку в масштабе, наносим все нагрузки и размеры и определяем опорные реакции R_A и R_C , используя уравнение статического равновесия:

; ;

; ;

Проверка: ;

;

5 - 1,5·4 - 2 + 3 = 0

Наносим вычисленные значения реакций R_A и R_C на расчетную схему.

2. Запишем для каждого участка I, II, III балки уравнения для Q_y и M_x и, выбрав масштаб, построим их эпюры. Для этого применим метод сечений. На каждом участке проводим произвольные сечения и выбираем начало координат: для участка I – в точке А, для участка II – в точке В, для участка III – в точке D. Произвольные сечения каждого участка связываем с выбранным началом отсчета координат Z₁, Z₂ и Z₃. Тогда для каждого участка получим:

Участок I ().

;

.

При составлении уравнения для M_x считаем, что равнодействующая (qZ₁) от равномерно распределенной нагрузки q приложена посередине рассматриваемого участка длиной Z₁, и тогда плечо ее равно Z₁/2.

При Z₁ = 0; Q_y = 5 т, M_x = 0.

При Z₁ = 1 м; Q_y = 5 – 1,5·1= 3,5 т, M_x= 5·1 – 5·1²/2 = 4,25 тм.

Участок II ().

;

.

При составлении уравнений для Q_y и M_x для участка II видим, что q, приложенная на участке a₁, не зависит от Z₂ (отсчет начинается от точки В).

При Z₂ = 0; Q_y = 5 – 1,5·1 – 2 = 1,5 т, M_x = 5·1 – 1,5·1/2 = 4,25 тм.

При Z₂ = 3 м; Q_y = 5 – 1·2 – 1,5·3 = –3 тм.

M_x = 5·(1+ 3) – 1,5·1(1/2+ 3) – 2·3 – 1,5×3²/2 = 2 тм.

Построив эпюру Q_y для этого участка, видим, что она меняет знак с (+) на (-). Исследуем на экстремум:

; ;

При = 1 м, M_x = 5·(1 + 1) – 1,5·1(1/2 + 1) – 2·1– 1,5×1²/2 = 5 тм.

Откладываем от точки В = 1 м, где Q_y = 0, на эпюре изгибающих моментов откладываем M_x = 5 тм и через полученные три точки проводим параболу – эпюру M_x .

Участок III ( = 2 м).

Q_y = 0; M_x = М = 2 тм.

Выбираем масштаб, строим эпюры (см. рис.) и проверяем их правильность.

2. Определяем опасное сечение балки – сечение, в котором изгибающий момент принимает максимальное значение по абсолютной величине, если, как в нашем случае, материл балки пластичный.

Опасное сечение K, где = 5 тм.

Для подбора сечения балки из условия прочности по нормальным напряжениям при изгибе:

(1)

получим формулу проектировочного расчета:

По сортаменту двутавровых балок (ГОСТ 8239-89) подбираем ближайший больший профиль – двутавр № 24а с осевым моментом сопротивления = 317 см³.

Максимальные рабочие напряжения будут равны, согласно формулы (1),

Недонапряжение составит:

Допустимые пределы отклонения .

Пример 5.

Для заданной расчетной схемы консольной балки (см. рис.) построить эпюры поперечных сил и изгибающих моментов и подобрать деревянную балку круглого поперечного сечения, если Р = 10 кн = 1 т, М = 20 кнм = 2 тм, q = 10 кн/м = 1 т/м, = 1,5 м, = 2 м, l = 3 м, = 8 МПа = 80 кг/см².

Решение.

1. Вычерчиваем расчетную схему балки в масштабе, наносим все нагрузки и размеры. Для консольной балки можно не определять опорные реакции R_A и M_A, но для исключения ошибок при построении эпюр и облегчения контроля их правильности мы будем рекомендовать определять их, используя уравнения статического равновесия:

; ;

; ;

Проверка: ;

;

1 - 1·2 +1 = 0.

Наносим вычисленные значения R_A и на чертеж.

2. Разбиваем балку на участки I, II, III, на каждом участке проводим произвольные сечения и, выбрав для каждого участка начало координат, наносим на чертеж расстояния Z₁, Z₂ и Z₃.

Составляем для каждого участка уравнения для Q_y и M_x и строим эпюры.

Участок I: .

;

.

При Z₁ = 0; Q_y = 1 т, M_x = –1 тм.

При Z₁ = 1,5 м; Q_y = 1 – 1·1,5 = 0,5 т, M_x = –1 + 1·1,5 – 1·1,5²/2= –0,625 тм.

Построив эпюру Q_y, видим, что она меняет знак (+) на (-). Следовательно, на этом участке M_x принимает экстемальное значение – максимум. Исследуем на экстремум:

;

;

При = 1 м; = –1 + 1·1 – 1·1²/2= 0,5 тм.

По полученным трем точкам строим параболу – эпюру M_x.

Участок II: .

;

.

При Z₂ = 0; Q_y = –1 т, ; = 1(0 + (3 – 2)) = 1 тм.

При Z₂ = 0,5 м; = –1 + 1·0,5 = –0,5 т, M_x = 1(0,5 + (3 – 2)) – 1·0,5²/2= 1,375 тм.

Участок III:

= 1 т;

.

При Z₃ = 0; M_x = 0.

При Z₃ = 1 м; M_x = 1×1 = 1 тм.

3. Определяем опасное сечение и подбираем диаметр балки. Опасное сечение в точке В справа, где = 1,375 тм.

Тогда из условия прочности, учитывая, что осевой момент сопротивления для круглого сечения , получим для подбора диаметра d балки формулу:

Округляем диаметр в большую сторону до целого числа, т.е. d =26 см =26·10^-2 м. Тогда максимальные рабочие напряжения будут равны

где = 0,1·26³= 1758 см³.

Недонапряжение составит

Расчет окончен.

Пример 6.

Для консольной балки, нагруженной распределенной нагрузкой интенсивностью кН/м и сосредоточенным моментом кНм (см. рис.), требуется: построить эпюры перерезывающих сил и изгибающих моментов , подобрать балку круглого поперечного сечения при допускаемом нормальном напряжении кН/см² и проверить прочность балки по касательным напряжениям при допускаемом касательном напряжении кН/см². Размеры балки м; м; м.

Решение.

1. Определяем опорные реакции.

Горизонтальная реакция в заделке равна нулю, поскольку внешние нагрузки в направлении оси z на балку не действуют.

Выбираем направления остальных реактивных усилий, возникающих в заделке: вертикальную реакцию направим, например, вниз, а момент – по ходу часовой стрелки. Их значения определяем из уравнений статики:

.

Составляя эти уравнения, считаем момент положительным при вращении против хода часовой стрелки, а проекцию силы положительной, если ее направление совпадает с положительным направлением оси y.

Из первого уравнения находим момент в заделке :

Из второго уравнения – вертикальную реакцию :

кН.

Полученные нами положительные значения для момента и вертикальной реакции в заделке свидетельствуют о том, что мы угадали их направления.

2. Строим эпюры перерезывающих сил и изгибающих моментов .

В соответствии с характером закрепления и нагружения балки, разбиваем ее длину на два участка. По границам каждого из этих участков наметим четыре поперечных сечения (см. рисунок 1), в которых мы и будем методом сечений (РОЗУ) вычислять значения перерезывающих сил и изгибающих моментов.

Сечение 1. Отбросим мысленно правую часть балки. Заменим ее действие на оставшуюся левую часть перерезывающей силой и изгибающим моментом . Для удобства вычисления их значений закроем отброшенную нами правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением.

Напомним, что перерезывающая сила, возникающая в любом поперечном сечении, должна уравновесить все внешние силы (активные и реактивные), которые действуют на рассматриваемую (то есть видимую) нами часть балки. Поэтому перерезывающая сила должна быть равна алгебраической сумме всех сил, которые мы видим.

Приведем и правило знаков для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения со знаком «плюс».

В нашем случае мы видим только реакцию опоры , которая вращает видимую нами часть балки относительно первого сечения (относительно края листка бумаги) против хода часовой стрелки. Поэтому

кН.

Изгибающий момент в любом сечении должен уравновесить момент, создаваемый видимыми нами внешними усилиями, относительно рассматриваемого сечения. Следовательно, он равен алгебраической сумме моментов всех усилий, которые действуют на рассматриваемую нами часть балки, относительно рассматриваемого сечения (иными словами, относительно края листка бумаги). При этом внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. И момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения со знаком «плюс».

Мы видим два усилия: реакцию и момент в заделке . Однако у силы плечо относительно сечения 1 равно нулю. Поэтому

кНм.

Знак «плюс» нами взят потому, что реактивный момент изгибает видимую нами часть балки выпуклостью вниз.

Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).

Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь, в отличие от первого сечения, у силы появилось плечо: м. Поэтому

кН; кНм.

Сечение 3. Закрывая правую часть балки, найдем

кН;

кНм.

Сечение 4. Закроем листком левую часть балки. Тогда

кН;

кНм.

Сечение 5. По-прежнему закроем левую часть балки. Будем иметь

кН;

Сечение 6. Опять закроем левую часть балки. Получим

.

По найденным значениям строим эпюры перерезывающих сил (рисунок 1, б) и изгибающих моментов (рисунок 1, в).

Под незагруженными участками эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклонной прямой вверх. Под опорной реакцией на эпюре имеется скачок вниз на величину этой реакции, то есть на 40 кН.

На эпюре изгибающих моментов мы видим излом под опорной реакцией . Угол излома направлен навстречу реакции опоры. Под распределенной нагрузкой q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре – экстремум, поскольку эпюра перерезывающей силы в этом месте проходит здесь через нулевое значение.

3. Определяем требуемый диаметр поперечного сечения балки.

Условие прочности по нормальным напряжениям имеет вид:

,

где – момент сопротивления балки при изгибе. Для балки круглого поперечного сечения он равен:

.

Наибольший по абсолютному значению изгибающий момент возникает в третьем сечении балки: кНсм.

Тогда требуемый диаметр балки определяется по формуле

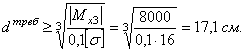
Принимаем мм. Тогда

«Перенапряжение» составляет

,

что допускается.

4. Проверяем прочность балки по наибольшим касательным напряжениям.

Наибольшие касательные напряжения, возникающие в поперечном сечении балки круглого сечения, вычисляются по формуле

,

где – площадь поперечного сечения.

Согласно эпюре Q_y, наибольшее по алгебраической величине значение перерезывающей силы равно кН. Тогда

то есть условие прочности и по касательным напряжениям выполняется, причем, с большим запасом.

Пример 7.

Для шарнирно опертой балки, нагруженной распределенной нагрузкой интенсивностью кН/м, сосредоточенной силой кН и сосредоточенным моментом кНм (см. рис.), требуется построить эпюры перерезывающих сил Q_y и изгибающих моментов и подобрать балку двутаврового поперечного сечения при допускаемом нормальном напряжении кН/см² и допускаемом касательном напряжении кН/см². Пролет балки м.

Решение.

1. Определяем опорные реакции.

Для заданной шарнирно опертой балки необходимо найти три опорные реакции: , и . Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее оси, горизонтальная реакция неподвижной шарнирной опоры A равна нулю: .

Направления вертикальных реакций и выбираем произвольно. Направим, например, обе вертикальные реакции вверх. Для вычисления их значений составим два уравнения статики:

; .

Напомним, что равнодействующая погонной нагрузки q, равномерно распределенной на участке длиной l, равна ql, то есть равна площади эпюры этой нагрузки и приложена она в центре тяжести этой эпюры, то есть посредине длины.

Тогда

;

Делаем проверку: .

Напомним, что силы, направление которых совпадает с положительным направлением оси y, проектируются (проецируются) на эту ось со знаком плюс:

0=0,

то есть верно.

2. Строим эпюры перерезывающих сил и изгибающих моментов .

Разбиваем длину балки на отдельные участки. Границами этих участков являются точки приложения сосредоточенных усилий (активных и/или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких участков в нашей задаче получается три. По границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих моментов (рис. а).

Сечение 1. Отбросим мысленно правую часть балки. Для удобства вычисления перерезывающей силы и изгибающего момента , возникающих в этом сечении, закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка бумаги с самим сечением.

Перерезывающая сила в сечении балки равна алгебраической сумме всех внешних сил (активных и реактивных), которые мы видим. В данном случае мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому

кН.

Знак «плюс» взят потому, что сила вращает видимую нами часть балки относительно первого сечения (края листка бумаги) по ходу часовой стрелки.

Изгибающий момент в сечении балки равен алгебраической сумме моментов всех усилий, которые мы видим, относительно рассматриваемого сечения (то есть относительно края листка бумаги). Мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Однако у силы плечо равно нулю. Равнодействующая погонной нагрузки также равна нулю. Поэтому:

.

Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь мы видим реакцию и нагрузку q, действующую на участке длиной . Равнодействующая погонной нагрузки равна . Она приложена посредине участка длиной . Поэтому

Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).

Сечение 3. Закроем правую часть. Получим

кН;

кНм.

Сечение 4. Закрываем листком правую часть балки. Тогда

кН;

кНм.

Теперь, для контроля правильности вычислений, закроем листком бумаги левую часть балки. Мы видим сосредоточенную силу P, реакцию правой опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому

кН;

кНм.

То есть все верно.

Сечение 5. По-прежнему закроем левую часть балки. Будем иметь

кН;

кНм.

Сечение 6. Опять закроем левую часть балки. Получим

кН;

.

По найденным значениям строим эпюры перерезывающих сил Q_y (рис. б) и изгибающих моментов (рис. в).

Убеждаемся в том, что под незагруженным участком эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по прямой, имеющей наклон вниз. На эпюре Q_y имеется три скачка: под реакцией – вверх на 37,5 кН, под реакцией – вверх на 132,5 кН и под силой P – вниз на 50 кН.

На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой интенсивностью q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. Под сосредоточенным моментом – скачок на 60 кНм, то есть на величину самого момента. В сечении 7 на эпюре – экстремум, поскольку эпюра перерезывающей силы для этого сечения проходит через нулевое значение (). Определим расстояние от сечения 7 до левой опоры.

Перерезывающая сила

.

Отсюда

м.

Экстремальное значение изгибающего момента в сечении 7 равно:

3. Определяем требуемый момент сопротивления балки из условия прочности по нормальным напряжениям.

Согласно эпюре , максимальный по алгебраической величине изгибающий момент возникает в третьем поперечном сечении балки: кНсм. Тогда

По сортаменту подбираем двутавр № 30а, имеющий см³.

4. Проверяем прочность балки по наибольшим касательным напряжениям.

Наибольшие касательные напряжения, возникающие в поперечном сечении двутавровой балки, вычисляются по формуле

.

По сортаменту для выбранного нами двутавра определяем, что статический момент половины сечения относительно нейтральной оси см³, момент инерции относительно нейтральной оси см⁴, а толщина стенки см.

Согласно эпюре Q_y, наибольшее по алгебраической величине значение перерезывающей силы кН. Тогда

то есть условие прочности по касательным напряжениям выполняется.

Пример 8.

Для стальной двухопорной балки (см. рис. 1, а), нагруженную внешними силами F = 4 кН; М = 3 кНм; q = 8 кН/м; с длиной участков l =2 м.

Требуется:

1. Определить опорные реакции.

2. Построить аналитически эпюры поперечных сил и изгибающих моментов.

3. Установить опасные сечения для нормальных и для касательных напряжений.

4. Подобрать двутавровое сечение, приняв = 160 МПа и выполнить его проверку по нормальным напряжениям.

5. Выполнить проверку по касательным напряжениям, приняв = 96 МПа.

6. Построить для соответствующих опасных сечений эпюры нормальных и касательных напряжений.

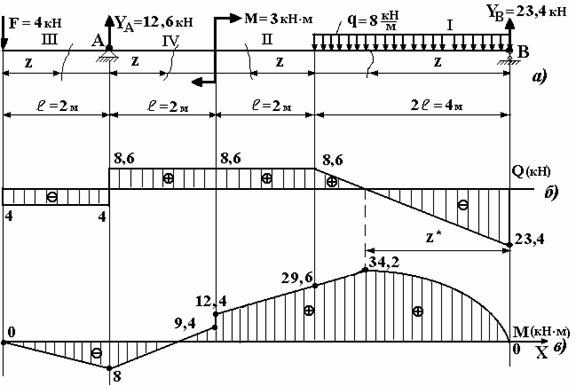
Рис.1

Решение.

1. Из условия статического равновесия определим опорные реакции Y_А и Y_В, произвольно направив их вверх:

; ;

; ;

Проверка: ;

-F + Y_А – q ×2l +Y_В = 0;

- 4 + 12,6 – 8×2×2 + 23,4 =0;

36 –36 = 0.

Таким образом, величина и направление опорных реакций определены верно.

2. Определяем аналитически величины поперечных сил и изгибающих моментов на участках балки и строим эпюры Q (рис. 1, б) и М (рис.1, в)

Для построения эпюры Q проводим параллельно оси балки, ось эпюры и откладываем в масштабе величины поперечных сил с учетом знака.

Затем определяем аналитически значения изгибающих моментов по участкам балки, согласно правилу знаков для изгибающих моментов, и строим в масштабе эпюру М.

Участок I:

z = 0; Q_y = - Y_B = - 23,4 кН; М_Х = 0;

z = 4м; Q_y = - 23,4 + 8 × 4 = 8,6 кН; М_Х = 23,4 × 4 – 8 ×4²/2= 29,6 кНм.

Участок II:

z = 0; ;

z = 2 м; 23,4 (2 × 2 + 2) - 8 × 2 × 2 (2 + 2) = 12,4 кНм.

Участок III:

Q_y = - F = - 4 кН;

M_x = -F z ;

z = 0; ;

z = 2 м;

Участок IV:

Q_y = - F + Y_A = - 4 + 12,6 = 8,6 кН;

;

z = 0; ;

z = 2 м;

На первом участке видим, что эпюра поперечных сил пересекла ось на каком-то расстоянии z^*. Это говорит о том, что в этой точке на эпюре изгибающего момента возникает экстремум.

Для определения экстремального значения изгибающего момента первого участка найдем расстояние z^* из уравнения поперечной силы первого участка, зная, что эта величина в данной точке равна нулю:

z^* =.

Подставляем в уравнение изгибающего момента первого участка найденное значение z^* и вычисляем экстремальный изгибающий момент:

После этого строим эпюру изгибающих моментов по участкам балки (рис. 1,в), откладывая величину изгибающего момента в начале и конце каждого участков c учетом знака. Затем, обращая внимание на степенной показатель переменной величины z – длины участка в общем уравнении изгибающего момента, соединяем соответствующей линией эти точки.

Первый участок имеет уравнение изгибающего момента с переменной величиной z во второй степени, т.е. начальную, экстремальную и конечную точки величин изгибающих моментов первого участка соединяем параболической кривой. На остальных трех участках переменная функция z в первой степени, что показывает линейную зависимость изменения величины изгибающих моментов.

3. Устанавливаем опасные сечения по нормальным и касательным напряжениям.

Опасное сечение по нормальным напряжениям определяется по максимальному изгибающему моменту М.

В нашей задаче это будет точка экстремума на первом участке (рис. 1,в) балки при М_max = 34,2 кНм.

Опасное сечение по касательному напряжению будет в точке опоры В, где максимальная величина поперечной силы (рис.1,б). Q_max = 23,4 кН.

4. Из условия прочности по нормальным напряжениям подбираем двутавровое сечение:

; .

Из сортамента принимаем ближайшую большую величину W_x = 232 см³ и выписываем необходимые значения для двутаврового прокатного профиля № 22: h = 22 см; В = 11 см; d = 0,54 см; t = 0,87 см; J_x = 2550 см⁴; S_x = 131 см³.

5. Строим эпюру нормальных напряжений (рис.2,б).

Для этого вычисляем напряжения в крайних точках 1 и 1’ поперечного сечения при (рис.2,а).

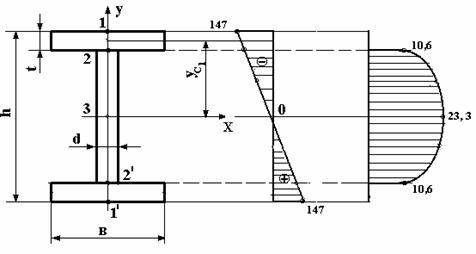
Эп., МПа Эп., МПа

а) б) в)

Рис. 2

где J_x - момент инерции площади поперечного сечения двутавра относительно оси х; y - расстояние от нейтральной оси до точек 1 и 1’.

Недогрузка по нормальным напряжениям составляет

6. Построение эпюры касательных напряжений (рисунок 2,в). С этой целью вычисляем напряжения в точках 2, 2’ и 3 по формуле Журавского:

.

Опасным сечением по касательным напряжениям является сечение, в котором возникает наибольшее по абсолютной величине внутренняя поперечная сила. В нашем случае опасным сечением является – сечение В, в котором Q_max = 23,4 кН.

Максимальные касательные напряжения возникают в нейтральном слое поперечного сечения, т.е. в точке 3 (рис. 2). Тогда

,

где S_x = 131 см³ – максимальный статический момент половины площади поперечного сечения, взятый из сортамента.

Условие прочности выполняется, т.к.

Вычислим напряжения в точках 2 и 2’. Для этого определим статический момент отсеченной площади, расположенной выше точки 2:

По формуле Журавского вычисляем касательные напряжения в точках 2 и 2’:

По полученным значениям величин касательных напряжений в выбранном масштабе строим эпюру (рисунок 2,в).

Пример 9.

Построить эпюры перерезывающих сил и изгибающих моментов и подобрать размеры круглого поперечного сечения балки (см. рис. а), если , P=30 Кн, a=1 м.

а) б)

Решение.

1. Определение опорных реакций из уравнений равновесия

Составим два независимых уравнения равновесия:

Находим опорные реакции

2. Определение перерезывающей силы Q_y и изгибающего момента M_x методом сечений и построение графиков-эпюр.

Из уравнений равновесия отсеченных частей балки на первом и втором участках находим

На первом участке – постоянная величина, а график изменения момента – прямая линия. Полагая, что , находим . При получаем . Откладываем эти величины на рис. а и соединяем прямой линией.

На втором участке – постоянная величина, а момент изменяется по закону прямой. Полагая, что , получаем . Принимая , находим . Откладываем на графике эти значения и соединяем полученные точки прямой линией.

У строителей эпюру изгибающих моментов принято строить на растянутых волокнах балки (рис. в). Пунктиром показана изогнутая ось балки. Как видно, эпюра M_x в этом случае получится из предыдущей путем ее переворачивания.

3. Контроль правильности построения эпюр с помощью правила Журавского

Из дифференциальных зависимостей Д. Журавского

следует, что на обоих незагруженных участках, где , эпюра перерезывающих сил постоянна , а эпюра изгибающих моментов – наклонная прямая линия. Так как на первом участке , то эпюра M_x с ростом z₁ возрастает. На втором участке , эпюра M_x с ростом должна убывать. Построенные эпюры полностью соответствуют правилам Д. Журавского. В сечении, где действует сосредоточенная сила , на эпюре Q_y имеет место скачок на соответствующую величину этой силы в ее направлении, а на эпюре M_x − излом, резкое изменение угла наклона.

4. Расчет на прочность

Из эпюры находим, что в опасном сечении . Условие прочности имеет вид

Различают три типа расчета:

1) проверочный, когда все величины в условии прочности известны;

2) определение допускаемой величины нагрузки ;

3) проектировочный, для определения размеров поперечного сечения. В этом случае условие прочности следует записать в виде

и вычислить W_x. Если поперечное сечение круглое диаметром D, то момент сопротивления поперечного сечения . Из условия прочности находим

мм.

Полученное численное значение диаметра округляют и делают проверочный расчет. Примем D=10 мм.

Пример 10.

Построить эпюры для консольной балки (см. рис.а) и подобрать размеры прямоугольного поперечного сечения, если , q=40 Кн/м, l=1,5 м

а) б)

Решение.

1. Определение опорных реакций

Из уравнений равновесия

находим

2. Определение методом сечения и построение эпюр

Из уравнений равновесия отсеченной части балки (рисунок 1, б) находим

.

Эпюры представлены на рис. а. Выпуклость параболы эпюры M_x определяется знаком второй производной либо правилом зонтика и дождика (на сжатом волокне).

Расчет на прочность

Из эпюры M_x в опасном сечении (заделке) находим . Условие прочности записываем в виде

.

Пусть требуется подобрать размеры прямоугольного поперечного сечения с соотношением сторон . Тогда . Из условия прочности находим

мм.

Примем b=7 мм, тогда h=2b=14 мм.

Пример 11.

Построить эпюры для консольной балки (см. рис. а) и подобрать двутавровое поперечное сечение.

а) б)

Решение.

1. Определение опорных реакций

Из уравнений равновесия

находим

2. Определение методом сечения и построение эпюр

Мысленно рассечем балку и рассмотрим правую ее часть (рис. б). Из уравнения равновесия находим

Эпюры представлены на рис. a.

Консольная балка не загружена распределенной нагрузкой, поэтому перерезывающая сила по правилу Журавского постоянна, а момент – прямая, возрастающая с ростом , поскольку .

3. Расчет на прочность

Из эпюры в опасном сечении находим . Условие прочности записываем в виде

.

Пусть требуется подобрать поперечное сечение в виде стандартного двутавра. Тогда условие прочности представим в виде

.

Пусть . Тогда .

Из таблицы сортамента по ГОСТ 8239-89 берем первое большее значение, что соответствует двутавру № 22 с . Расчетное напряжение

МПа,

что меньше допустимого на 19,2%, это слишком большое недонапряжение, приводящее к дополнительной затрате материала.

Возьмем двутавр № 20 по ГОСТ 8239-89 с . Расчетное напряжение составит

МПа.

Перенапряжение составляет 1%, что меньше допустимого в инженерных расчетах.

Окончательно выбираем двутавровое сечение балки № 20.

Пример 12.

Построить эпюры для балки с внутренним шарниром (см. рис. а) и определить допускаемое значение q, если и поперечное сечение балки двутавр № 20.

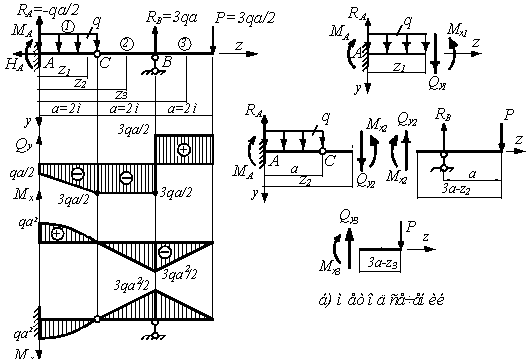
а) б)

Решение.

1. Определение опорных реакций из уравнений равновесия

Балка имеет четыре простые связи и один внутренний шарнир, который снимает одну простую связь. Следовательно, балка статически определимая. Мы можем составить четыре уравнения равновесия, одно из которых может служить для проверки правильности определения опорных реакций:

Из второго, третьего и четвертого уравнений находим

.

Подставляя найденные значения реактивных сил в первое уравнение, убеждаемся, что оно тождественно уравнивается:

.

Следовательно, реакции определены правильно.

2. Определение методом сечения и построение их эпюр

Балка имеет три участка с различными аналитическими выражениями для внутренних силовых факторов. Методом сечений из уравнений равновесия отсеченных частей (рис. б) находим

при

при

при

На первом участке эпюра − прямая линия, убывающая с ростом , а эпюра − квадратичная парабола.

При . При имеем момент во внутреннем шарнире . Эпюра моментов экстремума не имеет, так как на первом участке перерезывающая сила в нуль нигде не обращается. Эпюра имеет по правилу зонтика выпуклость вверх и с ростом убывает.

На втором участке эпюра постоянна, а эпюра − прямая линия, убывающая с ростом , так как угловой коэффициент отрицателен. При имеем , а при .

На третьем участке эпюра постоянна, а − прямая линия, возрастающая с ростом , так как угловой коэффициент . При , а при . На эпюре в сечении имеет место скачок на величину силы в направлении действия этой силы.

Построенные эпюры внутренних усилий полностью соответствуют правилам построения эпюр, которые следуют из дифференциальных зависимостей Д. Журавского.

3. Расчет на прочность

Из эпюры изгибающих моментов для опасного сечения находим .

Условие прочности

или после подстановки значения

Для определения допускаемого значения q из условия прочности получаем

Из таблиц сортамента ГОСТ 8239-89 для двутавра № 20 находим м³.

Тогда

Пример 13.

На балку круглого поперечного сечения действует нагрузка, показанная на рис. 1,а. Требуется подобрать размеры поперечного сечения (или определить грузоподъемность балки) так, чтобы выполнялись условия прочности во всех опасных точках.

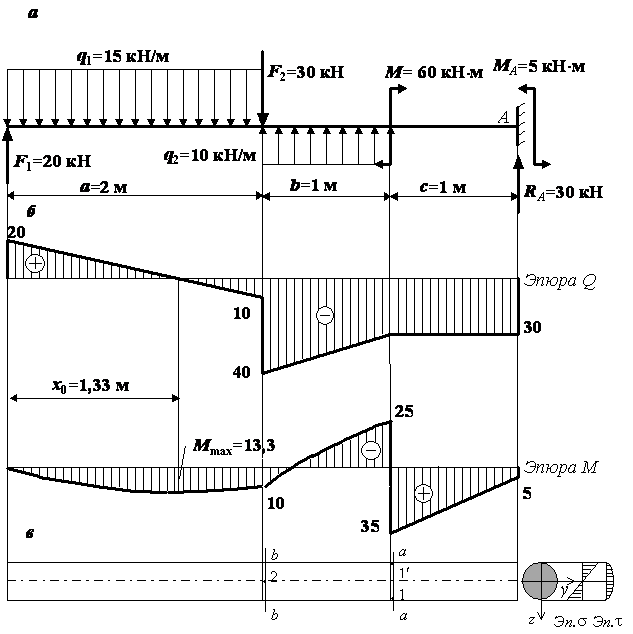
Рис.1

Решение.

Строим эпюры Q и М (рис. 1, б). Эпюры Q и М нужны для того, чтобы найти положение опасных сечений и опасных точек в балке. Найдем положение опасных сечений для этой балки. Опасными сечениями в балках круглого и прямоугольного сечений являются:

- сечение, где действует максимальный по модулю изгибающий момент (сечение а–а на рис. 1, в);

- сечение, где действует наибольшая по абсолютной величине поперечная сила (сечение b–b на рис.1, в).

В опасных сечениях находятся опасные точки – точки, в которых действуют либо максимальные нормальные, либо максимальные касательные напряжения. Чтобы найти положение опасных точек, посмотрим на эпюры распределения нормальных s и касательных напряжений по высоте балки, которые построены на рис. 1, в. Из эпюры s видно, что наибольшие нормальные напряжения действуют в точках, наиболее удаленных от нейтральной оси y. Таким образом, опасными точками с максимальными нормальными напряжениями являются точки 1, 1¢, расположенные в сечении а–а (рис. 1, в). В одной точке действуют максимальные растягивающие напряжения, в другой – максимальные сжимающие. В данной задаче в сечении а–а максимальный момент положителен, т.е. он изгибает балку выпуклостью вниз, поэтому в точке 1 действуют растягивающие, а в точке 1¢ – сжимающие напряжения. Если допускаемые напряжения при растяжении и сжатии материала балки одинаковы (дерево или пластичный материал), то обе точки являются равноопасными. Опасная точка с максимальными касательными напряжениями, как видно из эпюры t, расположена на оси балки в сечении b–b, где действует наибольшая поперечная сила (точка 2 на рис.1, в).

Запишем условия прочности в опасных точках. Начнем с рассмотрения опасных точек 1, 1¢, так как именно эти точки чаще всего бывают наиболее опасными. Эти точки находятся в линейном напряженном состоянии (рис. 2, а) и условие прочности в этих точках записывается так же, как при растяжении-сжатии:

,

где максимальные напряжения определяем по формуле .

Рис.2

Тогда условие прочности в точках 1, 1¢ будет иметь вид

.

Если стоит задача подбора сечения, то из этого условия находим требуемый момент сопротивления балки:

,

а, зная момент сопротивления, по формулам ; . определяем размеры поперечного сечения балки. Например, для балки круглого поперечного сечения необходимый радиус . Для деревянных балок диаметр ходовых бревен ограничен и не должен быть больше 26 см. Для бревна с радиусом 13 см момент сопротивления равен 1725 см³ . Если полученное из условия прочности значение необходимого момента сопротивления будет больше 1725 см³, то следует подобрать сечение из нескольких бревен. В рассматриваемом примере для деревянной балки с = 10 МПа = 1кН/см² найдем см³. Тогда количество бревен . И радиус одного из трех бревен будет см.

Если требуется определить грузоподъемность балки, то из условия прочности в точках 1, 1¢ находим максимальное значение изгибающего момента:

,

которое зависит от нагрузки. Зная эту зависимость из эпюры М, найдем значение допускаемой нагрузки.

Решение задачи будет закончено только тогда, когда мы убедимся, что полученный размер поперечного сечения балки (или найденная допускаемая нагрузка) удовлетворяют условию прочности во второй опасной точке. Поскольку в точке 2 действуют только касательные напряжения (нормальные напряжения в точках, лежащих на оси балки, равны нулю – это видно из эпюры на рис.1, в), то напряженное состояние этой точки – чистый сдвиг (рис. 2, б). Если неизвестно опытное значение допускаемого касательного напряжения, то условие прочности при чистом сдвиге записывается по соответствующей материалу балки теории прочности. Например, для пластичного материала из формул , для чистого сдвига можно записать такие условия прочности для точки 2:

– по третьей теории и

– по четвертой теории прочности.

Для деревянной балки, а дерево – анизотропный материал, теории прочности, полученные для изотропных материалов, не справедливы. В этом случае для проверки прочности необходимо знать допускаемое значение касательного напряжения , полученное на основании опытных данных. Тогда для деревянной балки условие прочности в точке 2 записывается так:

.

Здесь максимальное касательное напряжение определяем в зависимости от формы поперечного сечения по формулам ; . Например, для рассматриваемой балки с подобранным сечением из трех бревен радиусом 12 см

кН/см²,

что меньше = 2 МПа = 0,2 кН/см².

Если условие прочности в точке 2 выполняться не будет, то необходимо подобрать сечение или найти грузоподъемность балки из условия прочности в этой точке.

Пример 14.

Стальная прокатная двутавровая балка загружена нагрузками, показанными на рис. 1, а. Подберем номер двутавра так, чтобы выполнялись условия прочности во всех опасных точках.

Рис.1

Решение.

Строим эпюры Q и М. По построенным эпюрам Q и М (рис.1, б) найдем положение опасных точек в двутавровой балке. Сначала покажем на фасаде балки опасные сечения. Кроме опасных сечений, где действуют максимальный изгибающий момент (сечение а–а на рис.1, в) и наибольшая поперечная сила (сечение b–b на рис.1, в), в двутавровой балке существует еще одно опасное сечение – это сечение, где Q и М одновременно имеют большие значения. В рассматриваемом примере это сечение с–с на рис.1, в. В опасных сечениях находятся опасные точки. В сечении а–а – точки 1, 1¢ с максимальными нормальными напряжениями, в сечении b–b – точка 2, в которой действует наибольшее касательное напряжение. Особенностью проверки прочности двутавровой балки является появление новых по сравнению с балками круглого и прямоугольного сечений опасных точек. Это связано с особенностью эпюры распределения касательных напряжений по высоте двутавра. Точки 3, 3¢, находящиеся в сечении с–с и расположенные в крайних точках стенки на сопряжении с полкой (рис.1, в), опасны, так как в них одновременно действуют большие нормальные и большие касательные напряжения.

Подберем размер двутавра (номер двутавра) из условия прочности в точках 1, 1¢ – именно эти точки являются, как правило, наиболее опасными, а затем проверим прочность в остальных опасных точках. Точки 1, 1¢ находятся в линейном напряженном состоянии и условие прочности в этих точках имеет вид

.

Отсюда определяем необходимый момент сопротивления . По таблице сортамента прокатной стали подбираем номер двутавра, у которого момент сопротивления имеет близкое к значение. (Обратите внимание, что в таблице сортамента – другое обозначение осей и принятому нами обозначению там соответствует ). Для балки, изображенной на рисунке, выполненной из стали С-235 с допускаемым напряжением 160 МПа,

см3,

и в соответствии с ГОСТ 9239–89 подбираем двутавр № 33, у которого см³.

После того, как найден номер двутавра, необходимо убедиться, что выполняются условия прочности в остальных опасных точках. Точка 2, в которой нормальные напряжения равны нулю, а касательные – максимальны, находится в напряженном состоянии "чистый сдвиг" и условие прочности в ней записывается по теории прочности, справедливой для пластичных материалов или . Максимальные касательные напряжения находим по формуле Журавского . Рассмотрим подробно как находить статический момент отсеченной части , входящий в формулу Журавского. Статический момент отсеченной части зависит от того, где находится точка, в которой определяется касательное напряжение. Чтобы найти отсеченную часть, надо мысленно разрезать поперечное сечение через точку, в которой ищем , перпендикулярно направлению касательного напряжения. Любая из "отрезанных" частей может считаться отсеченной.

Рис.2

Для точки 2 отсеченная часть сечения показана на рис. 2, а (заштрихованная часть) – это половина сечения. Для простых фигур (прямоугольник, круг), положение центра тяжести которых известно, статический момент находится по формуле

,

где А – площадь фигуры; – координата центра тяжести (при вычислении статического момента отсеченной части знак координаты не учитывается, в этом случае – это расстояние от центра тяжести отсеченной части до оси y). Для вычисления статического момента отсеченной части, показанной на рис. 2, а, разобьем ее на два прямоугольника: полку и половину стенки. Для каждого прямоугольника находим площадь и расстояние от центра тяжести до оси y. Тогда

.

В этой формуле первое слагаемое – статический момент полки, а второе – статический момент половины стенки. Заметим, что для стандартных двутавров статический момент половины сечения задан в сортаменте (обозначен ) и для найденного двутавра № 33 см³. В формуле Журавского для точки 2 – толщина стенки двутавра, – осевой момент инерции находим по таблице сортамента прокатных двутавров (обозначен). Подставляя данные для двутавра № 33, получим

кН/см².

Сравнивая максимальное касательное напряжение согласно третьей теории прочности с кН/см² , убеждаемся, что условие прочности в точке 2 выполняется.

Проверим прочность в точках 3, 3¢, которые находятся в "балочном" напряженном состоянии (см. рис. 3).

Рис.3

Найдем напряжения, действующие в точке 3. Нормальное напряжение ищем по формуле . Координата точки 3 и

кН/см².

Положительный знак полученного напряжения показывает, что в точке 3, расположенной выше нейтральной оси, действует растягивающее напряжение. Для определения касательного напряжения по формуле Журавского получим сначала статический момент отсеченной части. Отсеченной частью сечения для точки 3 будет полка (см. рис. 2, б) и

см³.

Так как точка 3 находится в стенке двутавра, то см. Тогда касательное напряжение в точке 3

кН/см².

Подставляя найденные значения и в условие прочности по третьей теории , убеждаемся в том, что оно удовлетворяется:

кН/см².

На этом процесс подбора двутавра заканчивается.

При решении задачи требуется еще исследовать напряженное состояние произвольной точки двутавра. Эта часть задачи не имеет отношения к проверке прочности двутавра, носит академический характер и необходима для лучшего освоения теории изгиба. После того, как Вы выбрали произвольную точку, расположенную в сечении, где и Q, и М не равны нулю, найдите нормальное и касательное напряжения в этой точке по формулам и , используя те навыки, которые Вы приобрели при определении напряжений в опасных точках. Выделите вокруг исследуемой точки элементарный параллелепипед (элемент) и покажите на рисунке действующие на гранях элемента напряжения с учетом их знаков. Дальше определите главные напряжения и положение главных площадок, применяя знания, полученные при изучении раздела "Исследование плоского напряженного состояния". Поверните на рисунке элемент по главным направлениям и покажите на его гранях главные напряжения.

Пример 15.

Построить эпюры поперечной силы Q и изгибающего момента М для балки, показанной на рисунке, а также определить размеры круглого, прямоугольного (h/b = 2) и двутаврового сечения. Проверить прочность двутавра по главным напряжениям, если: F₁ = 3 кН, F₂ = 1,5 кН, М = 5,1 кНм, q =2кН/м, а = 2м, b = 1 м, с = 3м, = 150 МПа, = 100 МПа.

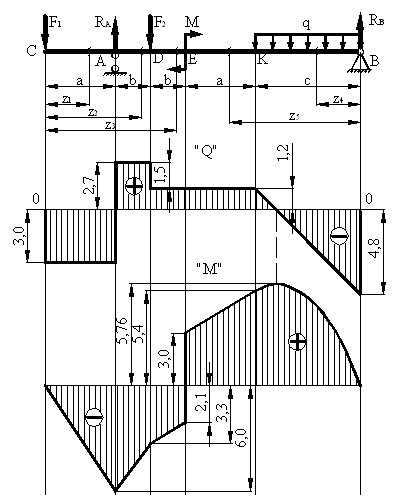
Решение.

1) Определяем опорные реакции.

; ;

; ;

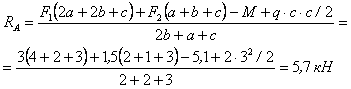
Проверка:

; ;

- реакции найдены верно

2) Разбиваем балку на участки CA, AD, DE, EK, KB.

3) Определяем значения Q и М на каждом участке.

СА

, ; , .

АD

, ;

, .

DE

, ;

, .

КВ

, , ;

, , .

Найдем максимум изгибающего момента на участке KB.

Приравняем уравнение Q на этом участке к нулю и выразим координату z_max, при которой Q = 0, а момент имеет максимальное значение. Далее подставим z_max в уравнение момента на этом участке и найдем M_max.

EК

, ;

, .

4) Строим эпюры

5) Определяем из условия прочности необходимый момент сопротивления

6) Определяем размеры круглого сечения

7) Определяем размеры прямоугольного сечения

8) Подбираем по сортаменту двутавровую балку № 10 (ГОСТ 8239-89)

W_X = 39,7 см³, S_X^* =23 см³, I_X = 198 см⁴, h = 100 мм, b = 55 мм, d = 4,5 мм, t = 7,2 мм.

Для проверки прочности балки по главным напряжениям, необходимо построить эпюры нормальных и касательных напряжений в опасном сечении. Так как величина главных напряжений зависит и от нормальных и от касательных напряжений, то проверку прочности следует произвести в том сечении балки, где М и Q достаточно велики. На опоре В поперечная сила Q имеет максимальное значение, однако здесь М = 0. поэтому считаем опасным сечение на опоре А, где изгибающий момент максимален и поперечная сила имеет сравнительно большое значение.

Нормальные напряжения, изменяясь по высоте сечения, подчиняются линейному закону:

,

где y – координата точки сечения.

при у = 0, = 0;

при ,

Закон изменения касательных напряжений определяются законом изменением статического момента площади, который, в свою очередь изменяется по высоте сечения по параболическому закону. Вычислив значение для характерных точек сечения, построим эпюру касательных напряжений. При вычислении значений t воспользуемся обозначениями размеров сечения, принятыми на рисунке.

;

Как видно из эпюр, опасным в сечении является слой 3–3, где нормальные и касательные напряжения имеют значения близкие к максимальным, в то время как в слое 1–1, где , = 0, а в слое 4–4, где , = 0.

Определяем главные напряжения по третьей теории прочности

- условие прочности для слоя 3–3 выполняется.

Пример 16.

Для заданной балки построить эпюры поперечных сил и изгибающих моментов и подобрать из условия прочности ( = 160 МПа) двутавровое сечение. Выполнить проверку по главным напряжениям. а = 1м; Р = 15 кН; М = 26 кНм; q = 20 кН/м

Решение.

При расчете балок на прочность необходимо отыскать опасное сечение балки, через которое передаются наибольшие напряжения, которые в свою очередь не должны превышать допускаемые напряжения. Для расчета балок из пластичных материалов рекомендуется пользоваться условиями прочности, полученными по III и IV теориям прочности:

(1)

(2)

где – нормальное напряжение, зависящее от изгибающего момента М в сечении, координаты точки y и осевого момента инерции J;

– касательное напряжение, зависящее от поперечной силы Q, осевого момента инерции J, ширины сечения b и статического момента S_z(y) площади поперечного сечения, заключенной между уровнем у и краем сечения.

(3)

(4)

Для нахождения опасного сечения необходимо построить эпюры поперечных сил Q и изгибающих моментов M.

Поскольку балка не консольная, то, прежде всего, определяем реакции опор R_А и R_В. Составляем уравнения моментов относительно точек А и В:

(5)

кН

(6)

кН

Проверим, правильно ли найдены реакции.

(7)

Делим балку на участки по местам приложения сосредоточенных нагрузок и местам начала и конца действия распределенной нагрузки. Для каждого участка записываем уравнения для определения поперечной силы и изгибающего момента при помощи метода сечений.

I участок. Рассекаем в произвольном месте на первом участке балку на расстоянии х₁ от начала участка. Причем

Поперечную силу определяем, находя сумму проекций всех сил на ось, перпендикулярную оси участка. Силы, пытающиеся повернуть рассматриваемое сечение по ходу часовой стрелки, входят в уравнение со знаком «+»

(8)

Получили линейную зависимость поперечной силы от координаты х₁.

определяем значения поперечной силы по краям участка

кН

кН.

Поскольку поперечная сила меняет знак, то внутри участка на эпюре моментов в каком то сечении будет экстремальное значение момента. Определим координату этого сечения х₁₀, приравняв выражение поперечной силы к нулю.

(9)

м

Изгибающий момент в сечении определяем как сумму моментов всех сил относительно точки, в которой взято сечение.

(10)

Вид эпюры моментов на данном участке – парабола с вершиной с координатой х₁₀.

Для построения эпюры моментов достаточно определить значения изгибающих момента для трех точек участка:

кНм

кНм

II участок. Рассекаем в произвольном месте на втором участке балку на расстоянии х₂ от начала участка. Причем

кН (11)

Поперечная сила имеет постоянное значение по всей длине участка.

(12)

Получили линейную зависимость изгибающего момента от координаты х₂. Для построения эпюры изгибающего момента на данном участке достаточно определить значения изгибающих моментов по краям второго участка.

кНм

кНм

III участок. Рассекаем в произвольном месте на третьем участке балку на расстоянии х₃ от правого начала участка. Причем

кН (13)

кНм (14)

Для построения эпюры поперечных сил берем нулевую линию, параллельную оси балки и откладываем в масштабе значения поперечных сил перпендикулярно нулевой линии. На всех участках линейная зависимость поперечной силы, поэтому откладываемые значения на краях участков соединяем прямыми линиями. Поле эпюры штрихуем перпендикулярно нулевой линии и указываем знаки поперечных сил. Слева от эпюры указываем название эпюры «Q» и указываем размерность «кН».

Для построения эпюры изгибающих моментов берем нулевую линию, откладываем значения изгибающих моментов для характерных точек балки и соединяем эти значения в зависимости от выражений изгибающего момента на соответствующих участках.

На первом участке выражение изгибающего момента представляет собой уравнение параболы, причем вершина параболы будет находиться под нулевым значением поперечной силы на эпюре поперечных сил. Выпуклость параболы направлена на встречу равномерно распределенной нагрузке.

На втором участке линейная зависимость изгибающего момента, поэтому значения на краях участка соединяем прямой линией.

На третьем участке изгибающий момент имеет постоянное значение.

Выполняем штриховку перпендикулярно нулевой линии, предварительно указав знаки в поле эпюры.

Слева от эпюры указываем название эпюры «М» и размерность откладываемых величин «кНм».

После построения эпюры определяем опасное сечение.

В точке В максимальный изгибающий момент и максимальная поперечная сила:

М = 26 кНм

Q = 32 кН

По максимальному моменту подбираем сечение из условия прочности при изгибе:

(15)

где W – момент сопротивления поперечного сечения. Для двутавровых сечений приведен в сортаменте прокатной стали в зависимости от номера проката.

Из (15)

(16)

м³

или

см³

По таблице сортамента подбираем двутавровое сечение № 20 и выписываем для этого сечения следующие данные:

Осевой момент инерции относительно оси z J_z = 1840 см⁴;

Статический момент полусечения S_z = 104 см³;

Момент сопротивления W_z = 184 см³;

Высота сечения h = 200 мм;

Ширина полки b = 100 мм;

Толщина стенки d = 5,2 мм;

Средняя толщина полки t = 8,4 мм.

Проведем проверку выбранного поперечного сечения по главным напряжениям

Выберем для проверки пять точек в поперечном сечении:

1 точка - на поверхности двутаврового сечения с координатой у₁ = h/2. Статический момент S_z(y = h/2) = 0;

2 точка - на переходе от полки швеллера к стенке с шириной сечения b₂ = b и с координатой у₂ = h/2 – t;

Статический момент S_z (y=h/2-t) равен статическому моменту полки. С достаточной точностью полку можно считать прямоугольником с размерами b×t. Тогда

3 точка - на переходе от полки швеллера к стенке с шириной сечения b₃ = d и с координатой у₃ = h/2 – t; Статический момент такой же как и для второй точки.

4 точка - в центре сечения с шириной сечения b₄ = d и с координатой у₄ = 0.

Статический момент S_z(y = 0) равен статическому моменту полусечения S_z

Определяем по (3) и (4) для первой точки:

Па (17)

(18)

Для второй точки

Па (19)

Па (20)

Для третьей точки

Па (21)

Па (22)

Для четвертой точки

Па (23)

Па (24)

Строим эпюры нормальных и касательных напряжений.

По эпюре изгибающих моментов видно, что сжаты нижние волокна, поэтому на эпюре нормальных напряжений в верхней части сечения будут положительные (растягивающие) напряжения, а в нижней – отрицательные (сжимающие)

По третьей теории прочности (1):

(25)

(26)

(27)

(28)

Условие (1) выполняется. Сечение подобрано правильно.

Пример 17.

Целью настоящей задачи является овладение навыками построения эпюр внутренних силовых факторов при изгибе балок и их расчет на прочность (подбор необходимого поперечного сечения). При этом необходимо усвоить сущность метода сечений, правило знаков для внутренних силовых факторов, порядок построения эпюр и методику вычерчивания приблизительного вида изогнутой оси изгибаемых элементов, а также суть расчета на прочность при изгибе.

Задачу будем решать в следующей последовательности:

1) Из уравнений равновесия (статики) найдем опорные реакции и проверим правильность их вычисления.

2) Установим количество характерных участков системы, в пределах каждого, из которых закон изменения изгибающего момента и поперечной силы неизменен. При этом границами участков будем считать точки, в которых происходит изменение характера приложения внешней нагрузки (появление сосредоточенных сил или моментов, начало или конец приложения распределенной нагрузки), а также изменение геометрических характеристик сечения балки или направления её оси.

3) Используя метод сечений, составим аналитические выражения для внутренних силовых факторов на каждом из участков в зависимости от текущей координаты вдоль оси балки.

4) Определим числовые значения внутренних силовых факторов в характерных сечениях на каждом из участков. Как правило, такими сечениями являются начало и конец участка, а также точка на оси балки, в которой изгибающий момент принимает экстремальное значение. (Эта точка требуется лишь в случаях, когда эпюра поперечной силы на рассматриваемом участке пересекает ось абсцисс, то есть Q принимает нулевое значение).

5) Строим эпюры внутренних силовых факторов, располагая их под расчетной схемой балки. При этом положительные значения ординат поперечных сил откладываем вверх, а отрицательные – вниз, в то время как эпюры изгибающих моментов строятся на растянутых волокнах. Знаки проставляются только на эпюрах поперечных сил.

6) Производим проверку правильности построения эпюр на основании дифференциальных зависимостей между изгибающим моментом и поперечной силой.

7) Изображаем примерный вид изогнутой оси балки.

8) Определяем опасное сечение, в котором действует наибольший по абсолютной величине изгибающий момент.

9) Из условия прочности при изгибе определяем наименьшее предельное значение момента сопротивления сечения.

10) Принимая во внимание конструктивные особенности и тип сечения, определяем характерные размеры (b и h в случае прямоугольного поперечного сечения или номер двутавра – в случае применения сортового проката).

Схема I. Консольная балка

1. При расчете консольной балки рекомендуется начинать ее обход со свободного конца и двигаться в сторону заделки. В этом случае опорные реакции на данном этапе расчета можно не определять, а их величины впоследствии взять с эпюр внутренних силовых факторов.

2. Поскольку в рассматриваемых нами задачах изгибная жесткость всех участков балки предполагается одинаковой, а ее ось – прямолинейной, то о начале каждого нового участка можно будет судить по изменениям характера внешней нагрузки. Так, двигаясь справа налево (в сторону заделки), мы видим силу P, что говорит о начале второго участка, и, далее, распределенную нагрузку q, которая продолжается до конца балки и заделки, тем самым определяя протяженность третьего, последнего участка (рис.1, а).

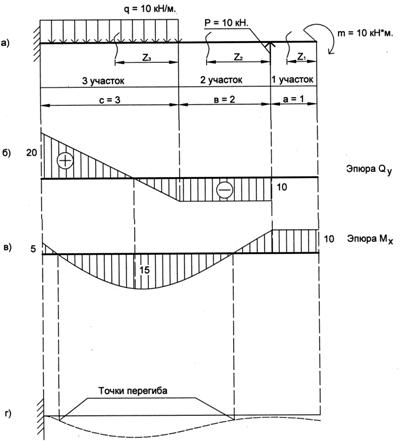
Рис.1

3. На протяжении каждого из указанных участков законы изменения изгибающего момента M_x и поперечной силы Q_y будут неизменными и полученные нами уравнения будут справедливы для любой точки в их пределах. Таким образом, следует трижды рассечь балку (рис.1, а) и в каждом случае выписать выражения для поперечной силы и изгибающего момента (рис. 2).

Проводя последовательно сечения на первом, втором и третьем участках, рассмотрим равновесие правой отсеченной части, приложив к ней все действующие справа от сечения заданные нагрузки, и внутренние силовые факторы в положительном направлении.

Имеем:

Для первого участка ( ):

Q_y = 0 (силы отсутствуют)

Рис.2

M_x = - m

Для второго участка ():

Q_y = - P

M_x = - m + P z₂

Для третьего участка ( ):

Q_y = - P + q z₃

M_x = - m + P( b + z₃ ) - q/2

Определим теперь значения Q_y и M_x в характерных сечениях (рассмотрим пока только точки начала и конца участков).

Первый участок:

Q_y = 0

M_x = - m

Очевидно, что величины Q_y и M_x от координаты z не зависят.

Второй участок:

При z = 0 Q_y = - P M_x = - m

При z = b Q_y = - P M_x = - m + Pb

Здесь Q_y – константа ( не зависит от координаты z в пределах второго участка), а M_x - наклонная прямая ( параметр z входит в уравнение в первой степени ).

Третий участок:

При z = 0 Q_y = - P M_x = - m + P b

При z = c Q_y = - P + q c M_x = - m + P(b + c) - q c ²/2

На этом участке сила Q_y изменяется по линейному закону (её эпюра представляет собой наклонную линию), а момент M_x - по закону квадратной параболы (параметр z входит в уравнение во второй степени ).

Для построения параболической кривой двух точек может оказаться недостаточно. Однако, при решении рассматриваемой задачи нас будут интересовать только максимальные ( по абсолютной величине ) значения момента в пределах каждого из участков, поэтому, если эпюра M_x на рассматриваемом участке не имеет экстремума, то наибольшим будет одно из граничных значений функции M_{x ,} если же такой экстремум существует, то его определением мы займемся ниже.

4. Для наглядности предположим, что входящие в уравнения величины имеют следующие числовые значения:

a = 1 м, b = 2 м, c = 3 м, P = 10 кН, m = 10 кНм, q = 10 кН/м .

Подставляя их в ранее полученные аналитические выражения, будем иметь следующие результаты:

№ участка	z, м	Qy , кН	Mx , кНм
1 участок	z = 0 z = 1	Qy = 0 Qy = 0	Mx = -10 Mx = -10
2 участок	z = 0 z = 2	Qy = -10 Qy = -10	Mx = -10 Mx = +10
3 участок	z = 0 z = 3	Qy = -10 Qy = +20	Mx = +10 Mx = -5

Анализируя характер изменения поперечной силы на третьем участке, можно заметить, что ее эпюра начинается в отрицательной области значений Q_y, а заканчивается в положительной и, следовательно, пересекает ось абсцисс. Определим координату z* этой точки, приравняв Q_y нулю. Имеем:

Q_y = - P + q z = 0, откуда P = q z и, окончательно, z* = P / q = 1 м.

Поскольку изгибающий момент и поперечная сила связаны дифференциальной зависимостью dM_x/dz=Q_y, а в рассматриваемой нами точке Q_y =0, то изгибающий момент M_x принимает здесь экстремальное значение. Определим его, подставив z* = 1 в уравнение момента на третьем участке:

M_x = - m + P(b + z*) - q z*²/2 = 15 кНм.

и получим третью (промежуточную) точку для построения эпюры M_x .

5. Построим теперь эпюры поперечных сил и изгибающих моментов. Для этого отложим перпендикулярно к оси абсцисс ( для каждой эпюры это линии, параллельные оси балки ) в удобном для пользования масштабе вычисленные значения Q_y и M_x для граничных и промежуточных сечений участков и соединим концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x . При этом положительные ординаты эпюры Q_y будем откладывать вверх, а отрицательные – вниз от оси абсцисс; ординаты же эпюры M_x будем откладывать со стороны растянутых волокон. При вычерчивании параболических участков эпюр изгибающих моментов форма линии эпюры должна соответствовать “правилу паруса”, что применительно к эпюрам, построенным на растянутых волокнах легко интерпретировать графически (см. рис. 3) то есть выпуклость линии эпюры соответствует направлению действия распределенной нагрузки. Знание этого правила особенно полезно при вычерчивании участков эпюр изгибающих моментов по двум точкам.

Рис. 3

После завершения построений на эпюре Q_y нужно проставить знаки, на эпюре же M_x их обычно не ставят ( см. рис. 1, б и 1, в).

Полезно отметить, что из построенных нами эпюр M_x и Q_y теперь можно легко определить численные значения внутренних силовых факторов в заделке (опорную реакцию и момент), не определенные нами в начале решения задачи. Так, из рис. 1, б находим R = +20 кН (↑), а из рис. 1, в – изгибающий момент M_оп = -5 кНм (против часовой стрелке).

6. Проверим теперь правильность построения эпюр M_x и Q_y и их соответствие друг другу. Из зависимости dM_x / dz = Q_y становится очевидным, что порядок линии, описывающей закон изменения изгибающего момента всегда на единицу выше, чем порядок линии, описывающей эпюру поперечных сил. Следовательно, на участках балки между эпюрами внутренних силовых факторов должны существовать следующие зависимости:

Изгибающий момент	Квадратная парабола	Наклонная прямая	Константа
Поперечная сила	Наклонная прямая	Константа	Отсутствует

В местах приложения сосредоточенных нагрузок (сил и моментов) на эпюрах соответствующих им внутренних силовых факторов должны иметь место скачки, равные им по величине. Так, приложенная внешняя сила P будет вызывать скачок на эпюре Q_y , а наличие сосредоточенного момента m будет говорить о скачке на эпюре M_x .

Нелишне еще раз убедиться и в наличие экстремумов на эпюре моментов, а также в соответствии их положений нулевым ординатам на эпюре Q_y.

Как видим, в нашем случае все указанные свойства в эпюрах присутствуют.

7. Построим теперь изображение примерного вида изогнутой оси балки. Поскольку наши построения носят приближенный характер, то основой для проведения такой линии будут являться следующие положения:

Кривизна балки на участках должна соответствовать расположению эпюр изгибающих моментов. Так, если для какого-либо участка эпюра M_x построена на нижних волокнах (в данном случае они растянуты), то кривизна балки должна иметь вид, приведенный на рис.4, а. Если же эпюра моментов расположена на верхних волокнах (теперь они растянуты), то участок балки примет форму, представленную на рис. 4,б.

а) б)

Рис.4

Как видим, на левом рисунке растянуты (удлиняются) нижние волокна, а на правом – верхние.

В точке заделки вне зависимости от величины изгибающего момента поворот сечения отсутствует, следовательно, линия изогнутой оси балки должна выходить под прямым углом (в данном случае, к вертикали).

Участки с разными знаками кривизны упругой линии должны сопрягаться плавной линией (без изломов), а сечение, в котором кривизна меняет знак и которое называется точкой перегиба, должно быть показано на чертеже.

Построенная с учетом вышесказанного упругая линия консольной балки изображена на рис.1, г.

8. Подбор размеров поперечного сечения осуществляем по методу допускаемых напряжений, из которого следует, что в рассмотрение следует принимать лишь то сечение балки, в котором действует наибольший по абсолютной величине изгибающий момент. Однако при этом нужно иметь в виду, что данный прием можно использовать только в случае, когда изгибная жесткость балки EJ_x на всем ее протяжении одинакова, то есть вся балка изготовлена из одного материала и имеет неизменные по своей длине характеристики поперечного сечения. В нашем примере опасным является сечение, в котором M_max = 15 кНм.

9. Прямоугольное сечение деревянной балки подбираем из условия прочности при допускаемом напряжении = 12,4 МПа и заданном соотношении сторон h / b:

,

откуда следует, что требуемый момент сопротивления сечения балки при изгибе должен быть больше или равен:

10. Момент сопротивления прямоугольного сечения относительно нейтральной оси X (см. рис.5, а) будет иметь вид:

.

Для конкретизации расчета предположим, что h / b = 1,5.

Имеем:

,

и, окончательно,

.

При назначении реальных размеров поперечного сечения следует округлить результаты расчетов в большую сторону. Полученные таким образом числовые значения указаны на рис. 5, б.

Рис.5

Схема II. Балка на двух опорах

1. Для определения опорных реакций воспользуемся уравнениями статики. В общем случае для плоской системы нагрузок таких уравнений будет три:

, , .

Записывая, а затем, решая их, получим

V_A = 65 кН, R_B = 105 кН.

Горизонтальная составляющая реакции в опоре А равна нулю, поскольку все внешние нагрузки действуют вдоль вертикали. Направление реакций V_A и R_B указано на рис. 6, а.

Рис.6

2. Как и ранее предполагается, что на всем своем протяжении балка имеет одинаковую изгибную жесткость EJ_x, что выражается в неизменности геометрических размеров сечения по длине балки, а также в постоянстве механических свойств (вся балка изготовлена из одного материала). При этих ограничениях для возникновения каждого нового участка достаточно изменения характера внешней нагрузки (в нашем случае это появление сосредоточенной силы, момента, начало или окончание действия равномерно распределенной нагрузки). Рассуждая, таким образом, устанавливаем, что число участков для нашей расчетной схемы будет равно четырем (рис. 6, а).

3. Проводя последовательно сечения на первом и втором участках, будем рассматривать равновесие правой отсеченной части. При движении слева направо (участки 3 и 4 ) будем рассматривать равновесие левой отсеченной части (рис. 7).

Рис.7

Обход балки с разных сторон целесообразен в тех случаях, когда число участков превышает два. В случае же, если мы будем осуществлять расчет, двигаясь в одном направлении, количество слагаемых от участка к участку будет существенно возрастать, что неизбежно приведет к увеличению объема вычислений.

Имеем:

Для первого участка ( ):

Q_y = + q z₁ (наклонная линия)

M_x = + m - q /2 (квадратная парабола)

Для второго участка ():

Q_y = - R_B + q (a + z₂) (наклонная линия)

M_x = + m - q ( a + z₂ ) ²/2 + R_B z₂ (квадратная парабола)

Для третьего участка ( ):

Q_y = - P (константа)

M_x = - P z (наклонная линия)

Для четвертого участка ( ):

Q_y = - P + V_A (константа)

M_x = - P (d + z₄) + V_A z₄ (наклонная линия)

4. Определим теперь числовые значения Q_y и M_x в характерных сечениях (как и в случае консольной балки, сначала рассмотрим лишь точки, соответствующие началу и концу каждого из участков).

Первый участок:

При z = 0 Q_y = 0 M_x = m

При z = a Q_y = q a M_x = m - q a ²/2

Второй участок:

При z = 0 Q_y = q a - R_B M_x = m - q a ²/2

При z = b Q_y = q (a+b) - R_B M_x = m - q (a+b) ²/2 + R_B b

Третий участок:

При z = 0 Q_y = - P M_x = 0

При z = d Q_y = - P M_x = - P d

Четвертый участок:

При z = 0 Q_y = - P + R_A M_x = - P d

При z = c Q_y = - P + R_A M_x = - P (c+d) + R_A c

Для наглядности вычислим значения ординат при следующих числовых значениях:

a = 1 м, b = 4 м, c = 2 м, d = 2 м, P = 20 кН, m = 5 кНм, q = 30 кН/м и сведем полученные результаты в таблицу:

№ участка	z, м	Qy , кН	Mx , кНм
1 участок	z = 0 z = 1	Qy = 0 Qy = 30	Mx = 5 Mx = -10
2 участок	z = 0 z = 4	Qy = -75 Qy = 45	Mx = 20 Mx = 50
3 участок	z = 0 z = 2	Qy = -20 Qy = -20	Mx = 0 Mx = -40
4 участок	z = 0 z = 2	Qy = 45 Qy = 45	Mx = -40 Mx = 50

Анализируя закон изменения Q_y на втором участке, видим, что эпюра меняет знак. Точка перехода Q_y через ноль даст нам координату экстремума z* (см рис.6, б) на эпюре изгибающих моментов (рис.6, в). Определим эту точку:

Q_y = - R_B + q (a + z) = 0, откуда z* = (R_B – q a) / q = 2,5 м.

Подставляя полученное значение z* в уравнение момента на втором участке, получим величину экстремума, который даст третью (промежуточную) точку для построения эпюры M_x :

M_x = + m - q ( a + z*) ²/2 + R_B z* = 83,75 кНм.

5. По полученным данным (см. табл.) в той же последовательности, что и для консольной балки, строим эпюры поперечных сил и изгибающих моментов (рис.6, б и 6, в).

6. Проведем теперь проверку правильности построения эпюр. Прежде всего, установим соответствие между эпюрами изгибающих моментов и поперечных сил на каждом из участков. Ранее было показано, что порядок линии, описывающей Q_y на единицу меньше, чем порядок линии, описывающей M_x . У нас на первом и втором участках эпюра M_x представляет собой параболу, а эпюра Q_y - наклонную прямую, на третьем и четвертом участках соответственно M_x - наклонная прямая, Q_y - константа. Очевидно, что дифференциальная зависимость dM_x /dz = Q_y на всех участках выполняется. Кроме того, отмечаем, что при Q_y = 0 эпюра моментов имеет максимальное значение (экстремум), что также говорит об удовлетворении указанной дифференциальной зависимости.

Помня о том, что внешние сосредоточенные силовые факторы должны давать на соответствующих им эпюрах скачки, убеждаемся, что под P, V_A, R_B и m действительно есть такие изменения ординат (на 20 кН, 65 кН и 105 кН в эпюре Q_y и 5 кНм - в эпюре M_x ). Таким образом, делаем вывод, что эпюры построены правильно.

7. При вычерчивании изображения примерного вида изогнутой оси балки помимо рассуждений о соответствии её кривизны расположению эпюры моментов (подробности изложены ранее при расчете консольной схемы), отметим также, что в отличие от первого случая здесь имеются две характерные точки (опоры А и В), в которых перемещения равны нулю. Построение обычно начинают с участков, прилегающих к точкам опор (или включающих в себя эти точки). По эпюре моментов делаем вывод, что упругая линия имеет три точки перегиба, комбинируя виды балки изображенные на рис. 4, а и 4, б, сопрягая участки упругой линии в точках перегиба и не забывая при этом, что на опорах перемещения отсутствуют, строим окончательную кривую, представленную на рис. 6, г.

8. Поскольку балка в нашем примере должна быть изготовлена из двутавра, очевидно, что ее поперечное сечение, а также механические свойства по длине остаются неизменными, следовательно, расчет на прочность следует проводить для сечения, в котором действует максимальный изгибающий момент M_x = 83,75 кНм (опасное сечение).

9. Номер двутавра для балки подбираем из условия прочности при изгибе и допускаемом напряжении = 200 МПа (сталь):

,

откуда требуемый момент сопротивления должен быть больше или равен

W_x^тр = 418,75 см³.

10. По сортаменту (ГОСТ 8239-72 Приложение 1) выбираем двутавр № 30 с W_x = 472 см³.

Пример 18.

Для статически определимых систем: схемы I (консольная балка, рис. 1, а), схемы II (двухопорная балка с консолями, рис. 6) при последовательном их рассмотрении требуется:

1. Построить эпюры M_x и Q_y для всех схем и эпюру N_z  для схемы III;

2. Руководствуясь эпюрой M_x , показать на схемах I и II приблизительный вид изогнутой оси балки. По опасному сечению подобрать размеры поперечного сечения:

а) для схемы I - прямоугольное h´b при расчетном сопротивлении R_H =16 кН/м² (клееная древесина); = 1,5;

б) для схемы II - двутавровое (ГОСТ 8239-72) при расчетном сопротивлении R_H = 200 кН/м² (сталь);

Решение.

Схема I. Консольная балка

Учитывая особенности рассматриваемой системы (рис. 1, а), чтобы исключить необходимость определения опорных реакций, достаточно применяя метод сечений, последовательно рассмотреть те отсеченные части системы от заданного сечения, в котором отсутствует опорное сечение.

1. Построить эпюры Q_y и M_x. Для построения эпюр Q_y и M_x определяем количество участков, затем, используя метод сечений, составляем аналитические выражения изменения Q_y и M_x в зависимости от текущей абсциссы z для каждого участка.

Рис. 1

Определение количества участков балки.

Границами между двумя смежными участками, как правило, являются места расположения тех сечений, где происходит скачкообразное изменение: физико-механических характеристик материала конструкций; геометрических характеристик поперечных сечений (формы и/или размеров), а также внешних нагрузок. В данном случае, рассматриваемая балка, имеющая постоянное поперечное сечение (рис.1, б) имеет три участка: участок I - DС, участок II - СВ, участок III - ВА.

Составление аналитических выражений Q_y и M_x и определение значений в характерных сечениях.

Проведя сечение I-I, рассмотрим равновесие правой отсеченной части балки длиной z₁, приложив к ней все действующие справа от сечения заданные нагрузки и внутренние силовые факторы Q_y и M_x , возникающие в сечении, которые заменяют действие отброшенной части балки (рис. 2). При этом, предполагаем, что изображенные на рисунке внутренние силовые факторы положительны.

Составив уравнения равновесия и = 0 для этой части балки и решив их, найдем выражения для и в зависимости от z₁ на участке I ():

,  = 0;

,  кНм.

Полученные выражения показывают, что на участке I и - const. Знак “минус” у говорит о том, что момент в сечении I-I вызывает растяжение верхних, а не нижних волокон, как это показано на рис. 2.

Рис. 2 Рис.3

Участок II ().

Составим уравнения и для отсеченной сечением II-II правой части балки (рис. 3) и определим из них и :

,  , кН;

, + m - P (z₂ - 1) = 0, = -m + P (z₂ - 1) .

Из полученных выражений для и видно, что на участке II величина постоянна, а величина изменяется в зависимости от z₂ по закону прямой линии. Знак “минус” у показывает, что в сечении II-II возникает поперечная сила, действующая в направлении, обратном показанному на рис. 3.

Теперь, подставляя значения z₂ для характерных сечений участка II в полученные аналитические выражения, определим величины и , возникающие в этих сечениях, т.е. ординаты эпюр M_x и Q_y в точках С и В (рис. 1, б).

при z₂ = 1 м; = -30 кН;    = -10 + 30 (1 - 1) = -10 кН×м;

при z₂ = 2 м; = -30 кН;    = -10 + 30 (2 - 1) = 20 кН×м.

Участок III ().

Составим уравнения равновесия и для отсеченной сечением III-III правой части балки (рис. 4) и, решив их, получим,

, → ;

, + m - P (z₃ - 1) + 0,5 q (z₂ - 2)² = 0 = -m + P (z₃ - 1) - 0,5 q (z₂ - 2)² .

Таким образом, величина на участке III изменяется по закону прямой линии, а величина - по закону квадратной параболы.

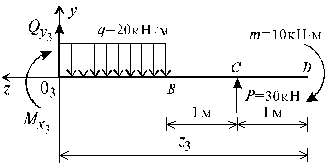
Рис. 4

Подставив значения z₃ , соответствующие характерным сечениям участка, в аналитические выражения изменения и , определим координаты эпюр для сечений В и А (рис. 1, б).

При z₃ = 2 м = -30 + 20×(2 - 2) = -30 кН; = -10 + 30 (2 - 1) - 0,5×20×(2 - 2)² = 20 кН×м.

При z₃ = 4 м = -30 + 20×(4 - 2) = 10 кН; = -10 + 30 (4 - 1) - 0,5×20×(4 - 2)² = 40 кН×м.

Так как, поперечная сила в пределах участка меняет знак, т.е. имеет промежуточное нулевое значение (рис. 1, в), то в этом сечении возникает экстремальное значение изгибающего момента. Для определения его величины вначале найдем значение z₀ , при котором = 0. Для этого, приравняв выражение для нулю, получим:

,    м.

Подставив найденное значение z₀ = 3,5 м в аналитическое выражение изменения , вычислим величину M_max:

кНм.

2.Построение эпюр Q_y и M_x для всей балки.

Отложив перпендикулярно к оси абсцисс (линии, параллельной оси балки) в удобном для пользования масштабе вычисленные значения Q_y и M_x в характерных и промежуточных сечениях каждого участка и соединяя концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x на каждом участке, построим эпюры Q_y и M_x для всей балки (рис. 1, в, г). При этом положительные ординаты эпюры Q_y откладываются вверх, а отрицательные - вниз по оси абсцисс. Ординаты же эпюр M_x откладываются со стороны растянутого волокна. На эпюрах Q_y обязательно указываются знаки, а на эпюре M_x знаки можно не ставить.

Проверка правильности построения эпюр Q_y и M_x.

Рис. 5

Для этого необходимо вначале проверить соответствие эпюры Q_y эпюре M_x согласно дифференциальной зависимости , из которой следует, что эпюра Q_y представляет собой эпюру тангенсов угла наклона касательных эпюры M_x к оси балки. В самом деле, на участке II балки (рис. 1, г) тангенс угла наклона касательной эпюры M_x к оси балки (рис. 5) равен:

При этом, знак поперечной силы будет положительным, если угол образован вращением оси балки или элемента системы по ходу часовой стрелки, и отрицательным, если угол образован вращением этой оси против часовой стрелки до совмещения с эпюрой M_x .

В рассматриваемом примере угол образован вращением оси балки против часовой стрелки, поэтому поперечная сила на этом участке будет отрицательной. После указанной проверки полезно также проверить выполнение следующих положений:

1. Эпюра M_x на участке между сосредоточенными силами, а также между сосредоточенными силой и моментом, и между началом или концом действия равномерно распределенной нагрузки и сосредоточенными силой и моментом всегда изменяется по закону прямой линии, наклонной к оси элемента, а в пределах действия равномерно распределенной нагрузки по закону квадратной параболы, имеющей выпуклость в сторону ее действия, если эпюра построена со стороны растянутого волокна;

2. Под точкой приложения сосредоточенной силы эпюра M_x имеет излом, острие которого направлено в сторону действия силы, если эпюра построена со стороны растянутого волокна;

3. На эпюре M_x в месте действия сосредоточенного момента m имеет место скачок, равный его величине;

4. Над шарнирными опорами двухшарнирной балки изгибающий момент может быть только в тех случаях, когда в опорных сечениях приложены сосредоточенные моменты или когда на консолях, расположенных за опорами, приложены нагрузки. Во всех других случаях изгибающие моменты в шарнирах равны нулю;

5. На участке действия равномерно распределенной нагрузки изгибающий момент достигает экстремального значения M_x = M_max в том сечении, где поперечная сила , т.е. переходит через нуль, меняя знак;

6. Поперечная сила Q_y на участке равна нулю, если во всех сечениях по длине этого участка M_x = const;

7. Эпюра Q_y постоянна на участках между сосредоточенными нагрузками и изменяется по закону наклонной прямой лишь на участках, где действует равномерно распределенная нагрузка;

8. Эпюра Q_y в точках приложения сосредоточенных вертикальных сил (Р, R_A , R_B) имеет скачки, равные по величине приложенным в этих сечениях сосредоточенным силам, причем направление скачков всегда совпадает с направлением этих сил.

В нашем примере все эти положения выполняются.

3. Руководствуясь эпюрой M_x, показать приблизительный вид изогнутой оси балки. При построении приблизительного вида изогнутой оси балки по эпюре M_x необходимо знать, что знак изгибающего момента связан с характером деформации балки от действия заданной внешней нагрузки. Если на участке балки изгибающий момент положителен, то балка на этом участке изгибается выпуклостью вниз, а если отрицателен - выпуклостью вверх. В тех же сечениях, где изгибающий момент равен нулю, кривизна балки меняет свой знак, т.е. ось балки в этих сечениях имеет точки перегиба. При этом всегда следует помнить, что прогибы балки на опорах равны нулю.

Анализируя эпюру M_x (рис. 1, г), видим, что на участке АО растянуты нижние волокна, значит, на этом участке изогнутая ось балки будет иметь выпуклость вниз. На участке ОД растянуты верхние волокна, поэтому изогнутая ось балки на этом участке будет иметь выпуклость вверх. Таким образом, под точкой О, где M_x = 0, кривизна изогнутой оси балки меняет знак, т.е. упругая линия имеет в этом сечении точку перегиба. Учитывая это, строим приблизительный вид изогнутой оси балки (рис. 1, д).

4. Подбор поперечного сечения балки. Опасным сечением является то, в котором возникает наибольший по абсолютной величине изгибающий момент. В нашем примере опасным является сечение Е, где M_max = 42,5 кНм. Прямоугольное сечение балки из клееной древесины подбираем из условия прочности при расчетном сопротивлении R_H = 16 кН/м² и соотношения h/b = 1,5:

,

откуда требуемый момент сопротивления сечения балки при изгибе будет равен:

 м³.

Момент сопротивления прямоугольного сечения равен:

.

Приравняв его , получим = 0,288 м, тогда:

0,192 м.

Округляя, принимаем брус поперечным сечением h´b = 0,29´0,19 м²,

(W_x = 2,663 м³).

Схема II. Двухопорная балка.

1. Построить эпюры Q_y и M_x. Существенное отличие этой схемы (рис. 6, а) от предыдущего примера расчета (рис. 1, а) заключается в том, что при рассмотрении однопролетной консольной балки, для определения внутренних силовых факторов с применением метода сечений, мы последовательно рассматривали равновесие той части системы, где отсутствовало опорное сечение. Данное обстоятельство позволило без предварительного определения опорных реакций, вычислить значения внутренних усилий. Так как этот прием, в данном случае, нереализуем, поэтому предварительно необходимо определить полную систему внешних сил, которая включает заданную систему и все опорные реакции.

Определение опорных реакций.

При общем случае нагружения в заданной системе возникают три опорные реакции. Однако, учитывая особенности характера нагружения, т.е. все внешние силы направлены по оси y, поэтому можно утверждать, что горизонтальная опорная реакция в опорном сечении А в данном случае равна нулю. Вертикальные опорные реакции могут быть определены из условий ;   .

Необходимым и достаточным условием проверки правильности определения вертикальных опорных реакций является , т.к. это уравнение статики, применительно к рассматриваемой системе, которое содержит все искомые опорные реакции.

Из получим:

,

откуда

кН.

Из уравнения будем иметь:

;   R_A = 40 кН_.

Опорные реакции R_A и R_B получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями. После определения опорных реакций следует провести проверку правильности их вычисления.

Рис. 6

; 0 = 0.

Удовлетворение этого уравнения говорит о правильности вычисления величин и направления опорных реакций.

Определение количества участков.

Учитывая, что границами участков являются точки приложения внешних сил и опорных реакций, а также сечения, где распределенная нагрузка меняется скачкообразно. Поэтому заданная балка имеет четыре участка: I участок - КА; II участок - АС; III участок - СВ и IV участок - ВD (рис. 6, б).

Составление аналитических выражений Q_y, M_x и определение значений их в характерных сечениях каждого участка.

Поместив начало системы координат в центре тяжести крайнего левого поперечного сечения балки, и рассекая ее в пределах участка I, рассмотрим равновесие левой части балки длиной z₁ (рис. 7, а). Составив уравнения равновесия и для этой части, найдем аналитические выражения изменения Q_y и M_x на участке I, где z₁ изменяется в пределах :

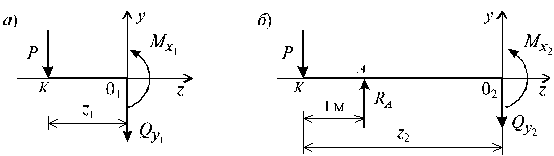
Рис. 7

, -- P = 0,    = -P (постоянная величина);

, -- P×z₁ = 0,    = -P×z₁ (уравнение прямой линии).

Знак “минус” у говорит о том, что в этом сечении возникает поперечная сила, действующая в направлении, обратном показанному на рис. 7, а, а у - что в сечении будет возникать изгибающий момент, растягивающий верхние волокна, а не нижние, как показано на рис. 7, а. Для определения величин и в характерных сечениях этого участка подставим значения z₁ в полученные аналитические выражения:

при z₁ = 0, = -10 кН, = -10×0 = 0;

при z₁ = 1 м, = -10 кН, = -10×1 = -10 кНм.

Проведя сечение в пределах участка II, рассмотрим равновесие левой отсеченной части балки (рис. 7, б) и из уравнений равновесия и найдем аналитические выражения для и на этом участке, где z₂ изменяется в пределах :

,    -- P + R_A = 0,    = R_A - P (постоянная величина);

, -- P×z₂ + R_A (z₂ - 1) = 0, = R_A (z₂ - 1) - P×z₂ (уравнение прямой линии).

Подставив в полученные выражения значения z₂ , соответствующие граничным сечениям участка II, определим величины и , возникающие в этих сечениях:

при z₂ = 1 м, = 40 - 10 = 30 кН, = 40×(1 - 1)-10×1 = -10 кНм;

при z₂ = 3 м, = 30 кН, = 40×(3 - 1) - 10×3 = 50 кНм.

Сделав сечение в пределах участка III, составив и решив уравнения равновесия и для левой отсеченной части (рис. 8), получим аналитические выражения изменения Q_y и M_x на участке III, где z₃ изменяется в пределах :

, -- P + R_A - q×(z₃ - 3) = 0, = R_A - P - q×(z₃ - 3) -уравнение прямой;

, ,

- уравнение параболы.

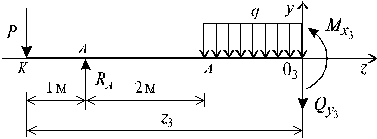
Рис. 8

Теперь найдем и в граничных сечениях С и В участка III:

при z₃ = 3 м, = 40 - 10 - 20×(3- 3) = 30 кН, = 40×(3 - 1)-10×3 - = -50 кНм;

при z₃ = 7 м, = 40 - 10 - 20×(7 - 3) = -50 кН, = 40×(7 - 1) - 10×7 -= 10 кНм.

Как видно, поперечная сила на этом участке принимает в некотором сечении нулевое значение и меняет знак при прохождении через него (рис. 6, в). Поэтому в сечении, где = 0, будет экстремальное значение изгибающего момента. Для его определения найдем величину z₀ , при котором = 0. Приравняв выражение для к нулю, получим:

R_A -P - q×(z₀ - 3) = 0,     м.

Подставив найденное значение z₀ = 4,5 м в выражение для , найдем величину экстремального значения изгибающего момента на этом участке M_max = 72,5 кНм.

Для получения аналитических выражений изменения Q_y и M_x на участке IV целесообразно начало координат перенести в сечение D и рассматривать равновесие правой отсеченной части, т.к. в этом случае вследствие меньшего количества внешних сил, приложенных к правой части балки, аналитические выражения будут проще по своему виду, а вычисление ординат менее трудоемко.

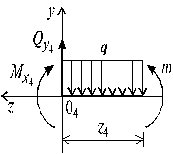
Рис. 9

Аналитические выражения и на участке IV (рис. 9) () получим из следующих уравнений:

, -- q×z₄ = 0, = q×z₄ - (прямая линия);

,   ,    - (парабола).

В граничных сечениях D и В участка IV ординаты эпюр Q_y и M_{x :}

при z₄ = 0, = 0, = 20 кНм;

при z₄ = 1 м, = 20×1 =20 кН, кНм.

Так как величина на участке IV изменяется по закону квадратной параболы, то для уточнения ее очертания надо определить ординату эпюры M_x в каком-нибудь промежуточном сечении. Например, при z₄ = 0,5 м, где ордината будет равна:

кНм.

2.Построение эпюр Q_y и M_x для всей балки.

Откладывая перпендикулярно от оси абсцисс в удобном для пользования масштабе значения Q_y и M_x , возникающие в характерных и промежуточных сечениях каждого участка, и соединяя концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x на этих участках, строим эпюры Q_y и M_x для всей балки (рис. 6, в, г).

3. Руководствуясь эпюрой M_x показать приблизительный вид изогнутой оси балки. Анализируя эпюру M_x (рис. 6, г) видим, что на участке КО растянуты верхние волокна, и поэтому на этом участке изогнутая ось балки будет иметь выпуклость вверх. На участке ОD растянуты нижние волокна, и изогнутая ось балки будет иметь выпуклость вниз. Вследствие этого под т. О, где M_x = 0, будет точка перегиба. Учитывая все сказанное и то, что прогибы в опорных сечениях равны нулю, строим приблизительный вид изогнутой балки (рис. 6, д).

3. Подбор поперечного сечения балки. Опасным является сечение Е, где возникает наибольший по абсолютной величине M_max = 72,5 кНм. Двутавровое сечение балки подбираем из условия прочности при изгибе при расчетном сопротивлении материала R_H = 200 кН/м² (сталь):

.

Откуда требуемый момент сопротивления W_x равен:

м³ .

По сортаменту (ГОСТ 8239-72) принимаем двутавр № 27 с W_x = 37,1 м³. В этом случае при проверке прочности получается недонапряжение, но оно будет меньше 5, что допускается СНиП при практических расчетах.

Пример 19.

Для балки (рис. а) определить из расчета на прочность номер двутаврового сечения, размеры поперечного сечения в форме а) круга диаметром d; б) кольца с отношением диаметров ; в) прямоугольника с отношением сторон . Материал сталь 20, . Составить таблицу отношений площадей указанных сечений к площади двутаврового сечения.

Решение.

Опасным сечением балки является сечение, в котором изгибающий момент достигает наибольшего по абсолютной величине значения. Для этого строится эпюра . Из эпюры, построенной для балки (рис.1), видно, что = 4,16 кНм. Используя условие прочности, находим осевой момент сопротивления

По таблице приложения для двутавра №10 . Выбираем двутавр №10. В соответствии с требуемой из условия прочности величиной осевого момента сопротивления определяем размеры поперечных сечений:

а) для круга ; ;

Принимаем

б) для кольца ; ;

Принимаем

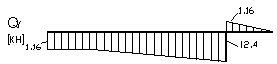
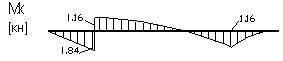
в) для прямоугольника

Принимаем

Таблица отношений площадей

Форма сечений	Двутавр	Круг	Кольцо	Прямоугольник
Площадь сечения	12,0	32,5	16,76	23,12
Отношение площадей	1	2,7	1,4	1,93

Пример 20.

Как выгоднее расположить Т-образное сечение чугунной балки: полкой вверх (рис. а) или полкой вниз (рис. б).

Решение.

Поскольку точка К отстоит от центра тяжести сечения дальше, напряжение в ней по абсолютной величине будет больше, чем в точках L. При указанном направлении силы F растянутые слои балки располагаются сверху. Так как чугун на сжатие работает лучше, чем на растяжение, точку К рациональнее поместить снизу, т.е. следует предпочесть вариант а.

Пример 21.

В некотором сечении балки известен изгибающий момент, равный М_х = -15 кНм. Требуется определить нормальное напряжение в заданной точке К, а также наибольшее нормальное напряжение.

Решение.

Согласно закону распределения нормальных напряжений имеем .

Подставляя I_x = bh³/12 = 6/12 = 500 cм⁴ и y_K = -(5-2) = -3 cм, получим = [-15/(500)] ) = 90 МПа.

Нормальные напряжения пропорциональны расстоянию от нейтральной оси, поэтому

= 90(5/3) = 150 МПа.

Пример 22.

Определить, в каком положении балки квадратного сечения, ее грузоподъемность выше: когда плоскость нагрузки параллельна сторонам квадрата или совпадает с диагональю?

Решение.

Наибольший изгибающий момент равен

и .

Отношение грузоподъемностей

.

Учитывая, что , ,

, ,

получим ,

т.е. в первом варианте грузоподъемность на 41,4 % выше.

Пример 23.

Определить, какой процент экономии металла будет достигнут, если при неизменных прочих условиях применить вместо сплошного круглого сечения кольцевое сечение с отношением диаметров = d_в/d_н = 0,9.

Решение.

Из условия равнопрочности балок или , откуда

. (а)

Отношение весов пропорционально отношению площадей поперечных сечений балок . (б)

С учетом выражения (а) окончательно получим

.

Как видим, экономия достигает 61 %.

Пример 24.

Балки квадратного сечения cоставлены из n пластин, не соединенных между собой. В каком варианте грузоподъемность балки будет больше?

Решение.

Отношение грузоподъемностей балок или, учитывая, что

, ,

получим раз,

т.е. в первом варианте грузоподъемность в n раз больше.

Пример 25.

Определить максимальное напряжение, возникающее в стальной проволоке диаметром d = 0,8 мм при наматывании ее на барабан диаметром D = 50 см.

Решение.

Кривизна связана с изгибающим моментом соотношением =M_x/EI_x, откуда находим изгибающий момент .

Максимальное напряжение .

Учитывая, что , I_x/W_x = y_max = d/2, получим

=Ed/D = 200/500 = 320 МПа.

Пример 26.

Тонкая стальная полоса, имеющая поперечное сечение размером 0,8х25 мм и длину l = 25 см, изгибается сосредоточенными моментами, приложенными на концах, в дугу окружности, опирающуюся на угол , равный 1 радиану. Чему равно максимальное напряжение в полосе?

Решение

Изгибающий момент связан с кривизной соотношением = M_x/EI_x, откуда .

Максимальное напряжение

или, учитывая, что и , I_x/W_x = y_max = h/2,

получим = 200/(2) = 320 МПа.

Пример 27.

Шарнирно опертая по концам стальная балка с поперечным сечением из двух швеллеров №20а нагружена, как показано на рисунке. Определить величину допускаемой нагрузки q, если а = 1 м, = 150 МПа.

Решение.

1. Построение эпюр Q и М.

Опорные реакции:

, R_Aa =qaa + 2qa² - 2qaa- qa, R_A = 2qa;

, R_Ba = qaa + 2qa²-qaa + 2qaa, R_B = 2qa.

Проверка

, -R_A+ qa-2qa-qa+R_B = -2qa+4qa-2qa-2qa+2qa = 0.

Эпюры Q и М строим по характерным точкам.

Расчетный изгибающий момент М_max = 2qa².

2. Определение допускаемой нагрузки.

Геометрические характеристики сечения. Из таблиц сортамента согласно ГОСТ 8240-72 имеем для швеллера № 20а:

I_x = I_y = 139 cм⁴; А = 25,2 см²; z_o = 2,28 cм; b = 8 см.

По формуле параллельного переноса осей момент инерции сечения относительно центральной оси х равен I_x=2[+(b-z_o)²A], откуда момент сопротивления

W_x = I_x/y_max = 2[+(b-z_o)²A]/b = 2[139+(8-2,28)²]/8 = 241 см³.

Из условия прочности балки М_max/W_x = 2qa²/W_x £,

oткуда = W_x /2a² = 150/(2) = 18 кН/м.

Пример 28.

Подобрать необходимые размеры поперечного сечения балки, составленной из двух скрепленных бревен, если q = 26 кН/м, = 10 МПа, Q = 1 м.

Решение.

1. Построение эпюр Q и М.

Опорные реакции:

, R_Aa = 0,5qа² + 2qaa - q×aa, R_A = qa;

, R_Ba = q×aa + 2qaа - 0,5qа², R_B = 2qa.

Проверка

, R_A + R_B - 2qa - q = qa + 2qa - 2qa - qa = 0.

Строим эпюры q и М и находим расчетный изгибающий момент, равный М_max = 1,5 qa².

2. Подбор сечения балки.

Геометрические характеристики. Сечение балки является составным, поэтому

I_x = 2(+y²A) = 2[d⁴/64+(d/2)²d²/4] = (5/32) d⁴,

W_x = I_x/y_max = I_x/d = (5/32)d³.

Из условия прочности балки

M_max/W_x ; 1,5qa²/(5d³/32).

Отсюда .

Пример 29.

Тензометр Т, установленный на стальной балке, имеет коэффициент увеличения k = 1000 и базу s = 20 мм. Показание тензометра равно = 5 мм. Определить наибольшее нормальное напряжение в балке.

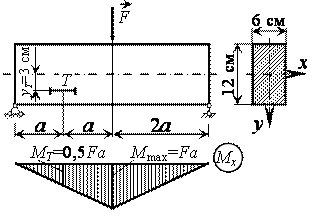
Решение.

Напряжение в балке на уровне тензометра Т равно, с одной стороны,

= Е= Е/(k), (a)

C другой стороны, = (M_T/I_x) . (б)

Наибольшие нормальные напряжения возникают в крайних волокнах того же сечения, где приложена сила F, т.е.

. (в)

Разделив (в) на (б), получим = (M_max/М_Т)(y_max/y_Т) = 4 или с учетом (а)

= 4Е/(k) = 4/(1000) = 200 МПа.

Пример 30.

Тележка перемещается вдоль балки длиной l = 10 м. На каждое колесо действует нагрузка F = 20 кН. Найти опасное положение тележки, при котором изгибающий момент будет иметь наибольшее значение и определить наибольшее напряжение, полагая С = 2 м.

Решение.

Очевидно, наибольший изгибающий момент возникает в сечении, расположенном под передним колесом тележки (сеч. D), где

M_D = R_B(l – z - C) = F(2z + C)(l – z -C)/l,

R_B = F(2z + C)/l.

Из условия экстремума dM_D/dz = 0 находим опасное положение тележки

,

z⁴ = (2l-3c)/4.

В нашем случае z^* = (2- 3)/4 = 3,5 м.

Наибольший изгибающий момент

M_max = M_D(z^*) = F(2z^* + c)(l - z^* - c)/l,

M_max = 20(2 + 2)(10 - 3,5 - 2)/10 = 81 кНм.

Максимальное напряжение

= M_max/W_x = 81/953 = 85 МПа.

Пример 31.

Определить касательное напряжение в точке К данного сечения, если поперечная сила равна Q = 500 кН.

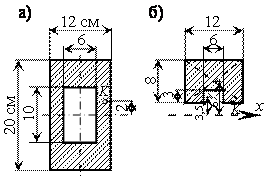
Решение.

По формуле Журавского имеем .

Учитывая, что b_K = 6 см,

,

получим .

Пример 32.

Определить главные напряжения в точке К консольной балки (рис.1), нагруженной сосредоточенной силой F = 50 кН, приложенной на свободном конце, если l = 50 см, С = 20, d = 4 см, b = 4 см, h = 10 см.

Рис.1

Решение.

1. Определение внутренних силовых факторов в поперечном сечении, проходящем через точку К. Строим эпюры Q_y и M_x и находим Q_K = -F = -50 кН,

M_K = -F×C = -50 = -10кН×м.

2. Определение главных напряжений. Напряжения в поперечном сечении определяются по формулам

,

.

Вычисляя ,

,

,

, находим

,

.

Величины главных напряжений

;

; ; .

Направление главного растягивающего напряжения по отношению к продольной оси балки z:

; ,

а напряжение направлено перпендикулярно к .

Графическое определение величин главных напряжений и направлений главных осей представлено на рис. 2.

Рис. 2

Онлайн-калькулятор "Подбор круглого сечения балки при изгибе"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00