Главная
Тема 5. Кручение
прямого стержня
Формула для угла закручивания круглого стержня была впервые экспериментально установлена Ш.Кулоном.
В мемуарах, представленных в Парижскую академию наук в 1784 г. [353], Ш.Кулон привел результаты экспериментального исследования крутильных колебаний круглого стержня, получил дифференциальное уравнение свободных крутильных колебаний и вывел формулу для периода колебаний. Исследуя крутильные колебания экспериментально на специальном приборе, Кулон установил, что при малых углах закручивания период не зависит от угла закручивания. На этом основании Кулон сделал правильный вывод о том, что угол закручивания пропорционален крутящему моменту.
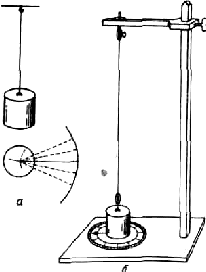
Установка для исследования крутильных колебаний Ш.Кулона
Испытывая на кручение круглые проволоки различной длины и различного диаметра, Кулон экспериментально получил правильную формулу для угла закручивания круглого стержня длиной l:

где M — крутящий момент, k — постоянная для материала. В настоящее время мы знаем, что

где G — модуль упругости при сдвиге. Таким образом, Кулон ввел понятие модуля упругости при сдвиге и экспериментально определил его для железа и латуни. Кулон понимал, что линейная зависимость угла закручивания от крутящего момента справедлива только в начальной стадии нагружения, и экспериментально определил величины крутящих моментов, превышение которых приводит к остаточной деформации. Кроме этого, он установил, что предварительное закручивание за пределы упругости (наклеп) и последующая разгрузка увеличивают пределы линейной зависимости между крутящим моментом и углом закручивания в случае закручивания в ту же сторону, что и предварительное.
На пропорциональность касательного напряжения расстоянию от центра поперечного сечения круглого стержня было указано Т.Юнгом в 1807г. в его курсе лекций [506].
Это положение, справедливое только для круглого поперечного сечения, было ошибочно распространено Л.Навье в упомянутой выше книге [447] на другие формы поперечных сечений, в результате чего были получены неверные формулы.
Они не подтверждались в экспериментах французского инженера Альфонса Жана Клода Буржуньона Дюло (DuleauA.J. K. B.), результаты которых были приведены в его книге, изданной в 1820 г. [357]. Дюло испытывал на кручение железные стержни круглого кольцевого и прямоугольного поперечных сечений. Для круглых и кольцевых сечений А.Дюло подтвердил результаты, полученные Ш.Кулоном. Однако он установил, что в случае прямоугольного сечения предположение о пропорциональности касательного напряжения расстоянию от оси стержня неверно. Этот результат удивил Л.Навье. Несмотря на это, в первом издании своей книги он изложил неверное решение и только во втором издании признал, что гипотеза плоских сечений не совсем точна и привел (тоже неверное) решение О.Коши.
О.Коши понимал, что поперечные сечения
стержня некруглого поперечного сечения при кручении не остаются плоскими —
происходит депланация сечений. Однако, по мнению Коши, это имеет место только
для сечений, у которых главные осевые моменты инерции не равны между собой.
Таким образом, Коши считал, что для такого сечения, как правильный
многоугольник, закон плоских сечений справедлив, что конечно, неверно. При решении
задачи кручения стержня прямоугольного поперечного сечения, изложенном в
статье, опубликованной в 1830 г. [341], Коши исходил из уравнения

где W — перемещение точек поперечного сечения
вдоль оси стержня, x, y — координаты точек поперечного сечения, I1,
I2 — главные осевые моменты инерции поперечного сечения, θ
— относительный угол закручивания. В результате для прямоугольного сечения со
сторонами a и b Коши получил формулу
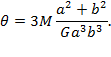
Интересно отметить, что для узкого прямоугольника (a>>b) эта формула дает правильный результат. Впрочем, через четверть века в 1854г. О.Коши признал свое решение неверным.
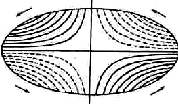
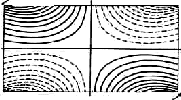
Основные уравнения задачи кручения призматического стержня произвольного поперечного сечения были получены методами теории упругости Б.Сен-Венаном в мемуарах, представленных в 1853г. в Парижскую академию наук и опубликованном в 1855 г. [255]. Краткое изложение мемуаров было дано в статье, вышедшей в свет в 1853г. [476] Б.Сен-Венан развил так называемый полуобратный метод, согласно которому задают некоторые компоненты перемещений и напряжений, а недостающие определяют так, чтобы удовлетворялись все уравнения теории упругости и граничные условия. Им был рассмотрен ряд частных случаев поперечных сечений: эллиптическое, правильный треугольник и прямоугольник. Для первых двух сечений решения получены в замкнутой форме. В третьем случае прямоугольного сечения Б.Сен-Венан решил задачу в рядах и подсчитал коэффициенты для определения напряжений в серединах сторон прямоугольника и угла закручивания. Б.Сен-Венан исследовал также депланацию некруглых поперечных сечений; на рисунках представлены горизонтали депланированного поперечного сечения в случаях, если оно является эллипсом и прямоугольником, полученные Сен-Венаном [255].
В 1871г. Сен-Венан опубликовал решение задачи об упруго-идеальнопластическом (без упрочнения) кручении круглого стержня [254].
Экспериментальный метод решения задачи кручения стержня на основе так называемой мембранной аналогии был предложен Л.Прандтлем в 1903г. [467], а подсчет предельного крутящего момента при помощи аналогии с песчаной насыпью А.Надаи [442] и одновременно с ним математиком и механиком Эрихом Треффтцем (TrefilzE., 21.02.1888 — 21.01.1937) [488] в их докладах на съезде по прикладной механике в Марбурге (Германия) в 1923г.
Изложение решений большого количества задач кручения однородных и неоднородных тел постоянного и переменного сечений в пределах пропорциональности приведено в капитальной монографии Н.Х.Арутюняна и Б.Л.Абрамяна [120].
Общее решение задачи о кручении стержня, в том числе и составного, из различных материалов, при помощи теории функций комплексного переменного дано в работах Н.И.Мусхелишвили и изложено в его монографии [213], первое издание которой вышло в 1933.
Впервые теорию функций комплексного переменного к решению плоской задачи теории упругости применил Г.В.Колосов в 1908-1909 гг. [410, 189].
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов