Главная
Тема 23. История развития механики деформируемого
твердого тела
История хранит много примеров уникальных
строительных сооружений, выполненных человеческими руками. В Египте на Ниле
была возведена Асуанская ирригационная система с плотинами, водохранилищами,
каналами. В Китае в V1 веке до н.э. реки Хуанхэ и Янцзы были соединены Великим
каналом протяженностью свыше 1000 км. Три тысячи лет назад человек строил
крепости, дворцы, дороги, храмы, театры, стадионы.
Искусство античных зодчих
достигало совершенства. Как венец творения человеческих рук возвысились над
древним миром семь чудес света: статуя Зевса в Олимпии, висячие сады Вавилона,
мавзолей в Галикарнасе, Колосс Родосский, маяк в Александрии, храм Артемиды в
Эфесе и египетские пирамиды. Античная строительная техника достигла больших
высот. В IV веке до н.э. уже применялся известковый раствор, в III веке до н.э.
– пуццолановый раствор из измельченной породы вулканического происхождения. На
основе этого раствора вскоре появился бетон. В Китае с IV века до н.э. начала
строиться Великая Китайская стена протяженностью 4000 км и шириной 10 м, по
верху которой передвигались колонны войск с повозками.
Создания зодчих Древнего
Востока поражают не только размерами и гармонией, но и сочетанием
архитектурного решения сооружения с его функциональным назначением. Расцвет
архитектурного искусства в Древней Греции, а затем в Риме привел к зарождению
теории архитектуры и строительного искусства.
Одним из первых теоретиков
строительства принято считать римского архитектора и инженера второй половины
I века до н.э. Марка Витрувия. Его фундаментальный
труд "Десять книг об архитектуре" представляет собой подлинную
энциклопедию строительного дела. Очень многие рекомендации Витрувия
и сейчас звучат в высшей степени современно. И все же, хотя проблема прочности
существовала всегда, хотя человечество имело уже тысячелетний опыт
строительства, теории строительной механики не существовало. Поиск прочности
происходил пока еще интуитивно. Методом многочисленных проб и ошибок шел человек
к познанию тайн материала. Это познание начиналось с анализа причин разрушения.
Восхищаясь сооружениями
античных мастеров, нам следует помнить о том, что сроки строительства всегда
были неимоверно высоки. Возведение одного храма или дворца длилось десятки, а
иногда и сотни лет. При этом строительство обходилось очень дорого, с затратой
огромного количества ценнейших материалов, при неограниченной эксплуатации
рабского труда. Наконец, и это менее известно, строящиеся сооружения часто
разрушались, и строители учились на уроках аварий. В этом плане поучительно разрушение
амфитеатра в Фидене в 27 году н.э. Даже в самых
современных сооружениях древних можно найти грубые сшибки, свидетельствующие о
незнании ими основ сопротивления материалов, строительной механики и теории
сооружений. Другая серьезная причина разрушений – землетрясения. И храм
Артемиды, и Галикарнасский мавзолей, и Родосский Колосс простояли бы гораздо
дольше, если бы строители наряду с гибким основанием обеспечили бы
пространственную жесткость конструкций. Сооружения нужно было рассчитывать на
ветровую нагрузку и устойчивость, в связи с чем фундаменты и основания выполнять
с учетом работы их на опрокидывание в сочетании с сейсмическими условиями.
Нужно отметить, что недостаток знаний о прочности в строительстве часто
ограничивал зодчих в выборе архитектурных форм. Повальное увлечение античных
архитекторов колоннадами возникло отнюдь не только из эстетических соображений,
а еще и потому, что не было материалов, работающих на изгиб для перекрытия
больших пролетов. Достаточно сказать, что самая длинная балка, перекрывающая
вход в Акрополь, была длиною менее 4 м, а самая длинная плита – над усыпальницей
в пирамиде Хеопса – немногим более 5 м. Поэтому и приходилось ставить колонны
близко друг к другу. И лишь позже уже римляне изобрели такие конструкции, как
арки и своды, в которых камень работает на сжатие, что позволило увеличить
пролеты, а также изменить облик сооружений.
Аварии происходили не
только в древние и средние века, они продолжались (конечно, в меньшем
количестве) вплоть до нашего времени. Каждая авария возбуждала у специалистов
потребность в новом поиске, ставила новые задачи, прибавляла новые знания.
Когда же знаний не хватало, в инженерные расчеты вводили (и вводят сейчас) так
называемый коэффициент запаса. Поначалу расчет производили весьма приближенно.
Определяли нагрузку, которую должен был выдержать элемент при эксплуатации, и
подбирали такие его размеры, которые позволили бы выдержать нагрузку, большую
эксплуатационной, скажем, в 100 раз. Это значит, что у создаваемого элемента коэффициент
запаса равен 100. По мере развития науки этот коэффициент уменьшается все
больше, уступая место точным численным величинам, характеризующим то или иное
открытое явление, тот или иной процесс в материале, элементе, конструкции,
сооружении. Потребность уменьшить коэффициент запаса диктовалась многими
факторами. Со временем исчезла дешевая рабочая сила, которую можно было
эксплуатировать безгранично. Возникла необходимость экономить материальные
средства и ресурсы. Чтобы строить дешевле, с меньшими трудовыми и
материальными затратами, потребовались поиски резервов в материале, в формах
конструкции, технологии строительства. В авиации и космонавтике большие запасы
прочности связаны с большим весом летательных аппаратов, а, следовательно, с
меньшей полезной нагрузкой. Следовательно, запасы прочности должны быть как
можно меньшими, тогда строить можно будет быстрее, дешевле, с большей
экономической отдачей. По сути дела, вся история науки о прочности была
историей борьбы за уменьшение коэффициента запаса прочности. Сейчас этот
коэффициент стал весьма небольшой величиной (от полутора до трех). Но для этого
понадобились века.
Полторы тысячи лет прошло
со времени исчезновения с лица земли шести из семи чудес света, когда
итальянский художник и ученый эпохи Возрождения Леонардо да Винчи (1452-1519)
начал эксперименты по изучению прочности материалов. Леонардо да Винчи был не
только замечательным художником, но и талантливым механиком, математиком и
инженером, которому обязаны важными открытиями самые разнообразные отрасли
науки и техники.
С опытов Леонардо начался
экспериментальный период в развитии строительной механики. Леонардо был
неутомимым экспериментатором. Производя многочисленные опыты, он фиксировал все
в своих записных книжках. Вызывает удивление тщательность, с которой
описывались условия и технология проведения экспериментов. Леонардо испытывал
на изгиб балки на двух опорах, консольные балки, колонны. Он пришел к выводу,
что "несколько малых опор, соединенных вместе, выдержат больший вес, чем, если
они будут разделены". Леонардо да Винчи провел интересные опыты на
растяжение металлических проволок, струн, различных волокон. Он сконструировал
оригинальное приспособление для определения сопротивления железной проволоки
разрыву. Конечно, не все выводы Леонардо правильны, есть в них противоречия,
ошибки. Поэтому вряд ли можно говорить о значительной практической или теоретической
ценности этих опытов. Однако они имеют немалое значение для истории механики,
которое состоит в том, что впервые поиск прочности твердых деформируемых тел
приобрел форму сознательного, специально заданного исследования.
Новый значительный шаг в
развитии представлений о прочности через 120 лет после Леонардо да Винчи
суждено было сделать еще одному титану эпохи Возрождения – Галилео Галилею
(1564-1642). Великий итальянский физик, механик и астроном Галилей признан
одним из основоположников естествознания. Известны его работы в области астрономии
(борьба за учение Коперника, а затем отречение от него). Заслужили признания
его работы в области динамики. А вот работы его в области сопротивления
материалов менее известны. Между тем именно Галилей свел большой круг вопросов,
связанных с прочностью и разрушением материалов, в одну область знания. Он
впервые указал на необходимость построения собственной теории, создания
собственной науки – сопротивления материалов. Из своих опытов Галилей сделал
один важный вывод: "Если мы ... построим большую машину из того же самого
материала и точно сохраним все пропорции меньшей, то в силу самого свойства
материи мы получим машину, соответствующую меньшей во всех отношениях, кроме
прочности и сопротивляемости внешнему воздействию: в этом отношении, чем больше
будет она по размеру, тем менее будет она прочна". Это явление, названное впоследствии
масштабным фактором, учитывается и сейчас в расчетах строительной механики. В
действующих стандартах на испытание строительных материалов вводятся переводные
коэффициенты для показателя прочности. Чем меньше лабораторный образец, тем
больше уменьшающий коэффициент надо вводить, чтобы получить необходимую
прочность промышленного элемента или конструкции.
Галилей предлагал
использовать пустотелые элементы. Он заключает, что при сравнении сплошной и
трубчатой балок, имеющих одинаковую площадь сечения, трубчатая будет во столько
раз прочнее, во сколько раз диаметр трубы больше диаметра сплошной балки.
Галилей изучал только два вида деформации – растяжение и изгиб на всевозможных
элементах из различных материалов, объясняя причины их прочности и разрушения.
Нужно отметить, что Галилей во всех случаях изучал состояние материалов в
момент разрушения. Прочность, по Галилею, была связана с критическим,
предельным состоянием балки. Ученый пытался понять, почему колонна или балка
разрушается, какая сила вызывает это разрушение. Поведение же нагруженного
элемента в нормальном рабочем состоянии, физико-механические процессы,
происходящие при обычных нагрузках, были Галилею неведомы. Галилей пытался
выйти за рамки умозрительных рассуждений и прийти к теоретическому обобщению.
Но для этого ему не хватало математического аппарата и данных теоретической
механики. Поэтому нельзя сказать, что он построил теорию, но он подготовил почву,
на которой в дальнейшем выросла первая теория прочности.
Немногим позднее вопросами
прочности твердых тел занимался французский ученый Эдм
Мариотт (1620-1684). При проектировании Версальского дворца он проводит
большие эксперименты по растяжению и изгибу самых различных материалов.
Мариотт, изучая прочность деревянных и стеклянных балок, проверил результаты
Галилея и убедился в их справедливости. Испытывая балки, заделанные жестко
двумя концами, он обнаружил, что прочность таких балок увеличивалась вдвое по
сравнению со свободно опертыми балками. Опытами Мариотта заканчивается первый, экспериментальный
период изучения сопротивления материалов. Результаты научных поисков этого
периода принесли огромную пользу и не утратили своего значения до сих пор.
Наука набирала темпы, росло
число ученых, возникла потребность в общении их друг с другом, в обсуждении
научных проблем. В разных странах Европы организуются научные общества: в
Италии, Англии, Франции, позже России и Германии. В 1662 году в Лондоне было
официально открыто знаменитое Королевское общество, в число членов которого (по
рекомендации известного английского физика и химика Роберта Бойля) был принят
Роберт Гук (1635-I703).
Гук был талантливым
механиком, он создал немало приборов, механизмов, приспособлений. Его
исследования были настолько разносторонни и многогранны, что неизбежно вторгались
в сферы деятельности других ученых, работавших на передовых рубежах науки.
Поэтому часты были случаи cпopoв Гука за свой
приоритет, например с И. Ньютоном. И только один закон по праву носит его имя и
принадлежит ему без всякой конкуренции. Это закон упругости материальных тел,
известный под названием закона Гука. Суть его можно выразить в трех словах:
"Деформация
пропорциональна нагрузке", или, как записал Гук в своей криптограмме:
"Каково удлинение, такова и сила". Этот закон был выведен Гуком в
1676 году после проведения ряда экспериментов, а именно: а) удлинения железной
проволоки; б) растяжения винтовой пружины; в) сокращения спиральной часовой
пружины; г) изгиба балки, закрепленной одним концом и нагруженной на другом
конце. Убедившись во всех опытах в действии своего закона, Гук признал его
всеобщим.
Чтобы понять сущность
закона Гука, обратим внимание на исследования Ньютона, который так
сформулировал его в качества основного (третьего) закона механики: действие
равно противодействию по величине и противоположно ему по направлению. Это
означает, что каждая сила, воздействующая на тело, должна быть сбалансирована
точно такой же по величине силой противоположного направления. При этом природа
сил не имеет никакого значения. Задача любой механической конструкции состоит в
сохранении её целостности, для ее выполнения в конструкции должны каким-то
образом возникать силы, которые могли бы уравновесить внешние нагрузки,
действующие на нее. Причем, прежде чем начать сопротивляться внешним нагрузкам,
в твердых телах должны возникнуть какие-то смещения, то есть, чтобы оказать
какое-либо сопротивление, они должны в большей или меньшей степени поддаться
нагрузке. Под смещением понимается не перемещение тела как целого, без
изменения его формы, а именно геометрические искажения самого тела, т.е. тело в
целом или отдельные его части становятся короче или длиннее вследствие
растяжения или сжатия внутри самого тела. В природе не существует абсолютно
жесткого материала, все тела в той или иной мере обладают податливостью. Ветки
деревьев под тяжестью прогибаются на значительную величину, а прогиб мостов под
тяжестью передвигающихся по ним грузов настолько мал, что незаметен
невооруженным глазом. Но как смещения ветвей, так и отклонения моста могут быть
охарактеризованы количественно. Пока смещения, вызванные внешними нагрузками,
не слишком велики и не мешают конструкции выполнять свои задачи, они
определяют обязательные характеристики конструкции. Кто летал самолетом, может
быть замечал, как смещаются вверх-вниз концы его крыльев. Конструктор специально
наделил при проектировании крыла его такими свойствами. Ясно, что смещения,
будь они малыми или большими, создают силы сопротивления. Эти силы определяют
жесткость твердого тела, его способность сопротивляться внешним нагрузкам.
Другими словами, в твердом теле возникают именно такие смещения, которые как
раз достаточны, чтобы уравновесить приложенные внешние нагрузки. Это происходит
совершенно автоматически.
Как же возникают эти силы?
Дело в том, что в любом теле атомы химически связаны между собой. Эти связи
условно можно представить в виде пружинок, хотя, конечно, ничего
"твердого" в обычном смысле этого слова в промежутках между атомами
не существует (рис. 1).
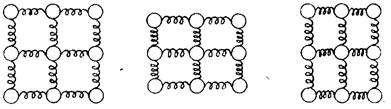
а)
б) в)
Рис. 1
Те же силы, которые делают тело твердым,
определяют и его химические свойства. Разрушение химических связей освобождает
энергию пороха и бензина, те же связи делают резинку и сталь упругими и
прочными. Когда твердое тело полностью свободно от механических нагрузок (что
бывает, строго говоря, очень редко), химические связи, или пружины в нашей
модели, находятся в нейтральном положении (рис.1,а).
Любая попытка сблизить
атомы (это мы называем сжатием) или оттянуть их друг от друга (что обычно
называется растяжением) сопровождается небольшим укорочением или удлинением
межатомных пружин во всем объеме металла (рис. 1, б, в). При этом ядра атомов
считаются жесткими, кроме того, в твердом теле атомы обычно не обмениваются
местами, по крайней мере при умеренных, или "безопасных" нагрузках.
Таким образом, податливость твердого тела определяется межатомными связями.
Жесткость этих связей может изменяться в широких пределах, но для большинства
веществ она намного выше, чем у тех металлических пружин, с которыми мы
встречаемся в повседневной жизни. Очень часто величины межатомных сил весьма и
весьма велики, что и следует ожидать, если вспомнить о силах, которые могут
быть получены при разрыве химических связей горючих или взрывчатых веществ.
Хотя абсолютно жестких тел, т.е. таких, которые под действием внешних сил
совершенно не изменяют своей формы, в природе не бывает, смещения во многих
предметах часто оказываются очень малыми. Так, например, высота обычного
строительного кирпича под нагрузкой 80 кг уменьшается примерно на 0,5∙10-4
см. При этом два любых соседних атома в кирпиче станут ближе один к другому на
расстояние 2∙10-14 см или
0,2∙10-5 Å
(один ангстрем Å = 10-8 см).
Величина эта невероятно мала, но она соответствует совершенно реальным
перемещениям атомов. Конечно, в крупных конструкциях перемещения элементов не
всегда малы. Канаты, на которых висит мост через залив Форт (Шотландия), все
время растянуты примерно на 0,1%, что при их общей длине почти 3 км составляет
около 3 м. В этом случае атомы железа, расстояние между которыми в
ненапряженном состоянии около 2 Å, удаляются на величину
0,2∙10-2 Å.
Опыты показали, что смещения атомов в металлах, например, строго
пропорциональны величине, на которую удлиняется (или укорачивается) весь кусок
металла. В этих экспериментах наблюдались изменения межатомных расстояний
примерно до 1%.
Все эти рассуждения
подводят нас к понятиям "напряжение" и "деформация".
Напряжение – это нагрузка,
отнесенная к единице площади, т.е.
![]()
где σ
– напряжение, Р – нагрузка, F – площадь. Если обратиться к примеру
о строительном кирпиче с поперечным сечением 25х12 см под нагрузкой 80 кг, то
сжимающее напряжение в нем будет σ= 80/300 ≈0,27
кг/см2. Точно такое же напряжение вызовет в кирпичной опоре моста
(сечение 10х6 м) проезжающий по нему локомотив весом 160 т. Следовательно, с
полной определенностью можно сказать, что в обоих случаях напряжения в кирпиче
примерно одинаковы, и если один кирпич не разрушился под тяжестью в 80 кг, то и
опора моста не разрушится под весом локомотива в 160 т.
Напряжение выражается в
кгс/мм2, кгс/см2, Н/м2, Па и т.д.
Деформация – это величина
удлинения стержня под нагрузкой, отнесенная к начальной длине. Очевидно, что
отрезки различной длины при одной и той же нагрузке получают в конструкциях
различное удлинение. Если обозначить деформацию через ε , то
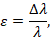
где ∆λ
– полное удлинение, а λ – начальная длина. Так,
если стержень длиною 100 см под нагрузкой удлиняется на 1 см, то его деформация
составляет 1%. Такая же деформация будет у стержня длиной 50 см, растянутого
на 0,5 см и т.д. Деформация, также как и напряжение, не зависит от размеров
образца. Деформация есть отношение удлинения к начальной длине и,
следовательно, она безразмерна. Роберт Гук был первым, кого осенила догадка о
том, что происходит при нагружении твердого тела. Он подробно изучал поведение
часовых пружин и маятников. Ничего не зная, конечно, о химических и электрических
межатомных связях, Гук понял, что часовая пружина всего лишь частный случай
поведения любого твердого тела, что в природе нет абсолютно жестких тел, а
упругость является свойством всякой конструкции, всякого твердого тела. Тогда
Гук и заявил: "Каково удлинение, такова и сила". Иными словами,
напряжение пропорционально деформации, и наоборот. Так, если упругое тело,
например струна, удлиняется на 1 см под нагрузкой 100 кгс, то под нагрузкой
200 кгс удлинение составит 2 см и т.д. Это утверждение и стало известно как
закон Гука. Оно является краеугольным камнем всей техники.
При очень больших
деформациях (скажем 5-10%) от пропорциональности между напряжением и
деформациями не остается и следа. Но обычно деформации не превышают 1%, а в
этом диапазоне зависимость между напряжениями и деформациями линейна. Более
того, для малых деформаций процесс нагрузки и разгрузки обратим, т.е. кусок
материала можно нагружать и снимать с него нагрузку тысячи и миллионы раз с
одним и тем же результатом. Наглядный пример этому – пружинка балансира в
часах, которая повторяет один и тот же процесс (напряжение и снятие нагрузки)
18 тысяч раз в час. Такой тип поведения твердого тела под нагрузкой называется
упругим. В 1678 г. Гук писал: "Сила всякой пружины пропорциональна ее
растяжению, т.е., если сила растянет или согнет пружину на некоторую величину,
то две силы согнут её вдвое больше, три силы согнут втрое больше, и так
далее". В том же 1678 г. вышла из печати работа Гука "О
восстановительной способности или об упругости", содержащая описание ряда
опытов с упругими телами. Это была первая книга по теории упругости, где Гук
отмечает, что независимо от вида нагрузки (растяжения или сжатия) – изменения
размеров тела пропорциональны приложенной силе. Гук проводил много опытов и с
деревянными балками. Изготовив балку из дерева, он измерял ее прогиб под
действием в различных частях балки различных весов. При этом он, например,
пришел и к такому великому выводу о том, что на выпуклой поверхности балки
волокна при изгибе растягиваются, а на вогнутой – сжимаются. Прошло очень много
времени, пока инженерам стало ясно значение этого, как теперь представляется,
очевидного свойства материала.
Итак, деформация
пропорциональна нагрузке, и наоборот. Гук считал, что его закон действует
всегда – при любых нагрузках и в любых материалах. И здесь, в полном
соответствии со своим увлеченным характером, он не довел это исследование до
конца и допустил неточность. Но об этом потом. Современники его не
опровергали: главное, что был сделан очень важный шаг. Был найден основной
закон сопротивления материалов. Рассуждения Леонардо да Винчи и Галилео
Галилея постепенно становились на научную основу, благодаря которой со временем
они будут описаны математическими формами.
Гук установил, что
удлинения, укорочения, прогибы как пружин, так и других упругих тел
пропорциональны приложенным к ним напряжениям. Они зависят, конечно, от
геометрических размеров и формы конструкции, а также от того, из какого
материала она сделана. Мы не знаем, понимал ли Гук, в чем разница между
упругостью как свойством материала и упругостью как функцией формы и размеров
конструкции. Дело в том, что можно получить сходные кривые "нагрузка -
удлинение" и для куска резинового шнура и для стальной пружины (а ведь это
материалы с различными прочностными свойствами). Это сходство явилось
источником бесконечных заблуждений. Примерно столетие после Гука существовала
эта путаница: не всем была ясна разница между двумя понятиями упругости. И это
длилось до тех пор, пока в 1800 г. английский ученый Томас Юнг (1773-1829 гг.)
не пришел к выводу, что если пользоваться не абсолютными значениями сил и
смещений в конструкциях, а напряжениями и деформациями, то закон Гука можно
записать в следующем виде: напряжение/деформация = σ/ε
~
const. Юнг заключил, что эта константа является
неотъемлемой характеристикой каждого химического вещества и представляет его
жесткость. Эта константа упругости называется теперь модулем Юнга Е = σ/ε.
Следовательно, Е описывает жесткость материала как такового. Жесткость любого
заданного объекта зависит не только от модуля Юнга материала, но и от
геометрической формы объекта.
Все встало на свои места, когда
английский ученый Томас Юнг показал, что для каждого материала существует
постоянная величина, характеризующая способность его сопротивляться воздействию
силы. Эта величина и была названа модулем упругости, или модулем Юнга. Юнг заметил,
что сжатие бруса всегда сопровождается его утолщением, а значит, увеличением
площади его поперечного сечения. Растяжение же делает брус или проволоку
тоньше, следовательно, уменьшает площадь сечения.
Рассуждения Юнга начались с
переосмысления закона Гука и его опытов. Если с удвоением нагрузки в проволоке
или пружине удлинение удваивается, а с утроением – утраивается и т.д., то
частное от деления силы на удлинение будет величиной постоянной. Для того
чтобы абстрагироваться от размеров элемента и вида нагрузки, Юнг предложил
использовать не абсолютные, а относительные значения силы и деформации
(удлинения и укорочения). Действующую на элемент силу (растягивающую или
сжимающую) он приводил к единице площади сечения. Немного позднее эта
относительная величина была названа напряжением. Вместо же абсолютной
деформации, например удлинения, Юнг вводит величину относительной деформации,
представляющую собой отношение удлинения, максимально возможного для данного
материала, к первоначальной длине. Другими словами, если относительная
деформация равна единице или 100%, то это значит, что элемент до своего
разрушения способен удлиниться вдвое. При этом имеется в виду, что закон Гука
действует в материале до самого разрушения.
Модуль упругости
характеризует важнейшее свойство конструкционного материала – его жесткость.
Резина, дерево, стекло, сталь обладают различной жесткостью. Модуль упругости
резины равен 70 кгс/см2, для стекла он в 1000 раз больше. Дерево
вдвое жестче стекла, а сталь в 14 раз жестче дерева. Кстати, значение модуля
упругости для стали, равное 2∙106 кгс/см2,
также определил Юнг (правда, в других единицах – фунтах на дюйм). Физический
смысл модуля упругости, который и сейчас не является чем-то очевидным, во
времена Юнга остался непонятным большинству современников. Да и сам Юнг дает
этому понятию не совсем четкое определение. Это был не единственный случай,
когда Юнг недостаточно точно выражал свои мысли. Очевидно, из-за этой своей
черты он не добился больших успехов на педагогическом поприще, но личность его
как ученого представляет большой интерес.
Громадная важность модуля
упругости для техники объясняется двумя причинами. Во-первых, нам нужно точно
знать возникающие под нагрузками смещения как в конструкции в целом, так и в
различных ее частях (т.к. под действием рабочих нагрузок взаимодействие деталей
в конструкции не должно нарушаться, а в таких расчетах и нужны в первую
очередь величины Е). Во-вторых, знать модули упругости необходимо не только
для того, чтобы рассчитывать деформации конструкции, но и для того, чтобы
деформации ее отдельных элементов были согласованными (тогда и напряжения
между этими элементами будут распределяться так, как мы хотели этого,
проектируя конструкцию).
Определяя модуль Юнга, мы
разделили напряжение на безразмерное число – деформацию, следовательно, модуль
имеет размерность напряжения. Если деформация равна 1 (100%), то напряжение
оказывается равным модулю упругости. Стало быть, модуль упругости можно
считать также напряжением, которое удваивает длину упругого образца. Легко
себе представить, что величина модуля упругости должна быть большой, обычно она
по крайней мере в 100 раз больше разрушающего напряжения: ведь материалы, как
правило, разрушаются, когда их упругая деформация превышает 1%.
Если взглянуть на величины
Е, то нетрудно понять, почему огромное количество твердых химических
соединений не может быть использовано в качестве конструкционных материалов. Мы
хотим, чтобы наши конструкции были как можно жестче, ведь колебания сооружений
(мостов, зданий, башен) и без того велики. Сталь – наиболее жесткий из
сравнительно дешевых материалов, и в этом одна из причин ее широкого
использования.
Увлечение Юнга
сопротивлением материалов не ограничилось открытием модуля упругости. Он изучал
кручение круглых стержней, изгиб консольных балок и дал много ценных
рекомендаций. Он первым заявил, что закон Гука действует только до
определенного предела, а затем упругая деформация не проявляется и становится
необратимой. Юнг не определил, как развивается зависимость между нагрузкой и
деформацией за пределами упругости, но он указал на существование этой области.
Наконец, Юнг занимался изучением сложнейшего вида деформации тел – разрушения
ударом. Так что это совсем неплохо для медика, увлекавшегося физикой и
философией. И все-таки самым значительным открытием Юнга остается модуль
упругости, без которого не обходится ни один инженерный расчет элемента,
конструкции, сооружения – от стола до железнодорожного моста, до космической
ракеты.
Следует четко усвоить, что
прочность и жесткость не одно и то же. Жесткость (модуль Юнга) показывает,
насколько податливым является материал. Прочность характеризуется напряжением,
необходимым для того, чтобы этот материал разрушить. Прежде всего существует
прочность на разрыв. Это напряжение, необходимое для того, чтобы разорвать
материал на части, разрушив все межатомные связи вдоль поверхности разрыва.
Стержень из очень прочной стали может выдержать растягивающее напряжение до 300
кгс/мм2. А вот обычный кирпич выдержит лишь 0,4-0,6 кгс/мм2.
Следовательно, прочность материалов, используемых в механике, может изменяться
примерно в тысячу раз.
Говоря о прочности, имеют в
виду прочность на разрыв, хотя материалы чаще работают на сжатие, чем на
растяжение. Казалось бы, если мы пытаемся прижать атомы один к другому, это не
должно вызывать разрушения. Однако разрушения происходят, хотя представляют
собой явления более сложные, чем разрыв. Под действием сжимающей нагрузки
материал может ломаться самым различным образом.
Как работает конструкция на
растяжение и сжатие, понять довольно легко, но как те же самые растяжение и
сжатие позволяют балкам выдерживать нагрузки – это далеко не очевидно. А между
тем разного рода балки составляют значительную долю всех конструкций, с
которыми мы повседневно сталкиваемся. Самая обычная половая доска, которая чуть изгибаясь, выдерживает значительный вес мебели
и людей – наглядный пример балки. История расчета изгибаемой балки – одного из
наиболее распространенных элементов в технике – является наглядным примером
попыток перейти от общих умозрительных рассуждений к решению практических
задач.
Расчет балки на прочность
при изгибе был сделан Кулоном в его знаменитом труде "О применении правил
максимума и минимума к некоторым вопросам статики, имеющим отношение и
архитектуре". Знаменитый французский ученый Шарль Огюстэн
Кулон (1736-1806) широко известен прежде всего как создатель основного закона
электростатики, выражающего зависимость силы взаимодействия двух неподвижных
точечных электрических зарядов от расстояния между ними. Имя Кулона носит не
только этот закон, но и единица электрического заряда. Но Кулон и в
строительную механику внес такой вклад, которого было бы достаточно для того,
чтобы обеспечить ему бессмертие, даже если бы он не открыл закон
электростатики. Имея большой инженерный опыт и талант исследователя, Кулон
после долгих лет практической работы по строительству различных сооружений
написал научную работу, содержавшую, кроме расчета изгибаемой балки, методы
расчета подпорных стен и сводов. Созданные Кулоном более двухсот лет назад,
эти методы применяются в практике проектирования до сих пор почти без
изменения. Кулон построил собственную стройную теорию сводов, которая заняла
достойное место в строительной механике. Кулон занимался изучением сложного
вида деформации – кручения. Его формулы по кручению для стержней малого диаметра
также применяются до сих пор. Наконец, Кулон, изучив разрушение сжатых
элементов, приходит к выводу, что главной причиной разрушения является сдвиг.
Такое предположение стало основой для утверждения нового взгляда, названного
впоследствии третьей теорией прочности.
Блестящие работы Галилея, Гука, Мариотта,
Кулона, других ученых ХVII - ХVIII вв. подготовили почву для возникновения
инженерной науки. Особенно бурно она развивается во Франции. На первое место из
всех отраслей техники вырывается военная. Поэтому инженерное дело в своей
основе было прежде всего делом военных специалистов. Основные технические
термины также имеют "военное" происхождение. Так, слово
"машина" вначале употреблялось в значении орудие, снаряд, военное
приспособление, а слово "инженер" означало изобретатель пушек. В 1729
г. для учебных заведений по подготовке специалистов фортификационных и других
военных сооружений французский ученый Белидор издал
учебник "Инженерная наука". Это был первый в мире учебник по
инженерному делу, посвященный строительству и архитектуре. Он переиздавался в
течение 102 лет! Последнее издание вышло в 1830 г. почти без изменений. Такую
невиданную популярностъ можно объяснить фундаментальностью
построения, а также широким охватом как теоретических, так и практических
вопросов строительства. Содержал учебник и сведения по сопротивлению материалов.
Белидор приводит расчеты сводов, подпорных стен,
балок, таблицы прочности материалов, применяющихся в строительстве. В 1798 г.
инженером мостов и дорог Жираром издается первый
учебник по сопротивлению материалов – "Аналитический трактат о
сопротивлении твердых тел". В 1794 г. в Париже открывается знаменитая
Политехническая школа, основоположником которой является знаменитый математик
Гаспар Монж (1746 - 1818). Первыми педагогами в ней были крупнейшие французские
ученые – Лагранж, Монж, Пуассон и другие. Надо сказать, что правительство
Наполеона Бонапарта поощряло развитие науки и техники. Сам Наполеон, по
свидетельству современников, серьезно увлекался математикой и обладал большими
способностями в этой области.
Первое потрясение основ галилеевской науки о прочности связывают с именем
знаменитого французского инженера и ученого Луи Мари Анри Навье (1785-1836).
Получив образование в Школе мостов и дорог, он начал работать
инженером-строителем. Очень скоро обнаруживаются большие теоретические
способности молодого инженера, его талант исследователя-теоретика. Навье
публикует ряд своих разработок, которые обобщает затем в курсе лекций,
созданном в 1826 г. К этому времени он был уже академиком. Книга Навье стала
важной вехой в истории строительной механики. Было положено начало теории
упругости. Вместо принципа расчета по предельному, разрушающему состоянию
материала утверждался принцип рабочего состояния.
Область нагрузок, где закон
Гука действует безукоризненно, называют упругой стадией работы материала. Затем
при возрастании нагрузки в материале начинается пластическая деформация,
пропорциональность между силой и деформацией исчезает, возникают более сложные
явления, которые в XIX в. невозможно было описать математически. В основу
новой теории Навье – теории упругости – было положено полное принятие закона
Гука. Навье вводит понятие напряжения, т.е. силы, действующей на единицу
площади сечения элемента, к которому эта сила приложена. Напряжение – это,
таким образом, удельное давление (кгс/см2). Если на колонну размером
20х20 см нагружено, например, 40 т груза, то это значит, что напряжение сжатия
в колонне составит 100 кгс/см2. Навье предлагал установить расчетные
допускаемые напряжения, при которых конструкция может работать надежно, и на
эти напряжения вести расчет. Естественно, допускаемые напряжения должны быть
значительно меньше разрушающих. Если стальная балка разрушается при напряжении
4000 кгс/см2, то Навье предлагает при изгибе принимать допустимое
напряжение равным 1300 кгс/см2. Размеры балки при расчете принимают
такими, чтобы во время эксплуатации она имела напряжение не выше допустимого.
Расчет по допускаемым напряжениям господствовал в строительной механике более
века, а в некоторых сооружениях применяется до сих пор.
Уравнения равновесия
твердого тела, выведенные Навье, это уравнения равновесия между внешними
силами, действующими на тело, и внутренними силами между частицами этого тела.
Навье считал, что на любое сечение при деформации действует система
молекулярных сил, каждая из которых действует на бесконечно малую площадку.
Для того чтобы элемент работал нормально, эта система сил должна находиться в
равновесии.
Теорию упругости Навье
развил французский ученый Огюстен Луи Коши (1789 - 1857). Если Навье выводил
свои уравнения равновесия из представлений о молекулярной структуре и силах
межатомного взаимодействия, то Коши использовал более очевидное представление
о давлении воды на плоскость. Коши принадлежит гипотеза о том, что давление
на любую поверхность твердого тела не обязательно должно быть перпендикулярным.
А затем он уже выводит те уравнения, с которых в современных высших учебных
заведениях во всем мире начинается изучение теории упругости.
Коши изучает маленький
кусочек вещества, вырезанный из любого участка твердого тала, например, изгибаемой
балки. Поскольку вырезанный кусочек в теле был связан со всех сторон силами, то
при обрыве этих связей он должен изменить форму и размеры. Чтобы этого не
произошло, т.е. чтобы сохранилось равновесие, мы должны ко всем граням этого
тела приложить такие силы, которые бы в точности восстановили его прежнюю
форму в теле так, как будто разрезов и не было. Приведя в порядок силы на
гранях элементарного объема, т.е. разлагая их на нормальные, перпендикулярные,
и сдвигающие, действующие в плоскости грани, можно получить уравнения,
связывающие напряжения на разных гранях друг с другом. Изучая напряженное
состояние элементарного кусочка балки математическими методами, Коши открыл
законы, по которым сила передается с одних граней на другие. Это очень важный
момент в познании законов, по которым можно определить сжатые и растянутые,
перегруженные и ненагруженные места в элементе. Для описания поведения тела
Коши вводит много новых терминов, отражающих определенные явления. Им
устанавливается точное число разного вида напряжений, которое необходимо для
полной характеристики механического состояния любой напряженной внутри тела
плоской поверхности. Коши показывает, что в теле всегда можно выделить такие
площади, в которых будут действовать только нормальные, т.е. перпендикулярные к
сечению силы – он их назвал главными напряжениями, а их направления – главными
направлениями. Соответственно деформации, которые вызваны главными
напряжениями, названы им главными деформациями. В конечном счете Коши выводит
полную систему из трех уравнений для решения задач теории упругости.
Немногим позже уравнениями
равновесия занялся современник Навье и Коши, их соотечественник Пуассон (1781 -
1840). Он доказал, что эти три уравнения не только необходимы, но и достаточны
для того, чтобы рассчитывать напряженное состояние твердого тела. Симеон Дени
Пуассон главным образом занимался физикой и решил много сложнейших задач. В
механике же, кроме уравнений равновесия, колебаний и прогиба стержней, изгиба
круглых пластинок и других задач, Пуассон оставил память о себе тем, что ввел
коэффициент, получивший его имя. Еще Юнг отметил, что при сжатии стержня
поперечное сечение элемента увеличивается, а при растяжении – уменьшается. Так
вот, отношение упругого уменьшения или увеличения поперечного размера элемента
к его продольному удлинению или укорочению является величиной, постоянной для
каждого материала. Пуассон исходил из того, что объем элемента до приложения
нагрузки и после этого не изменяется. Изменяется лишь форма. В частности, при
сжатии стержня увеличивается его площадь сечения и уменьшается высота. При
растяжении, наоборот, уменьшается площадь сечения и увеличивается высота. При
таком подходе влияние материала не учитывалось, считалось, что он не играет
роли. Поэтому коэффициент Пуассона был величиной постоянной для любого
материала, равной 0,25. В дальнейшем величина и универсальность коэффициента
Пуассона подверглись сомнению. Английский исследователь Джордж Грин, решая
уравнения теории упругости из условия сохранения энергии, теоретически приходит
к тому, что коэффициент Пуассона не может быть постоянной величиной для всех
материалов. Опыты показали, что коэффициент Пуассона, как и модуль Юнга,
отражает особенности атомных взаимодействий. Объем деформированного тела, как оказалось,
может изменяться за счет перераспределения атомных связей в пространственной
структуре вещества. Поэтому для некоторых материалов коэффициент Пуассона
может быть даже близок к нулю. Например, для металла бериллия измерения дают
величину 0,03, для алмаза – 0,07. Значит, эти материалы, растягиваясь в длину,
почти не сокращают межатомных расстояний в поперечном направлении, настолько
эти связи жестки при сближении. Теперь существует таблица значений коэффициента
Пуассона для различных материалов. Важная константа Пуассона вошла во все
уравнения теории упругости, и без нее не обходится ни один инженерный расчет.
После исследований Навье,
Коши и Пуассона главные уравнения теории упругости стали классическими, чуть ли
не идеальными. Однако незыблемость принятых теорий прочности во второй половине
XIX в. значительно пошатнулась. И связано это было опять-таки с развитием
техники, которая задавала науке все более сложные задачи. Накопив довольно
обширный материал по растяжению и сжатию, теория упругости еще плохо
справлялась с таким видом деформации, как кручение. В этой области значительные
результаты получил французский ученый Адемар Жан Клод
Барре Сен-Венан (1797-1886), которому было суждено оставить заметный след в
истории теории упругости. Сен-Венаном написано огромное число работ в самых
различных областях механики твердого тела. Ему, кстати, принадлежит
оригинальный способ публикации своих идей. Так, он издает курс лекций глубоко
почитаемого им Навье со своими примечаниями в виде книги (в 1864 г.), в которой
1/10 места была занята лекциями, а 9/10 – примечаниями к ней. Но наибольшую
известность получили два его мемуара (о кручении и об изгибе призм), не утратившие
своего значения до наших дней. В советском издании 1961 г. они заняли объем в
500 страниц! Сен-Венан разрабатывает теорию пластичности для двумерных задач.
Им найдена весьма важная область распространения напряжений – зона действия
внешних сил, и открыт принцип, получивший его имя.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов