Главная
Тема 2. Растяжение-сжатие
прямого стержня
Во введении в сопротивление материалов приводятся определения основных понятий курса: напряжения и деформации. Они были установлены в механике деформируемого твердого тела О.Коши в мемуаре, представленном в Парижскую академию наук в 1822 г., краткое содержание которого в виде статьи [339] было опубликовано в 1823г. Современное определение понятия напряжения было дано Б.Сен-Венаном в 1845г. [88].
Работа О.Коши была подготовлена исследованиями Л.Навье который в мемуаре, представленном в Парижскую академию наук в 1821г. и опубликованном в 1827г. [448] (а в сокращенном виде в 1823г. [445], развил молекулярную теорию упругого твердого тел и вывел уравнения его равновесия и движения в перемещениях. Вероятно, эта работа и побудила О.Коши написать вышеупомянутый мемуар, так как он был назначен Парижской академией наук членом комиссии по рассмотрению мамуара Л.Навье. Представление о том, что свойство упругости может быть объяснено силами притяжения и отталкивания, действующими между мельчайшими частицами тел, существовало еще со времен И.Ньютона, и было предметом исследования Р.Бошковича, рассмотренным в его книге [327], опубликованной в 1763г.
При постановке задачи растяжения стержня обычно формулируется принцип Б.Сен-Венана. Согласно этому принципу применительно к стержням особенности приложения внешних сил к растянутому или сжатому стержню проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Этот принцип был высказан Б.Сен-Венаном в 1853г. в мемуаре [255] и обоснован им опытами. На общий случай деформируемого тела этот принцип был распространен учеником Б.Сен-Венана механиком Жозефом Валентином Буссинеском (Boussinesg J.V. 13.03.1842 — 19.02.1929) в 1885г. [328]. В статье [38] рассмотрены работы, в которых дано доказательство принципа. В.З.Власовым показано в 1940г. [143], что этот принцип несправедлив для тонкостенных стержней.
При определении удлинения растянутого стержня используется закон, открытый Р.Гуком, устанавливающий пропорциональность напряжения деформации. Впрочем, понятия напряжения и деформации не были известны Р.Гуку. Как было указано выше, они были введены в механику деформируемого твердого тела значительно позже в 1822 г. 0. Коши.
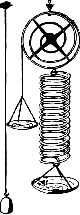
Испытания пружин и стальной проволоки, выполненные Р.Гуком
Работая над созданием конструкции регулятора точного хода часов, Гук производил испытания плоских спиральных пружин и установил, что угол закручивания пружины пропорционален приложенному моменту. Затем он повторил опыты на растянутой витой пружине, растянутой стальной проволоке, консольной деревянной балке, изогнутой силой, приложенной на свободном конце. На рисунке приведены, взятые из работы Р.Гука [389] иллюстрации трех испытаний пружин и стальной проволоки. В ходе этих исследований он установил, что во всех случаях перемещения прямо пропорциональны приложенным силам. Таким образом, закон Гука был получен экспериментально для следующих типов нагружения: растяжение (стальная проволока), кручение (витая пружина), изгиб (спиральная пружина и деревянная балка). Этот закон был открыт в 1660г., однако Р.Гук опубликовал его только в 1676г., в конце одной катлеровской лекции [388] в виде анаграммы ceiiinosssttu, которая представляет собранные в алфавитном порядке буквы латинской фразы: ut tensio sic vis, что в переводе означает: какова сила, таково и действие, т.е. результат силы (в данном случае перемещение). Указанная анаграмма была раскрыта Р.Гуком в 1678г. в другой катлеровской лекции [389] Гук производил испытания при не очень больших нагрузках, предполагая, по-видимому, что его закон справедлив всегда.
Независимо от Р.Гука закон прямой пропорциональности перемещений приложенным силам был установлен Э.Мариоттом в результате испытаний деревянных и стеклянных стержней на растяжение и изгиб (консольный стержень, нагруженный силой на конце). Эти опыты описаны в его книге [426], вышедшей в свет в 1686г. и посвященной в основном движению жидкостей.
Ограниченность закона Гука, т.е. справедливость его только в начальной стадии нагружения, установил Т.Юнг который также определил понятие модуля упругости, хотя и в форме, отличной от принятой в настоящее время. Т.Юнг ввел две величины: вес модуля EA, где A площадь поперечного сечения стержня, и высоту модуля
![]()
где ρ — плотность тела. Первая величина не является постоянной материала. Это жесткость стержня при растяжении. Вторая — постоянная материала, имеющая размерность длины. Определение модуля упругости дано Юнгом в такой весьма туманной форме: «Модуль упругости какого-либо вещества представляет собой столбик этого вещества, способный произвести давление на свое основание, которое так же относится к весу, создающему некоторую степень сжатия, как длина столбика к уменьшению его длины».
Т.Юнг обратил внимание на то, что при
растяжении — сжатии поперечные размеры стержня изменяются. Эти положения
сформулированы им в двухтомном курсе лекций, изданно
в 1807г. [506], которые Т.Юнг читал в Королевском институте. Механик и историк
механики Клифорд Эмброуз Трусделл (TruesdellC.E.)
указывает [117], что в манускрипте Л.Эйлера, написанном в 1727 г. (за 80 лет до выхода в свет
книги Т.Юнга), но опубликованном только в 1862 г., содержится понятие модуля
упругости E, хотя для его использования в дальнейшем он применял
величину
![]()
т.е. высоту модуля по Юнгу [6].
Математик, механик и архитектор Джордано Риккати (RiccatiG., 25.02.1709 — 20.07.1790) по экспериментально измеренной частоте изгибных колебаний стальных и латунных цилиндров в 1767г. определил отношение их модулей упругости [473], т.е.провел первое экспериментальное исследование модулей упругости.
По-видимому, Д.Риккати использовал понятие модуля упругости, которое, как указано выше, было опубликовано только в 1862г.
Абсолютная величина отношения поперечной деформации к продольной, постоянная в пределах справедливости закона Гука, связана с именем С.Пуассона который ввел ее в своем мемуаре, представленном в Парижскую академию наук в 1829г. [462], и на основе молекулярной теории установил, что она равна 1/4.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов