Главная
Тема 15. Пластины
и оболочки
В курсе сопротивления материалов в лучшем случае удается изложить теорию изгиба только круглых осесимметрично нагруженных пластин.
Вероятно, первой работой, в которой была сделана попытка исследования деформирования мембран, была работа Л.Эйлера [361] опубликованная в 1767г. и посвященная колебаниям гибкой мембраны. Последняя в этой работе рассматривалась как система струн натянутых в двух взаимно перпендикулярных направлениях. В такой постановке Л.Эйлер вывел дифференциальное уравнение для прогиба. Такой же подход имел место в работе Якова Бернулли младшего [325], относящейся к 1789 г., который получил дифференциальное уравнение изгиба пластины. Однако он сам понимал, что его решение является весьма приближенным.
Особенный интерес к задаче
изгиба пластин возник в связи с публикацией в 1802 г. книги физика Эрнста Флоренса Фридриха Хладни (ChladniE.F. F, 30.11.1756 — 03.04.1827)
по акустике [342] и с его докладом в Парижской академии наук в 1809г., в
котором он экспериментально продемонстрировал существование узловых линий при
колебаниях пластинок. Эти эксперименты произвели большое впечатление на
присутствовавшего на заседании Наполеона. По его предложению Парижская академия
наук назначила премию за создание математической теории колебаний пластин.
Единственной работой, поданной на конкурс в октябре 1811 г., была работа С.Жермен.
Она, следуя работе Л.Эйлера по изгибу балок, попыталась
получить дифференциальное уравнение изгиба пластины из выражения энергии
деформации. Величину ее она записывала в виде
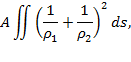
где ρ1 и ρ2 — главные радиусы кривизны изогнутой поверхности, т.е. такая запись неверна. Причем при вычислении вариации интеграла, определяющего потенциальную энергию деформации, допустила ошибку. Поэтому работа не получила премии. Ж.Лагранж, который был членом жюри, исправил ошибку и получил правильное дифференциальное уравнение изгиба пластины. Конкурс был объявлен вторично с новым сроком в октябре 1813 г. Несмотря на то, что, на этот раз результат решения был верен, академия не присудила ей премию, так как сочла исходное уравнение для потенциальной энергии деформации пластины необоснованным. Конкурс был объявлен в третий раз, и в 1816 г. третья попытка С.Жермен увенчалась успехом, хотя жюри считало, что и в этот раз в работе нет достаточно мотивированного обоснования исходного уравнения. Работы С.Жермен опубликованы в 1821и 1826гг. в двух мемуарах [367, 368].
В 1828 г. О.Коши [340] и С.Пуассон в 1829 г. [462] подошли к решению задачи изгиба пластины, используя основные уравнения теории упругости. Они разлагали все напряжения и перемещения в ряд по степеням расстояния точек от средней плоскости пластины. Из этих решений при минимально возможном числе членов ряда может быть получено решение С.Жермен. При большем числе членов можно получать более точные решения и, в частности, для толстых пластин.
Вокруг этих работ возникла полемика. Б.Сен-Венан [344] считал, что использованные ряды должны расходиться. (Заметим, что область сходимости этих рядов до сих пор не выяснена.) Возникли также споры относительно числа граничных условий.
Заметим, впрочем, что еще Л Навье [446] в 1823 г. вывел дифференциальное уравнение равновесия пластины, принимая, что составляющие перемещения, параллельные ее срединной плоскости, пропорциональны расстоянию от нее. Это уравнение использовано для решения задачи изгиба прямоугольной пластины, нагруженной равномерно распределенной нагрузкой или сосредоточенной силой, приложенной в центре пластины. Для решения задачи сформулированы граничные условия. Решение получено в виде двойного тригонометрического ряда.
Г.Кирхгоф разработал в 1850 г. [403] теорию изгиба пластин на основе двух гипотез: 1) нормальными напряжениями в площадках, параллельных срединной плоскости, можно пренебречь; 2) точки, лежащие на прямой, перпендикулярной срединной плоскости, после деформации снова образуют прямую, нормальную к деформированной поверхности. Сформулированные гипотезы являются аналогами соответствующих гипотез теории изгиба балок. Эта теория сразу завоевала признание и используется в настоящее время. Понятие о внутренних силах, передающихся через единицу длины сечения, было впервые введено механиком Ф.Герингом в 1860 г. [З66], а затем развито Г.Кирхгофом в 1876 г. [406]. А.Клебш в 1862 г. [344] впервые составил уравнения равновесия элемента пластины, в которые вошли эти внутренние силы. Им же впервые была решена задача об осесимметричном изгибе круглой пластины.
Расчету элементов конструкций корабля в форме пластин различных очертаний посвящен третий том монографии механика и инженера П.Ф.Папковича [227], опубликованный в 1941 г.
Теория оболочек, основанная на гипотезах Г.Кирхгофа, была разработана механиком X.Ароном (AronH.) [313] в 1874 г. Однако в этой работе допущены некоторые неточности, которые были замечены и исправлены в 1888 г. математиком и механиком Агастесом Эдуардом Хьютом Лявом (LoveA.E. H., 17.04.1863 — 05.06.1940) [423, 66].
Большой вклад в теорию оболочек внесли В.Л.Бидерман и др. В работах А.И.Лурье [205] уравнения теории оболочек выведены из общих уравнений теории упругости. В статье В.В.Новожилова и P.M.Финкельштейна [218], опубликованной в 1943г., показано, что погрешность допущений Кирхгофа в теории тонких оболочек имеет величину порядка h/R (где h — толщина, R — радиус кривизны срединной поверхности). В книге [219], опубликованной в 1952 г., установлена возможность представления уравнений теории оболочек в комплексной форме, что открывает новые пути преобразования уравнений и их решения.
В работах А.Л.Гольденвейзера [155] сформулированы условия неразрывности деформаций и показана возможность тождественного удовлетворения уравнений равновесия путем введения четырех функций напряжений.
В курсе сопротивления материалов в лучшем случае удается рассмотреть краевой эффект при осесимметричном изгибе цилиндрической оболочки. Однако безмоментная теория осесимметрично нагруженных оболочек вращения обычно всегда излагается. В этом случае напряжения определяются из двух уравнений равновесия, одно из которых представляет собой уравнение равновесия части оболочки, отсеченной конической поверхностью, а второе — уравнение равновесия элемента оболочки, вырезанного двумя коническими и двумя меридиональными сечениями, называемое уравнением Лапласа, получившего его при разработке теории капиллярности.
Исследование
прочности цилиндрических оболочек, проведенное Э.Мариоттом
А.С.Григорьев вывел основные уравнения деформирования безмоментных оболочек вращения
при больших деформациях и перемещениях за пределами пропорциональности и на
основе их решил ряд задач [156, 157]. По-видимому, первое экспериментальное
исследование прочности цилиндрических оболочек, нагруженных давлением жидкости,
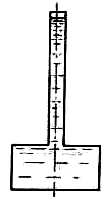
произвел Э.Мариотт [426]. Он наполнял водой тонкостенный
цилиндрический резервуар с укрепленной на нем длинной цилиндрической трубой.
Увеличивая высоту уровня воды в трубе, он добивался разрушения резервуара. В
результате Э.Мариотт установил, что прочность резервуара прямо пропорциональна
толщине стенки и обратно пропорциональна диаметру и что трещина в резервуаре
возникает в меридиональном направлении.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов