Главная

Лекция 4 (продолжение). Задачи для самостоятельного решения

Содержание

Геометрические характеристики простых сечений

Геометрические характеристики сложных сечений

Геометрические характеристики простых сечений

Задача 1.

Относительно какой из множества параллельных осей осевой момент инерции принимает наименьшее значение?

Задача 2.

Относительно какой из множества параллельных осей в пределах площади равностороннего треугольника осевой момент инерции принимает наибольшее значение?

Задача 3.

Какой из двух моментов инерции квадратного сечения больше: относительно центральной оси, параллельной сторонам или относительно оси, совпадающей с диагональю?

Задача 4.

В каких случаях можно без вычислений установить положение главных осей инерции фигуры?

Задача 5.

Не прибегая к интегрированию, найдите центробежный момент инерции прямоугольного треугольника относительно центральных осей, параллельных катетам.

Задача 6.

Докажите, что если для данной плоской фигуры главные моменты инерции равны между собой, то любая ось, проходящая через начало координат, является главной.

Задача 7.

Для произвольной плоской фигуры найдите геометрическое место точек, относительно которых сечение имеет одинаковую величину полярных моментов инерции.

Задача 8.

Для плоской фигуры найдите точку, обладающую тем свойством, что все проходящие через нее оси являются главными.

Задача 9.

Для прямоугольника высотой h и шириной в определить, во сколько раз увеличатся момент инерции и момент сопротивления относительно центральной оси x, если увеличить вдвое:

1) высоту h или

2) ширину в.

Ответ: увеличатся: 1) J _x в восемь раз, W_x – в четыре; 2) J _x и W_x – вдвое.

Задача 10.

Составить выражения для осевых и центробежных моментов инерции прямоугольника со сторонами в и h относительно центральных осей x и y, повернутых на угол 30⁰ к главным осям. Какой вид примут полученные выражения для квадратного сечения со стороной а ?

Ответ: для квадрата

Задача 11.

Определить осевые моменты инерции прямоугольника высотой h и шириной b относительно осей х и у, являющихся его осями симметрии (см. рис.).

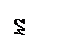
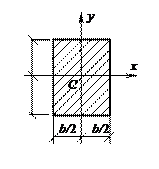
Ответ: I_x = bh³/12; I_y = hb³/12.

Задача 12.

Определить статический момент S_x поперечного сечения в виде равнобокой трапеции (см. рис.). Найти положение центра тяжести С. Вычислить главные моменты инерции относительно главных осей х_с, у. Можно ли применить полученные результаты для вычисления соответствующих геометрических характеристик поперечных сечений в виде равнобедренного треугольника и прямоугольника?

Ответ:

Задача 13.

Покажите, что для прямоугольного сечения с отношением сторон h/b=2 любые оси, проведенные через середину одной из длинных сторон, являются главными.

Задача 14.

Определите указанные ниже величины.

Задача 15.

Как изменится момент инерции и момент сопротивления квадрата со стороной а относительно оси х, если сечение повернуть на угол 45⁰, оставив ось х горизонтальной.

Ответ: момент инерции не изменится; момент сопротивления уменьшится на 41%

Задача 16.

Сравнить величины моментов инерции относительно центральной оси х сечений прямоугольника, квадрата и круга при условии, что площади F всех трех сечений одинаковы.

Ответ: а) I_х=0,167F²; б) I_х=0,0833F²; в) I_х=0,0797F²

Задача 17.

Для прямоугольника со сторонами в=2 см и h=3 см определить положение главных осей, проходящих через точку О, и вычислить главные моменты инерции.

Ответ:

Задача 18.

Найти моменты инерции полукруга относительно главных центральных осей инерции (см. рис.).

Ответ:

Задача 19.

Определить статические моменты плоского прямоугольного сечения относительно осей х и у (рис. 1).

Определить координаты центра тяжести плоского сечения в форме половины круга радиусом R (рис. 2).

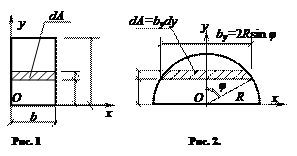
Ответ к рис. 1: S_x = bh²/2; S_y = hb²/2.

Задача 20.

Определить координаты центра тяжести плоского сечения, ограниченного осью х, квадратной параболой x = hy²/b² и прямой линией х = h (рис. 1).

Определить координаты центра тяжести плоского сечения, ограниченного осью х, кубической параболой x = hy³/b³ и прямой линией x = h (рис. 2).

Определить координаты центра тяжести плоского сечения, ограниченного осью у, кубической параболой x = hy³/b³ и прямой линией у = в (рис. 2).

Решение к рис.1. Для нахождения центра тяжести воспользуемся формулами В первую очередь по формуле определяем площадь поперечного сечения

Затем по формулам находим статические моменты сечения:

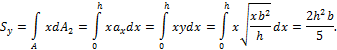
И, окончательно, по формулам определяем

Ответ к рис 1: x_1c = 0,375b; y_1c = 0,6h.

Ответ к рис 2: x_1c = 4h/7; y_1c = 0,4b.

Ответ к рис.3: x_2c = 2h/7; y_2c = 0,8b.

Геометрические характеристики сложных сечений

Задача 1.

Сравнить моменты инерции относительно горизонтальной оси х двух равновеликих прямоугольных сечений, ослабленных вырезами одинаковой площади.

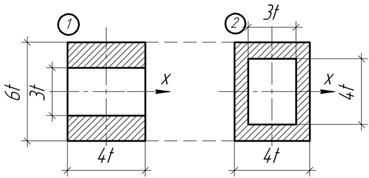
Ответ:

Задача 2.

Определить положения центра тяжести сечения и его моменты инерции I_x и I_y относительно центральных осей. а=10 см.

Задача 3.

Сравнить моменты сопротивления W_х двух равновеликих прямоугольных сечений, ослабленных вырезами одинаковой площади F=2а²

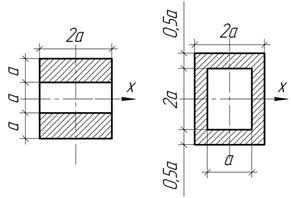
Ответ:

Задача 4.

Плоская фигура состоит из полукруга и квадрата со стороной а=10 см. Определить разность моментов инерции относительно главных осей, проходящих через точку О.

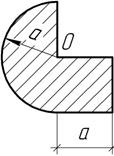
Ответ:

Задача 5.

Определить положение центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10см.

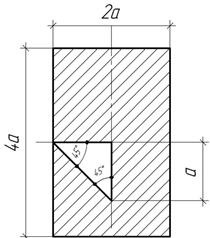
Задача 6.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 7.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

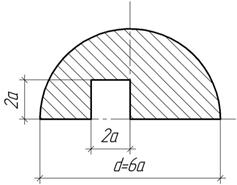
Задача 8.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 9.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 10.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 11.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 12.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 13.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

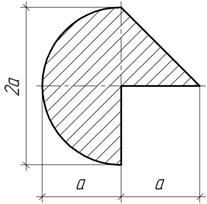
Задача 14.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 15.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 16.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 17.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 18.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

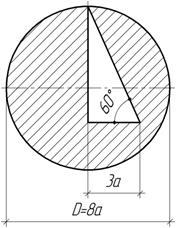
Задача 19.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 20.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

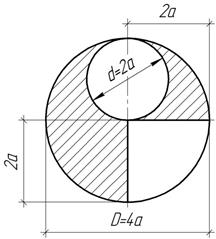
Задача 21.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

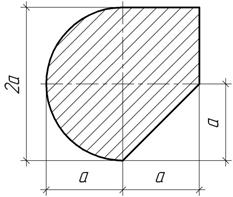
Задача 22.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

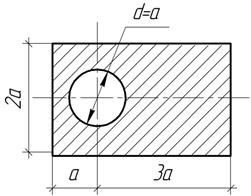
Задача 23.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 24.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

Задача 25.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

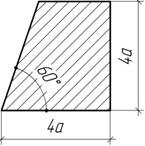
Задача 26.

Определить положения центра тяжести сечения и его моменты инерции I_х и I_у относительно центральных осей при а=10 см.

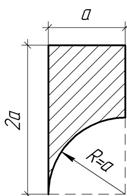
Задача 27.

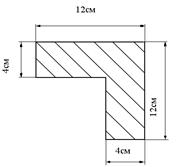
Определить центр тяжести поперечного сечения, показанного на рисунке.

Указания. Для определения положения центра тяжести сложного сечения рекомендуется следующий порядок действий:

1. Сложное сечение разбивается на части, имеющие вид простых фигур.

2. Определяются площади и положения центров тяжести каждой простой фигуры.

3. Выбираются случайные (произвольные) координатные оси х и у. Случайные оси желательно выбирать так, чтобы все точки плоского поперечного сечения имели положительные координаты.

4. По формулам

которые можно записать как

вычисляются статические моменты S_x и S_y всего плоского сечения как суммы статических моментов S_xi, S_yi каждой фигуры относительно осей x, y.

5. По формулам вычисляются координаты центра тяжести всего сечения.

Ответ: х_с = 5а/6; у_с = 5а/6 (Центр тяжести С должен лежать на оси симметрии поперечного сечения).

Задача 28.

Определить величины главных центральных осевых моментов инерции составного сечения.

Задача 29.

Определить статические моменты S_x, S_y сложного поперечного сечения (см. рис.) и найти координаты его центра тяжести.

Указание. Рассматриваемое сложное сечение разбить на три прямоугольника.

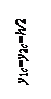
Ответ: S_x = 7h³/64, S_y = 19h³/512; x_c = 19h/112; y_c = h/2.

Задача 30.

Определить осевые моменты инерции I_x, I_y для квадратного поперечного сечения (рис. 1).

Определить осевые моменты инерции I_x, I_y для поперечного сечения, показанного на рис. 2.

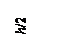
Ответ к рис.1: I_x = I_y= a⁴/12.

Ответ к рис.2: I_x = (bh³ – b₁h₁³)/12; I_y = (hb³ – h₁b₁³)/12.

Задача 31.

Определить осевые моменты инерции и центробежный момент инерции относительно центральных осей х_с, у_с для сечения, изображенного на рисунке. Вычислить значения главных моментов инерции и определить расположение главных осей инерции. Центр тяжести поперечного сечения находится в точке С.

Ответ:

Задача 32.

Определить главные моменты инерции относительно главных осей х, у для плоского поперечного сечения, показанного на рисунке. Для вычислений принять h = 12 см, b = 8 см, t = 1 см.

Ответ: I_x = 2313,3 см⁴; I_y = 697,3 см⁴.

Задача 33.

Определить момент инерции относительно центральной оси y сечения, изображенного на рисунке. Размеры показаны в мм.

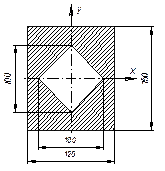
Ответ: J_х =3167 см⁴.

Задача 34.

Как изменятся площадь и момент инерции J_у сечения трубчатой балки, изображенной на рис. а), если заменить одно отверстие диаметром 200 мм—двумя, диаметром каждое по 100 мм, расположенными, как показано на рис. б)?

Ответ: Площадь увеличится на 38,6%, а момент инерции уменьшится на 2%.

Задача 35.

Определить координату у_С центра тяжести несимметричного двутавра (см. рис.).

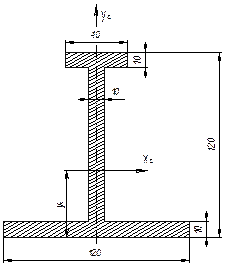
Ответ. Координата у_c = 43,1 мм.

Задача 36.

Определить моменты инерции относительно центральных осей х_С и у_С сечения передней оси автомобиля, которое показано на рис.

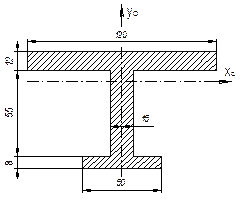
Ответ. Моменты инерции: J_xс =198 см⁴; J_yс =183 см⁴.

Задача 37.

Сечение балки состоит из двух швеллеров № 33b, усиленных двумя листами 14х300 мм, приклепанных к полкам. Определить момент инерции сечения относительно центральной оси у с учетом ослабления его заклепочными отверстиями d = 23 мм (см. рисунок) и оценить ослабление сечения (в процентах к моменту инерции неослабленного сечения).

Ответ: J_х =35200 см⁴; ∆J=16,5%.

Задача 38.

Поперечное сечение раскоса навесного плуга изготовлено из двух равнополочных уголков размером 63х63х5 (см. рис.). Определить моменты инерции относительно центральных осей х_С и у_С.

Ответ. Моменты инерции: Jx_С = Jy_С = 70,5 см⁴.

Задача 39.

Поперечное сечение стержня (см. рис.) состоит из двутавра № 55 (ГОСТ 8239-72), швеллера № 18 (ГОСТ 8240-72). Определить расстояние х_С от центра тяжести двутавра с₁ до центра тяжести с всего сечения.

Ответ. Искомое расстояние х_С = 44 мм.

Задача 40.

На рис. показано сечение поперечины прицепного устройства пропашного трактора. Определить моменты инерции сечения относительно центральных осей х_С и у_С.

Ответ. Моменты инерции: Jx_С = 14,7 см⁴; Jy_С = 119,6 см⁴.

Задача 41.

Определить моменты инерции относительно центральных осей х_С и у_С сечения кронштейна растяжек пропашного трактора (см. рис.).

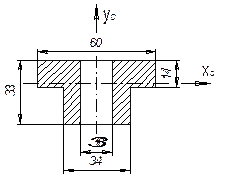
Ответ. Моменты инерции: Jx_С = 8,0 см⁴; Jy_С =30,3 см⁴.

Задача 42.

Определить моменты инерции относительно центральных осей х_С и у_С двух различных сечений рамы трактора, показанных на рис. а, б.

Ответ. Моменты инерции (в табл.).

Сечение	а	б
JхС, см^4	324	1604
JуС, см^4	932	9271

Задача 43.

Определить моменты инерции относительно центральных осей х_С и у_С сечения опорной поперечины рамы тракторного прицепа (см. рис.).

Ответ. Моменты инерции: J_хс,= 830 см⁴; J_ус = 527 см⁴.

Задача 44.

Докажите, что для фигуры, составленной из квадрата и равностороннего треугольника, прямая, соединяющая их центры тяжести, является главной осью, независимо от взаимного расположения квадрата и треугольника.

Задача 45.

Где на прямой ou надо выбрать начало системы координат, для которой эта ось была бы главной?

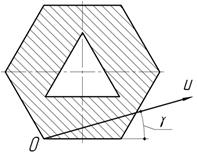
Задача 46.

Доказать, что для фигуры, составленных из двух одинаковых прямоугольников площадью А, прямая, соединяющая их центры тяжести, является главной осью, а величины главных моментов инерции принимают значения:

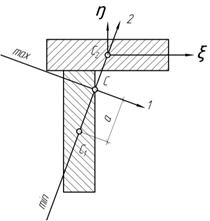
Задача 47.

Определить положение главных центральных осей тонкостенного сечения. Толщина стенки постоянна, мала и равна t. Размеры даны по средней линии сечения.

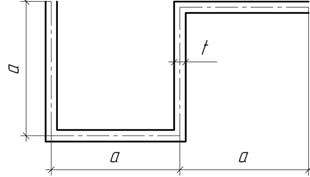
Задача 48.

Для сечения в виде ромба определить, при каких соотношениях между размерами b и h будут наибольшими момент инерции и момент сопротивления относительно горизонтальной оси х. Сторона ромба постоянна и равно а.

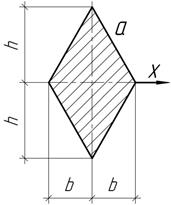
Задача 49.

При каких соотношениях между высотой h и основанием b прямоугольника, вписанного в круг, момент инерции и момент сопротивления относительно горизонтальной оси х будет максимальным?

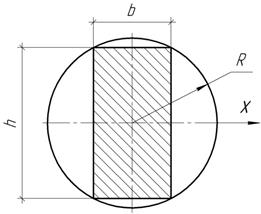
Задача 50.

При каких значениях h все оси, проходящие через точку О трапеции, будут главными?

Задача 51.

При каком соотношении между размерами а и h момент сопротивления сечения относительно горизонтальной оси не изменится при повороте его на 45⁰?

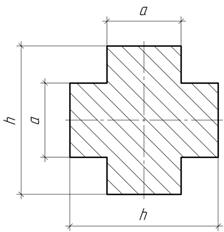
Задача 52.

Из квадрата вырезается равнобедренный треугольник АВС. Найти высоту треугольника по условию, чтобы его вершина совпадала с центром тяжести оставшейся части.

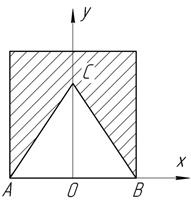
Ответ: У_с=0,634а.

Задача 53.

Прямоугольник шириной l и высотой h разделен на две части квадратной параболой у=ах². Определить площади и координаты центров тяжести образовавшихся при этом криволинейных треугольников.

Ответ: А₁=hl/3,

Задача 54.

Найти момент инерции треугольника АВС относительно оси х, если известны координаты его вершин: А(0;0), В(b,2b), С(2b,b).

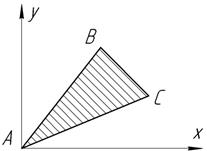
Ответ: I_х=7b⁴/4.

Задача 55.

Найти момент инерции треугольника АВС относительно оси х, если известна его площадь А=12 см² и даны b=h6 см и С=4 см.

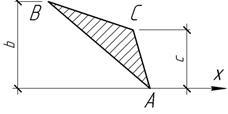
Ответ: I_х=126 см⁴.

Задача 56.

Найти осевой момент инерции круга, имеющий 8 одинаковых вырезов, равномерно расположенных по окружности, если R₁=0,5R, R₂=0,75R.

Ответ: I_х=0,69 R⁴.

Задача 57.

Найти осевой момент инерции для круга, ослабленного отверстиями в форме равносторонних треугольников со стороной, равной R/4.

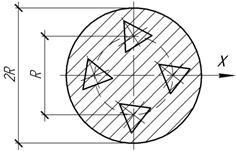
Ответ: I_х=0,77 R⁴.

Задача 58.

Стержень квадратного сечения выполнен из материала с капиллярами, ориентированными вдоль оси стержня и равномерно распределенными по площади сечения с коэффициентом пористости К=А_кап/А_брутто=0,25. Определить размер сечения, для которого I_х=10000 см⁴.

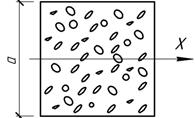
Ответ: а=20 см.

Задача 59.

Для прямоугольника со сторонами b=2 см, h=3 см определить положение главных осей, проходящих через точку О, и вычислить главные моменты инерции.

Ответ:

Задача 60.

Определить момент инерции полукруга радиуса r относительно оси

Ответ:

Задача 61.

Покажите, что для прямоугольного сечения с отношением сторон h/b=2 любые оси, проведенные через середину одной из длинных сторон, являются главными.

Задача 62.

Требуется доказать следующее положение: если для множества осей, проходящих через какую-либо точку, можно указать более одной пары несовпадающих главных осей, то вообще все оси, проходящие через эту точку, являются главными.

Задача 63.

Найти осевые и центробежный моменты инерции равнобедренного прямоугольного треугольника относительно осей ху, проходящих через середину гипотенузы.

Ответ: I_x=I_y=a⁴/24, I_xy=0.

Задача 64.

Доказать, что при любом значении размера а главная центральная ось сечения, состоящего из двух одинаковых уголков, проходит через их центры тяжести.

Задача 65.

Для заданного сечения найти главные оси, проходящие через точку О.

Ответ: Все оси, проходящие через точку О, так как I_х=I_у.

Задача 66.

Сечение образованно равносторонним треугольником и прямоугольником. Доказать, что величина момента инерции относительно оси, проходящей через центр тяжести треугольника, не зависит от направления оси.

Задача 67.

При каком значении высоты h равнобочной трапеции все оси, проходящие через точку О основания трапеции, будут главными?

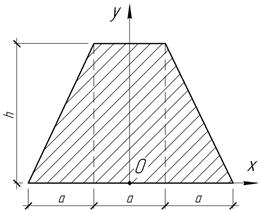
Ответ: h/a=1,29.

Задача 68.

Определить положение главных центральных осей тонкостенного сечения. Толщина стенки постоянна, мала и равна t. Размеры даны по средней линии сечения.

Ответ: Одна из главных осей проходит через центры тяжести угольников (по линии С₁С₂).

Задача 69.

Для прямоугольника с отношением сторон h/b=2 найти точку К, обладающая тем свойством, что все проходящие через нее оси являются главными.

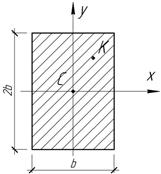
Ответ:

Задача 70.

Балка состоит из 16 стержней прямоугольного сечения 5х10 мм, расположенных по цилиндрической поверхности радиуса r=100 мм. Стержни связанные друг с другом с помощью колец, расположенных на некотором расстоянии по длине цилиндра, благодаря чему можно рассматривать указанную конструкцию как единое целое. Найти момент сопротивления W_х.

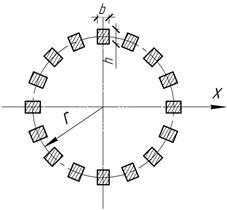
Ответ: W_х=38 см³.

Задача 71.

При каком соотношении между размерами h и а момент сопротивления крестообразного сечения относительно горизонтальной оси не изменится при повороте его на 45⁰?

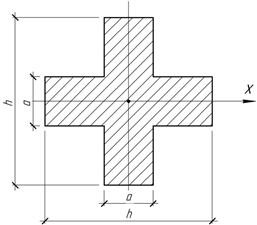
Ответ: h/а=2,414.

Задача 72.

При каком соотношении размеров крестообразного сечения удаление верхнего и нижнего ребер приводит к увеличению момента сопротивления сечения относительно центральной горизонтальной оси х?

Ответ: b/t>(H/h)³/[(H/h)-1].

Задача 73.

Для произвольной плоской фигуры найти геометрическое место точек, относительно которых сечение имеет одинаковую величину полярных моментов инерции.

Ответ: Семейство концентрических окружностей с центром, совпадающим с центром тяжести плоской фигуры.

Задача 74.

Определить центр тяжести поперечного сечения, изображенного на рисунке.

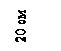
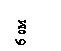
Ответ: х_с = 10,57 см; у_с = 9,43 см. (Центр тяжести С поперечного сечения должен лежать на оси симметрии поперечного сечения).

Задача 75.

Определить положение центра тяжести составного сечения, показанного на рис. 1.

Вычислить статические моменты S_x, S_y сложного составного сечения (рис.2). Определить площадь этого сечения и найти координаты его центра тяжести.

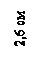
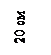
Решение к рис 2. Предлагается следующий порядок решения.

Если поперечное сечение не содержит осей симметрии, то случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте. Каждому прокатному профилю присваивается порядковый номер.

Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i – го профиля относительно случайных осей х, у; А_i – площадь сечения i–го профиля, А – площадь поперечного сечения всего составного сечения, n – число профилей.

Затем вычисляются статические моменты всего сечения по формулам

а по формулам находятся координаты центра тяжести.

Следуя предложенной методике, выпишем (рис. 2): А₁ = 6,36 см²; А₂ = 23,4 см²; А₃ = 26,8 см²; А = 56,56 см²; х₁ = 3,87 см; х₂ = 7,07 см; х₃ = 17,6 см; у₁ = 17,4 см; у₂ = 10 см; у₃ = 10 см.

По формулам

Находим

S_x=6,36∙17,4+23,4∙10+26,8∙10=612,66 см³;

S_y=6,36∙3,87+23,4∙7,07+26,8∙17,6=661,73 см³.

И наконец, с помощью формул определяем координаты центра тяжести всего сечения:

Для проверки полученных результатов рекомендуем самостоятельно определить координаты центра тяжести составного сечения относительно осей p, q (рис. 2).

Ответ к рис.1: x_c = 11,7 см; y_c = 10,83 см.

Ответ к рис.2: x_c = 0; y_c = 10,83 см.

Задача 76.

Вычислить координаты центра тяжести составного сечения, состоящего из швеллера и уголка (рис. 1)

Вычислить координаты центра тяжести сложного составного сечения, изображенного на рис. 2.

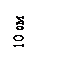
Ответ к рис 1: х_с = 7,74 см; у_с = 6,76 см.

Ответ к рис 2: х_с = 0; у_с = 9,23 см.

Задача 77.

Определить статические моменты, осевые моменты инерции, центробежные моменты инерции и положение главных осей неравнополочного уголка 120×80×10 относительно осей х, у и относительно центральных осей х_с, у_с в четырех вариантах (рис. а, б, в, г). Вычислить положение центра тяжести. Для вычислений принять b = 8 см, h = 12 см, t = 1 см.

Ответ: а) S_x = 75,5 см³; y_c = 3,97 см; S_y = 37,5 см³; x_c = 1,97 см;

I_x = 578,32 см⁴, I_y = 174,32 см⁴; I_xy = 51,75 см⁴; tg2α = 1,0928;

I_xc = 278,32 см⁴, I_yc = 100,31 см⁴; I_xcyc = -97,26 см⁴; α = 23,8°.

Задача 78.

Найти положение центра тяжести поперечного сечения железобетонной балки (см. рис.). Вычислить главные моменты инерции относительно главных осей х_с, у.

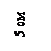
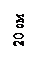
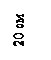
Указания. Для расчета использовать материалы предыдущего примера, в котором определены главные моменты инерции сечения в виде равнобокой трапеции. В рассматриваемом случае необходимо принять a = 20 см, h = 20 см, b = 40 см, тогда для трапециевидной части поперечного сечения балки будем иметь

A₁=600 см²;

Ответ: y_c = –1,7 см; I_y = 116667 см⁴.

Задача 79.

Найти положение центра тяжести площади поперечного сечения, представленного на рис. 1. Определить главные моменты инерции этого сечения.

Вычислить главные моменты инерции для сечения, показанного на рис. 2.

Вычислить главные моменты инерции поперечного сечения круглого бревна диаметром d и прямоугольного сечения бруса с b= d/2, выполненного из этого бревна (рис. 3). Найти высоту h прямоугольного сечения бруса.

Ответ к рис.1:

Ответ к рис.2: I_y = I_max = 1172,62 см⁴; I_min = 122,11 см⁴.

Ответ к рис.3: I_x = I_y = 0,049087d⁴ (для круглого поперечного сечения), I_x = 0,02706d⁴; I_y = 0,009021d⁴ (для прямоугольного поперечного сечения).

Задача 80.

Найти положение центра тяжести С и вычислить главные моменты инерции поперечного сечения участка стены таврового сечения (см. рис. 1). Кладка выполнена из глиняного кирпича пластического прессования на растворе.

Найти положение центра тяжести и вычислить момент инерции для поперечного сечения, изображенного на рис. 2.

Определить главные моменты инерции поперечного сечения, показанного на рис. 3.

Ответ к рис.1: х_с = 0,44 м;

Ответ к рис.2:

Ответ к рис.3: I_x = 26086 см⁴; I_y = 3898 см⁴.

Задача 81.

Вычислить главные моменты инерции для составного поперечного сечения, изображенного на рис.1.

Вычислить главные моменты инерции для составного поперечного сечения, представленного на рис. 2. Найти положение главных осей инерции.

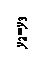
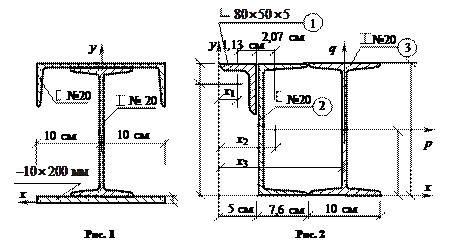
Ответ к рис.1: I_max = 5828,4 см⁴; I_min = I_у = 2301,7 см⁴.

Ответ к рис.2: х_с = 11,7 см; у_с = 10,83 см; = 0,4642; α= 12^о27^/; I_max = 3795 см⁴; I_min = 1981 см⁴;

Задачи 82-90.

Найти координаты центра тяжести и вычислить главные моменты инерции для составных поперечных сечений, показанных на рис. 1 – 9.

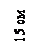
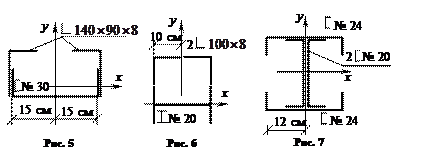
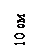
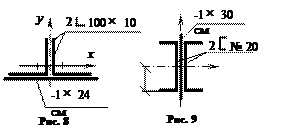
Ответ к рис. 1: х_с = 0; у_с = 3,8 см;

Ответ к рис. 2: х_с = 0; у_с = 7,05 см;

Ответ к рис. 3: х_с = 0; у_с = –4,54 см;

Ответ к рис. 4: х_с = 0; у_с = 2 см;

Ответ к рис. 5: х_с = 0; у_с = 3,3 см;

Ответ к рис. 6: х_с = 0; у_с = 6,6 см;

Ответ к рис. 7: х_с = 0; у_с = 0; I_x = 7411 см⁴; I_y = 622,5 см⁴.

Ответ к рис. 8: х_с = 0; у_с = –1,3 см; I_min = 524 см⁴; I_y = I_max = 1818 см⁴.

Ответ к рис. 9: х_с = у_с = 0; I_x = 5290 см⁴; I_y = 537,6 см⁴.

Онлайн-калькулятор "Расчет геометрических характеристик равнобедренного треугольника"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00