Главная

Лекция 4 (продолжение). Примеры решения задач по геометрическим характеристикам плоских сечений

Геометрические характеристики сложных сечений

Пример 1.

Сечение стержня представляет собой несимметричную фигуру, показанную на рис. 1. Требуется найти положение главных центральных осей инерции фигуры и моменты инерции относительно этих осей.

Рис.1

Решение.

Найдем положение центра тяжести фигуры по формулам ; . Разобьем фигуру на три простые: треугольник I, прямоугольник II и квадрант круга Ш. Площадь всей фигуры

Для определения статических моментов выберем вспомогательные оси , проходящие через центр тяжести прямоугольника II (рис. 2). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат . Суммарные статические моменты

Координаты центра тяжести

отложены на рис. 2.

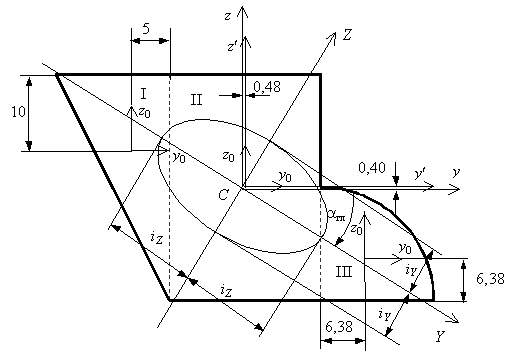
Рис.2

Проведем через центр тяжести центральные оси (см. рис. 2) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и Ш используем формулы , , . Моменты инерции относительно собственных осей прямоугольника, треугольника и квадранта круга вычисляем соответственно по формулам

; ; ,

; ; .

; .

Отсюда

Теперь найдем положение главных осей инерции. Угол, на который надо повернуть ось , чтобы она стала главной осью, определяем по формуле :

;

; .

В соответствии с правилом знаков откладываем отрицательный угол по часовой стрелке и проводим главные центральные оси инерции Y, Z (см. рис. 2). Вычислим моменты инерции относительно этих осей по формуле :

; .

Для проверки вычислений удобно использовать следующее свойство: сумма моментов инерций относительно двух любых пар ортогональных осей есть величина постоянная. Тогда должно быть

.

В нашем примере .

Чтобы выяснить, какой момент инерции – максимальный или минимальный соответствует оси , исследуем знак второй производной функции по формуле .

.

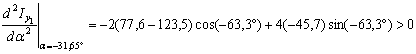Положительный знак второй производной означает, что оси соответствует минимальное значение момента инерции, т. е.

Найдем радиусы инерции относительно главных центральных осей по формуле и построим эллипс инерции.

Эллипс инерции показан на рис. 2. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура.

Пример 2.

Определить координаты центра тяжести и осевые моменты инерции сечения в виде круга радиусом r =3а с круговым отверстием радиуса r₀ = a, касающимся центра круга (см. рис.).

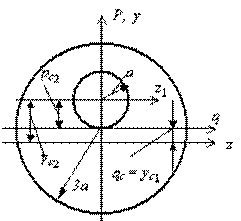
Решение.

Принимаем за 1-й элемент сплошной круг радиусом r =3а, за второй элемент отверстие радиуса r₀ = a. Начальные оси проводим через центр тяжести 1-го элемента.

Тогда имеем:

; ;

; ; .

Так как ось р является осью симметрии сечения, так же как и осями симметрии элементов сечения, то эта ось является центральной осью у и . Следовательно, для определения положения центра тяжести сечения требуется определить только координату р_с

.

Координаты центров тяжести элементов относительно центральных осей:

; ; ; .

Осевые моменты инерции круга относительно собственных центральных осей определяются по формуле

.

Следовательно, имеем:

; .

Определяем осевые моменты инерции сечения

;

.

Так как сечение имеет ось симметрии, то центробежный момент инерции сечения равен нулю и оси у, z являются главными.

Пример 3.

Для фигуры, показанной на рис.1 определить положение главных осей инерции и главные моменты инерции.

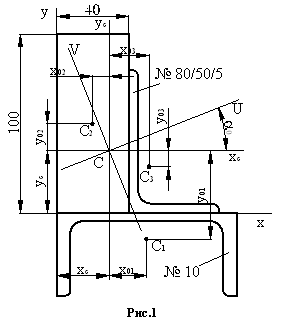
Решение.

Выписываем основные исходные данные для каждой фигуры

Швеллер

S₁ = 10,9 см² ; I_x = 20,4 см⁴; I_y = 174 см⁴; y₀ = 1,44 см; h = 10 см

Неравнополочный уголок

S₃ = 6,36 см²; I_x = 41,6 см⁴; I_y = 12,7 см⁴; I_min = 7,58 см⁴; = 0,387; x₀ = 1,13 см; y₀ = 2,6 см

Прямоугольник

S₂ = 40 см²

см⁴.

см⁴.

Вычерчиваем сечение в масштабе

Проводим произвольные оси координат

Определяем координаты центра тяжести сечения

см;

см.

Проводим центральные оси

см, см,

см,

см, см,

см.

Определяем осевые моменты инерции относительно центральных осей

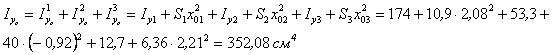
Определяем центробежный момент инерции относительно центральных осей

Центробежный момент инерции для угловой прокатной стали относительно ее центра тяжести определяется по одной из следующих формул:

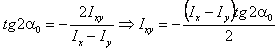
см⁴.

Знак центробежного момента инерции для угловой прокатной стали определяется согласно рис. 2, поэтому I_xy3 = -13,17 см⁴.

Определяем положение главных осей инерции

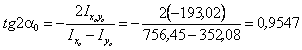
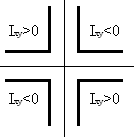
Рис.2

Определяем главные моменты инерции

Пример 4.

Определить координаты центра тяжести сечения (рис.1), составленного из прокатных профилей.

Рис.1

Решение:

Из таблиц сортамента имеем:

для швеллера № 22а: Z_o = 2,46 см; А₁ = 28,8 см²;

для уголка 100х100х10: Z_o = 2,83 см; А₂ = 19,2 см².

Совмещаем вспомогательные оси u и v с центральными осями швеллера и выполняем вспомогательные вычисления в табличной форме

Рис.2

Номер вычисления	Координаты, см		Площадь Ai, cм^2	Статические моменты, см^3
	ui	vi		uiAi	viAi
1 2	0 5,29	0 8,17	28,8 19,2	0 101,6	0 156,9

Координаты центра тяжести

см,

см.

Пример 5.

Определить положение главных центральных осей и величины главных центральных моментов инерции данного сечения (см. рис.1).

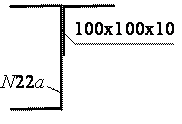
Рис.1

Рис. 2

Решение.

1. Определение моментов инерции относительно центральных осей хСy.

По таблице сортамента имеем:

швеллер № 22: = 2330 cм⁴, = 187 cм⁴, А₁ = 28,8 см²;

уголок 100х100х10: = 179 cм⁴, А₂ = 19,2 см²;

центробежный момент инерции уголка относительно = 105 cм⁴.

Учитывая, что центральные оси xy проведены параллельно собственным осям элементов фигуры, для вычисления осевых и центробежного моментов инерции всего сечения воспользуемся формулами, представляя все необходимые вычисления в табличной форме:

Номер элемента	Координаты центра тяжести, см		Площадь Аi, см^4	Моменты инерции площадей, см^4
	xi	yi				Ixi			Iyi		xiyiAi	Ixiyi
1	-2, 12	-3, 27	28,8	2330	308	2638	187	129	316	0	200	200
2	3, 17	4, 90	19,2	179	461	640	179	193	372	105	298	403
			48	2509	769	3278	366	322	688	105	498	603

2. Определение главных центральных моментов инерции сечения. По формуле имеем

,

Отсюда I_max = I₁ = 3412 см⁴, I_min = I₂ = 555 см⁴.

Ориентация максимальной главной оси определяется по формуле

= (3278-3412)/603 = -0,222,

откуда = -12°30'.

3. Построение эллипса инерции. Главные радиусы инерции равны

см;

см.

Отложив радиусы инерции перпендикулярно к соответствующим осям в том же масштабе, в каком вычерчена фигура, строим на них, как на полуосях, эллипс инерции.

Пример 6.

Для сложных составных поперечных сечений, не содержащих осей симметрии, предлагается следующий порядок расчета.

1) Сначала вычерчивается поперечное сечение. Случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте (рис.1). Каждому прокатному профилю присваивается порядковый номер. Наносим местные оси координат х_i, у_i, проходящие через известные центры тяжести i–го профиля. Оси х_i, у_i параллельны случайным осям х, у соответственно.

2) Наносим на рисунок известные размеры сечения, взятые из задания или из соответствующих таблиц сортамента прокатной стали.

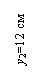
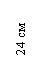
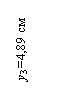
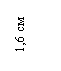
3) Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i–го профиля относительно случайных осей х, у; А_i – площадь сечения i–го профиля, – площадь поперечного сечения всего составного сечения; – осевые и центробежные моменты инерции i–го профиля относительно местных осей х_i, у_i.

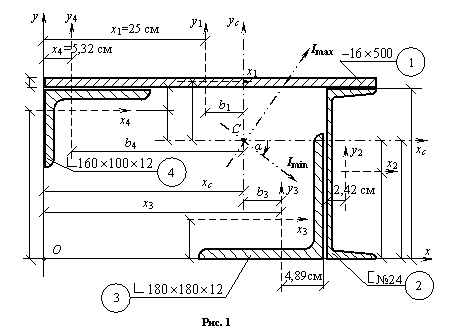
4) Следуя предложенной методике, выпишем геометрические характеристики для поперечного сечения, изображенного на рис. 1:

х₁ = 25 см; х₂ = 43,42 см; х₃ = 36,11 см; х₄ = 5,32 см;

у₁ = 24,8 см; у₂ = 12 см; у₃ = 4,89 см; у₄ = 21,64 см;

5) С помощью формул

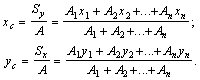
находим координаты центра тяжести всего поперечного сечения:

6) Наносим оси х_с, у_с, которые проходят через центр тяжести С всего составного поперечного сечения и определяем расстояния между осями х_с и х_i, а также между осями у_с и у_i:

а₁ = у₁ – у_с = 24,8 – 17,5 = 7,3 см; b₁ = х₁ – х_с = 25 – 27,4 = –2,4 см;

а₂ = у₂ – у_с = 12 – 17,5 = –5,5 см; b₂ = х₂ – х_с = 43,42 – 27,4 = 16,02 см;

а₃ = у₃ – у_с = 4,89 – 17,5 = –12,61 см; b₃ = х₃ – х_с = 36,11 – 27,4 = 8,71 см;

а₄ = у₄ – у_с = 21,64 – 17,5 = 4,14 см; b₄ = х₄ – х_с = 5,32 – 27,4 = –22,08 см.

7) Используя формулы получаем выражения для вычисления осевых моментов инерции относительно центральных осей х_с и у_с всего поперечного сечения:

или окончательно:

По формуле находим значение центробежного момента инерции относительно осей х_с, у_с:

где, согласно рис. 1, имеем так как швеллер и полоса имеют оси симметрии х₂ и х₁, у₁ соответственно.

Для вычисления для равнополочного уголка предварительно выпишем из таблицы сортамента «Уголки стальные горячекатаные равнополочные» = 2093 см⁴,= 540 см⁴,, (рис. 2, а).

Тогда формула принимает вид:

Для вычисления для неравнополочного уголка (рис. 2, б) предварительно выпишем из таблицы сортамента

= 238,75 см⁴, = 784,22 см⁴, I_uv = 0, I_u = 142 см⁴, = 0,388

и затем, согласно формуле получаем:

Таким образом, формула для рассматриваемого случая принимает вид:

где = 0,388; = –21^о12^/ (рис.2, б), тогда

Значение центробежного момента можно вычислить, используя формулу . Для этого рассмотрим рис. 2, в. Разобьем уголок на два прямоугольника с

и .

В этом случае по формуле получаем

Как видно, результаты очень близки по значениям.

Теперь можно приступить к определению центробежного момента всего составного сечения относительно осей хс, ус:

8) Главные оси инерции можно построить, повернув центральные оси х_с, у_с на угол (рис. 1):

9) Величины главных моментов инерции определяем по формуле

Окончательно получаем, что I_max = 48582 см⁴, I_min = 13438 см⁴.

Полученные значения удовлетворяют условию :

Таким образом, определены все геометрические характеристики сложного составного поперечного сечения, показанного на рис.1.

Пример 7.

Определить положение главных центральных осей и вычислить главные центральные моменты инерции для сечения (см. рис.), состоящего из неравнобокого уголка №14/9 (ГОСТ 8510-57) и швеллера №24 (ГОСТ 8240-56).

Решение.

Разбиваем фигуру на части, геометрические характеристики которых можно взять из таблиц сортамента, на швеллер и уголок; через их центр тяжести c₁ и c₂ проводим центральные оси z₁, y₁ и z₂, y₂, параллельные их сторонам. Поскольку z₁ - ось симметрии швеллера, то она и ось y₁ являются его главными центральными осями. Главная центральная ось уголка v-v образует с его центральной осью z₂ угол .

Из таблиц сортамента имеем:

Для швеллера №24 F₁=30,6 см²

координаты центра тяжести

h=24 см b=9 см

Для уголка №14/9 F₂=22,2 см²

координаты центра тяжести

1) Определим координаты центра тяжести всего сечения, для этого принимаем за исходные оси главные центральные оси швеллера z₁ и y₁ и согласно (4.4) получаем:

Через центр тяжести C проводим центральные оси z_c и y_c, параллельные проведенным ранее центральным осям швеллера и уголка.

Для проверки правильности определения координат центра тяжести, вычислим статические моменты относительно центральных осей z_c и y_c, которые должны быть равны нулю.

Получаем:

2) Вычислим осевые и центробежный моменты инерции всего сечения в системе центральных осей z_c, y_c по формулам:

для швеллера , т.к. оси z₁ и y₂ являются для швеллера главными центральными; для уголка согласно сортамента.

3) Определяем угол наклона главных центральных осей u и v относительно центральных осей z_c, y_c:

Поскольку угол отрицательный, он откладывается по ходу часовой стрелки, а т.к. , то поворотом оси z на угол, меньший 45°, мы получим направление главной центральной оси u, относительно которой главный момент инерции максимален I_u=I_max.

4) Главные моменты инерции определяем по формулам

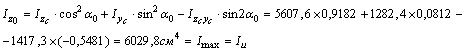
Проверки: а) Определяем центробежный момент инерции относительно главных центральных осей , который должен быть равен нулю:

б) Определим главные центральные моменты инерции I_u и I_v по формулам:

I_u=I_max=3445,0 + 2585,6 = 6030,6 см⁴

I_v=I_min=3445,0 - 2585,6 = 859,4 см⁴

Максимальное расхождение составляет:

.

в) Должно удовлетворяться условие:

Расхождение составляет:

.

5. Определение моментов сопротивления сечения.

Наиболее удаленными точками от осей u и v являются точки A и B:

y_B = y_A = -17,94 см

По формулам получаем:

6. Радиусы инерции вычисляются по формулам (4.35), (4.36):

F = F₁ + F₂ = 30,6 +22,2 = 52,8 см²

Откладывая отрезки i_u=10,69 см и i_v=4,03 см перпендикулярно соответствующим осям, строим на них, как на полуосях, эллипс инерции (см. рис.).

Пример 8.

Для поперечного сечения (см. рис.1), состоящего из двутавра №10 и равнобокого уголка 50х50х5 мм, требуется:

1) определить положение центра тяжести сечения;

2) найти центральные осевые и центробежный моменты инерции сечения;

3) определить направление главных центральных осей инерции сечения (U и V);

4) вычислить главные центральные моменты инерции сечения.

Рис.1

Решение.

1. Выписываем из таблиц сортамента прокатных профилей необходимые для расчета данные:

- Двутавр №10 (ГОСТ 8239-56);

A₁ =12 см²; b=5,5 см; h=10 см; I_x= 198 см⁴; I_y1= 17,9 см⁴.

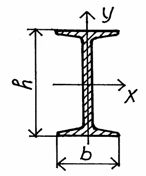
- Уголок равнобокий 50х50х5 (ГОСТ 8509-57);

A= 4,8 см²; b = 5 см; z₀= 1,42 см; I_x= 11,2 см⁴ ; I_x0= 17,8 см⁴ ; I_y0= 4,63 см⁴

2. Вычерчиваем в масштабе сечение. Для определения положения центра тяжести составного сечения обозначим двутавр – I и равнобокий уголок – II и проведем собственные центральные оси X₁, Y₁ и X₂, Y₂. Проводим вспомогательные оси X, Y. Тогда координаты центра тяжести сечений I и II относительно осей X, Y:

см;

см;

см;

см.

Координаты центра тяжести всего сечения:

где А₁ =12 см²; А₂ =4,8 см² – площади поперечных сечений.

Наносим эти размеры на чертеж и через полученный центр тяжести С проводим центральные оси X_c и Y_c. Проверяем правильность вычислений: центр тяжести составного сечения должен лежать на линии, соединяющей центры тяжести первого и второго сечений.

3. Вычисляем центральные осевые и центробежный моменты инерции составного сечения. Воспользуемся формулами для определения моментов инерции при параллельном переносе осей:

; ;

; ; (1)

; .

где m₁, m₂ – расстояние между параллельными осями X₁ и Х_С, X₂ и Х_С соответственно;

n₁, n₂ – расстояние между параллельными осями Y₁ и Y_c, Y₂ и Y_c соответственно.

На основании данных чертежа получим:

= 2,75 – 2,37 = 0,38 см;

= –(2,27 – 1,42) = –0,95 см;

= –(6,83 – 5) = –1,83 см;

= 11,42 – 6,83 = 4,59 см.

Вычисляем центральные осевые моменты инерции всего сечения, равные сумме моментов инерции фигур, составляющих это сечение, с учетом формулы (1):

= (17,9 +0,38²×12) +(11,2 + (– 0,95)²×4,8) = 19,63 + 15,53 = 352 см⁴; (2)

= (198 + (– 1,83)²×12) +(11,2 + 4,59²×4,8) = 238,2 + 111,9 = 350,1 см⁴. (3)

Центробежный момент инерции составного сечения вычисляем с учетом формул (1) аналогично:

=

= (0 + 0,38×(–1,83)×12) + (– 6,58 + (– 0,95)×4,59×4,8) = (– 8,34) + (– 27,5) = – 35,8 см⁴. (4)

В этой формуле для двутавра, являющегося симметричным сечением относительно собственных центральных осей, центробежный момент инерции = 0, т.к. эти оси - главные центральные оси двутавра. Для равнобокого уголка (= 45º):

;

Рис.2

Знак I_xy при различных положениях равнобоких и неравнобоких уголков выбирается согласно рисунок 2. В нашем случае берется знак минус.

4. Определим направление главных центральных осей на основании вычислений по формулам (2), (3) и (4):

= –12º48’; = –6º24’.

Угол < 0, поэтому угол = –6º24’ отложим от оси Х_С в направлении часовой стрелки и проведем главную ось U, а ей перпендикулярно – главную ось V (рис. 2).

5. Вычислим значения главных центральных моментов инерции

I_max = 354 см⁴ = 354·10^-8 м⁴;

I_min = 31,2 см⁴ = 31,2·10^-8 м⁴.

Положение оси U(I_min) легко определить, т.к. эта ось, во-первых, пересекает сечение по наибольшему протяжению и, во-вторых, располагается ближе к той центральной оси инерции (оси Х_С), относительно которой центральный момент инерции имеет меньшую величину, т.е. (I_xc<I_yc).

Таким образом I_V = I_min = 31,2·10^-8 м⁴,

I_U = I_max = 354 см⁴ = 354·10^-8 м⁴.

Проверка: ;

см⁴;

см⁴.

Т.к. оси V и U главные, то должно выполняться условие равенства нулю центробежного момента инерции, вычисленного относительно главных осей V и U, т.е. = 0. Тогда при = –6º25’ получим:

где ,

.

Пример 9.

Задано составное сечение, состоящее из двутавра № 20, неравнобокого уголка 100х63х6 мм и пластины 240х20 мм. На рис. 1 представлено это сечение.

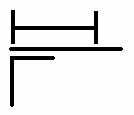
Рис.1

Требуется:

1. Определить центр тяжести сечения.

2. Вычислить осевые и центробежные моменты инерции сечения относительно центральных осей.

3. Определить положение главных центральных осей инерции сечения.

4. Вычислить главные центральные моменты инерции сечения.

Решение.

Вычерчиваем сечение в масштабе на листе чертежной или миллиметровой бумаги. Обозначим отдельные элементы: I - двутавр; II – пластина; III – неравнобокий уголок (рис. 2). Затем проводим центральные оси каждого сечения X₁, Y₁; X₂, Y₂ и X₃, Y₃.

Из сортамента выписываем все необходимые для расчета данные:

1. Двутавр №20 (ГОСТ 8239 – 89).

Как видим из чертежа (рис.2), двутавр расположен горизонтально, а в сортаменте – вертикально. По этой причине принимаем осевые моменты инерции 115 см⁴, 1840 м⁴,

b₁ = h = 20 см, h₁ = b = 10 см, где J_x, J_y, h и b – числовые данные из сортамента. Площадь поперечного сечения А₁ = 26,8 см².

2. Пластина (прямоугольник): b₂ = 16 см; h₂ = 2 см.

см².

3. Уголок неравнобокий 100х63х6 мм (ГОСТ – 8510 – 86):

А₃ = 9,58 см³; = 98,3 см⁴; = 30,6 см⁴; = 18,2 см⁴;

х₀ = 1,42 см; у₀ = 3,23 см; = 0,393; b₃ = 0,3 см; h₃ = 10 см.

Рис.2

1. Определение центра тяжести сечения. Выбираем в качестве вспомогательных осей – оси уголка х₃, у₃. Определяем относительно этих осей координаты центров тяжести сечений:

- для двутавра: х₁ = b₁/2 – х₀ = 20/2 – 1,42 = 8,58 см;

у₁ = у₀ + h₂/2+h₁/2 = 3,23 + 2/2+11/2 = 9,73 см;

- для пластины: х₂ = b₂/2 – х₀ = 24/2– 1,42 = 10,58 см;

у₂ = у₀ + h₂/2 = 3,23 +2/2 = 4,23 см;

- для уголка: х₃ = 0; у₃ = 0.

Вычисляем координаты центра тяжести составного сечения по формулам:

Откладываем от вспомогательных осей х₃, у₃ координаты центра тяжести х_С, у_С и через полученную точку С проводим центральные оси Х_С и Y_С параллельно вспомогательным осям.

2. Вычисление осевых (, ) и центробежного () моментов инерции сечения относительно центральных осей (X_С , Y_С). Применим формулы для вычисления моментов инерции составного сечения при параллельном переносе осей:

= (115 + 4,23²×26,8) + (16 + (-1,27)²×48) + (98,3 + (-5,50)²×9,58) =594 + 93,4 + 388 = 1075 см²,

где n₁, n₂ и n₃ – расстояния от центральной оси Х_С до осей х₁, х₂ и х₃, соответственно. Т.е. имеем:

n₁ = у₁ – у_С = 9,73 – 5,50 = 4,23 см;

n₂ = -(у_С – у₂) = -(5,50 – 4,23) = -1,27 см;

n₃ = - у_С = -5,50 см.

= (1840 + (-0,16)²×26,8) + (2304 + 2,04²×48) + (30,6 + (-8,74)²×9,58) = 1841 + 2504 + 762 = 5107 см⁴,

где m₁, m₂ и m₃ – расстояние от центральной оси Y_С до осей у₁, у₂ и у₃, соответственно. Т.е. имеем:

m₁ = -(х_С – х₁) = -(8,74 – 8,58) = -0,16 см;

m₂ = х₂ – х_С = 10,58 – 8,74 = 2,04 см;

m₃ = -х_С = -8,74 см.

=(0 + 4,23×(-0,16)×26,8) + (0 + (-1,27)×2,04×48) + (31,5 + (-5,50)×(-8,74)×9,58) = -18,1 – 124,3 + 400 = 318 см⁴.

При вычислении центробежного момента инерции следует учесть, что для симметричных сечений (двутавр, швеллер, пластина) центробежные моменты инерции относительно их собственных центральных осей равны нулю, т.к. оси симметрии являются главными осями. Тогда , .

Для неравнобокого уголка ось U₃ и ось V₃, проведенная нами через центр тяжести О₃ перпендикулярно первой оси, являются главными центральными осями уголка (см. рис.2). Следовательно, центробежный момент инерции уголка относительно этих осей равен нулю.

Оси х₃, у₃ не являются главными центральными осями. Поэтому . Для его вычисления воспользуемся известной формулой:

При этом для вычисления неизвестного главного момента инерции воспользуемся зависимостью:

Для определения угла a из сортамента имеем . Тогда .

Угол в данном случае положителен, т.к. поворот главных центральных осей V₃, U₃ до совмещения их с осями х₃, у₃ выполнен против часовой стрелки (см. рис.2).

Для определения знака центробежного момента инерции для равнобоких и неравнобоких уголков в зависимости от их положения удобно пользоваться также данными рис.3.

Рис.3

Рис.2.3.

3. Определение положения главных центральных осей инерции.

Определяем угол по формуле:

Рисунок 3

Откладываем от оси X_С угол против часовой стрелки и проводим взаимно перпендикулярно главные оси для составного сечения U и V, соответственно.

4. Вычисление главных центральных моментов инерции. Для их вычисления используем формулу:

J_max = 5104 см⁴; J_min = 1050 см⁴.

Т.к. , то , а .

Для проверки правильности расчетов воспользуемся формулой для вычисления центробежного момента инерции. Вычислим его относительно главных центральных осей U и V (J_UV = 0):

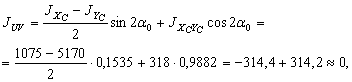
где ;

Ошибка в инженерных расчетах не должна превышать . Проверяем расчеты по формуле:

Пример 10.

Для составного поперечного сечения стержня, состоящего из равнобокого уголка № 7 с толщиной стенки 8 мм, швеллера №22 и полосы 180х20 мм (см. рис.1), требуется найти положение центра тяжести сечения, направление главных центральных осей инерции u и v, а также вычислить главные центральные моменты инерции I_max и I_min.

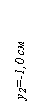
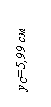
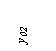
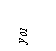
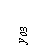
Рис.1

Решение.

1. Определяем координаты центра тяжести поперечного сечения.

Размеры и геометрические характеристики уголка и швеллера устанавливаем по сортаментам. Вычерчиваем сечение в масштабе (см. рис. 1). Выбираем оси сравнения x и y, располагая их по контуру швеллера. Именно в этих осях мы и будем определять положение центра тяжести всего сечения. Для каждого элемента сечения (уголка, швеллера и полосы) проводим собственные центральные оси (), параллельные выбранным осям сравнения x и y.

Координаты центра тяжести всего поперечного сечения (точка С), состоящего из трех элементов (уголка – 1, швеллера – 2 и полосы – 3), вычисляются по формулам:

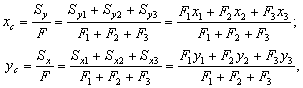
где и – статические моменты соответствующего элемента относительно осей сравнения; – площадь элемента; и – координаты центра тяжести элемента в осях сравнения. Вычисления производим в табличной форме (таблица 1).

Таблица 1. Определение координат центра тяжести поперечного сечения

Номер элемента	Наименование элемента	Площадь элемента , см^2	Координаты центра тяжести элемента		Статические моменты элемента относительно осей сравнения и
			, см	, см	, см^3	, см^3
1	Уголок	10,67	-2,02	17,02	-21,55	181,60
2	Швеллер	26,70	2,21	11,00	59,01	293,70
3	Полоса	36,00	9,00	-1,00	324,00	-36,00
	Все сечение	73,37			361,46	439,30

Координаты центра тяжести поперечного сечения (точка С) в осях сравнения x, y:

см; см.

По найденным значениям и отмечаем на чертеже центр тяжести всего сечения точку С (см. рисунок 1) и проводим центральные оси и .

Заметим, что центр тяжести всей фигуры должен располагаться внутри треугольника, вершинами которого являются центры тяжести элементов поперечного сечения.

2. Вычисляем моменты инерции всего поперечного сечения относительно центральных осей и .

Осевые и центробежный моменты инерции сечения относительно центральных осей определяются по следующим формулам:

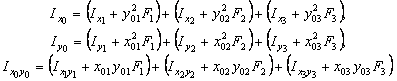
Значения осевых моментов инерции уголка и швеллера относительно собственных центральных осей и определяем по сортаменту. Для полосы осевые моменты инерции соответственно равны:

см⁴; см⁴.

Центробежные моменты инерции швеллера и полосы равны нулю, поскольку их собственные центральные оси являются осями симметрии.

Центробежный момент инерции уголка относительно собственных центральных осей и вычисляется по формуле

,

где и – максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что см⁴, а см⁴.

Центробежный момент инерции уголка не равен нулю, поскольку оси и не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей и на угол 45⁰).

Знак центробежного момента инерции уголка (как, впрочем, и для любой другой фигуры) зависит от направления координатных осей. Он легко определяется следующим образом. Согласно определению, центробежный момент инерции фигуры равен интегралу, в котором элементарная площадка умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,

см⁴.

Теперь определяем координаты центров тяжести отдельных элементов C_i в центральных осях и :

для уголка

см;

см;

для швеллера

см;

см;

для полосы

см;

см.

Дальнейшие вычисления моментов инерции всего поперечного сечения относительно центральных осей и производим в табличной форме (таблица 2).

Таблица 2. Определение моментов инерции сечения относительно центральных осей и

Номер элемента	Наименование элемента	Площадь элемента , см^2	Моменты инерции относительно собственных центральных осей и			Координаты центра тяжести в осях и
			, см^4	, см^4	, см^4	, см	, см
1	Уголок	10,67	48,16	48,16	28,19	-6,95	11,03
2	Швеллер	26,70	2110,00	151,00	0	-2,72	5,01
3	Полоса	36,00	12,00	972,00	0	4,07	-6,99
	Все сечение	73,37

Продолжение таблицы 2

Наименование элемента	"Переносные" моменты инерции, см^4			Моменты инерции относительно центральных осей и , см^4
Уголок	515,39	1298,12	-817,95	1346,28	563,55	-789,76
Швеллер	197,54	670,17	-363,85	2780,17	348,54	-363,85
Полоса	596,34	1758,96	-1024,17	1770,96	1568,34	-1024,17
Все сечение				5897,41	2480,43	-2177,78

После округления вычисленных значений моментов инерции до трех значащих цифр, окончательно, получим

см⁴; см⁴; см⁴.

3. Определяем положение главных центральных осей инерции u и v.

Угол наклона главных центральных осей u и v к центральным осям и соответственно определяем из следующей формулы:

_.

Отсюда находим, что и .

Откладываем положительное значение угла от оси против хода часовой стрелки и проводим главные центральные оси u и v (см. рисунок 1).

Ось, относительно которой момент инерции максимален, составляет меньший угол с той из центральных осей или , относительно которой осевой момент больше. Поскольку см⁴ больше, чем см⁴, ось u является осью относительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.

4. Вычисляем значения главных центральных моментов инерции и для заданного поперечного сечения.

Значения главных центральных моментов инерции всей фигуры определяются по формуле

.

Тогда

см⁴;

см⁴; см⁴.

Контролем правильности последних вычислений может служить следующее условие:

.

Имеем

, .

Пример 11.

Исходные данные.

Сложное сечение состоит из двух составляющих: 1 – швеллер № 20, 2 – прямоугольник с размерами h₂ = 1 см, b₂ = 12 см. Ось Y проходит через центр тяжести обоих составляющих (рис. а).

Требуется:

1. Привести геометрические характеристики простых составляющих сечения относительно их собственных центральных осей.

2. Вычертить сечение в масштабе с указанием основных размеров в числах и обозначением центральных осей простых составляющих сечения, параллельных вспомогательным осям.

3. Определить координаты центра тяжести всего сечения и построить на чертеже главные центральные оси, параллельные вспомогательным осям.

4. Выполнить проверку правильности выполнения третьего пункта путём вычисления статического момента всего сечения относительно общих центральных осей.

5. Определить значения главных центральных моментов инерции сечения.

6. Определить значения осевых моментов сопротивления (W_X, W_Y).

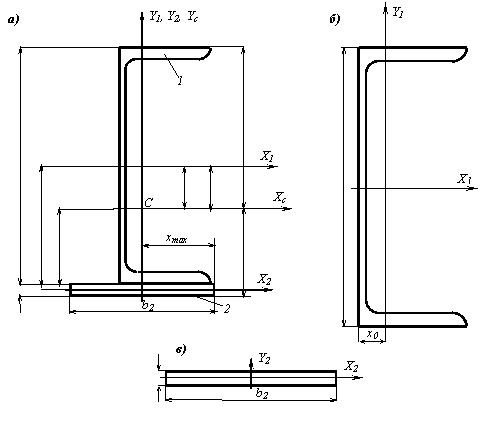
Решение.

1. Геометрические характеристики швеллера относительно его собственных центральных осей (рис. б) согласно ГОСТ 8240-72 следующие:

площадь A₁ = 23,4 см²,

высота сечения h₁ = 20 см,

моменты инерции , ,

абсцисса центра тяжести швеллера .

(ГОСТ прокатных профилей есть в приложениях всех литературных источников, приведённых в списке литературы).

Здесь и далее индекс в нижнем правом углу означает номер простой составляющей сечения. Например, швеллер, согласно принятой в задаче нумерации, имеет номер 1.

Геометрические характеристики прямоугольника относительно его собственных центральных осей (рис. в) следующие:

- площадь ,

- моменты инерции относительно собственных центральных осей

, .

2. Построение сечения в масштабе (см. рисунок 1, а).

3. Определение координаты центра тяжести сечения.

- Строим вспомогательную систему координат. В качестве вспомогательной системы координат выбираем центральные оси швеллера и .

- Определяем координаты центра тяжести сечения относительно вспомогательной системы координат. Для рассматриваемого сечения необходимо вычислить только одну координату , так как другая координата известна. Поскольку центр тяжести всего сечения должен лежать на прямой, соединяющей центры тяжести простых составляющих (это правило действительно для сечений, состоящих их двух частей), то в нашем случае центр тяжести лежит на оси (см. рисунок 1, а), а значит координата .

Координата центра тяжести (к. ц. т.) сечения определяется по формуле:

,

где А – площадь всего сечения; - статический момент всего сечения относительно оси . Для рассматриваемого примера статический момент сечения следует обозначить, как , так как определяется относительно оси .

Рассматриваемое сечение сложное. Для определения статического момента сложного сечения существует формула:

,

где n – число простых составляющих сложного сечения; - статический момент i –й составляющей сложного сечения; , - координата центра тяжести и площадь i –й составляющей сложного сечения. Применительно к нашей задаче формула примет следующий вид:

.

Так как координата y в прямоугольной системе координат представляет собой кратчайшее расстояние (перпендикуляр) от центра тяжести соответствующей фигуры до оси X, то:

, ;

и определены в пункте I. Подставим в формулу полученные значения:

.

Площадь сложного сечения . Тогда для рассматриваемого случая:

.

Следовательно, .

Для случая, когда неизвестной является координата , задача решается аналогично с учётом соответствующих изменений.

- Показываем на чертеже центральные оси всего сечения X_C и Y_C. Причём эти оси строим параллельно вспомогательным осям, как показано на рис. а.

4. Проводим проверку правильности определения центра тяжести сечения.

В основе проверки лежит положение о том, что статические моменты сечения относительно центральных осей равны нулю. Значит, в нашем случае следует вычислить статические моменты сечения относительно полученных центральных осей X_C и Y_C, при этом координаты ц. т. простых составляющих относительно этих осей:

, ;

,

.

Статические моменты сечения относительно осей X_C и Y_C:

.

Иными словами, координаты ц. т. всего сечения вычислены правильно.

5. Определяем главные центральные моменты инерции сечения.

- Вычисляем центробежный момент инерции всего сечения.

Ось - центральная ось всего сечения и , - центральные оси простых составляющих – совпадают. Оси и - главные оси швеллера, значит центробежный момент инерции швеллера относительно них . Оси и - главные оси прямоугольника (так как оси и - оси симметрии прямоугольника), то есть . В этом случае центробежный момент инерции всего сечения в соответствии с формулой изменения центробежных моментов инерции при параллельном переносе осей (см. теорию):

.

- Находим главные оси всего сечения.

Так как центробежный момент инерции сечения относительно главных осей равен нулю, то в нашем случае оси X_C и Y_C - главные оси инерции всего сечения.

- Вычисляем главные центральные моменты инерции всего сечения.

Поскольку главными центральными моментами инерции являются моменты инерции относительно главных центральных осей, то вычисления моментов инерции будем производить относительно осей X_C и Y_C.

Воспользовавшись формулой определения осевых моментов инерции сложного сечения и формулой перехода между параллельными осями для осевых моментов инерции (см. теорию), получим

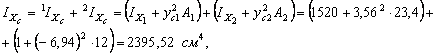
6. Определяем значения осевых моментов сопротивления.

Осевые моменты сопротивления в нашем случае вычисляются по формулам

; ,

где x_max и y_max - расстояния от соответствующих осей до наиболее удалённых точек сечения (см. рис. а).

Здесь: ;

;

.

Тогда: ;

;

.

Пример 12.

Рассмотрим сечение, состоящее из прокатных профилей (см. рис.1).

Рис.1

Решение.

Вычертив в масштабе сечение, нумеруем элементы, с указанием их размерных характеристик – номера двутавра и швеллера, размеры перьев и толщину уголков, высоту и толщину листа.

Проставляем начальные размеры, необходимые для определения положения элементов в сечении – ширина полки двутавра, расстояния до центров тяжестей уголка и швеллера от их граней (из таблицы ГОСТ).

Принимаем положение начальных осей сечения. Пусть горизонтальная ось q проходит через центр тяжести вертикального листа, а вертикальная р – через центр тяжести двутавра. Указываем на чертеже положение начальных осей.

Рассчитываем и указываем на чертеже координаты центров тяжести элементов относительно начальных осей.

р_с = -1,02 см; q_c = 14,76 см.

Определяем осевые , и центробежный моменты инерции элементов относительно собственных центральных осей параллельных начальным осям сечения. Осевые моменты инерции двутавра, швеллера и уголков принимается из таблиц ГОСТ, с учетом положения их осей. Осевые моменты инерции листа (прямоугольное сечение) рассчитываются по формуле , где b - размер параллельный, h – размер перпендикулярный оси, относительно которой вычисляется момент инерции.

Для вертикального листа 60´1,2 (см) (элемент № 2) имеем:

см4; см4.

Центробежный момент инерции в рассматриваемом сечении отличен от нуля только у неравнобокого уголка (элемент № 3) . Согласно ГОСТ 8210-86 для неравнобокого уголка - 20´12,5´1 см⁴; см ⁴; . Согласно рис. 2 угол .

Рис.2. К определению знака угла положения главных осей уголков

Тогда по формуле получим и по формуле : см⁴.

Все данные по элементам сечения - моменты инерции относительно центральных осей элементов и координаты центров тяжестей заносятся в таблицу (см. табл.). Табличная форма позволяет удобно контролировать правильность подготовки исходных данных, от которых зависит корректность дальнейших расчетов.

№ п/п	Тип элемента	А , см^2	, cм^4	, cм^4	, cм^4	pc , см	qc , см	yc , см	zc , см
1.	I № 45	84,7	27696	808	0	22,0	0	23,02	-14,76
2.	| 60´1,2	72,0	8,64	21600	0	0	23,10	1,02	8,34
3.	ë20´12,5´1,2	37,9	482	1568	503	-23,46	19,67	-22,44	4,91
4.	[ № 30	40,5	327	5810	0	-30,00	26,22	- 28,98	11,46
		235,1	28510	29790	503

Вычисляем координаты центра тяжести сечения относительно начальных осей:

см;

см.

7. Определяем координаты центров тяжести элементов сечения относительно центральных осей:

; ;

см; см;

см; см;

см; см;

см; см.

Координаты центров тяжестей элементов записываем в таблицу.

Проводим проверку правильности вычисления координат центров тяжести сечения и его элементов:

; ;

=.

Относительная невязка:

;

.

Определяем осевые, центробежный и полярный моменты инерции сечения относительно центральных осей:

см ⁴;

см ⁴;

см⁴;

см⁴.

Замечание. Результаты расчетов округлялись до четырех значащих цифр.

Определяем положение главных осей:

; ; .

Определяем главные моменты инерции:

(см⁴);

см⁴; см⁴;

или, в соответствии с формулами:

; ;

;

см ⁴; см ⁴;

Из расчета видно, что , т.е. максимальный момент инерции возникает относительно оси v, которая ближе к оси z, оси с наибольшим значением момента инерции .

Сумма главных моментов инерции должна быть равна сумме осевых моментов инерции, или полярному моменту инерции

.

Определение главных моментов инерции и положения главных осей с помощью круга Мора (рис. 3).

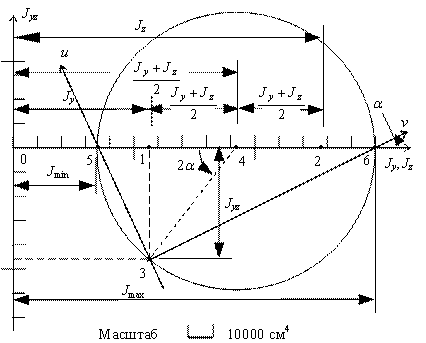
Рис.3

Определяем из чертежа в масштабе главные моменты инерции и угол поворота главных осей (с помощью транспортира):

см⁴; см⁴; .

Графический метод показал хорошее совпадение с результатами аналитического расчета.

Пример 13.

Для сечения, составленного из швеллера №20а, равнобокого уголка (80х80х8)×10^-9 м³ и полосы (180х10)×10^-6 м² (см. рис.) требуется:

1. Найти общую площадь сечения;

2. Определить центр тяжести составного сечения;

3. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих через его центр тяжести;

4. Найти положение главных центральных осей инерции;

5. Определить величины главных центральных моментов инерции сечения и проверить правильность их вычисления;

6. Вычислить величины главных радиусов инерции.

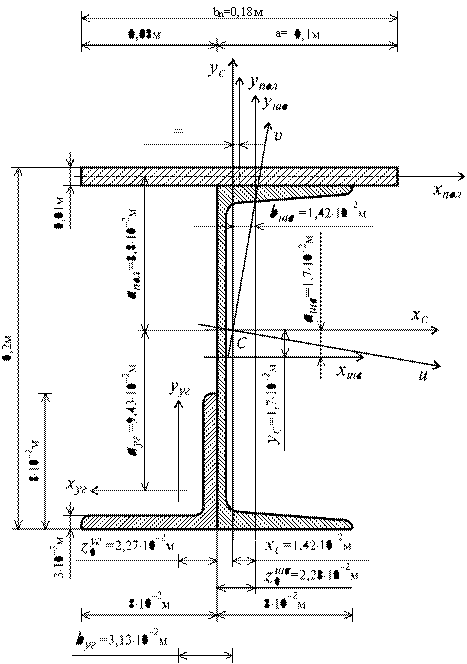
Решение.

1. Определение общей площади составного сечения. Общая площадь составного сечения определяется по формуле:

,     А = (25,2 + 12,3 + 18)×10^-4 = 55,5×10^-4 м².

2. Определить центр тяжести составного сечения. В качестве вспомогательных осей для определения положения центра тяжести примем горизонтальную и вертикальную оси x_шв и y_шв , проходящие через центр тяжести швеллера. Статические моменты площади всего сечения относительно этих осей будут равны:

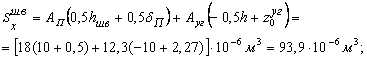
Координаты центра тяжести вычисляем по формулам:

м, м.

3. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих через его центр тяжести. Для определения указанных моментов инерции составного сечения воспользуемся формулами, выражающими зависимость между моментами инерции относительно параллельных осей:

(1)

(2)

(3)

В этих формулах расстояние между осями, проходящими через центр тяжести составного сечения, и осями, проходящими через центры тяжести каждой составной части фигуры, а и b (см. рис.), в рассматриваемом случае будут равны:

м, м;

м;

м.

Подставив числовые значения величин в формулы (1) и (2), получим:

= [1670 + 25,2×(-1,7)² + 73,4 + 12,3×(-9,43)² + 1,5 + 18×(8,8)²]×10^-8 = 4305,4×10^-8 м⁴.

= [139 + 25,2×(1,42)² + 73,4 + 12,3×(-3,13)² + 486 +18×(0,14)²]×10^-8 = 870,1×10^-8 м⁴.

При вычислении центробежного момента инерции составного сечения следует иметь в виду, что и равны 0, так как швеллер и полоса имеют оси симметрии, а

,

где - угол между осью x и главной осью уголка. Этот угол может быть положительным или отрицательным. В нашем примере  = +45°, поэтому:

м⁴.

Далее, подставив числовые значения в формулу (3), получим величину центробежного момента инерции составного сечения:

= [0 + 25,2 × (-1,7) × 1,42 + 42,85 + 12,3 × (-9,43) (-3,13) + 0 + 18 × 8,8 × 0,14] ×10^-8 = 367,2×10^-8 м⁴.

4. Найти положение главных центральных осей инерции. Угол наклона главных осей инерции, проходящих через центр тяжести составного сечения, к центральным осям инерции и определим по формуле:

.

Так как угол получился отрицательным, то для отыскания положения главной оси максимального момента инерции u следует ось , осевой момент инерции относительно которой имеет наибольшее значение, повернуть на угол по ходу часовой стрелки. Вторая ось минимального момента инерции v будет перпендикулярна оси u.

5. Определить величины главных центральных моментов инерции сечения и проверить правильность их вычисления. Величины главных центральных моментов инерции составного сечения вычисляем по формуле:

Для контроля правильности вычисления величины моментов инерции составного сечения производим проверки.

1-ая проверка: ;

I_max + I_min = (4344,55 + 830,95)×10^-8 = (5175,5)×10^-8 м⁴;

= (4305,4 + 870,1)×10^-8 = (5175,5)×10^-8 м⁴.

2-ая проверка: ;

4344,55 ×10^-8 > 4305,4×10^-8 > 870,1×10^-8 > 830,95×10^-8 м⁴.

Проверки удовлетворяются, что говорит о правильности вычисления моментов инерции составного сечения.

6. Вычислить величины главных радиусов инерции. Величины главных радиусов инерции вычисляем по известным формулам:

Пример 14.

Для составного сечения, состоящего из швеллера и уголка (рис.1) требуется:

1) определить положение центра тяжести;

2) найти величины осевых и центробежных моментов инерции относительно центральных осей;

3) определить направления главных центральных осей;

4) найти величины моментов инерции относительно главных нейтральных осей;

5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.

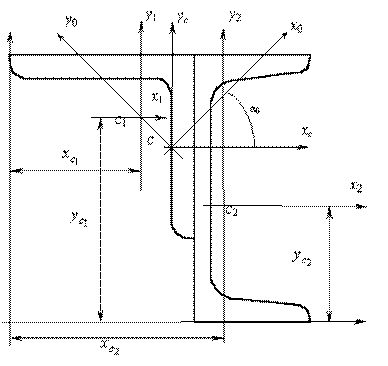
Рис.1

Решение.

Выпишем данные из сортамента.

Уголок равнобокий № 14 (10)

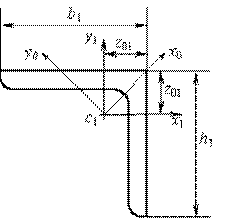
h₁ = b₁ = 14 cм, F₁ = 27,3 см²,

Z₀₁ = 3,82 см,

см⁴.

см⁴, см⁴.

см⁴.

 где угол взят отрицательным, так как ось х₀ для совпадения с осью х₁ поворачивается по часовой стрелке, .

Швеллер №20

h₂ = 20 см, b₂ = 7,6 см,

Z₀₁ = 2,07 см,

F₂ = 23,4 см², =1520 см⁴,

=87,8 см⁴, =0.

1. Определим положение центра тяжести составного сечения.

Для этого следует начертить профиль составного сечения в масштабе 1:2, провести координатные оси .

Выберем координатную систему х-у так, чтобы составной профиль оказался в первой четверти.

Координаты центра тяжести определим из выражений

, .

где S_х, S_у - статические моменты составного сечения относительно осей х и у.

; ;

см;

см;

см;

см;

см³;

см³;

см²;

см, см.

По координатам х_с и у_с найдем положение центра тяжести сечения. Через т.С проведем оси х_с-у_с - центральные оси.

2. Вычислим величины осевых и центробежных моментов сечения относительно центральных осей х_с -у_с:

;

;

.

где

см;

см;

см;

см;

см⁴;

см⁴;

см⁴.

3. Определим направление главных центральных осей.

Главные оси х₀ -у₀ проходят через центр тяжести т.С и повернуть относительно центральных осей на угол , определяемый из формулы

, , .

T.к. , то оси х₀ - у₀ получаются поворотом от осей х_с - у_с против часовой стрелки.

4. Найдем величины моментов инерции относительно главных центральных осей

см⁴.

см⁴.

При правильно выполненных вычислениях должно выполняться равенство

2513,26+1036,92=2835+715,18

.

Пример 15.

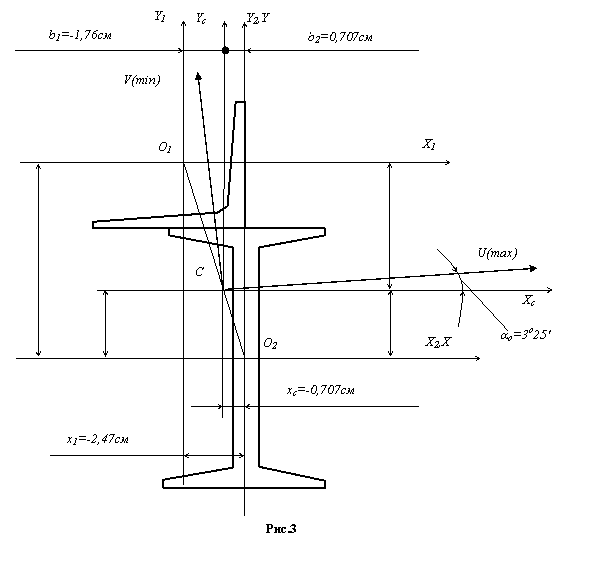
Найти положение главных центральных осей инерции и значение главных моментов инерции для сечения состоящего из равнобокого уголка и двутавра (см. рис.1). Вычертить сечение в масштабе 1:2 и указать на нём все размеры в числах и все оси, если дано: уголок 90х7, двутавр №22.

Решение.

Из сортамента выбираем необходимые данные.

Для уголка равнобокого 90х7 по ГОСТ 8509-89 b = 90 мм, d = 7 мм, z₀ = 2,47 см, F₁=12,28 см², I_x1 = I_y1 = 94,3 см⁴, I_max = 149,67 см⁴, I_min = 38,94 см⁴.

Для двутавра по ГОСТ 8239-89 h = 220 мм, b = 110 мм, d =5,7 мм, F₂ = 30,6 см², I_x2 = 2550 см⁴, I_Y2 = 157 см⁴.

1. Проводим вспомогательную систему осей координат (Х, Y). Начало координат целесообразно расположить в центре тяжести какой-либо из фигур, например двутавра (чтобы сократить объём вычислений). Определяем координаты центра тяжести С всей фигуры в системе осей Х и Y:

где

Через центр тяжести С (рисунок 3) проводим центральные оси Х_С и Y_C параллельно проведённым ранее собственным осям уголка и двутавра (Х₁, Y₁, Х₂, Y₂).

В системе координат центральных осей Х_С и Y_C координаты центров тяжести уголка и двутавра определяем из выражений

Данные сводим в таблицу 1.

Таблица 1

Точка	хi, см	yi, см	ai, см	bi, см
О1	- 2,47	13,47	9,61	- 1,76
О2	0	0	- 3,86	0,707

2. Вычисляем осевые и центробежный моменты инерции относительно центральных осей X_с, Y_с:

Для равнобокого уголка

Для двутавра

Знак центробежного момента инерции уголка определяем по следующему правилу (см. рис.2):

Рис.2

3. Находим угол наклона главных центральных осей U и V относительно центральных осей Х_С и Y_C:

Поскольку угол положительный, главная центральная ось U откладывается относительно оси Х_С против часовой стрелки, а так как I_xc >I_yc, то ось U является осью, относительно которой момент инерции будет максимальным.

4. Вычисляем главные моменты инерции

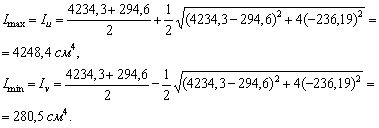
5. Проверка

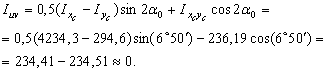
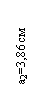
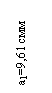
Онлайн-калькулятор "Расчет геометрических характеристик прямоугольного треугольника"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00