Главная

Лекция 4 (продолжение). Примеры решения задач по геометрическим характеристикам плоских сечений

Геометрические характеристики простых сечений

Пример 1.

Определить положение центра тяжести полукруга (см. рис.).

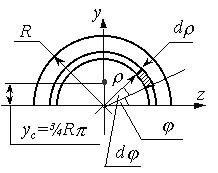
Решение.

Направим ось y по оси симметрии полукруга, а ось z совместим с его основанием. В этом случае z_c=0, надо определить только координату y_c. Подсчитаем S_z непосредственным интегрированием по площади полукруга:

.

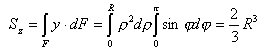Далее по формуле находим расстояние центра тяжести от основания полукруга:

.

Пример 2.

Для прямоугольного поперечного сечения определить моменты инерции относительно осей геометрической симметрии и осей, совпадающих со сторонами прямоугольника (см. рис.).

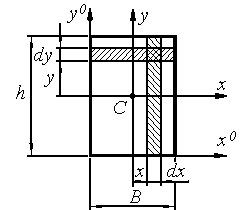
Решение.

Оси x, y являются главными центральными для прямоугольного поперечного сечения, так как они совпадают с осями геометрической симметрии. Оси x⁰, y⁰ − в данном случае будут вспомогательными. Для определения осевого момента инерции J_x выделим на расстоянии y полоску шириной B и толщиной dy, следовательно dF=Bdy, тогда

Теперь рассмотрим на расстоянии x от оси y полоску шириной h и толщиной dx, в этом случае dF=hdy и момент инерции J_y будет равен

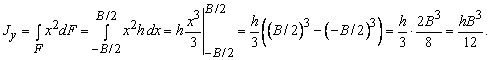
Центробежный момент инерции

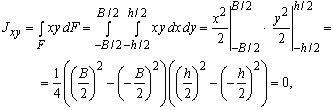
где .

Моменты инерции относительно осей x⁰, y⁰, можно вычислить используя формулы переноса, полагая , тогда

Пример 3.

Определить геометрические характеристики относительно центральных и главных осей для сечения в виде прямоугольного треугольника, изображенного на рисунке.

Решение.

Отнесем треугольник к вспомогательной системе координат x⁰, y⁰. В качестве элементарной площади возьмем полоску на расстоянии y⁰ толщиной dy⁰ и переменной ширины b(y⁰) так, что

.

Из подобия треугольников нетрудно установить, что:

,

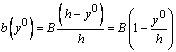тогда .

Статический момент будет равен

По аналогии получим

Площадь треугольника

.

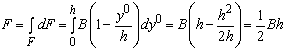Координаты центра тяжести C определим по формулам:

Через точку C проводим центральные оси x, y параллельные осям

Момент инерции и аналогично равны:

,

.

Для определения момента инерции относительно центральной оси x воспользуемся формулой при параллельном переносе осей

.

Так как , то

Центробежный момент

,

где ; .

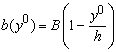Интегрируя, получаем

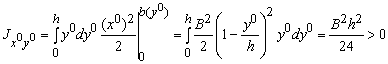
Перейдя к центральным осям x и y, получим

.

Определение направлений главных осей:

.

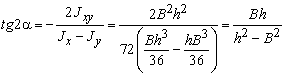Проводим главные центральные оси 1 и 2.

Если, например, , то имеем равнобедренный треугольник, для которого , , . Тогда:

.

Пример 4.

Определить площадь и моменты инерции относительно главных центральных осей инерции круглого поперечного сечения диаметра (см. рис.).

Решение.

Выберем оси x, y, которые для круглого сечения будут главными и центральными, так как являются осями геометрической симметрии. В качестве элементарной площади dF возьмем полоску на уровне y толщиной dy и шириной b(y), т.е. . Координаты точки A на контуре сечения, а также dy, b(y) равны:

.

Тогда элементарная площадь

.

Площадь круга

.

Моменты инерции относительно оси x

Такое значение имеет момент инерции относительно оси y. Следовательно, полярный момент инерции для круга

.

Пример 5.

Определить положение центра тяжести и моменты инерции относительно главных центральных осей для поперечного сечения в виде полукруга (см. рис.).

Решение.

Проводим вспомогательные оси x⁰, y⁰ при этом учтем, что ось y⁰ является осью геометрической симметрии и будет одной из главных центральных осей инерции сечения − 1 (см. рис.). Вторая главная центральная ось будет проходить через центр тяжести сечения и перпендикулярно оси y⁰.

Площадь полукруга .

Статический момент относительно вспомогательной оси x⁰ равен

,

где .

Координаты центра тяжести в осях x⁰, y⁰:

Через точку С с координатами , проводим вторую главную центральную ось инерции − 2 (см. рис.). Таким образом? положение главных центральных осей для заданного сечения − определено.

Моменты инерции полукруга относительно осей x⁰, y⁰ будут равны половине моментов инерции полного круга, найденных в предыдущей задаче:

.

Определим осевые моменты инерции сечения относительно главных центральных осей

Пример 6.

Найти центробежный момент инерции для равнобокого уголка 125х125х10 (мм) относительно центральных осей x, y.

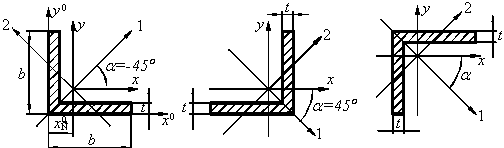
а) б) в)

Решение.

Из таблицы ГОСТа для уголка (рис. а) находим

J₁=571 мм⁴, J₂=149 мм⁴, J₁₂=0, =3,45 мм, =-45⁰, F=24,3 мм².

Центробежный момент

мм⁴.

Для уголка (рис. б) угол ,

мм⁴.

Для уголка (рис. в) угол ,

J_xy=211 мм⁴.

Пример 7.

Определить центробежный момент инерции неравнобокого уголка 160х100х10 относительно центральных осей, параллельных полкам (см. рис.).

Решение:

По таблице сортамента прокатной стали в соответствии с ГОСТ 8510-72 (СТ СЭВ 255-76) имеем = 204 cм⁴, = 667 cм⁴, I_{u min} = 121 cм⁴, = 0,390.

Для определения центробежного момента инерции воспользуемся формулами поворота осей (переход от главных осей к данным )

.

Угол в данном случае отрицателен, так как кратчайшее совмещение оси с происходит по часовой стрелке. Главный момент инерции задан в таблице сортамента, а главный момент определяем из соотношения

,

откуда = 204 + 667 – 121 = 750 см⁴.

Таким образом, центробежный момент уголка будет равен

= 0,5(121-750)×(-0,677) = 213 см⁴.

Пример 8.

Определить центробежный момент инерции равнобокого уголка 100х100х10 относительно центральных осей, параллельных полкам (см. рис.).

Решение:

По таблице сортамента прокатной стали в соответствии с ГОСТ 8509-72 (СТ СЭВ 104-74) имеем =284 см⁴, =74,1 см⁴, =3,84 см, =1,96 см.

Пользуясь формулой поворота, находим

,

см⁴.

Пример 9.

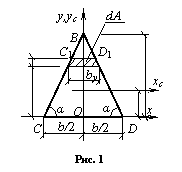
Определить центр тяжести треугольного поперечного сечения, показанного на рисунке.

Решение.

Поперечное сечение представляет собой равнобедренный треугольник, а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного сечения лежит на этой оси.

Для нахождения центра тяжести используем формулу Запишем

(а)

Из подобия треугольников и находим

или откуда

Найденное значение b_y подставляем в формулу (а) для вычисления статического момента S_x:

В этом случае формула дает

На рисунке проводим линию у = у_с = h/3. Центр тяжести треугольного поперечного сечения будет лежать на пересечении проведенной линии и оси у. Координаты центра тяжести этого сечения: х = 0, у = h/3.

Ответ: x_c = 0, y_c = 4R/(3).

Пример 10.

Определить статические моменты S_x и S_y сложного поперечного сечения (см. рис.). Найти координаты его центра тяжести.

Решение.

Разбиваем сложное поперечное сечение на две простые фигуры: прямоугольное сечение с размерами и площадью A₁ = h²/2, координаты центра тяжести (C₁) которого y_1c = h/2, x_1c = h/4 и прямоугольное сечение с центром тяжести С₂ (y_2c = h/2, x_2c = 5h/16) и площадью A₂ = 9h²/32.

По формулам

вычисляем статические моменты всего сечения:

Площадь поперечного сечения всей конструкции А находим как разность площадей А₁ и А₂: А = А₁ – А₂ = 7h²/32. Подставляя полученные значения в формулы , находим координаты центра тяжести С всего сечения:

y_c = S_x/A = h/2; x_c = S_y/A = 19h/112.

Пример 11.

Определить полярный момент инерции круглого поперечного сечения (см. рис.) относительно точки С.

Решение.

За элементарную площадку выберем кольцевую область вокруг центра С с внутренним радиусом ρ и шириной dρ. Определим площадь элементарной площадки . Затем результат подставляем в формулу :

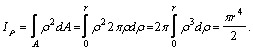
Пример 12.

Определить осевые моменты инерции круглого сплошного поперечного сечения относительно произвольных центральных осей х, у (см. рис.).

Решение.

В примере 17 найдено, что . Однако для круглого сплошного сечения I_x = I_y, поэтому формула для этого сечения принимает вид: 2I_x = I_ρ, откуда находим

Пример 13.

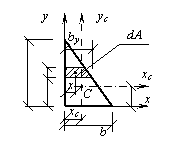
Определить осевые моменты инерции I_x, I_y прямоугольного треугольника относительно случайных осей х, у (см. рис.). Вычислить положение центра тяжести. Найти значения осевых моментов инерции ,и центробежный момент инерции относительно центральных осей х_с, у_с, проходящих через центр тяжести С. Определить расположение главных осей инерции поперечного сечения в форме сплошного прямоугольного треугольника.

Указания. Для нахождения центробежного момента инерции можно использовать формулы и которые для рассматриваемого случая принимают вид:

Из подобия треугольников находим (см. рис.): откуда следовательно, площадь элементарной площадки dA будет

Горизонтальная координата х центра тяжести элементарной площадки dA определяется как x = b_y /2 =b (h – y)/(2h).

Подставим значения х и dA в формулу для определения I_xy:

Переходим к центральным осям х_с и у_с, для которых

Ответ:

Пример 14.

Определить расстояние а между элементами пакета, состоящего из трех досок размером , при условии равенства главных моментов инерции относительно осей х и у (см. рис.).

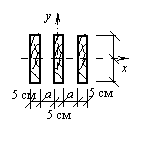
Решение.

Момент инерции всего сечения относительно оси х будет

При определении момента инерции сечения относительно оси у для двух крайних прямоугольников следует воспользоваться формулой так как ось у не является для них центральной и, следовательно, для всего пакета из трех досок будем иметь

По условию задачи I_x = I_y, или 17280 = 240a² + 2400a + 6750.

Решив полученное квадратное уравнение, найдем a = 3,3 см.

Пример 15.

Сечение стержня представляющее собой фигуру, обладающую одной осью симметрии, показано на рис. 1. Требуется найти моменты инерции этой фигуры относительно главных центральных осей.

Рис.1

Решение.

Ось – ось симметрии фигуры (рис. 1) является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату по формуле . Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I , III и прямоугольник II (см. рис. 2). Площадь фигуры

Для определения статического момента выберем вспомогательную ось , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе :

Тогда по

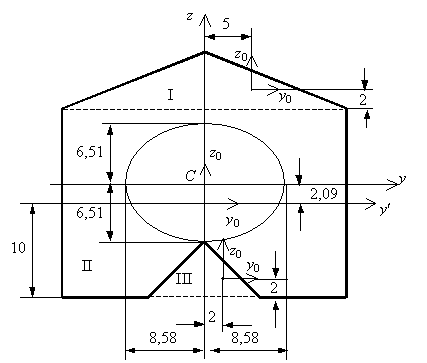
Рис.2

Откладываем эту координату и проводим через центр тяжести (точку С на рис. 2) главную центральную ось .

Найдем моменты инерции всей фигуры относительно осей и , складывая (или вычитая) моменты инерции составляющих фигур:

;

.

Для определения момента инерции каждой из фигур I, II и Ш используем формулы изменения моментов инерций при параллельном переносе осей , . Моменты инерции прямоугольника II находим по формулам ; ; и треугольников I и Ш находим по формулам ; ; относительно собственных центральных осей (см. рис. 2).

Тогда

В заключение вычислим радиусы инерции относительно главных центральных осей по формулам , и построим эллипс инерции.

Эллипс инерции показан на рис. 2.

Пример 16.

Для фигуры, показанной на рисунке определить главные моменты инерции и положение главных осей инерции.

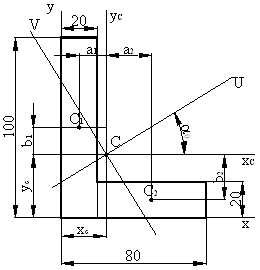
Решение.

Разбиваем сложное сечение на простейшие геометрические фигуры

S₁ = 2000 мм², S₂ =1200 мм², S = 3200 мм².

Выбираем произвольные оси XOY.

Определяем положение центра тяжести сечения

Определяем статические моменты площади

мм³

мм³

Находим координаты центра тяжести

мм;

мм.

Проводим центральные оси X_cOY_c

мм,

мм,

мм,

мм.

Вычисляем моменты инерции Ix_c, Iy_c

мм⁴

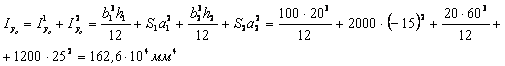
6) Вычисляем центробежный момент инерции Ix_cy_c

Определяем положение главных осей инерции

Если I_x>I_y и , то угол откладывается от оси Х_с против часовой стрелки.

7) Вычисляем главные моменты инерции I_max, I_min

Пример 17.

Определить положение центра тяжести сечения, приведенного на рис.1 (размеры даны в см).

Решение:

Разбиваем сечение на три прямоугольника и выбираем вспомогательные оси uv (рис. 2).

Рис.1

Вычисления представим в виде следующей таблицы

Номер вычисления	Координаты, см		Площадь Аi, см^2	Статические моменты, см^3
	ui	vi		uiAi	viAi
1 2 3	11 9 5	1 8 15	12 24 20	132 216 100	12 192 300
			56	448	504

Рис.2

Определяем координаты центра тяжести сечения:

см,

см.

Пример 18.

Для данного сечения определить моменты инерции относительно центральных осей x и y.

Решение:

Моменты инерции прямоугольников относительно собственных центральных осей определяем по формулам , . Пользуясь формулами перехода к параллельным осям, вычисляем искомые моменты инерции, представленные в нижеприведенной таблице.

Номер элемента	Координаты центра тяжести, см		Площадь Аi, см^2	Моменты инерции площадей, см^4
	xi	yi				Ixi			Iyi		xiyiAi	Ixiyi
1	3	-8	12	4	768	772	36	108	144	0	-288	-288
2	1	-1	24	288	24	312	8	24	32	0	024	-24
3	-3	6	20	6,7	720	727	167	180	347	0	-360	-360
				299	1512	1811	211	312	523	0	-672	-672

Онлайн-калькулятор "Расчет геометрических характеристик прямоугольника"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00