Главная

Лекция 9 (продолжение). Примеры решения по устойчивости сжатых стержней

Подбор сечения центрально-сжатого стержня из условия устойчивости

Пример 1.

Стержень, показанный на рис. а сжимается силой F = 600 кН. Сечение стержня, состоящее из двух равнобоких уголков, изображено на рис. б. Материал стержня – сталь С235 с допускаемым напряжением Требуется подобрать размеры уголков так, чтобы выполнялись условия устойчивости и прочности и расход материала был минимальным. Ослабления составляют 15% площади сечения.

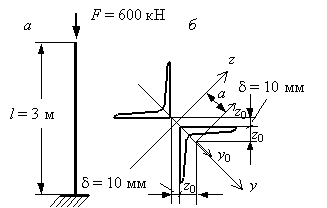
Решение.

Сечение стержня состоит из уголков (прокатного профиля), поэтому используем для подбора сечения метод последовательных попыток. Поскольку в условии устойчивости имеем сразу две неизвестные величины ( и ), то одной из них задаемся произвольно. Удобно задаться . Тогда из условия устойчивости найдем

Площадь одного уголка Из сортамента прокатной стали выбираем уголок, удовлетворяющий этому условию. Отметим, что в сортаменте может быть несколько уголков с примерно одинаковой площадью: уголки с длинной полкой и тонкой стенкой и уголки с короткой, но более толстой стенкой. Выбирать следует самые тонкие уголки, т.к. при одинаковой площади радиус инерции у тонких уголков больше и, следовательно, гибкость стержня с сечением из тонкого уголка меньше, а чем меньше гибкость, тем более устойчив стержень. В рассматриваемом примере выберем уголок 180х11, площадь которого . Найдем радиусы инерции относительно главных центральных осей y и z, которыми являются оси симметрии сечения (см. рис. б). Следует ожидать, что радиус инерции относительно оси y будет минимальным, так как материал ближе расположен к оси y, чем к оси z. Убедимся в этом.

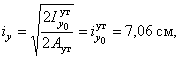
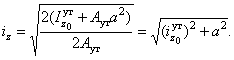
Радиус инерции одного уголка относительно оси берем из сортамента: , а расстояние а (см. рис. б) сосчитаем:

Таким образом, очевидно, что

и

Теперь найдем гибкость стержня (заметим, что, если в сортаменте выбрать уголок с более толстой полкой, но с примерно такой же площадью, например, уголок 160´12 (А_уг = 37,4 см²), минимальный радиус инерции сечения из двух таких уголков будет i_min = 6,23 см и гибкость стержня будет на 13% больше, чем для уголка 180´11).

и из таблицы, интерполируя, найдем . Проверим условие устойчивости

Условие устойчивости выполняется, но сечение не является экономичным. Поэтому сделаем еще попытку. Уменьшим размеры сечения и примем самый тонкий уголок их тех, у которых длина полки 160 мм, а именно, уголок 160´10. , и гибкость стержня

По таблице (справочные данные) находим и условие устойчивости выполняется с небольшим запасом:

Сечение из двух уголков 160´10 можно считать экономичным. Условие прочности для подобранного сечения тоже выполняется, поскольку согласно условию .

В заключение найдем действительный коэффициент запаса устойчивости. Поскольку стержень с подобранным сечением из уголков 160х10 имеет гибкость , находящуюся в пределах между и , то определяем критическую силу по формуле Ясинского

Действительный коэффициент запаса устойчивости

Пример 2.

Стальной стержень длиной сжимается силой .

Требуется:

1. Найти размеры поперечного сечения при с помощью метода последовательных приближений;

2. Найти значение критической силы и коэффициент запаса устойчивости.

Решение.

1) В условии устойчивости

неизвестны величины и А.

В первом приближении

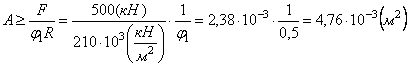
С другой стороны

. Следовательно,

Определим минимальный радиус инерции

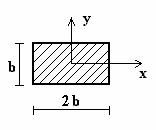
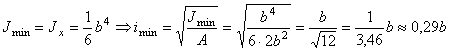
Коэффициент приведения длины , согласно для данного типа закрепления равен 0,5.

Гибкость стержня

По таблице из справочника (коэффициенты продольного изгиба центрально сжатых элементов по СНиП II 23 – 81) (справочные данные) находим

при

при

при

Интерполяцией определяем

Сравниваем

Проверка:

Считаем напряжения

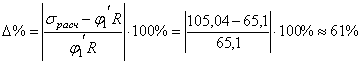
61% > 5%

Во втором приближении принимаем

при

при

Сравниваем

Проверка:

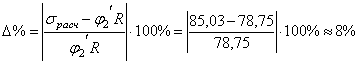
8% > 5%

В третьем приближении

при

при

Сравниваем

Проверка:

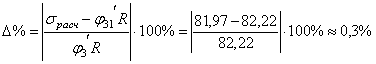
0,3% < 5%

Полученное значение близко к принятому, поэтому окончательно

2) Найдем значение критической силы и коэффициент запаса устойчивости.

Поскольку гибкость , а для малоуглеродистой стали предельная гибкость , то в нашем случае

,

значит применима формула Эйлера.

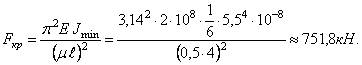
Коэффициент запаса устойчивости

Пример 3.

Подобрать размер поперечного сечения квадратной стойки показанной на рисунке (для данной стойки ). Стойка нагружена сжимающей силой кН, длина стойки м, материал стойки – сталь 3. Определить критическое напряжение, критическую силу и запас устойчивости как отношение критической силы к заданной. Допускаемое напряжение на сжатие МПа.

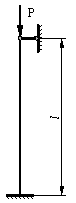
Решение.

Используя условие устойчивости и метод последовательных приближений, определим размеры поперечного сечения квадратной стойки.

Первое приближение.

Принимаем . Тогда

Для квадратного сечения имеем: , тогда см.

Найдём фактическое значение гибкости стержня и коэффициента уменьшения основного допускаемого напряжения.

Для этого находим:

минимальное значение осевого момента инерции ;

минимальное значение радиуса инерции ;

фактическая гибкость стойки .

Подставив числовые значения, получим

, .

Используя данные таблицы 2 путём линейной интерполяции определяем фактическое значение коэффициента :

.

Поскольку найденное фактическое значение коэффициента значительно отличается от принятого значения , то вычисления продолжаем дальше.

Второе приближение.

На втором приближении принимаем:

.

Тогда находим:

.

см, см, .

.

Фактическое значение коэффициента ещё сильно отличается от принятого значения коэффициента на втором приближении . Поэтому вычисления повторяем ещё.

Третье приближение.

На третьем приближении принимаем:

.

Тогда находим:

.

см, см, .

.

Проверим прочность подобранной стойки.

Фактическое напряжение в сжатой стойке:

МПа.

Допускаемое напряжение для сжатой стойки на устойчивость:

МПа.

Перенапряжение составляет:

,

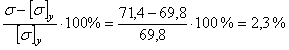что допустимо.

Окончательно принимаем 2,37 см, 5,6 см².

Определим критическое напряжение и критическую силу для спроектированной стойки.

Поскольку гибкость стойки в нашем случае , следовательно, для определения критической силы используем формулу Эйлера:

МПа.

Тогда критическое значение силы

кН.

Определим значение коэффициента запаса устойчивости:

.

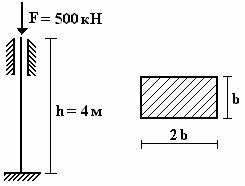
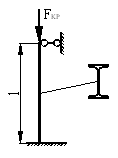
Пример 4.

Подобрать сечение двутаврового стержня, если длина стержня l = 4 м, сжимающая сила F = 500 кН, допускаемые напряжения на сжатие = 150 МПа.

Решение.

Принимаем первоначальный коэффициент снижения допускаемого напряжения = 0,5. Тогда допускаемое напряжение на устойчивость:

.

Определяем необходимую площадь поперечного сечения стержня:

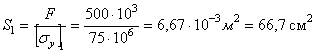
По таблицам сортамента подбираем двутавр № 40: S = 72,6 см², i_min = i_y = 3,03 см.

Находим гибкость стержня. По условию задачи коэффициент = 0,7.

По известной гибкости стержня определяем из таблицы для коэффициентов (справочные данные) коэффициент .

= 0,6684

Определяем допускаемое напряжение на устойчивость:

.

Определяем рабочее напряжение стержня:

Сравним рабочее и допускаемое напряжение на устойчивость:

- недонапряжение

При расчетах на устойчивость отклонение от допускаемого напряжения не должно превышать 5%, поэтому подобранное сечение слишком велико, и необходимо продолжить подбор сечения, используя метод последовательного приближения.

Определяем из двух величин напряжений среднее напряжение:

Определяем необходимую площадь поперечного сечения стержня:

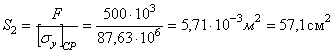
По таблицам сортамента подбираем двутавр № 36: S = 61,9 см², i_min = i_y = 2,89 см.

Находим гибкость стержня:

Определяем коэффициент :

= 0,6279

Определяем допускаемое напряжение на устойчивость:

.

Определяем рабочее напряжение стержня:

Сравним рабочее и допускаемое напряжение на устойчивость:

- недонапряжение

Подобранное сечение слишком велико, и необходимо продолжить подбор сечения.

Определяем из двух величин напряжений среднее напряжение:

Определяем необходимую площадь поперечного сечения стержня:

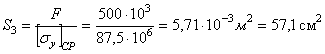
Среднее напряжение и площадь поперечного сечения стержня по сравнению с предыдущим приближением изменилась незначительно. Поэтому, выбирая по таблицам сортамента сечение стержня, мы снова получим двутавр №36. Но так как, по этому двутавру расчет уже производился, то примем двутавр № 33 и подсчитаем величину перенапряжения в стержне. Если перенапряжение не превысит 5%, то окончательно примем двутавр № 33.

По таблицам сортамента для двутавра № 33: S = 53,8 см², i_min = i_y =2,79см.

Находим гибкость стержня:

.

Определяем коэффициент :

= 0,5968.

Определяем допускаемое напряжение на устойчивость:

.

Определяем рабочее напряжение стержня:

.

Сравним рабочее и допускаемое напряжение на устойчивость:

Перенапряжение стержня составило менее, чем 5%, поэтому окончательно принимаем двутавр № 33.

Пример 5.

Подобрать двутавровое сечение стойки с одним защемленным концом (см. рис.), сжатой силами Р = 400 кН; длина стойки l=1,5 м. Основное допускаемое напряжение =160 МПа.

Решение.

Так как в условии устойчивости нам не известно ни , ни , одной из этих величин необходимо задаться. Примем для первого приближения =0,5. В этом случае необходимая площадь поперечного сечения стержня будет равна

или

По сортаменту выбираем двутавр №24b с площадью F=52,6 см². Наименьший радиус инерции сечения. Соответствующая гибкость стойки

Коэффициент по интерполяции между значениями его из таблицы для =120 и =130 равен =0,43.

Расчетным напряжением будет:

Перенапряжение составляет . Подбираем двутавр №27, ;; наибольшая его гибкость. Так как коэффициент =0,45, то расчетное напряжение

Перенапряжение составляет теперь что допустимо.

Пример 6.

Подобрать двутавровое сечение сжатого стержня с шарнирным закреплением концов, если сжимающая сила P=500 кН, длина стержня 2 м. Основное допускаемое напряжение 160 МПа.

Решение.

Принимая в качестве первого приближения =0,5, получаем

Из таблиц сортамента (ГОСТ 8239-72) выбираем двутавр №36, у которого F=61,9 см².

Наименьший радиус инерции из тех же таблиц сортамента i_min=2,89 см. Гибкость стержня

Коэффициент по таблице (справочные данные) для стали СтЗ при =70 равен .

Разница между и значительная, поэтому повторим расчет, принимая

Тогда

Принимаем двутавр №30, у которого F=46,5 см², i_min=2,69 см. Гибкость стержня

Коэффициент из таблицы (справочные данные) (интерполируя значения, соответствующие =70 и 80) получаем равным =0,78.

Напряжение в поперечном сечении стержня получается при этом

Допускаемое же напряжение при расчете на устойчивость

Недонапряжение составляет .

Делаем еще одну попытку. Примем . Получим

Принимаем двутавр №27, у которого F=40,2 см², i_min=2,54 см. Получим гибкость стержня .

Из таблиц коэффициент =0,75.

Напряжение

Допускаемое напряжение

Перенапряжение , что допустимо.

Пример 7.

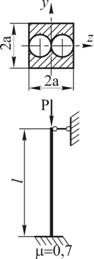
Стальной стержень длиной сжимается силой . Определить размеры поперечного сечения, показанного на рис. 1, при допускаемом напряжении на простое сжатие . Способ крепления стержня показан на рисунке.

Решение.

В расчетной формуле на устойчивость , имеются две неизвестные величины – коэффициент уменьшения допускаемого напряжения и искомая площадь поперечного сечения . Поэтому при подборе сечений приходится пользоваться методом последовательных приближений. Первоначально задаются коэффициентом уменьшения допускаемого напряжения и определяют требуемую площадь поперечного сечения. Далее определяют гибкость стержня и соответствующий ей коэффициент уменьшения допускаемого напряжения, который определяется по таблице (справочные данные). При отличии фактического от первоначально принятого, проводят следующее приближение, принимая следующего приближения, как среднее по величине значение между первоначально принятым и фактически определенным.

При подборе сечения последовательным приближением, возможно, придется несколько раз определять минимальный радиус инерции. Упростим вычисления, выражая минимальный радиус инерции через площадь поперечного сечения.

Площадь сечения определим как сумму площади квадрата и отрицательной площади двух круглых отверстий

;

;

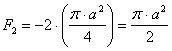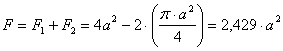
Минимальный радиус инерции определяются по формуле .

Координатные оси и являются главными центральными осями инерции составного сечения, так как центральная ось является осью симметрии составного сечения. Определим осевой момент инерции как разницу осевого момента инерции квадрата и двух круглых отверстий относительно осей и .

Ось является главной центральной осью, как для квадрата, так и двух круглых отверстий. Осевой момент инерции квадрата относительно осей и будет равен:

Осевой момент двух круглых отверстий относительно оси :

Относительно оси осевой момент круглых отверстий определим как осевой момент относительно оси, параллельной главной центральной оси.

где - осевой момент инерции одного круглого отверстия относительно его главной центральной оси инерции .

- расстояние между параллельными осями и .

- площадь одного круглого отверстия.

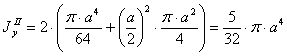
Осевой момент составного сечения относительно оси :

Осевой момент составного сечения относительно оси :

Минимальный осевой момент инерции

Радиус инерции

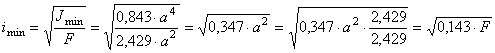
Выполняем первое приближение. Принимаем

Гибкость стержня

Из таблицы (справочные данные) для полученной гибкости определяем коэффициент уменьшения допускаемого напряжения.

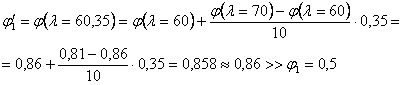
Перейдем ко второму приближению

Необходимая площадь поперечного сечения

Коэффициент уменьшения допускаемого напряжения.

Принимаем для третьего приближения

Коэффициент уменьшения допускаемого напряжения.

Вычисляем напряжение

Окончательно принимаем

,

При выполнении задания, в некоторых случаях, может быть получена гибкость, значение которой превышает 200.

В данных случаях определяют следующим образом.

Очевидно, что данная гибкость позволяет применять как формулу Эйлера, так и гиперболическую зависимость критического напряжения от гибкости (гиперболу Эйлера)

Допускаемое напряжение на устойчивость

,

где - коэффициент запаса устойчивости; для сталей - , причем, чем больше , тем меньше . Принимаем .

Допускаемое напряжение через коэффициент выражено как

Учитывая выше сказанное, можно записать

или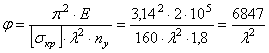

Подставляя значение гибкости в зависимость

,

определяется фактический коэффициент уменьшения допускаемого напряжения.

Пример 8.

Деревянная стойка длиной l = 4 м квадратного поперечного сечения сжимается силой F = 100 кН (см. рис.). Требуется подобрать размер стороны квадрата а так, чтобы выполнялись условия устойчивости и прочности и расход материала был минимальным. Ослабления составляют 15% площади сечения. Примем допускаемое напряжение на сжатие для дерева

Решение.

Поскольку размеры сечения могут быть любыми, используем метод последовательных приближений. Выполним первое приближение. Примем . Из условия устойчивости найдем площадь сечения, подставив :

.

Поскольку , то . Найдем минимальный радиус инерции сечения. Для квадрата любая ось является главной и радиус инерции относительно любой оси

.

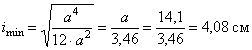Зная радиус инерции, вычислим гибкость стержня по формуле

.

По таблице (справочные данные) находим для дерева . Полученное значение еще сильно отличатся от величины , принятой в начале первого приближения, поэтому выполним второе приближение. Найдем как среднее арифметическое между и :

и повторим все действия, выполненные в первом приближении.

Этой гибкости соответствует .

Выполним еще одно, третье приближение.

Соответствующее этой гибкости значение отличается от на 1,2 %. Такая точность достаточна, поэтому примем . Для этого размера в условии устойчивости

достигнуто желаемое равенство.

В заключение проверим условие прочности, считая .

.

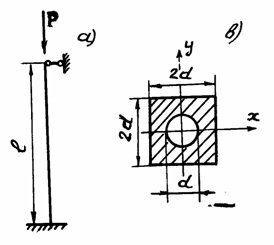
Пример 9.

Стальной стержень длиной l =3 м сжимается силой F =500 кН (см. рис.).

Требуется:

1) найти размеры поперечного сечения при допускаемом напряжении на простое сжатие = 160 МПа;

2) найти критическую силу и коэффициент запаса устойчивости.

Решение.

Из формулы имеем:

.

Так как здесь ни площадь F, ни коэффициент снижения допускаемого напряжения неизвестны, то расчет будем вести методом последовательного приближения.

В первом приближении, зная, что коэффициент принимает значения от нуля до единицы, зададимся значением =0,5. Чтобы на каждом этапе проводить меньше рутинной работы, выразим гибкость стойки через площадь сечения А, т.е.

, .

Минимальный момент инерции:

.

Площадь поперечного сечения составного сечения

.

Откуда

.

Минимальный радиус инерции:

.

Тогда для гибкости стойки получим формулу

.

Первое приближение. = 0,5. Определим площадь поперечного сечения:

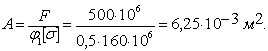
Определяем гибкость стойки:

Обратимся к любому справочнику сопротивление материалов и уточним значение коэффициента (обозначим его ) в соответствии с полученной гибкостью =72,5. Так как точно для этой гибкости значения коэффициента нет, определим его, воспользовавшись правилом линейного интерполирования. Делается это следующим образом: выпишем значения коэффициентов для сталей Ст.1, Ст.2, Ст.3, Ст.4, соответствующих гибкостям =70 и =80:

Замечаем, что при изменении на 10 единиц значение изменилось на 0,06. Наша же гибкость отличается от = 70 на 2,5 единицы. Какое изменение приходится на эти 2,5 единицы, мы не знаем и обозначим через x.

70	0,81
80	0,75

Итак, составляем пропорцию 10:2,5 = 0,06:х.

Отсюда:

.

Таким образом, при изменении на 2,5 единицы изменяется на 0,02. Тогда =0,81–0,02=0,79.

Сравниваем и

.

Допускается расхождение не более, чем на 5%; у нас же значительно больше 5%, поэтому переходим ко второму приближению:

Второе приближение. Определим площадь поперечного сечения

Определяем гибкость стойки

Обращаемся справочнику и уточняем значение . Действуем точно так же, как на первом этапе приближения.

,

.

Сравним и

Переходим к третьему приближению.

Третье приближение. Определим площадь поперечного сечения

Определяем гибкость стойки

Обращаемся к справочнику и уточняем значение .

,

.

Сравним и :

Отличие в пределах допустимого.

Принимаем стойку площадью А = 4,46×10^-3 м². Размер d этой стойки определим из формулы:

а гибкость = 85,6.

Определим величину критической силы.

Предельная гибкость для стали . Таким образом, гибкость нашей стойки =85,6 меньше предельной, и следовательно, критическую силу надо определять по формуле Ясинского:

кН.

Определим коэффициент запаса устойчивости на основании формулы:

Пример 10.

Исходные данные.

, , R =160 МПа, МПа, ( – коэффициент приведенной длины стержня, зависящий от характера закрепления его концов).

Требуется:

1. Найти размеры поперечного сечения стержня при расчетном сопротивлении стали R =160 МПа, пользуясь методом последовательных приближений.

2. Определить величину критической силы, если предельная гибкость равна .

3. Вычислить коэффициент запаса устойчивости.

Решение.

1. Размеры поперечного сечения стержня определим исходя из условия устойчивости

,

тогда,

где - коэффициент снижения расчетного сопротивления материала при продольном изгибе.

В расчётной формуле имеются две неизвестные величины – коэффициент и искомая площадь A. Поэтому при подборе сечения необходимо использовать метод последовательных приближений.

Для упрощения расчётов выразим геометрические характеристики сечения через модуль его размеров d.

Минимальный момент инерции (потеря устойчивости происходит в плоскости наименьшей жёсткости) определяется следующим образом:

.

Площадь поперечного сечения:

,

отсюда .

Минимальный радиус инерции:

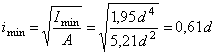
Приближение 1. В первом приближении коэффициент продольного изгиба обычно принимают , тогда

.

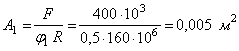Тогда:

,

.

Расчётная гибкость колонны:

.

Определяем значение коэффициента , соответствующего гибкости .

Путём линейной интерполяции:

.

Проверим выполнение условия устойчивости в первом приближении.

.

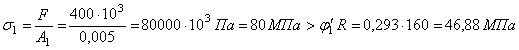Перенапряжение составляет:

,

что недопустимо. Следовательно, необходимо уточнение требуемых размеров сечения.

Приближение 2. Для ускорения процесса подбора за новое значение коэффициента принимаем среднее арифметическое первых двух

.

Тогда площадь сечения:

.

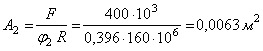Диаметр: ,

радиус инерции: .

Гибкость колонны:

.

Определяем значение коэффициента , соответствующего этой гибкости:

.

Проверим выполнение условия устойчивости. Рабочие напряжения

.

Расчётное сопротивление, гарантирующее устойчивость прямолинейной формы равновесия

.

В этом случае перенапряжение составляет:

,

что опять недопустимо, так как перенапряжение превышает 5%. Следовательно, необходимо третье приближение.

Приближение 3. В третьем приближении коэффициент продольного изгиба:

,

после чего повторяем расчётный цикл.

Площадь сечения:

.

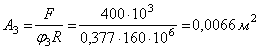Диаметр: ;

радиус инерции: .

Гибкость колонны:

.

Определяем значение коэффициента , соответствующего этой гибкости:

.

Рабочие напряжения третьего приближения:

.

Расчётное сопротивление при расчёте на устойчивость

.

.

Перенапряжение материала составляет:

.

что допустимо. Окончательно принимаем:

следовательно, сечение имеет размеры 72х108 см,

,

.

2. Находим величину критической силы.

Так как , то есть , то используем формулу Эйлера для определения критической силы:

.

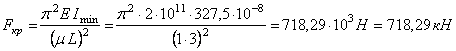3. Коэффициент запаса устойчивости.

.

Пример 11.

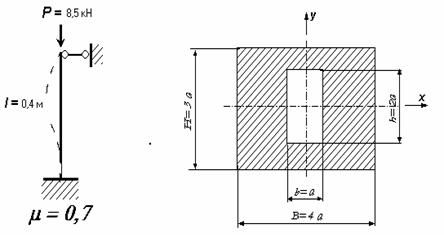
Пусть стальная стойка высотой l=0,4 м сжимается силой P = 8,50 кН. Требуется подобрать коробчатое поперечное сечение с характерным размером a (см. рис.).

Решение.

1. Определим моменты инерции сечения относительно координатных осей x и y . Очевидно, что

, .

Подставляя в эти выражения значения B, H, b и h, получим следующие формулы:

Легко видеть, что I_x < I_y , следовательно, сечение потерявшего устойчивость стержня будут поворачиваться вокруг оси X, при этом определяющим при расчете гибкости стойки окажется

окончательно получим

.

2. Определим гибкость первого приближения

3. При первоначальном назначении размера a следует руководствоваться опытом или интуицией. Из соображений здравого смысла зададимся величиной a = 0,005 м. Тогда значение гибкости первого приближения будет равно = 61,343. Воспользуемся таблицей коэффициентов снижения допускаемого напряжения (справочные данные) и выберем в качестве материала стойки Сталь 5. Будем иметь следующие исходные значения для проведения линейной интерполяции:

при = 60 = 0,80

при = 70 = 0,74.

С учетом этих данных для = 61,343 получим:

4. Определенное нами значение подставим в выражение и выясним, удовлетворяется ли неравенство. Имеем:

что подтверждает наличие устойчивого деформирования и отсутствие потери устойчивости при заданных размерах. Однако существенная недогрузка стойки в данном случае является очевидной, т.к.

и составляет 73,2 %, что, конечно же, является экономически неоправданным и с точки зрения проектировщика недопустимым. В связи с этим сделаем второе приближение, уменьшив характерный размер a.

5. Зададим a = 0,0035 м. Тогда значение гибкости второго приближения будет равно = 87,631. Вновь воспользуемся таблицей коэффициентов снижения допускаемого напряжения (справочные данные) и выберем исходные значения для проведения линейной интерполяции:

при = 80 = 0,67

при = 90 = 0,59.

С учетом этих данных для = 87,631 получим:

6. Определенное нами значение второго приближения подставим в выражение и выясним, удовлетворяется ли теперь неравенство. Имеем:

что подтверждает наличие устойчивого деформирования и отсутствие потери устойчивости и при уточненных размерах. Однако недонапряжение стойки в данном случае также является чрезмерным, поскольку

и составляет 28,8 %, что также является недопустимым. Поэтому необходимо сделать еще одно приближение, уменьшив (теперь уже незначительно) характерный размер a.

7. Зададим a = 0,0032 м. При этом значение гибкости третьего приближения будет равно = 95,847. Вновь воспользуемся таблицей коэффициентов снижения допускаемого напряжения (справочные данные) и выберем исходные значения для проведения линейной интерполяции:

при = 90 = 0,59

при = 100 = 0,50.

С учетом этих данных для = 95,847 получим:

8. Определенное нами значение третьего приближения подставим в выражение и выясним, удовлетворяется ли неравенство. Имеем:

что подтверждает наличие устойчивого деформирования и отсутствие потери устойчивости и в данном случае. Проверяя возможное недонапряжение стойки, имеем

что составляет 2,1% и является допустимым. Поэтому выбранный нами ранее размер a = 0,0032 будем считать окончательным. С учетом этого размеры сечения стойки определятся следующим образом:

B = 12,8 мм, H = 9,6 мм, b = 3,2 мм и h = 6,4 мм.

9. Определим теперь, каков же реальный коэффициент запаса устойчивости для подобранного нами поперечного сечения. Напомним, что критическое напряжение σ_кр при продольном сжатии стержней в общем случае не может быть определено по какой-либо одной наперед заданной формуле, поскольку его величина (как и сами формулы) является функцией гибкости стержня.

По таблице (справочные данные) для материала Сталь 5 . Так как гибкость стержня , то для вычисления следует использовать формулу Эйлера. Имеем:

Площадь подобранного ранее сечения составляет , а именно

.

Очевидно, что критическая нагрузка в рассматриваемом примере будет равна

.

Поделив на Р, получим искомую величину коэффициента запаса устойчивости

Пример 12.

Подобрать размеры круглого поперечного сечения стержня длиной из дерева (сосна), нагруженного силой Р = 100 кН, если Один конец стержня жёстко защемлён, а другой свободен от закрепления

Решение.

Условия устойчивости записываем в виде

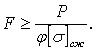
Подбор диаметра D сечения производим методом последовательных приближений.

Первое приближение.

Принимаем Тогда:

Так как то

Подбор диаметра ведём с точностью до целого см. Для найденного диаметра D = 13см находим:

Находим гибкость По таблице коэффициентов (справочные данные) с учётом интерполирования находим

Вычисляем:

Сравнивая с , видим, что в стержне будет перенапряжение в или на 429%. Поэтому следует рассмотреть второе приближение.

Второе приближение.

Задаёмся новым значением:

Находим

Диаметр Далее после округления размера диаметра до целых значений см вычисляем:

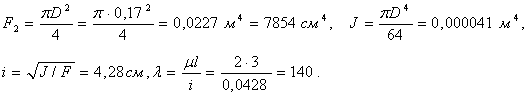
По таблице находим и рассчитываем:

Перенапряжение составляет т.е. 83%. Поэтому необходимо рассмотреть третье приближение.

Третье приближение.

Принимаем

Вычисляем:

Находим диаметр

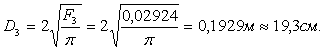
Округляем диаметр до целых значений см и получаем D3 = 20см. Корректируем новую площадь:

Вычисляем:

По таблице для находим с учётом интерполяции Расчётное сопротивление:

Недонапряжение т.е. 7,7%.

На этом расчёт можно прекратить и принять размер диаметра D = 20 см.

Пример 13.

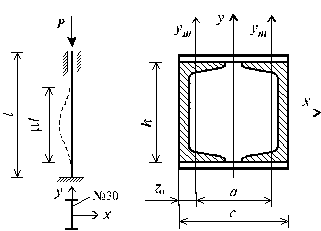
Заданную стойку двутаврового (№30) поперечного сечения центрально сжатую силой Р (рис. а), рассчитать на устойчивость, а также указать положительные и отрицательные стороны конструкции этой стойки. В целях минимизации расходов материальных ресурсов можно заменить двутавровое сечение стойки более рациональным сечением из двух швеллеров, соединенных планками на сварке (рис. б). Подобрать сечения из двух швеллеров и сравнить результаты по площади с сечением из двутавра. Материал стоек - сталь Ст.3, расчетное сопротивление при растяжении R = 1,9×10⁵ кПа.

Решение:

1. Расчет на устойчивость стойки из двутавра. Проверка устойчивости сжатых стержней производится по формуле . Из сортамента ГОСТ 8239-72 выписываем необходимые данные для двутавра №30: A = 46,5×10^-4 м²;  = 0,123 м; = 0,0269 м.

Тогда из формулы имеем:

. (1)

Для нахождения величины нужно знать максимальную гибкость стойки, которая определится из формулы

,

где l₀ - приведенная (свободная) длина стойки, . Здесь - коэффициент приведенной длины, зависящий от способа закрепления концов стойки (для нашего примера  = 0,5), l - длина стойки; i_min - минимальный радиус инерции сечения стойки (в данном случае - радиус инерции относительно оси y). Таким образом,

.

По таблице коэффициентов (справочные данные) находим при  = 55,76, интерполируя до третьего знака после запятой:

при  = 50: = 0,89;

при = 60: = 0,86.

Поэтому при = 55,76

Подставляя значения A, и R в формулу (1), получим допустимое значение сжимающей силы с точки зрения устойчивости рассматриваемой стойки:

.

Преимуществом стойки из двутавра является простота конструкции и малая трудоемкость изготовления и монтажа, недостатком - неравная устойчивость в разных плоскостях.

2. Подбор сечения стойки из двух швеллеров. При рассмотрении этого вопроса составное сечение стойки следует рассматривать как цельное, и поэтому расчет приведенной гибкости можно не выполнять. Подбор составного сечения стойки будем производить путем последовательного приближения. Для этого задаемся произвольным значением , подбираем сечение и сопоставляем возникающие в нем напряжения с расчетным сопротивлением. Эта операция производится до тех пор, пока напряжение, возникающее в стойке, будет достаточно близким к расчетному сопротивлению (отклонение не должно превышать).

Примем  = 0,6. Из (1) определим требуемую площадь F сечения двух швеллеров:

; .

По ГОСТ 8240-72 принимаем швеллер № 24а, для которого

м2, м, м.

Для обеспечения равноустойчивости стойки из двух швеллеров нужно, чтобы гибкость ее была примерно одинаковой в обеих плоскостях. Для принятого сечения из двух швеллеров определим максимальную гибкость:

.

По таблице коэффициентов (справочные данные) находим значение для полученной гибкости:

при = 10: = 0,99;

при = 20: = 0,97.

Для = 15,24:

;      A = 2 Aшв = 0,00658 м2.

Определяем напряжение в стойке:

Недонапряжение составляет

Необходимо уменьшить сечение стойки. Принимаем стойку из швеллеров № 20 (F_шв = 0,00234 м²; i_x = 0,0807 м). Определим гибкость:

По таблице коэффициентов (справочные данные) для =18,59 находим: = 0,973, и учитывая, что A = 2A_шв = 0,00468 м², получим:

кПа £ R.

Недонапряжение составляет

Принимаем стойку из швеллеров №18 (A = 0,00207 м²;  = 0,0724 м), гибкость которой принимает значение:

По таблице коэффициентов (справочные данные) для = 20,72 находим: = 0,973; A = 0,0414 м²:

кПа.

Перенапряжение составляет

, что допустимо.

Окончательно принимаем стойку из двух швеллеров №18. Из сортамента ГОСТ 8240-72 выписываем необходимые данные:

I_x = 1090×10^-8 м⁴, I_y = 86×10^-8 м⁴, z₀ = 0,0194 м, h = 0,18 м, b = 0,07 м.

Момент инерции поперечного сечения стойки из двух швеллеров относительно оси x: Момент инерции составного сечения относительно оси y можно изменять, сближая или удаляя швеллеры один относительно другого. Определим расстояние между швеллерами из условия, что . Из рис.  б имеем с = а +2×z₀ , где а - расстояние между собственными осями y каждого из швеллеров. Тогда:

,

отсюда

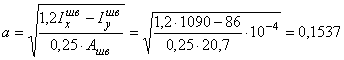м.

Монтажное расстояние между швеллерами будет с = а + 2×z₀  = = 0,1537 + 2×0,0194 = 0,1925 м, принимаем c = 0,192 м. Сравнивая сечение из двух швеллеров с заданным двутавровым, видим, что площадь заданного сечения составляет 46,5×10^-4 м², а полученного из двух швеллеров - 41,4×10^-4 м². Таким образом, расход металла на стойку из двух швеллеров (без учета металла на соединительные планки) будет меньше в 46,5/ 41,4 = 1,12 раза, или на 12, чем на стойку из одного двутавра.

Однако конструкция стойки из двух швеллеров трудоемка в изготовлении по сравнению со стойкой из двутавра. Экономическое преимущество подобранного сечения стойки, состоящего из двух швеллеров, по сравнению с двутавром, объясняется более рациональным распределением ее изгибных жесткостей в различных направлениях. Это приводит к выравниванию значений моментов инерции относительно главных центральных осей инерции сечения и тем самым, к равноустойчивости стойки в указанных направлениях.

Это положение является важным обстоятельством для разработки оптимальных конструктивных решений с позиции устойчивости.

Пример 14.

Для стального стержня с заданной формой поперечного сечения (см. рис.), сжатого силой N = 500 кН, требуется найти размеры поперечного сечения. Материал стержня – сталь C255. Длина стального стержня l = 4 м. Принять, что коэффициент условий работы .

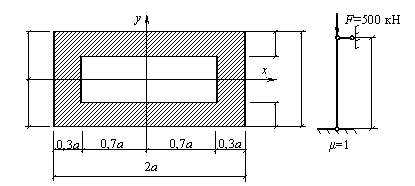
Решение.

Определяем

(1)

(2)

(3)

Принимая в качестве первого приближения , получаем из формулы

Используя формулу (1), находим 1,44а² = 0,00417, тогда геометрический параметр а = 0,0538 м. Из выражения (3) определяем

i_min = 0,3325a == 0,01789 м.

Формула дает

Материал стержня – сталь С255, следовательно, В этом случае из табл. 1

Таблица 1

Гибкость	Коэффициент для элементов
	из стали с Ry, МПа		из чугуна	из древесины
	240	280
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220	0,987 0,962 0,931 0,894 0,852 0,805 0,754 0,686 0,612 0,542 0,478 0,419 0,364 0,315 0,276 0,244 0,218 0,196 0,177 0,161 0,147 0,135	0,985 0,959 0,924 0,883 0,836 0,785 0,724 0,641 0,565 0,493 0,427 0,366 0,313 0,272 0,239 0,212 0,189 0,170 0,154 0,140 0,128 0,118	0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,565 0,16	0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12

находим для Разница между и значительная, поэтому повторяем расчет, принимая

а по формуле (3) находим: i_min=0,3325a == 0,0225 м. Затем из выражения определяем:

Из табл. 1 для стали с и берем Разница между и составляет

Повторяем расчет в третий раз, принимая

тогда Разница между и составляет 6,6%.

Обычно считается, что разница не должна превышать 5%, поэтому, повторяя расчет в четвертый раз, получаем ; А₄ = 0,00833 м²; а = 0,0761 м; i_min = 0,0253 м; В этом случае разница между и получилась равной 0%. Следовательно, принимаем за окончательный результат значение а = 0,0761 м. Напряжение в поперечном сечении стержня (см. рис.) равно при этом

Пример 15.

Подобрать элемент решетки фермы с l = 100 см. Продольная сила N = 50 кН. Элемент решетки принять в виде одиночного равнобокого уголка. Материал решетки – сталь С245,

Решение.

Согласно условию задачи определяем l_ef по формуле l_ef = 0,8l,: Для стали C245 имеем . Принимая в качестве первого приближения из условия находим

Из сортамента выбираем равнобокий уголок 45455 мм с = 4,29 см². Так как , то в качестве i_min принимаем i_x = 1,37 см, тогда гибкость стержня = 80/1,37 = 58. В этом случае из табл. 1 определяем Разница между и – значительная, поэтому повторяем расчет, принимая = (0,5 + 0,812)/2 = 0,656.

Следовательно, условие дает А₂ = 2,083/0,656 = 3,18 см². Выбираем равнобокий уголок 40404 мм с = 3,08 см² и i_min = i_x =1,22 см. В этом случае = 80/1,22 = 66, а .

Напряжение в поперечном сечении стержня получается при этом

.

По формуле находим

Недонапряжение составляет (186 – 62)100%/ 186 = 13%. Делаем еще одну попытку. Принимаем новое среднее значение коэффициента продольного изгиба = (0,7744 + 0,656) / 2 = 0,7152, тогда А₃ = 2,91 см². Выбираем уголок 36364 мм с = 2,75 см² и i_min = i_x = 1,09 см. Тогда 80/1,09 = 74, а В этом случае

Перенапряжение составляет (182 – 175)100% / 175 = 4% < 5%, что допустимо. Окончательно, для элемента решетки фермы оставляем равнобокий уголок 36364 мм.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00