Главная
Лекция 3 (продолжение). Задачи
для самостоятельного решения
Задача
1.
На какой площадке растянутого стержня касательное напряжение равно по величине нормальному?
Задача
2.
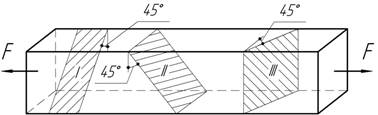
Какие напряжения возникают на заштрихованных площадках при растяжении стержня квадратного сечения bxb?
Задача
3.
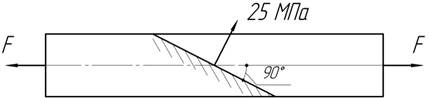
Чему равно наибольшее нормальное напряжение в стержне, если на данной площадке оно равно 25 МПа?
Задача
4.
Чему равно наибольшее касательное напряжение в стержне, если на данной площадке оно равно 80 МПа?
Задача
5.
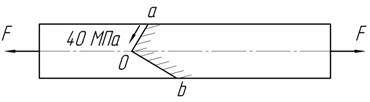
Определить величину и направление касательного напряжения на площадке аb?
Задача
6.
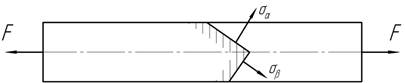
Какова величина силы F, растягивающей стержень прямоугольного
сечения 5х2 см, если 
Задача
7.
Достаточна ли прочность растягиваемого стержня, если нормальное напряжение в поперечном сечении равно 140 МПа, а наибольшее касательное напряжение не должно превышать 60 МПа?
Задача
8.
При растяжении силой F=50 кН наибольшее касательное напряжение в стержне равно 40 МПа. Какую силу может безопасно выдержать стержень, если [σ]=160 МПа?
Задача
9.
Какие напряжения (нормальные или касательные) определяют несущую способность растягиваемого стержня, если [σ]=160 МПа, [τ]=100 МПа?
Задача
10.
Чему равны нормальные и касательные напряжения на площадке ob?
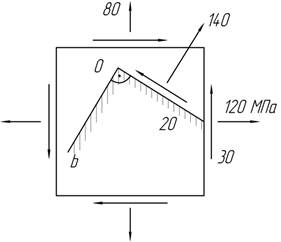
Задача
11.
Не прибегая к аналитическим выражениям для напряжений на произвольной наклонной площадке, определить указанные ниже величины (размерность напряжений - МПа).
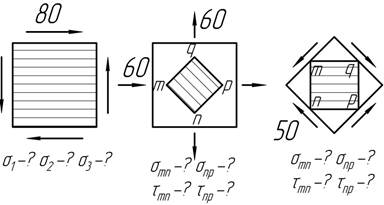
Задача
12.
Углы квадратной пластины толщиной t нагружены сосредоточенными силами F, направленными вдоль диагоналей. Определить напряжения на гранях элемента mnpq, выделенного в центре.
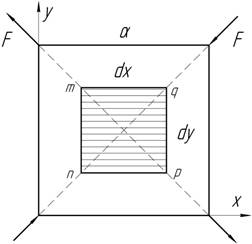
Задача
13.
Пользуясь круговой диаграммой Мора, определите величины и направления главных напряжений (размерность напряжений - МПа).
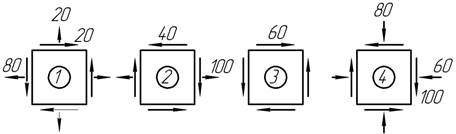
Задача
14.
В соответствии с заданной круговой диаграммой Мора воспроизведите напряжение на гранях элемента (размерность - МПа).
Задача
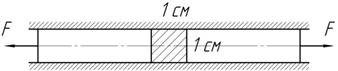
15.
Резиновый стержень сечением 1х1 см плотно вставлен между двумя стальными плоскостями и сжимается силами F=200 Н. Определить давление, производимое стержнем на плоскости, если ν=0,5.
Задача
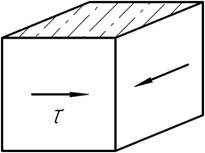
16.
Насколько изменится объем кубика со стороной а, нагруженного по 4 граням касательными напряжениями τ? Упругие постоянные материалы известны.
Задача
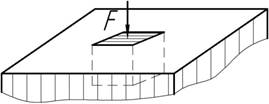
17.
Пробковый кубик свободно, но без зазора, вставлен в гнездо кубической формы 1х1х1 см, сделанное в сьальной плите, и сжимается силой F=10 Н, приложенной к свободной грани. Чему равны напряжения на гранях кубика, если для пробки ν=0?
Задача
18.
Кубик со стороной а вставлен в гнездо абсолютно жесткой плитой с зазорами Δа и 2Δа. При этом он выступает на 3Δа над поверхностью плиты. Под действием давления, приложенного к выступающей грани, зазоры перекрываются, причем в момент закрытия последнего зазора верхняя грань кубика оказывается на уровне поверхности плиты. Чему равен коэффициент Пуассона материала кубика, считая, что для него справедлив закон Гука?
Задача
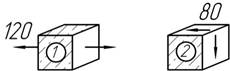
19.
Для какой точки
коэффициент запаса прочности больше, если 
Задача
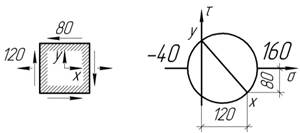
20.
Достаточна
ли прочность чугунной детали, в опасной точке которой возникает приведенное на
рисунке напряженное состояние? Дано: 
Задача
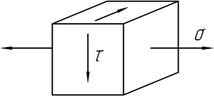
21.
Запишите
условие прочности для данной точки, полагая σ=0,5τ. Рассмотреть 2 случая: а)
материал пластичный, для которого 
б) материал хрупкий, для которого 
Задача
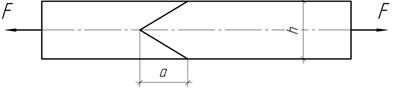
22.
Наиболее
благоприятные условия работы клеевого соединения имеют место, если нормальные
напряжения в плоскости шва в 1,5 раза выше касательных. Какую
для этого следует выбрать длину a соединения?
Задача
23.
Найти,
под каким углом α к оси стержня надо приклеить тензорезистор
1, чтобы его показания при растяжении стержня были вдвое меньше показаний тензорезистора 2, расположенного вдоль оси стержня.
Коэффициент Пуассона материала стержня ν=0,25.
Задача
24.
Докажите,
что при осевом сжатии стержня абсолютное изменение объема не
зависит от площади поперечного сечения.
Задача
25.
Как
изменится первоначально прямой угол, нанесенный на поверхности стержня, при его осевом растяжении силами F? Дано: F, G, A.
Задача
26.
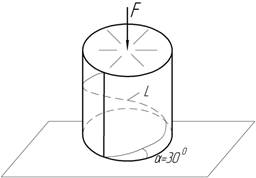
Цилиндрический образец диаметром d сжимается в процессе. Замерено изменение диаметра Δd. Вычислить абсолютное изменение длины L одного витка винтовой линии с углом подъема, равным α=30 0С, если коэффициент Пуассона материала равен ν. При каком угле α длина витка не меняется?
Задача
27.
При
каком соотношении между напряжениями 
в данной точке возникает линейное напряженное состояние?
Задача
28.
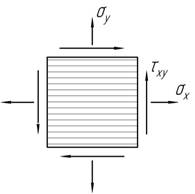
Чему равно отношение нормальных напряжений, действующих на произвольно ориентированных взаимно перпендикулярных площадках?
Задача
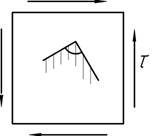
29.
Насколько изменится длина l упругого стержня, если на участке длиной а его нагрузить всесторонним давлением р? Упругие константы материала известны.
Задача
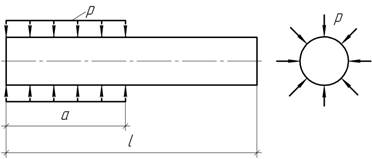
30.
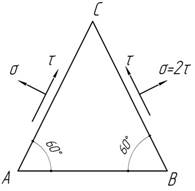
С
помощью каких напряжений, приложенных к грани АВ, можно
уравновесить пластину? Учитывая, что материал пластины хрупкий, проверить ее
прочность по 2-й гипотезе прочности. Дано: ν=0,25; σ=2τ=20 МПа; 
Задача
31.
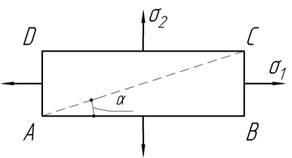
При
каком соотношении между напряжениями 
длины диагоналей элемента АВСД не изменяются, если
коэффициент Пуассона материала равен ν.
Задача
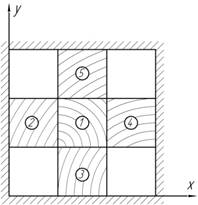
32.
Пять одинаковых кубиков помещены в абсолютно жесткую обойму. На средний кубик 1 действует давление р. Определить напряжения, возникающие на гранях кубиков. Упругие константы материала известны.
Задача
33.
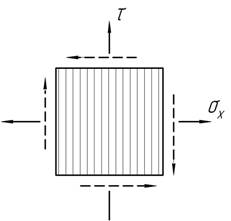
К
квадратному элементу приложены растягивающие напряжения 
,
равные допускаемым напряжениям для данного материала [σ]=100 МПа. Какое касательное напряжение τ нужно приложить по граням элемента,
чтобы коэффициент запаса уменьшился в 2 раза? Воспользоваться 3 гипотезой
прочности.
Задача
34.
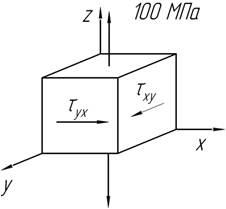
Какое
наибольшее значение касательных напряжений 
можно допустить, чтобы на любой наклонной
площадке куба касательное напряжение не превышало 80 МПа?
Задача
35.
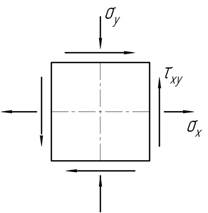
На гранях
плоского элемента действуют следующие напряжения: 
Вычислить допускаемые значения этих напряжений по
гипотезе прочности Мора при 
Во сколько раз изменяется величина допускаемой
нагрузки на элемент, если его выполнить из материала, для которого 
Задача
36.
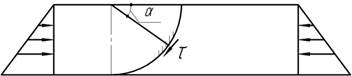
Полоса
склеена из двух однородных материалов по дуге окружности АВ. Во всех поперечных
сечениях напряжения распределяются по закону треугольника с наибольшей
ординатой 
Определить наибольшее касательное напряжение
на поверхности клеевого соединения и угол α, определяющий точку, в которой это
напряжение действует.
Задача
37.
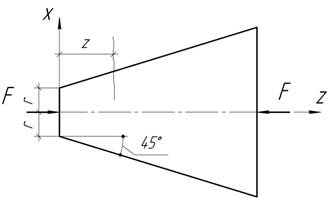
Стержень переменного сечения сжимается силами F. Покажите, что в поперечных сечениях и на площадках, параллельных оси стержня, возникают нормальные и касательные напряжения. Установите закон распределения напряжений и постройте их эпюры.
Задача
38.
При изучении свойств материалов при высоких давлениях было обнаружено, что при достаточно большом давлении прямой цилиндрический стержень, нагруженный давлением по цилиндрической поверхности и свободный с торцов, может разорваться с образованием шейки (рисунок б). Произойдет так называемое перекусывание. Объясните причины этого типа разрушения.
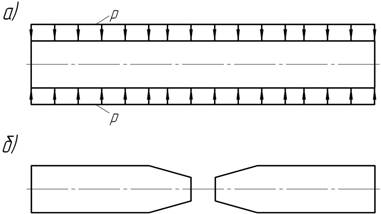
Задача
39.
Какой тип напряженного состояния (линейное, плоское или объемное) возникает в данной точке упругого тела? Определить величины и направления главных напряжений.
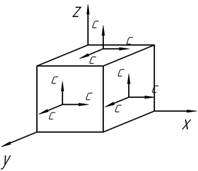
Задача
40.
Какое из двух напряженных состояний является более опасным с точки зрения 3-й и 4-й гипотез прочности? Материал является пластичным и одинаково работает на растяжение и сжатие.
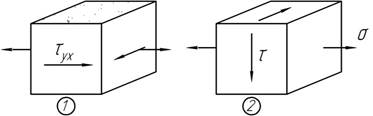
Задача
41.
Определить величину силы F, если нормальное напряжение в точке К сечения mn равно 75 МПа. Вычислить также наибольшее касательное напряжение в стержне.
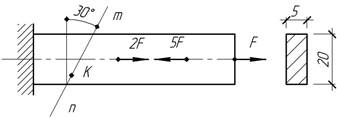
Ответ:
F=5 кН, 
Задача
42.
В
растянутом вдоль оси стержне нормальные напряжения по одному из наклонных
сечений равны 75 МПа, а касательные 43,3 МПа. Определить наибольшие нормальные напряжения
в стержне и угол наклона данной площадки по отношению к поперечному сечению.
Ответ:
Задача
43.
Стержень
прямоугольного сечения с отношением сторон 5:1 растянут вдоль оси силой F=320 кН. Определить размеры сечения, если допускаемое касательное
напряжение равно [τ]=80
МПа.
Ответ:
Сечение 2х10 см.
Задача
44.
Под
каким углом α к оси стержня надо наклеить тензорезистор
1, чтобы его показания при растяжении стержня были вдвое меньше показаний тензорезистора 2, расположенного вдоль оси стержня, если
ν=0,25?
Ответ:
Задача
45.
Наиболее
благоприятные условия работы клеевого соединения имеют место, если нормальные
напряжения в плоскости шва в 1,5 раза выше касательных. Какую
для этого следует выбрать длину соединения, если b=30 мм?
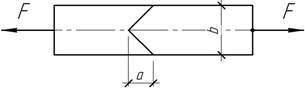
Ответ: а=10 мм.
Задача
46.
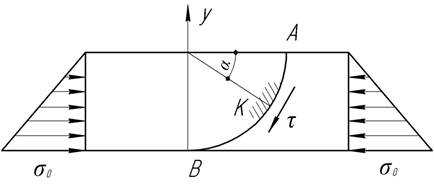
Полоса
склеена из двух однородных материалов по дуге окружности АВ. Во всех поперечных
сечениях напряжения распределяются по закону треугольника с наибольшей
ординатой 
.
Определите наибольшее касательное напряжение на поверхности клеевого соединения и угол
α, определяющий точку, в которой это напряжение действует.
Ответ:
Задача
47.
Стержень переменного сечения сжимается силами F. Покажите, что в поперечных сечениях и на площадках, параллельных оси стержня, возникают нормальные и касательные напряжения. Установите закон распределения и постройте эпюры напряжений.
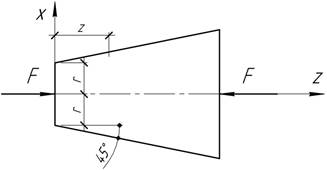
Ответ:
Задача
48.
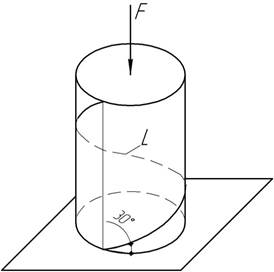
Цилиндрический
образец диаметром d=20
мм сжимается в прессе. Замерено изменение диаметра Δd=5
мкм. Вычислить абсолютное изменение длины L одного витка винтовой линии с углом подъема
α=300, если коэффициент Пуассона материала равен ν=0,25.
При каком угле 
длина витка не меняется?
Ответ:
ΔL=-4,5 мкм, 
Задача
49.
По граням оа и оb треугольного элемента действуют одинаковые нормальные напряжения, равные 50 МПа, а также касательные напряжения. Грань аb не нагружена. Определить значение касательных напряжений, а также величины и направления главных напряжений.
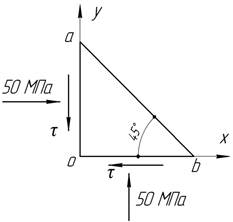
Ответ:
Задача
50.
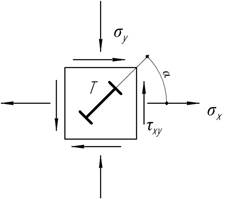
Элемент
нагружен по краям заданными напряжениями 
Определить, под каким углом 
надо установить тензометр Т,
чтобы он давал наибольшее показание при нагружении.
Найти наибольшее относительное удлинение 
при Е=70 ГПа и
ν=0,25 и соответствующее ему приращение показаний тензометра, имеющего базу s=100 мм и увеличение
К=500.
Ответ:
мм.
Задача
51.
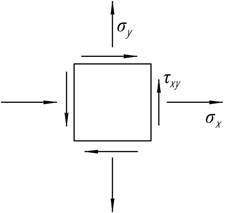
Плоский элемент
нагружен заданными напряжениями 
Найти направление, по которому отсутствует удлинение,
если Е=200 ГПа и ν=0,25.
Ответ:
Задача
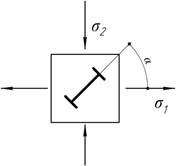
52.
Под
каким углом к направлению главного напряжения 
надо установить тензометр, чтобы он не изменял своего показания
при пропорциональном возрастании нагрузки?
Ответ:
Задача
53.
Элемент, вырезанный из стальной детали, находится в плоском напряженном состоянии. Определить изменение длины диагонали ab.
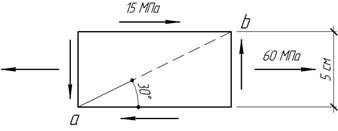
Ответ: Δd=28,7 мкм.
Задача
54.
При прохождении поезда через мост в одной из точек стальной
балки были измерены удлинения в горизонтальном и вертикальном направлениях: в
горизонтальном направлении разность отчетов оказалось равной +8 мм при базе
тензометра 20 мм и увеличения 1000; в вертикальном направлении разность отчетов
тензометра оказалось равной – 12 мм при его базе 100 мм и том же увеличении.
Определить нормальные напряжения в горизонтальном и вертикальном направлениях.
Ответ:
В горизонтальном направлении 
в вертикальном направлении 
Задача
55.
Квадратная
пластина 100х100 см в результате деформации получила приращение длин сторон 
Определить главные напряжения, удлинения вдоль диагоналей,
а также угол сдвига 
полагая Е=200 ГПа,
ν=0,3.
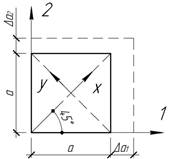
Ответ:
Задача
56.
Резиновый кубик свободно, но без зазора вложен в стальную форму, которую можно считать недеформируемой, и нагружен по верхней грани давлением Р=1 МПа. Определить напряжения на гранях кубика, относительные деформации его ребер, а также относительное изменение объема, если Е=7,5 МПа, ν=0,5.
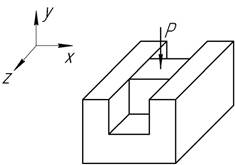
Ответ:
Задача
57.
По
заданным напряжениям 
и линейной деформации 
определить 
,
а также главные напряжения, если Е=100 ГПа, ν=0,3.
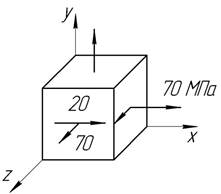
Ответ:
Задача
58.
По
заданным напряжениям и относительной линейной деформации 
определить 
,
а также главные линейные деформации, если Е=200 ГПа,
ν=0,3.
Ответ:
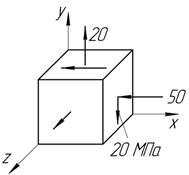
Задача
59.
На сколько удлинится упругий стержень, если Р=10 ГПа, а=100 мм, l=300 мм, Е=200 ГПа, ν=0,3.
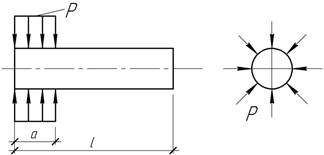
Ответ: Δl=3 мм.
Задача
60.
Алюминиевый
шар диаметром d=10
см помещен в камеру сверхвысокого давления. Определить, насколько изменится объем шара,
когда давление в камере достигнет величины Р=16 ГПа, если Е=70
ГПа, ν=0,36.
Ответ:
ΔV=100
см3.
Задача
61.
Медный
кубик со стороной 10 см без зазоров вложен в гнездо стальной плиты,
податливостью которой можно пренебречь. Под действием силы F
вертикальные ребра укорачиваются на 65 мкм. Определить величину силы F, если Е=100 ГПа, ν=0,34.
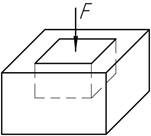
Ответ: F=1 МН.
Задача
62.
В толстой абсолютно жесткой плите просверлено сквозное круглое отверстие, через которую пропущена тонкостенная латунная трубка. Трубка вставлена в отверстие на столько плотно, что в пределах толщины плиты из-за трения продольные деформации трубки отсутствуют. Чему равны главные напряжения в отрезке трубки, проходящем через плиту, если трубка подвергается внутреннему давлению Р=17 МПа и ν=0,32.
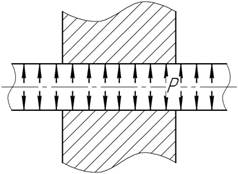
Ответ:
Задача
63.
На
короткий бетонный стержень диаметром d=10
см плотно надет стальной цилиндр с толщиной стенки 2 мм. Стержень сжат силами F=215 кН. Вычислить растягивающие напряжения, возникающие в
стальном цилиндре, если Еб=20 ГПа, 
Ответ:
Задача
64.
Бетонный
брус сечением 8х10 см заключен между двумя абсолютно жесткими плитами,
соединенными между собой четырьмя стальными стержнями сечением Ас=1
см2 каждый. Определить напряжение в стальных стержнях,
возникающие при нагружении бруса равномерно
распределенными по верхней и нижней граням давлением Р=15
МПа. Принять 
Ответ:
Задача
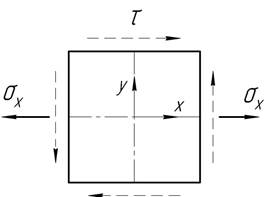
65.
К
квадратному элементу приложены растягивающие напряжения 
Используя
третью гипотезу прочности, определить касательные напряжения τ, которые
нужно дополнительно приложить по краям элемента, чтобы коэффициент запаса уменьшился в 2 раза.
Ответ: τ=86,6 МПа.
Задача
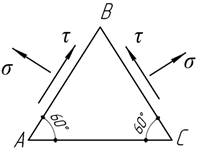
66.
На
гранях АВ и ВС тонкой пластины, изготовленной из хрупкого материала, действуют
равномерно распределенные напряжения σ и τ. Обеспечить равновесие пластины и
проверить ее прочность по 2-й гипотезе прочности, если ν=0,25,
σ=2τ=20 МПа, 
Ответ:
т.е. прочность недостаточна.
Задача
67.
Вычислить
допускаемые величины напряжений, действующих на гранях плоского элемента, если 
Во сколько раз изменится величина допускаемой нагрузки
на элемент, если его выполнить из материала, имеющие одинаковые напряжения на
растяжение и сжатие [σ]=150 МПа?
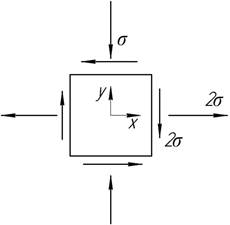
Ответ:
σ=25 МПа, 
Задача
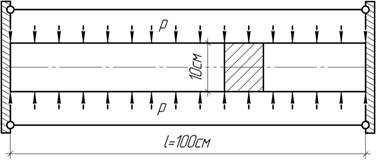
68.
Прямоугольный стальной брусок без зазора вставлен между двумя параллельными неподвижными стенками и нагружен по верхней и нижней граням давлением Р. Пользуясь 4-й гипотезой прочности, вычислить допустимую величину [Р], если [σ]=180 МПа, ν=0,25.
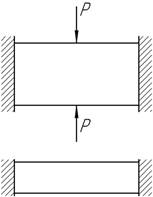
Ответ:
[Р]=200 МПа.
Задача
69.
В
какой точке напряженное состояние является более опасным? Воспользоваться гипотезой
Мора и рассмотреть два варианта: а) материал пластичный, для которого б) материал хрупкий, для которого 
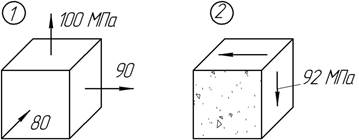
Ответ:
а) 
б) 
Задача
70.
Для
элемента, вырезанного из стальной детали, известны относительные деформации 
Определить величины и направления главных напряжений.
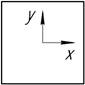
Ответ:
Задача
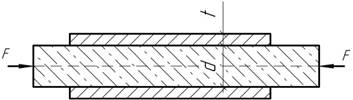
71.
Сжатый стержень состоит из двух частей, склеенных по плоскости АВ (см. рис.). При каком значении угла α (в пределах от 0 до 60°) он может выдержать наибольшую нагрузку, если для клея допускаемые напряжения [τ]=0,6[σ].
Принять, что прочность клеевого слоя определяется независимо по τα и σα.
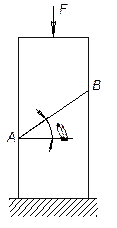
Ответ: Угол α=
31º.
Задача 72.
Бетонный кубик при сжатии разрушился по сечению, наклоненному на угол 45° к поперечному. Причем касательное напряжение в этом сечении оказалось 10 МПа. Определить сжимающее напряжение и разрушающее усилие, если размеры кубика 50х50х50 мм (см. рис.).
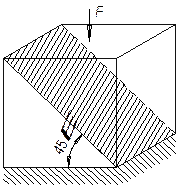
Ответ: Напряжение σmax=20 МПа, усилие F=50 кН.
Задача 73.
В оболочке тонкостенного цилиндра, нагруженного внутренним давлением, вырезан прямоугольный элемент (см. рис.). Напряжения по граням: σx= 50 МПа, σy= 100 МПа. Вычислить нормальное напряжение в сечении, где касательное напряжение τα= 14,3 МПа. Найти угол α, соответствующий этому сечению. Определить максимальное касательное напряжение.
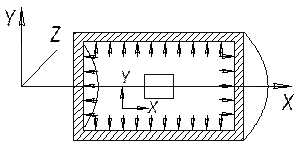
Ответ: Угол α= 17,50, нормальное напряжение σα= 54,6 МПа, максимальное касательное напряжение τmax = 25 МПа.
Задача 74.
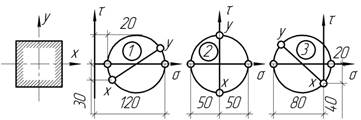
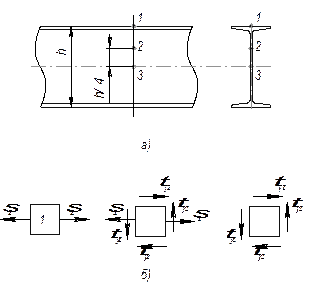
Напряженное состояние в точках 1,2,3 поперечного сечения двутавровой балки (см. рис. а) при изгибе в вертикальной плоскости
показано на рис. б. Определить характер напряженного
состояния, главные напряжения и положение главных площадок для указанных точек.
Напряжения в поперечном сечении: 
= 160 МПа, 
=
0; 
= 80 МПа, 
= 20
МПа; 
= 0, 
= 25 МПа.
Ответ: 1 – линейное: σ1 = 160 МПа, σ3 = 0; α1= 0°, α3 = 90о; 2 – плоское: σ1= 84,7 МПа, σ3= -4,7 МПа; α1 = 13°17/, α3 = 103°17/; 3 – плоское (чистый сдвиг): σ1=25 МПа, σ3= -2 МПа; α1 = 45°; α3 =135°.
Онлайн-калькулятор "Расчет по различным теориям прочности"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
