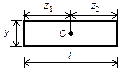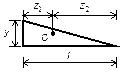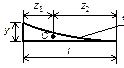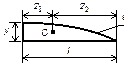Главная
Лекция
14. Построение эпюр в статически
неопределимых системах. Метод сил.
Содержание
Особенности статически неопределимых систем
и методы их расчета
Степень статической неопределимости системы
Канонические уравнения метода сил
Вычисление коэффициентов и свободных членов
канонических уравнений
Универсальная проверка коэффициентов и
свободных членов канонических уравнений
Построение окончательных эпюр внутренних
силовых факторов
Проверка окончательной эпюры изгибающих
моментов
Использование свойств симметрии при
раскрытии статической неопределимости
Определение перемещений в статически
неопределимых стержневых системах
Расчет статически неопределимых плоскопространственных систем методом сил
Особенности статически неопределимых систем и методы их расчета
Статически неопределимыми системами называются стержневые системы, для определения реакций опор в которых только уравнений равновесия недостаточно. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.
Для раскрытия статической неопределимости таких систем необходимо составлять дополнительные уравнения совместности деформаций. В предыдущих лекциях для расчёта отдельных статически неопределимых стержней, работающих на растяжение–сжатие, кручение, изгиб, использовалась группа соотношений, включающая в себя уравнения равновесия, геометрические и физические уравнения. Число таких уравнений определяется числом статической неопределимости стержневой системы. На рис.1 приведены примеры статически неопределимых балок и рам.
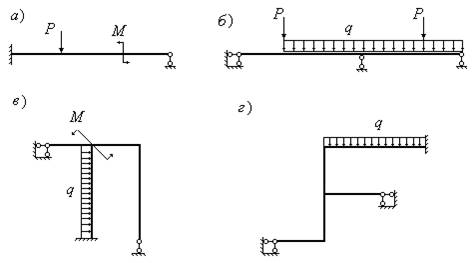
Рис.1
Балка, изображенная на рис.1,б, называется неразрезной балкой. Происходит это название оттого, что промежуточная опора лишь подпирает балку. В месте опоры балка не разрезана шарниром, шарнир не врезан в тело балки. Поэтому влияние напряжений и деформаций, которые балка испытывает на левом пролете, сказываются и на правом пролете. Если в месте промежуточной опоры врезать шарнир в тело балки, то в результате система станет статически определимой - из одной балки мы получим две независимые друг от друга балки, каждая из которых будет статически определимой. Следует отметить, что неразрезные балки являются менее материалоемкими по сравнению с разрезными, так как более рационально распределяют изгибающие моменты по своей длине. В связи с этим неразрезные балки получили широкое применение в строительстве и машиностроении. Однако, неразрезные балки, будучи статически неопределимыми, требуют специальной методики расчета, включающей в себя использование деформаций системы.
Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.
Статически неопределимые системы обладают рядом характерных особенностей:
1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.
Основными методами расчета статически неопределимых систем являются:
1. Метод сил. При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.
2. Метод перемещений. При расчете по методу перемещений основными искомыми величинами являются перемещения узловых точек, вызванные деформацией системы. Знание этих перемещений необходимо и достаточно для определения всех внутренних усилий, возникающих в поперечных сечениях элементов, заданной системы.
3. Метод конечных элементов. При расчете по методу конечных элементов система разбивается на простые конечные элементы и по матрице жесткости элемента и системы в целом устанавливается связь между перемещениями узлов элемента и системы и усилиями в них.
4. Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
5. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитических методов при расчете особо сложных систем используются различные численные методы.
В основе всех методов расчета упругих статически неопределимых систем, в том числе и рам, лежит желание уменьшить число совместно решаемых уравнений и числа неизвестных в них. Для этой цели из сложной системы выделяется более простая основная система, расчет которой является достаточно простым. Основная система отличается от заданной отсутствием некоторых связей или, наоборот, введенными в нее новыми абсолютно жесткими связями. Отброшенные связи заменяются в основной системе внешними, вначале неизвестными силами, приложенными по направлениям отброшенных связей, причем значения этих сил подбираются из условий отсутствия перемещений по направлениям отброшенных связей. Сформированная таким образом система уравнений называется системой канонических уравнений метода сил. Если же основную систему получают из заданной введением новых жестких связей, то неизвестными станут перемещения по направлениям этих связей, а условиями для составления уравнений – условия отсутствия реактивных сил во введенных связях. Составленные уравнения называют каноническими уравнениями метода перемещений.
В смешанном методе, основную систему получают из заданной исключением одних жестких связей и введением других. Неизвестными в канонических уравнениях смешанного метода являются усилия в отброшенных связях и перемещения по направлениям введенных связей, а условиями составления уравнений – отсутствие перемещений в основной системе по направлениям отброшенных связей и отсутствие реакций во вновь введенных связях. Таким образом, достигается эквивалентность заданной и основной систем в отношении перемещений узлов, а следовательно, и деформаций.
Недостатком введения основной системы является необходимость производить расчеты несколько раз: на действие заданной нагрузки и на действие каждого неизвестного перемещения по направлению введенных связей. Затруднения возникают и при вычислениях коэффициентов канонических уравнений и их свободных членов, они, впрочем, меньше при использовании ЭВМ.
Кроме указанной классификации, методы расчета статически неопределимых систем можно расчленить по степени их точности, по области работы материала сооружений, по особенностям расчетных операций и т.д.
По степени точности различают точные и приближенные методы расчета.
Точные методы базируются на обычных основных допущениях, принятых при расчете достаточно жестких сооружений (закон Гука, расчет по деформированной схеме, принцип сложения действия сил). Приближенные методы расчета, кроме обычных упрощений, используют дополнительные допущения, что обусловливает заметное отклонение от результатов точных методов расчета.
По области работы материала различают расчет сооружений в упругой стадии и расчет сооружений за пределом упругости. По особенностям расчетных операций методы расчета можно разделить на вычислительные и экспериментальные.
Теория расчета статически неопределимых систем играет особую роль в формировании профессиональных представлений инженера-строителя о работе реальных сооружений – ведь подавляющее большинство современных несущих строительных конструкций принципиально следует рассматривать именно как системы статически неопределимые. Строго говоря, в природе вообще не существует статически определимых систем, есть лишь некоторые статически определимые (после введения гипотез и предпосылок) задачи определения конкретных силовых факторов. Рекомендуется осознать это обстоятельство – с ним, в частности, могут быть связаны дополнительные возможности регулирования состояния конструкций.
Понимание того, что происходит с конструкциями в процессе их деформирования при
разнообразных воздействиях, позволяет обоснованно подходить к оценке их
состояния, надежности и экономичности,
целенаправленно вмешиваться в их работу, то есть осуществлять
регулирование и управление поведением конструкций – при этом в ряде случаев
удается полезно использовать такие эффекты и свойства, которые традиционно
считаются неблагоприятными. Ярким примером может
служить отношение к
факту чувствительности статически
неопределимых систем к кинематическим воздействиям (смещениям связей), в том числе к осадкам
опор. Известно, что, в отличие от систем статически
определимых, где смещения связей (равно
как и изменения температуры) не вызывают возникновения интегральных внутренних
силовых факторов – изгибающих и крутящих моментов, продольных и поперечных сил
и др. (перемещения и температурные
деформации при этом, конечно, возникают,
но они развиваются как свободные, нестесненные), в
системах с лишними связями усилия от упомянутых видов воздействий отличны от нуля. Если это воздействия
природного или техногенного происхождения, неподвластные нам в процессе эксплуатации сооружения,
то они, как правило, выступают в качестве неблагоприятных факторов, «отнимая» у
конструкций некоторую (иногда значительную) часть их несущей способности, что приводит
к увеличению расхода материала.
Но это же свойство статически неопределимых систем можно
заставить служить на пользу делу – если, задавая контролируемые смещения внешних или внутренних связей либо
искусственно создавая начальные
температурные поля в процессе сборки и монтажа конструкций, «подправлять»
усилия и напряжения, делая их распределение более равномерным и, следовательно,
более выгодным с точки зрения материалоемкости.
Другой отличительной особенностью статически неопределимых
систем, имеющей важное практическое
значение, является зависимость значений силовых факторов в разных сечениях
конструкции от соотношений и (при температурных и кинематических воздействиях)
числовых значений жесткостей элементов системы при разных видах их деформаций
(растяжении или сжатии, изгибе, сдвиге, кручении). Инженер, выполняющий расчет
конструкции или оценивающий состояние находящегося в эксплуатации сооружения, должен ясно представлять, какие
именно составляющие деформации существенно влияют на напряженно-деформированное
состояние системы, а какими можно пренебречь с допустимой погрешностью. Например, априори понятно, что на распределении усилий в
комбинированных системах (шпренгельных балках, рамах и арках с затяжками,
вантовых конструкциях и т.п.) ощутимо сказываются продольные деформации очень
гибких стержней, работающих на чистое растяжение без изгиба; в конст-рукциях с тонкостенными элементами и в ряде других
случаев значительным может быть влияние сдвига и т.д. Но лишь выполнив решение некоторых типовых
задач, можно убедиться раз и навсегда в том, что влияние этих факторов
настолько велико, что пренебрежение ими может радикально исказить
картину усилий и перемещений в системе.
Степень статической неопределимости системы
Перед расчетом статически неопределимой конструкции необходимо сначала определить степень статической неопределимости рассматриваемой системы. Для балок и простых рам степень статической неопределимости равна числу лишних опорных связей. В каждой связи возникает опорная реакция, поэтому степень статической неопределимости можно найти, сосчитав разность между количеством неизвестных опорных реакций и числом независимых уравнений статики.
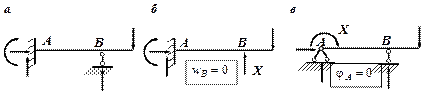
Рис.2
Например, балка на рис. 2, а является один раз статически неопределимой, так как имеет 4 связи и 4 неизвестные опорные реакции, а количество независимых уравнений равновесия – 3. В раме, показанной на рис. 4, а, число наложенных связей и опорных реакций в них равно 5, и эта рама является дважды статически неопределимой. Если в один из стержней балки (рамы) врезан шарнир, то количество связей уменьшается на единицу, так как становится возможным взаимный поворот сечений, примыкающих к шарниру. Появляется дополнительное уравнение для определения опорных реакций: "изгибающий момент в шарнире равен нулю" или можно сказать по-другому: "сумма моментов всех сил, расположенных слева (или справа) от шарнира, равна нулю". Так, балка с врезанным в точке Е шарниром, показанная на рис. 3, а, является один раз статически неопределимой: от 5 опорных связей надо вычесть одну связь, связанную с наличием дополнительного шарнира в точке Е. Из четырех оставшихся связей одна является лишней. Можно сосчитать степень статической неопределимости этой балки и иначе: для определения пяти опорных реакций можно составить четыре уравнения статики (дополнительное уравнение "изгибающий момент в шарнире Е равен нулю"). Разность между числом реакций и количеством уравнений статики равна единице, то есть балка один раз статически неопределима.
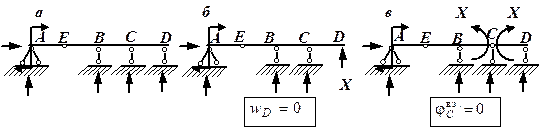
Рис.3
Рис.4
Лишние связи сооружений можно удалять, не нарушая их геометрической неизменяемости. Например, удалением опорных вертикальных связей В и С неразрезная балка преобразуется в консольный стержень, введением цилиндрических шарниров K и L – в статически определимую двухпролётную составную балку (рис. 4.1,а). Удалив из статически неопределимой фермы стержень 14 или 34, получим два варианта статически определимой шарнирно-стержневой системы с простой структурой (рис. 4.1,б). Статически неопределимая двухшарнирная рама после удаления горизонтальной связи опоры В превращается в ломаный стержень, прикреплённый к диску "земля" шарниром А и вертикальной связью, ось которой не проходит через шарнир А. Введением цилиндрического шарнира С эта же рама преобразуется в статически определимую трёхшарнирную раму (рис. 4.1,в).
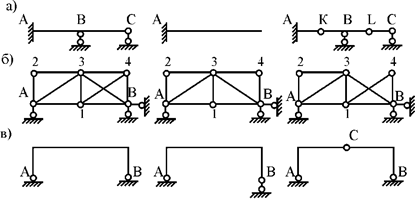
Рис.4.1
Особенностью всех лишних связей, удалённых из статически неопределимых систем, показанных слева на рис. 4.1, является то, что реакции в них от внешних воздействий с помощью уравнений статики определить нельзя. Эти связи называются условно необходимыми. Вместе с тем, в составе рассмотренных сооружений имеются связи, усилия в которых определяются из условий равновесия: горизонтальная связь опоры А неразрывной балки (рис. 4.1,а), стержни А2,23, А1, А3 фермы (рис. 4.1,б), вертикальные связи пятовых шарниров А и В рамы (рис. 4.1,в). Такие связи называются абсолютно необходимыми. Их удаление превращает заданное сооружение в геометрически изменяющую или мгновенно изменяемую систему.
Следует различать внешне статически неопределимые и внутренне
статически неопределимые системы.
Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т.е. лишние опорные закрепления. Примером внешне статически неопределимой плоской системы является трехпролетная рама (рис. 5).
Рис.5
Степень статической неопределимости внешне статически неопределимой системы S легко установить путем вычитания из общего числа опорных стержней m количество независимых уравнений равновесия n, которое может быть составлено для данной системы (одно - для одномерных; три - для плоских и шесть - для пространственных систем).
где C - число связей, накладываемых на конструкцию; У - число возможных независимых уравнений равновесия, которые можно составить для рассматриваемой системы.
Для плоской рамы, изображенной на рис.5, учитывая, что защемление эквивалентно трем опорным стержням, получаем:
C = 3 + 2
2 +1 = 8; n = C - У = 8-3 = 5,
т.е. данная система 5 раз статически неопределима.
Степень свободы при внешней статической неопределимости определяется по формуле:
W=2Ш+С0-3Д,
где Д – число жестких дисков, из которых состоит стержневая система;
Ш – число простых шарниров, соединяющих между собой жесткие диски. Если шарнир соединяет более двух дисков, то он называется кратным и равен d-1 простым шарнирам (d – число соединяемых дисков);
Со – число опорных стержней, наложенных на систему.
Правило (1) для определения степени статической неопределимости применяют только для простых систем. В более сложных случаях это правило не работает. На рис.6 представлена рама, степень статической неопределимости которой, пользуясь уравнением (1), определить невозможно.
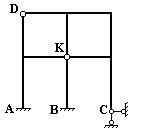
Рис.6
Внешне, система, приведенная на рис.6, пять раз статически неопределима. Это легко установить с помощью уравнения (1): из шести внешних связей (три в сечении А, три в сечении В и два в сечении С) вычитаются три возможные уравнения равновесия. Однако, эта система обладает еще и внутренней статической неопределимостью. Учесть внутреннюю статическую неопределимость с помощью уравнения (1) нельзя.
Внутренне статически неопределимой называют систему, обладающую лишними связями, введенными для взаимного соединения частей системы.
Прежде, чем перейти к определению степени статической неопределимости рамы, изображенной на рис.6, введем несколько определений. Первое из этих определений включает в себя понятие о простом шарнире.
Простым называется шарнир, соединяющий два стержня (рис. 7).
Рис.7. Простой шарнир
Шарнир, соединяющий несколько стержней, называется сложным (рис.8).
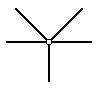
Рис.8. Сложный шарнир
Число простых шарниров, которые могут заменить один сложный шарнир, определим из формулы:
где CT - число стержней, входящих в узел.
Пересчитаем сложный шарнир, изображенный на рис.8 в число простых шарниров с помощью формулы (2): Ш=5-1=4. Таким образом, сложный шарнир, изображенный на рис.8, можно заменить четырьмя простыми шарнирами.
Введем еще одно понятие - замкнутый контур.
Докажем
теорему: любой замкнутый контур три раза статически неопределим.
Для доказательства теоремы рассмотрим замкнутый контур, нагруженный внешними силами (рис. 9).
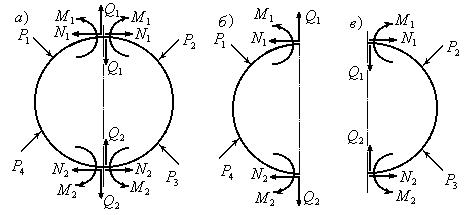
Рис.9
Разрежем замкнутый контур вертикальным сечением и покажем внутренние силовые факторы, возникающие в месте сечения. В каждом из сечений возникают три внутренних фактора: поперечная сила Q, изгибающий момент M и продольная сила N. Всего на каждую из отсеченных частей контура кроме внешних сил действуют шесть внутренних факторов (рис.9,б,в). Рассматривая равновесие одной из отсеченных частей, например, левой (рис.9,б), выясняем, что задача три раза статически неопределима, так как для отсеченной части можно составить всего три независимых уравнения равновесия, а неизвестных сил, действующих на отсеченную часть, шесть. Таким образом, степень статической неопределимости замкнутого контура равна n=6-3=3. Теорема доказана.
Теперь, используя понятие о простом шарнире и замкнутом контуре, можно сформулировать еще одно правило для определения степени статической неопределимости:
где K - число замкнутых контура; Ш - число шарниров в пересчете на простые (2).
Пользуясь уравнением
(3), определим степень статической неопределимости рамы, изображенной на рис.6.
Рама имеет пять контуров К=5, включая контур,
образуемый опорными стержнями. Шарнир в узле D простой, так как соединяет два
стержня. Шарнир в сечении К
– сложный, так как соединяет четыре стержня. Число простых шарниров, которые
могли бы заменить шарнир в сечении К, равно по формуле
(2): Ш=4-1=3. Шарнир С также
является сложным, так как соединяет три стержня. Для этого шарнира Ш=3-1=2. Кроме того, система имеет еще два простых шарнира,
с помощью которых крепится к основанию. Таким образом, число простых шарниров в
системе равно Ш=8. Подставляя число замкнутых контуров
К и число простых шарниров Ш в формулу (3) определяем
степень статической неопределимости рамы: 
.
Таким образом, изображенная на рис. 6 рама, семь раз статически неопределима. А
это означает, что для расчета подобной системы необходимо составить
дополнительно к трем уравнениям равновесия семь уравнений совместности
деформаций. Решая полученную таким образом систему из 10 уравнений относительно
неизвестных, входящих в эти уравнения, можно определить как величины реакций во
внешних связях, так и внутренние усилия, возникающие в раме. Процедуру решения
этой задачи можно несколько упростить, исключив из системы уравнений уравнения
равновесия.
Двухопорная рама с затяжкой (рис. 10, а) внутренне один раз статически неопределима. Статически определимая система (рис. 10, б) получена из заданной (рис. 10, а) путем разрезания затяжки ab. И при этом взаимодействие частей затяжки заменяется только одной неизвестной осевой силой N1. Следовательно, в статически определимой системе, изображенной на рис. 10, б имеем одно лишнее неизвестное N1 , которое невозможно определить при помощи метода сечений. Поэтому заданная система (рис. 10, а) является один раз статически неопределимой.
Если затяжку жестко заделать в стойки, как это показано на рис. 11, а, то получим трижды статически неопределимую систему.
Действительно, в данном случае после разрезания нижнего ригеля ab, взаимодействие частей ac и bc характеризуется уже тремя неизвестными усилиями N1, Q1, M1 (рис. 11, б), которые нельзя определить из условия равновесия. Поэтому система, изображенная на рис. 11, a является три раза внутренне статически неопределимой.
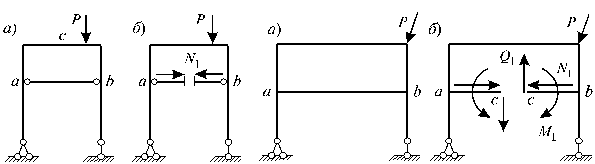
Рис.10
Рис.11
Отсюда можно сделать вывод, что в плоских системах, замкнутый бесшарнирный контур имеет три лишние связи. Следовательно, если плоская система содержит n замкнутых контуров, то она, очевидно, будет 3n раз статически неопределима.
На рис. 12 показана плоская рама, имеющая в первом (а) случае три внешние связи, а во втором случае (б) - пять. Значит, в первом случае рама имеет необходимое для статической определимости количество внешних связей, а во втором же - две дополнительные внешние связи. Однако в обеих ситуациях рама статически неопределима, т.к. конфигурация ее такова, что не позволяет определить усилия во всех ее элементах, используя только уравнения равновесия. Следовательно, для окончательного ответа на вопрос о статической определимости системы необходимо проведение совместного анализа наложенных на систему внешних и внутренних связей.
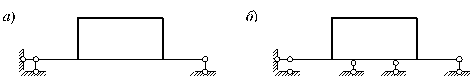
Рис. 12
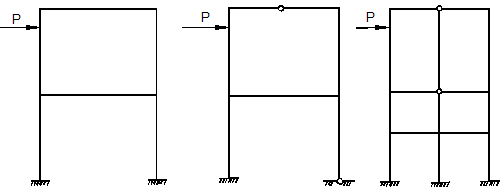
Рассмотрим другие рамы, которые содержат замкнутые контуры (рис. 13).
а)
б)
в)
Рис.13
Первая рама
(рис.13,а) имеет шесть простых
внешних связей при трёх необходимых для плоской системы. Следовательно, система
имеет Л = 6 – 3 = 3 лишние внешние
связи. Система имеет один замкнутый контур К= 1, который имеет три лишние
внутренние простые связи, т.е. трижды статически неопределим. Следовательно,
степень статической неопределимости системы 
.
Вторая рама (рис.13, б) имеет пять
внешних простых связей при трёх необходимых. Следовательно, Л=5–3=2 и система внешним образом дважды
статически неопределима. Система имеет два замкнутых контура К=2, каждый из которых трижды
статически неопределим, следовательно, внутренним образом система 
шесть раз была бы статически неопределима,
если бы не было внутреннего шарнира. Последний
соединяет три стержня (m = 3) и поэтому даёт системе (m – 1) = 3–1=2 степени свободы. Таким образом, степень
свободы статической неопределимости второй рамы можно вычислить по общей
формуле:
где Ш0 – число простых врезанных шарниров, К – число замкнутых контуров, Л – число лишних внешних связей.
В результате
получаем: 
Третья рама
(рис.13, в) имеет Л = 9 – 3 = 6, К = 4, Ш0 = 2 + 3 = 5, следовательно, 
Отметим, что степень статической неопределимости стержневой системы и её степень свободы связаны равенством n=-N.
Рассмотрим еще несколько примеров определения степени
статической неопределимости стержневых и рамных систем.
Балка, изображенная на рис.1,а, является один раз статически неопределимой, так как имеет три связи на левой опоре и одну связь на правой опоре. Независимых уравнений равновесия для такой балки можно составить только три. Таким образом, степень статической неопределимости балки n=4-3=1. Неразрезная балка, изображенная на рис.1,б также один раз статически неопределима, так как обладает двумя связями на левой опоре и по одной связи на промежуточной опоре и на правой опоре – всего четыре связи. Таким образом, степень ее статической неопределимости n=4-3=1.
Рама, изображенная на рис.1,в, три раза статически неопределима, так как обладает шестью связями в опорах. Независимых уравнений равновесия для этой рамы можно составить только три. Таким образом, степень статической неопределимости для этой рамы равна: n=6-3=3. Степень статической неопределимости рамы, изображенной на рис.1,г равна четырем, так как рама обладает семью связями на опорах. Следовательно, степень ее статической неопределимости равна n=7-3=4.
Степени статической неопределимости балки (рис. 14,а) и рамы (рис. 14,в) с учетом общего числа замкнутых контуров по формуле (3) будут:
− для балки: n=3К-Ш=32–5=1;
− для рам: n=3К-Ш =32–4=2, n=3К-Ш =32–4=2.
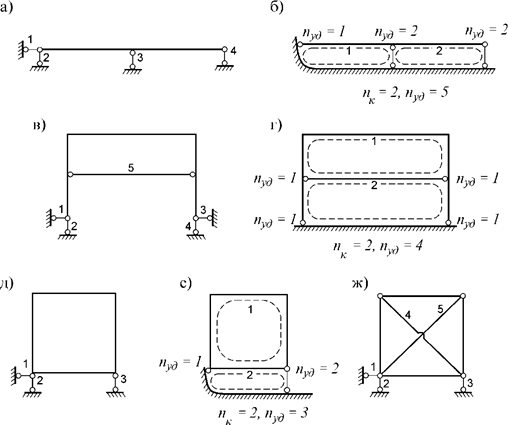
Рис.14
Число контуров и простых шарниров зависит от способа представления расчётной схемы сооружения. На рис. 15,а,б показано изображение расчётной схемы одной и той же рамы с различным количеством контуров и простых шарниров. Естественно, что степень статической неопределимости рамы не зависит от способа изображения её расчётной схемы. Действительно:
n= 3К-Ш = 33
– 3 = 6 (рис. 15,а),
n = 3К-Ш = 35
– 9 = 6 (рис. 15,б).
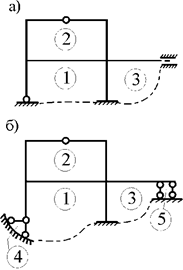
Рис.15
Рассмотрим еще пример. Используя формулу "контуров", вычислим степень статической неопределимости плоских стержневых систем, изображённых на рис. 16.
На рис. 16,а,б цифрами, объединёнными кружками, пронумерованы замкнутые контуры. Рядом с цилиндрическими шарнирами цифрами помечено количество простых шарниров.
n= 3К-Ш = 33
– 8 = 1 (рис. 16,а),
n= 3К-Ш = 39
– 24 = 3 (рис. 16,б).
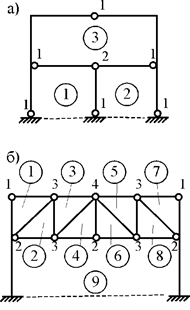
Рис.16
На рис. 17 показано несколько рам. Последовательно
рассмотрим их.
а) Рама имеет четыре дополнительные внешние связи и три
взаимные связи, т. е. семь раз статически неопределима (рис.17,а).
б) Полагаем сначала, что шарнир А
отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи.
Система без шарнира А была бы пять раз
статически неопределимой (рис.17,б).
Шарнир А принадлежит
одновременно трем стержням. Его можно рассматривать как два совпавших шарнира.
Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения
относительно другого, то можно сказать, что шарнир А
снимает две связи. Система становится, таким образом, вместо пяти — три раза
статически неопределимой.
Обобщая сказанное, можно сделать вывод, что шарнир снимает
число связей, на единицу меньшее числа сходящихся в нем стержней. В данном
случае в шарнире А сходятся три стержня и
шарнир снимает две связи.
Рис.17. Примеры рамных
статически неопределимых конструкций:
а) статически неопределимая —
семь, б) — три, в) — четыре, г) — три,
е) — двенадцать, ж) — семь, и) — тридцать раз статически неопределима
в) Если бы шарнир А
отсутствовал, система была бы четыре раза внешним образом и три раза внутренним
образом статически неопределимой, т.е. всего семь раз. Шарнир
А снимает число связей, на единицу меньшее числа сходящихся в нем
стержней, т. е. три связи. Рама четыре раза статически неопределима (рис.17,в).
г) Рама три раза статически неопределима (рис.17,г).
д) Внешние связи не удовлетворяют условиям кинематической
неизменяемости. Это — механизм, точнее говоря, мгновенный механизм. Система
имеет возможность поворачиваться относительно верхней опоры как жесткое целое
Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет
достигнуто какое-то положение равновесия, но новое положение связей будет
зависеть от жесткости системы. К раме неприменимы основные принципы
сопротивления материалов: принцип неизменности начальных размеров и принцип
независимости действия сил (рис.17,д).
е) Рама — пространственная. Имеется шесть дополнительных
внешних связей (лишняя заделка) и шесть дополнительных взаимных связей
(замкнутый контур). Система 12 раз статически неопределима (рис.17,е).
ж) Система семь раз статически неопределима (один раз
внешним образом и шесть раз — внутренним) (рис.17,ж).
з) Здесь для плоской рамы не показаны внешние связи, но
дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае
условились считать, что дополнительных внешних связей нет, и положение рамы в
пространстве считается определенным; рассматриваются только внутренние связи.
Система три раза статически неопределима (рис.17,з).
и) Здесь также рассматриваются только внутренние связи,
поскольку система указанных внешних сил удовлетворяет условиям равновесия.
Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной
стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного
замкнутого контура. Таких сечений следует сделать пять (см. рис. 17, и).
Система 30 раз статически неопределима.
Метод сил
Наиболее широко применяемым в машиностроении общим методом
раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том,
что заданная статически неопределимая система освобождается от дополнительных
связей как внешних, так и взаимных, а их действие заменяется силами и
моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в
системе соответствовали тем ограничениям, которые накладываются на систему
отброшенными связями. Таким образом, при указанном способе решения неизвестными
оказываются силы. Отсюда и название «метод сил».
Алгоритм расчета методом сил
Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:
1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему канонических уравнений, т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.
Выбор основной системы
Система,
освобожденная от дополнительных связей, становится статически определимой. Она
носит название основной системы. После того
как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные
силовые факторы, которые принято называть лишними неизвестными. В тех сечениях, где
запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые
смещения, вводятся моменты. Как в том, так и в другом случае неизвестные
силовые факторы будем обозначать Xi, где i — номер
неизвестного. Наибольшее значение i равно степени статической
неопределимости системы. Заметим, что для внутренних связей силы Xi,
— являются взаимными. Если в каком-либо сечении рама
разрезана, то равные и противоположные друг другу силы и моменты прикладываются
как к правой, так и к левой частям системы.
Выбор основной системы (ОС) является непростым. Неудачный выбор основной системы может привести к значительной трудоемкости решения, а иногда и к грубой ошибке. Нельзя руководствоваться только одним правилом образования основной системы, а именно, что число отбрасываемых связей должно быть равным степени статической неопределимости. Надо обязательно следить еще и за тем, какие связи отбрасываются. Некоторые связи отбрасывать недопустимо. При выборе основной системы надо следить кроме всего прочего и за геометрической и кинематической неизменяемостью всей системы и отдельных ее частей.
Так, у балки (рис. 16,а), которую далее будем называть заданной системой (ЗС), степень статической неопределимости n=1. Если исключить лишнюю связь (правую опору) и обозначить неизвестную реакцию через X, получим ее основную систему (ОС) (рис. 18,б).
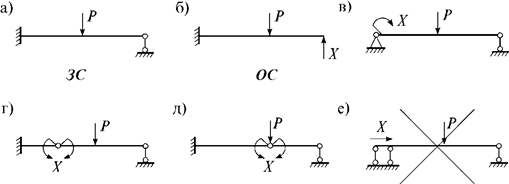
Рис.18
Способов исключения лишних связей очень много (теоретически – бесконечное число). Например, лишнюю связь можно исключать как на рис. 18,в-е. Однако одна из этих схем (рис. 18,е) геометрически изменяема и для дальнейшего расчета непригодна. Все остальные схемы могут быть приняты за основную систему.
Если воспользоваться известным теоретическим положением о том, что в линейно-упругих системах внешняя нагрузка распределяется единственным образом, то результаты расчетов по различным основным системам должны быть одинаковыми. Однако объем вычислений в разных основных системах может быть разным. Поэтому из многих вариантов основной системы нужно выбирать наиболее оптимальную. Например, в нашем примере первый вариант основной системы (рис. 18,б) предпочтительнее остальных, т.к. в ней эпюры строятся легче.
Для рамы, показанной на рис. 19, можно предложить основные
системы, а), б),..., которые получены
путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с
тем нужно помнить, что не всякая система с семью отброшенными связями может
быть принята как основная. На рис. 20 показано три примера для той же рамы, в
которой также отброшено семь связей, однако сделано это неправильно, так как
оставшиеся связи не обеспечивают кинематической неизменяемости системы (рис.20,
а, б), с одной стороны, и статической
определимости во всех узлах,— с другой (рис.20, в).
Рис.19
Рис.20
Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.
1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.21, б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.21, а).
2. Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n = 3 (рис.22, а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.22, б).
3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.22, в). В частных случаях (рис.22, г) рассечение стержня по шарниру освобождает две связи (рис.22, д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.22, е).
Рис.21
Рис. 22
Рассмотрим еще примеры образования основных систем метода сил для статически неопределимых рам (рис. 23-30). Вычислим сначала степень статической неопределимости этих рам, используя формулу (3) n= 3К-Ш:
рис. 23,а – n= 3К-Ш = 33
– 6 = 3;
рис. 24,а – n= 3К-Ш = 33
– 7 = 2;
рис. 25,а – n= 3К-Ш = 23
– 5 = 1;
рис. 26,а – n= 3К-Ш = 43
– 8 = 4;
рис. 27,а – n= 3К-Ш = 33
– 7 = 2;
рис. 28,а – n= 3К-Ш = 33
– 4 = 5;
рис. 29,а – n= 3К-Ш = 33
– 6 = 3;
рис. 30,а – n= 3К-Ш = 23
– 3 = 3.
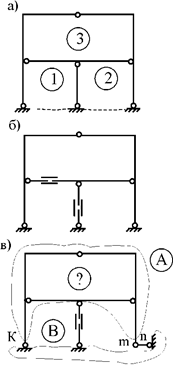
Рис.23
Рис.24
Рис.25
Рис.26
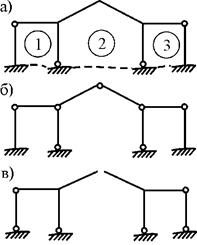
Рис.27
Рис.28
Рис.29
Рис.30
Основные системы метода сил из заданных статически неопределимых рам получены различными способами: удалением опорных связей (рис. 23,в; рис. 24,в; рис. 25,б; рис. 26,б), введением простых или кратных цилиндрических шарниров (рис. 23,б; рис. 25,в; рис. 26,в; рис. 27,б; рис. 29,б), введением поступательных шарниров, как правило, в элементы, имеющие по своим концам цилиндрические шарниры (рис. 23,б; рис. 24,б,в; рис. 29,б,в), удалением всех или части внутренних связей в цилиндрических шарнирах (рис. 30,б), разрезом по "живому" сечению (рис. 28,в) и другими способами, включая различные сочетания вышеперечисленных.
Для заданной расчётной схемы статически неопределимого сооружения существует множество вариантов основных систем метода сил. Для расчёта принимается вариант, удовлетворяющий ряду требований, среди которых обязательным является требование геометрической неизменяемости основной системы метода сил. С этой точки зрения основные системы метода сил, показанные на рис. 23,в и рис. 24,в не могут быть использованы для расчёта заданных статически неопределимых рам. Основная система метода сил, изображённая на рис. 23,в, по своей структуре геометрически изменяема, так как состоит из двух дисков А и В, соединённых между собой тремя параллельными связями ab, cd, ef одинаковой длины. На рис. 24,в показан вариант мгновенно изменяемой основной системы метода сил. Действительно, в этом варианте диск А и диск "земля" В соединяются между собой цилиндрическим шарниром К и связью mn, ось которой проходит через шарнир К.
Выполнение некоторых желательных требований при выборе основной системы метода сил способствует сокращению времени на расчёт статически неопределимого сооружения. Это, прежде всего, образование простых по структуре основных систем методом сил, где чётко просматриваются рабочие схемы (главные и второстепенные части), легко определяются реакции опорных связей и внутренние усилия. С этой точки зрения основная система метода сил, показанная на рис. 25,б, предпочтительнее, чем другая основная система (рис. 25,в) для этой же рамы.
Важно, чтобы в используемой для расчёта основной системе метода сил эпюры внутренних усилий не "растекались" по всем элементам, т.е. были бы локализованы, и имели бы возможно меньшие по абсолютной величине ординаты. Часто выполнению этого условия способствует введение цилиндрических шарниров в узлы статически неопределимых систем (рис. 26,в и рис. 28,б).
Для симметричных статически неопределимых сооружений основную систему метода сил следует выбирать также симметричной (рис. 28,б,в и рис. 29,б).
Для основных систем неконсольного вида необходимо в первую очередь вычислить, пользуясь уравнениями равновесия, опорные реакции, а затем, приняв их за внешние силы, построить эпюры. Для избежания ошибок всегда следует проводить проверку правильности вычисления опорных реакций.
Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого раздела. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.
Основную систему с приложенными к ней лишними неизвестными Х1, Х2 ,...Xn и внешней нагрузкой Р называют эквивалентной системой при условии, что её действительные перемещения согласуются с наложенными на исходную систему связями. Для каждой статически неопределимой заданной системы (рис. 31, а) можно подобрать, как правило, различные основные системы (рис. 31, б, в), однако их должно объединять следующее условие - основная система должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою геометрию без деформаций элементов).
Рис.31
Канонические уравнения метода сил
В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.
Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:
где первый
индекс означает направление перемещения и номер отброшенной связи, а второй
указывает на причину, вызвавшую перемещение, т.е. 
- это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; 
- перемещение по направлению i-ой связи, вызванное одновременным
действием всей внешней нагрузки.
В методе сил
реакцию k-ой связи принято обозначать
через 
.
С учетом этого обозначения и в силу справедливости
закона Гука перемещения можно
представить в виде:
где 
-
единичное (или удельное) перемещение по направлению i-ой связи, вызванное
реакцией 
т.е.
реакцией, совпадающей по направлению с Xk, но равной единице.
Подставляя (6) в (5), получим:
Физический смысл уравнения (7): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.
Записывая выражения, аналогичные (7), для всей совокупности n отброшенных связей, получим систему канонических уравнений метода сил. Уравнения имеют стационарную (каноническую) форму, одинаковую для всех статически неопределимых систем.
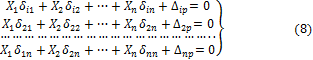
Здесь 
– единичные коэффициенты (перемещения); 
– моменты от единичных сил, приложенных в
направлении неизвестных 
;
EI –
изгибная жесткость. Обобщенные перемещения 
называются грузовыми коэффициентами
(перемещениями); 
– изгибающий момент, вызываемый i-й единичной силой; 
– изгибающий момент, который вызван системой
внешних сил.
Единичные
коэффициенты делятся на главные, расположенные по главной диагонали и имеющие
одинаковые индексы (
),
и побочные (
).
Главные коэффициенты всегда положительные, в отличие от побочных.
Симметрично расположенные коэффициенты в соответствии с теоремой о взаимности
перемещений равны друг другу, т.е. 
,
это свойство называется законом парности
коэффициентов при неизвестных.
Вид уравнения (8), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.
Вычисление коэффициентов и свободных членов канонических уравнений
Этому этапу
расчета предшествует построение единичных и грузовых эпюр внутренних силовых
факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся
от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей
лишней неизвестной в эквивалентной системе, и обозначаются через 
,
а единичная эпюра – через .
Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.
Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.
При вычислении
коэффициентов и свободных членов канонических уравнений метода сил, кроме
непосредственного интегрирования и применяют различные упрощенные приемы вычисления
интегралов. Особенно обстоятельно они разработаны для рам с прямолинейными
стержнями постоянного сечения. Жесткость EI = const при этом выносится за знак интеграла, а под
интегралом остается произведение двух функций: Mi и Mk , одна из которых, как правило, или обе являются линейными
функциями. Операция интегрирования здесь часто называется перемножением эпюр и
ее символически изображают следующим образом:
здесь знак 
означает умножение в смысле формулы Мора.
Применение готовых формул показано в таблице 1. Сами эти формулы без труда определяются элементарными методами. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпюрам, а также криволинейной с прямолинейной. Если любая из фигур, приведенных в табл. 1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что Мa = Мb .
При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в таблице 1.
Таблица 1
|
M2(x) M1(x) |
|
|
|
|
|
|
|
|
|
abl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, пусть нужно перемножить эпюры, приведенные на рис. 32. Каждую из эпюр можно представить в виде суммы: в первом случае, в виде двух треугольных и параболической; во втором -в виде двух треугольных.
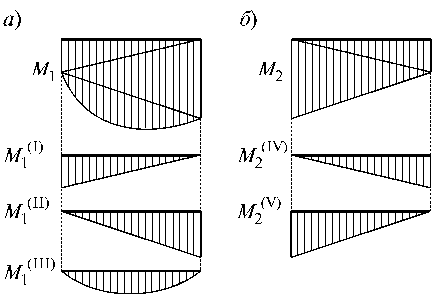
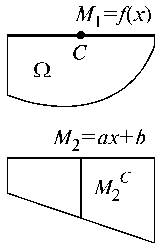
Рис. 32
Рис. 33
Тогда
А далее следует воспользоваться
формулой для вычисления интегралов 
, приведенных в таблице 1.
Довольно удобным способом перемножения эпюр
является способ Верещагина. Этот
способ применим в случае когда из двух перемножаемых
эпюр одна как минимум является прямолинейной. Если одна из эпюр является криволинейной вычисляется площадь 
криволинейной эпюры, которая умножается
на ординату под ее центром тяжести, взятую в прямолинейной эпюре 
(рис.33).
Предположим M1 = f (x); M2 = a x + b, тогда
но
величина 
представляет собой площадь криволинейной
эпюры, а величина
- статический
момент площади этой эпюры относительно левого конца стержня. Следовательно,
Известно, что величина 
представляет собой ординату центра тяжести
криволинейной эпюры, а
- значение
M2 при
.
В случае двух криволинейных эпюр способ Верещагина неприменим. Надо пользоваться интегралом Мора. Способ Верещагина применим также в тех случаях, когда одна из эпюр не криволинейная, а ломаная.
В таблице 2 приведены формулы для
определения площади , положения центра тяжести zC и ординаты yC в
центре тяжести для некоторых довольно распространенных плоских фигур.
В случае, когда имеются эпюры общего вида (например, обе эпюры криволинейные, либо трапеции, рис.33, разбиение уже на два равных интервала дает согласно формуле Симпсона точное выражение интеграла:
где индексы А и С относятся к сечениям расположенным на концевых сечениях интервала длиной l, а индекс В к серединному сечению того же интервала.
В тех случаях, когда функции M1 и M2 в рассматриваемом интервале длиной l, являются линейными и известны их значения в концевых сечениях интервала, то формулу перемножения M1 и M2 можно преобразовать в следующем виде:
Итак, после составления и решения канонической системы уравнений метода сил (7.4) мы получаем значения X1, X2, X3,..., Xn , т.е. значения усилий в лишних связях. Затем строим для основной системы эпюры изгибающих моментов от каждого из найденных усилий. Для этого могут быть использованы построенные ранее единичные эпюры, все ординаты которых необходимо теперь умножить на найденные значения соответствующих неизвестных.
Сложив по характерным сечениям (на протяжении всей рассчитываемой конструкции) ординаты эпюр от действия всех сил Xi с ординатами грузовой эпюры, получим окончательную (суммарную) эпюру изгибающих моментов в заданной статически неопределимой системе.
Таблица 2
|
№ |
Фигура |
Площадь |
Абсциссы центра тяжести |
|
|
z1 |
z2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Универсальная проверка коэффициентов и свободных членов канонических уравнений
Для выполнения
универсальной проверки необходимо построить суммарную единичную эпюру 
-
эпюру моментов от одновременного действия всех единичных сил, приложенных к
основной системе:
Перемножим
суммарную единичную эпюру с эпюрой :
Таким образом, результат перемножения суммарной и i-ой единичной эпюр - это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:
Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:
Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.
Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:
Таким образом, проверка свободных членов системы канонических уравнений (14.5) состоит в выполнении условия:
Построение окончательных эпюр внутренних силовых факторов
Окончательные эпюры можно построить двумя способами.
Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:
или, учитывая, что
приходим к выражению:
Аналогично определяется продольные и поперечные силы:
Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.
Недостатком
первого способа является то обстоятельство, что для его реализации необходимо
дополнительно построить эпюры 
,
которые не используются в расчете методом сил и поэтому не были построены
ранее.
В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (14) можно использовать в качестве дополнительной проверки.
Проверка окончательной эпюры изгибающих моментов
Эта проверка выполняется в двух вариантах: статическая и кинематическая.
При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Алгебраическая сумма моментов в любом узле должна быть равна нулю Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.
Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и внутренних усилий – должна быть равна нулю.
Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.
При умножении окончательной эпюры моментов на любую из единичных эпюр, возможных для данной рамы, должен получиться нуль, если в заданной раме в направлении соответствующего неизвестного перемещение невозможно.
При построчной
проверке каждая единичная эпюра моментов 
перемножается
с окончательной эпюрой моментов М:
Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:
Вариантом построчной проверки является проверка по замкнутому контуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.
Суммируя выражения типа (17) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:
т.е. результат перемножения суммарной единичной и окончательной эпюр моментов должен быть равен нулю.
Формулу (18) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.
Пример
1.
Требуется раскрыть статическую неопределимость балки и построить эпюры изгибающих моментов и поперечных сил (рис.34,а).
Решение.
В сечении А балка имеет
жесткую опору, исключающую перемещение и поворот сечения. Такая опора
соответствует наличию трех связей. На правом конце балка опирается свободно и
имеет одну связь. Таким образом, балка имеет четыре связи при трех степенях
свободы. Степень статической неопределимости балки равна единице.
Изобразим
балку и расставим “характерные” сечения: на левом конце, посредине и на правом
конце (рис.34,а). Оборвем одну связь
в сечении В и действие связи заменим реакцией 
(рис.34,б).
Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное
перемещение сечения В было равно нулю. В этом условии
будет заключаться эквивалентность исходной системы (рис.34,а) и статически определимой системе, изображенной на рис.34,б. Чтобы описать условие эквивалентности
двух систем, воспользуемся принципом независимости сил, сначала изобразим балку,
нагрузив ее только внешней нагрузкой (рис.34,в). Перемещение сечения В, вызванное
внешней нагрузкой, обозначим 
.
Далее изобразим балку, нагруженную
только сосредоточенной силой .
Перемещение сечения В, вызванное этой нагрузкой, обозначим 
.
Сумма этих перемещений должна равняться нулю, так как в исходной системе
сечение В в вертикальном направлении не перемещается:
Уравнение (19) удобно записывать в канонической форме:
где 
.
Здесь 
- перемещение, вызванное силой, равной единице,
приложенной в сечении В (рис.34,е).
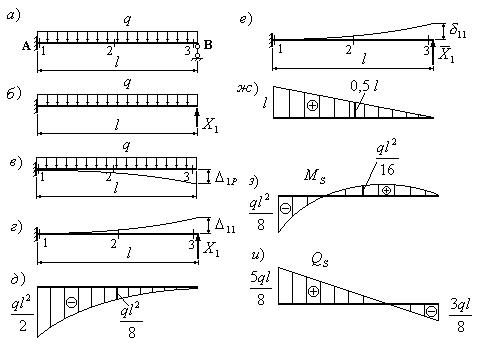
Рис.34
Неизвестную
реакцию можно определить из уравнения (20), если
предварительно найти перемещение ,
которое назовем грузовым, и перемещение ,
которое назовем единичным.
Чтобы
определить грузовое перемещение ,
построим грузовую эпюру изгибающих моментов (рис.34,д), единичную эпюру (рис.34,ж)
и перемножим их, воспользовавшись
формулой Мора-Симпсона:
В рассматриваемом примере:
Единичное
перемещение найдем, умножив единичную эпюру (рис.34,ж) саму на себя.
Для рассматриваемого примера
Подставляя
найденные значения для и в уравнение (20) и решая его относительно ,
найдем:
Суммарные изгибающие моменты в “характерных” сечениях балки найдем из выражения:
где n - число “лишних” неизвестных или степень статической неопределимости системы; i - номер “характерного” сечения.
Для рассматриваемой балки:
Откладываем найденные значения от базисной линии и строим эпюру суммарных изгибающих моментов (рис.34,з).
Для построения эпюры поперечных сил вырежем часть балки, расположенную между сечениями №1 и №3, приложим все действующие на вырезанный участок силы (рис.35) и составим два уравнения равновесия, из которых найдем значения поперечной силы в “характерных” сечениях, расположенных на границах вырезанного участка:
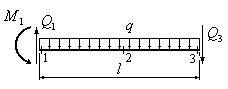
Рис.35
Учитывая, что
(знак момента учтен выбором его направления),
из первого уравнения находим: 
.
Из второго уравнения находим 
.
По найденным значениям строим суммарную эпюру поперечной силы (рис.34,и).
Пример
2.
Для балки (рис. 36,а)
определим внутренние усилия.
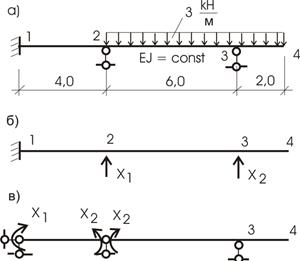
Рис.36
Решение.
1) Рассчитаем степень статической неопределимости n=5-3=2.
Два раза статически неопределимая балка. Основные
системы метода сил представлены на рисунке 36,б,в.
Для расчета примем вариант 36,в.
2) Запишем систему канонических уравнений:
3) Вычисляем коэффициенты 
и 
.
Эпюры от единичных загружений
представлены на рисунке 37,б,в и от внешней
нагрузки - на рисунке 37,г.
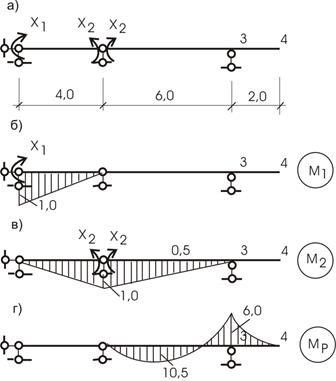
Рис.37
Решение системы:
дает 
По полученным значениям строим 
и 
(рис. 38,а,б)
и 
(рис. 38,в).
Проверки.
а) Статическая проверка. Значения моментов на опорах
(рис. 38,в) одинаковы и равновесие
обеспечивается. Проверка
удовлетворяется.
б) Кинематическая проверка.
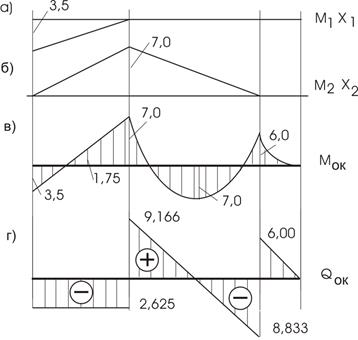
Рис.38
Перемножим 
с 
. Проверим, будет ли взаимный угол поворота сечений
балки на опоре 2 равен нулю?
Проверка удовлетворяется.
Эпюра 
строится по
эпюре по
рассмотренному ранее принципу. Выполните построение самостоятельно и свой
результат сверьте с приведенным решением на рис.38,г.
Пример
3.
Определить усилия (в кН) в стержнях фермы, изображенной на рис.39.
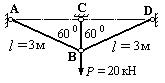
Рис.39
Решение.
1. Определяем степень статической неопределимости: n=3-2=1.
2. Выбираем основную систему (рис.40).Основная система получается из заданной путем рассечения одного из
стержней, например, стержня ВС.
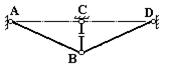
Рис.40. Основная система
3. Изображаем эквивалентную систему (рис.41).
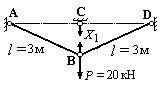
Рис.41. Эквивалентная система
Каноническое уравнение метода сил имеет вид:
Физический смысл этого уравнения состоит в том, что взаимное перемещение сечений, которые получились при рассечении стержня ВС, равно нулю.
4. Изображаем грузовое состояние системы (рис.42) и определяем усилия в стержнях фермы АВ и ВD.
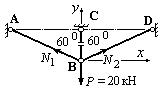
Рис.42. Грузовое состояние системы
Составляем уравнения равновесия сил на оси x и y:
откуда находим:
5. Изображаем единичное состояние системы (рис.43) и находим единичные усилия в стержнях фермы:
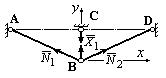
Рис.43. Единичное состояние системы
Составляем уравнения равновесия на оси x и y:
откуда находим:
6. Определяем грузовое и
единичное перемещения .
Для этого воспользуемся формулой Максвелла:
Из канонического уравнения (23)
находим “лишнюю” неизвестную :
Усилия в стержнях 
и 
найдем из формулы:
Подставляя в формулу (24) значения “лишней” неизвестной, грузовых и единичных изгибающих моментов, получаем:
Пример
4.
Определить реакцию опоры В рамы, изображенной на рис.44.
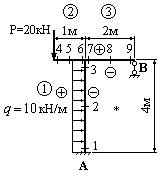
Рис.44
Следует отметить, что в заданной постановке можно избежать построения суммарных эпюр изгибающих моментов и поперечных сил для определения реакции опоры В. Для этого нужно выбрать таким образом основную систему, чтобы связь в опоре В оказалась “лишней”. Тогда “лишняя” неизвестная, заменяющая действие “лишней” связи, и будет искомой реакцией.
Решение.
1. Разбиваем раму на участки, выбираем точку наблюдения, вводим положительные и отрицательные стороны и проставляем “характерные” сечения.
2. Определяем степень статической неопределимости: n=4-3=1.
3. Выбираем основную систему.
Так как нас интересует реакция опоры В, принимаем в
качестве “лишней” неизвестной реакцию в этой опоре (рис.45).
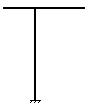
Рис.45. Основная система
4. Изображаем эквивалентную систему (рис.46).
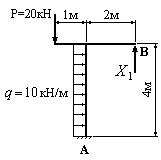
Рис.46. Эквивалентная
система
Каноническое уравнение метода сил имеет вид:
Физический смысл
этого уравнения – равенство нулю перемещений в направлении “лишней” неизвестной
,
вызванное самой “лишней” неизвестной и внешней нагрузкой.
5. Изображаем
грузовое состояние системы (рис.47,а)
и строим грузовую эпюру изгибающих моментов 
(рис.47,б).
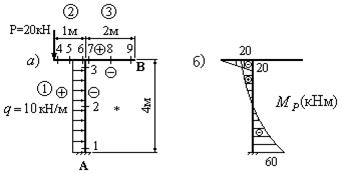
Рис.47
6. Изображаем
единичное состояние системы (рис.48,а)
и строим единичную эпюру изгибающих моментов 
(рис.48,б).
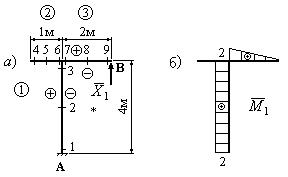
Рис.48
7. Перемножая грузовую эпюру 
и единичную эпюру 
изгибающих моментов по формуле Мора-Симпсона,
находим грузовое перемещение :
8. Перемножая единичную изгибающих моментов саму на себя, находим
единичное перемещение :
Подставляя (26) и (27) в уравнение (25) и решая его
относительно ,
получим:
Полученная значение для “лишней” неизвестной и есть величина опорной реакции В.
Положительный знак у реакции означает, что направление “лишней” неизвестной ,
а, следовательно, и реакции опоры В выбрано верно.
Пример
5.
Для заданной рамы (рис.49) требуется построить эпюры M, Q, N.
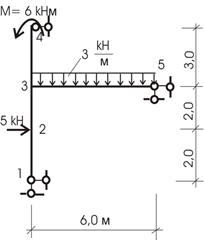
Рис.49
Решение.
1. Определяем степень статической неопределимости n=5-3=2
Для получения основной системы нужно отбросить 2 избыточные связи.
2. Выбираем основную систему.
Варианты основной системы приведены на рисунке 50, а,б,в,г.
Для расчета возьмем вариант 2 (выбор произвольный).
3. Запишем канонические уравнения для решения:
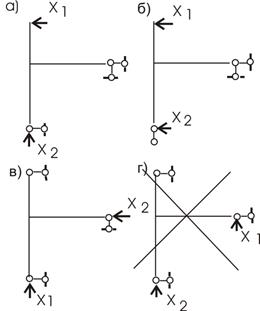
Рис.50
Для подсчета коэффициентов и свободных членов уравнений построим эпюры от единичных сил и внешней нагрузки (рис. 51,а,б,в,г).
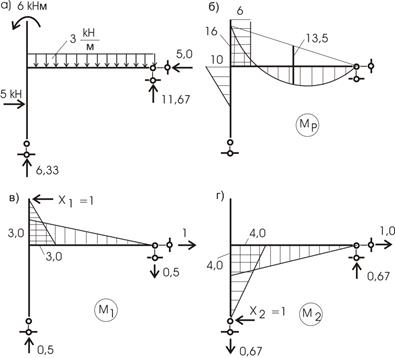
Рис.51
Вычисление основных параметров для построения эп. М от внешней нагрузки:
То же для построения М1.
И для построения М2.
4. Вычисляем коэффициенты при xi по правилу Верещагина:
Вычисляем грузовые слагаемые:
Перед решением системы уравнений производим проверку правильности вычислений коэффициентов:
а) построчная проверка
где 
- суммарная эпюра моментов от единичных сил
(рис. 52) и для первой строки
Равенство удовлетворяется.
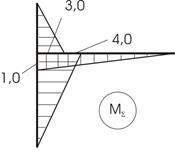
Рис.52
б) суммарная проверка.
Сумма всех коэффициентов = 
т.е.
т.е.
32,33=32,33.
Условие удовлетворяется.
в) проверка грузовых слагаемых
-8=-8.
Условие удовлетворяется.
5. Решение системы производим по методу Гаусса
Для этого разделим первое уравнение на 27, а второе – на 24. Получим:
Складываем оба уравнения:
Отсюда находим:
Подставляем х2 в любое уравнение системы:
Вывод: Неизвестная реакция х1 = - 1,21 направлена нами неправильно. Истинное направление реакции Н4 будет вправо, а направление реакции Н1 нами выбрано верно.
Дальнейший расчет может производиться двумя путями:
1) Приложив найденные усилия xi к основной системе совместно с внешней нагрузкой (рис. 53), строим обычным способом эпюры Мок, Qок, Nок . Опорные реакции H5, R5, R1 определяются из уравнений статики, и дальнейших пояснений не требуется.
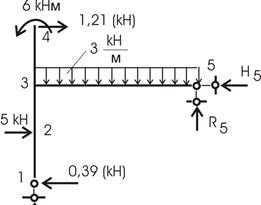
Рис.53
Построение этим путем мы предоставляем читателю для самостоятельного решения.
2) Используем принцип независимости действия сил, а именно:
Поскольку эпюры перерезывающих и продольных сил обычно не строятся ни от единичных сил, ни от внешней нагрузки, то эпюра перерезывающих сил Qок строится по эпюре изгибающих моментов Мок, а эпюра Nок - по эпюре Qок.
Рассмотрим этот путь расчета. Для этого построим эпюры Mixi (рис. 54,а,б) и рядом - Мр. (рис. 54,в). Результат построения - эпюра Мок (рис. 54,г).
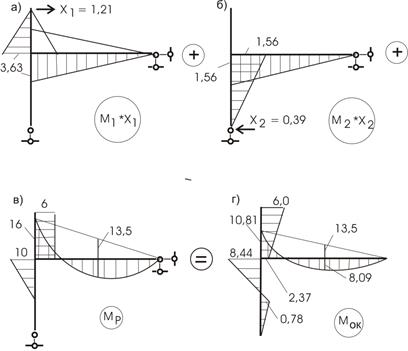
Рис.54
Проверим правильность построения эпюры Мок .
1. Статическая проверка.
Вырезаем узел 3 (рис. 55).
Составим уравнение статики
: 2,37+8,44-10,81=0
Условие удовлетворяется.
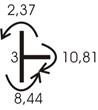
Рис.55
2. Кинематическая проверка.
Проверяем перемещение точки приложения силы xi по ее направлению. Оно должно быть равно нулю, что отвечает условию совместности деформации
Перемножим Мок на М1
Ошибка составляет
Условие удовлетворяется.
По эпюре Мок строим эпюру Qок. Для этого рассмотрим каждый стержень рамы, как отдельную балку, нагруженную системой сил: изгибающими моментами и внешней нагрузкой (рис.56).
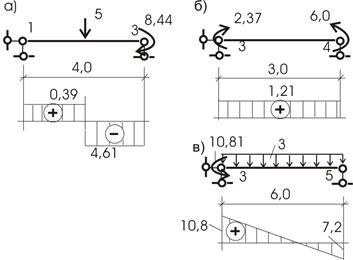
Рис.56
Построив обычным путем эпюры Q для каждого участка, сформируем эпюру Qок (рис.57,а). Эпюра Nок строится по эпюре Qок из условия равновесия узлов:
Вырезаем узел 4 (рис.58,а)
Вырезаем узел 3 (рис.58,б)
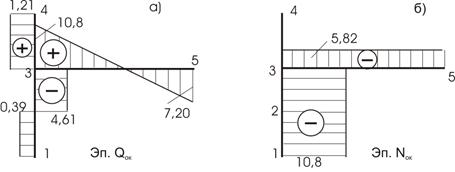
Рис.57
Рис.58
Эпюра Nок показана на рисунке 57,б.
Пример
6.
Требуется рассчитать конструкцию (рис. 59).
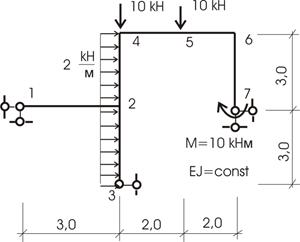
Рис. 59
Решение.
1. Определяем степень статической неопределимости n=5-3=2
Это говорит о наличии 2-х избыточных связей. Основная система для расчета получается удалением 2-х связей. Необходимо помнить о безусловно необходимых связях (их нельзя удалять) и условно необходимых, которые можно удалить.
Варианты основной системы приведены на рисунке 60. Варианты в) и д) использовать в дальнейших расчетах, как уже написано, нельзя, т. к. удалены безусловно необходимые связи и получаемая основная система мгновенно изменяемая!
Привычна по виду схема б), но оптимальной для дальнейшего расчета будет схема г). Примем ее за основную систему.
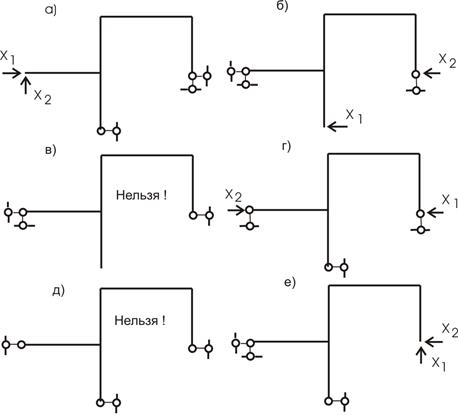
Рис.60
2. Для основной системы запишем канонические уравнения:
Каждое из этих уравнений гласит: суммарное перемещение
точки приложения неизвестных усилий по их направлению от воздействия всех сил,
действующих на конструкцию, равно нулю.
Здесь - перемещение точки приложения i-ой неизвестной по ее направлению от воздействия к-ой силы 
- перемещение точки приложения i-ой силы по ее направлению
от воздействия на конструкцию внешней нагрузки.
3. Для определения этих коэффициентов и грузовых
слагаемых строим эпюры изгибающих моментов от сил 
и от внешней
нагрузки (рис. 61).
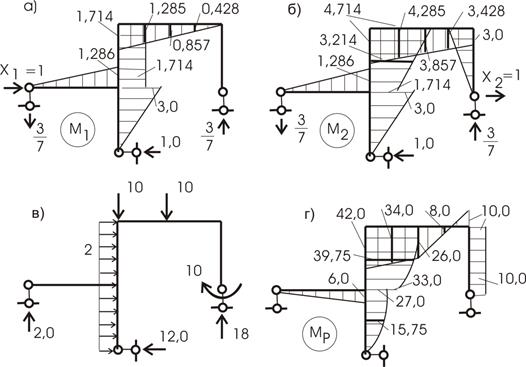
Рис. 61
Вычисляем 
:
Эпюру М1 перемножаем саму на себя:
Вычисляем 
. (Перемножаются эпюры М1 и М2 ):
Вычисляем 
.
(Перемножается эпюра М2 сама на
себя):
Вычисляем 
(перемножаются эпюры М1 на МР ):
Вычисляем 
.
(Перемножаются эпюры М2 на МР ):
4. Решение системы:
х1= -12,155 кH;
х2= -2,368 кH.
5. Построение эпюр внутренних усилий для заданной рамы.
1-ый путь построения.
К основной системе (рис. 62) приложим заданную
нагрузку и найденные усилия в отброшенных связях с учетом их знака. Для
полученной схемы строим эпюры внутренних усилий обычным путем (методами сопротивления
материалов).
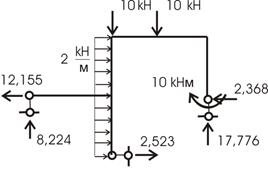
Рис.62
Определяем реакции в связях:
Тогда из второго уравнения 
Эпюры внутренних усилий М, Q и N показаны на рисунке 63,а,б,в. Читателю предлагается самостоятельно построить их и результаты сравнить.
6. Производим статическую проверку – равновесие узла должно сохраняться (рис. 63,г,д).
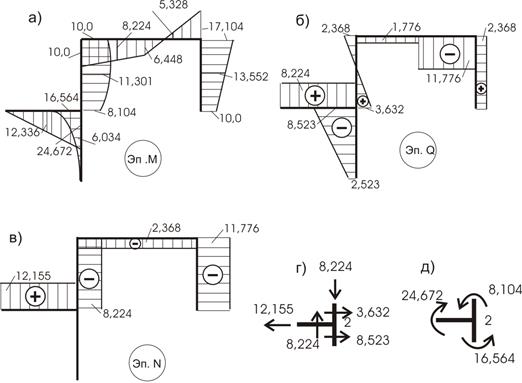
Рис.63
7. Кинематическая проверка.
где 
- одна из единичных
эпюр .
Перемножим (рис.63,а) на (рис. 61,а):
Процент погрешности составит:
2-ой путь
построения
Он основан на принципе независимости действия сил
(рис. 64).
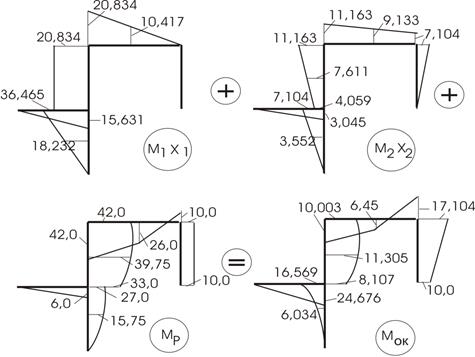
Рис.64
Сравнивая полученные результаты, по мы видим
небольшие погрешности вычисления. Следуя дальше вторым путем, эпюру Qоk строим
по эпюре Мок. Для этого
нашу раму расчленим на отдельные элементы (балки): 1 – 2; 2 – 3; 2 – 4; 4 – 6;
6 – 7, т. е. на 5 отдельных балок (рис.65). Загружаем их внешней нагрузкой и
моментами в жестких узлах, взятых из эпюры Мок (рис.64).
Разберем одну из балок, скажем, балку 2 – 4 (рис. 65,в). Для удобства расположим ее
горизонтально (рис. 65,е).
Определяем опорные реакции
По этим данным строим эпюру Q (рис. 65,е).
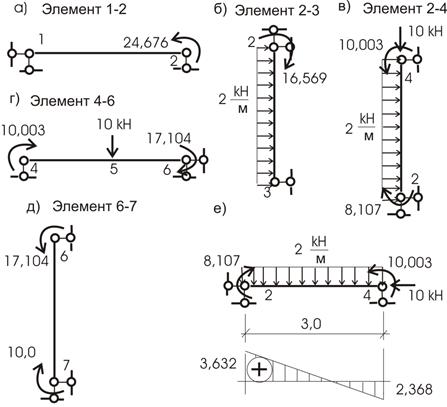
Рис.65
Сравнивая значения и
знаки (!) с эпюрой Qok, построенной ранее (рис. 63), на этом участке мы
видим полное совпадение.
Эпюру Nok строим
по эпюре Qok, используя способ вырезания узлов, как это делалось в
статической проверке, где мы показали это на примере одного узла. Используя
результаты Qок, построенной ранее, покажем на примере узла 4
определение продольных усилий в стержнях 4 – 2 и 4 – 6 (рис. 66).
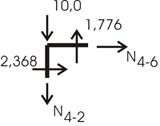
Рис.66
Cверим значения 
и 
со значениями,
найденными ранее (рис. 56,в)
– они полностью совпадают.
Пример
7.
Приведем пример расчета рамы без пояснений (рис. 67).
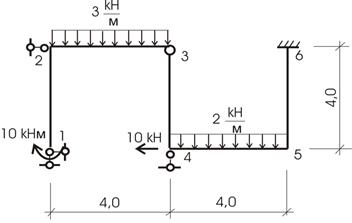
Рис.67
Решение.
1) Определяем степень статической неопределимости
2) На рис. 68 приведены варианты основных систем.
Делаем выбор на варианте а).
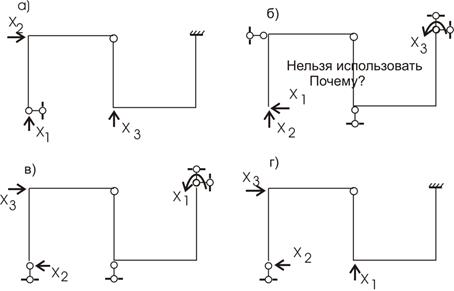
Рис.68
3) Канонические уравнения метода сил
Строим единичные эпюры.
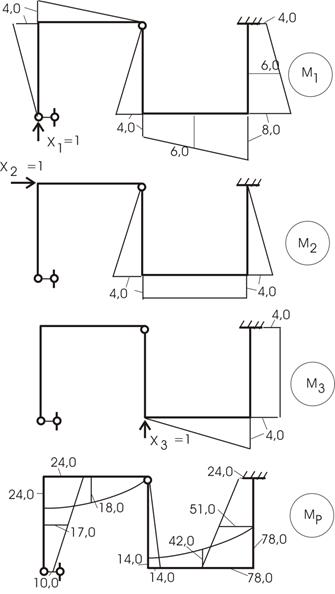
Рис.69
Определяем коэффициенты канонических уравнений:
Система уравнений:
Решаем систему уравнений.
Получаем: 
Загружаем конструкцию найденными усилиями и внешней
нагрузкой (рис. 70). Окончательные эпюры внутренних усилий приведены на рис.
71.
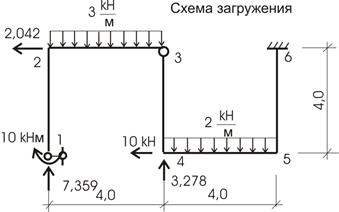
Рис.70
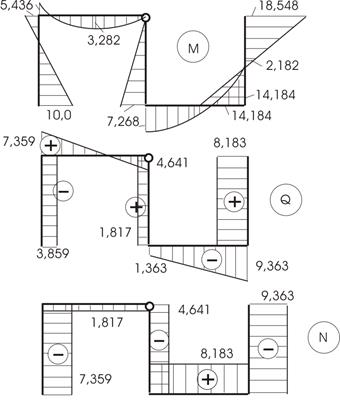
Рис.71
Статическая проверка.
По моментам видно (из эпюры М
(рис. 71) все узлы в равновесии. По Q и N
рассмотрим характерные узлы (рис. 72,а,б). Видим,
что уравнения статики соблюдаются.
Кинематическая проверка.
а)
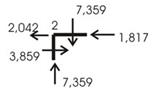
б)
Рис.72
Погрешность составляет 0,04%.
Пример 8.
Построить эпюры внутренних усилий от силового воздействия в раме, изображённой на рис. 73,а, если известно, что изгибная жёсткость поперечных сечений ригелей рамы EJp вдвое больше изгибной жёсткости поперечных сечений её стоек EJс, т.е. EJp : EJс = 2:1.
Решение.
1. Определение степени статической неопределимости рамы по формуле "контуров"
N = 3K–H=32–4=2.
При вычислении n учтено, что шарнир правой стойки рамы, соединяющий в узле три диска, эквивалентен двум простым шарнирам.
2. Выбор основной системы метода сил и её кинематический анализ. Основную систему образуем введением цилиндрических шарниров в верхний и нижний узлы правой стойки рамы, т.е. удалением связей, препятствующих взаимному повороту двух соседних сечений верхнего правого узла рамы и повороту сечения, расположенному близко к правому опорному защемлению рамы. За неизвестные метода сил в нашем случае принимаются усилия в удалённых угловых связях, а именно – изгибающие моменты Х1 и Х2 (рис. 73,б).
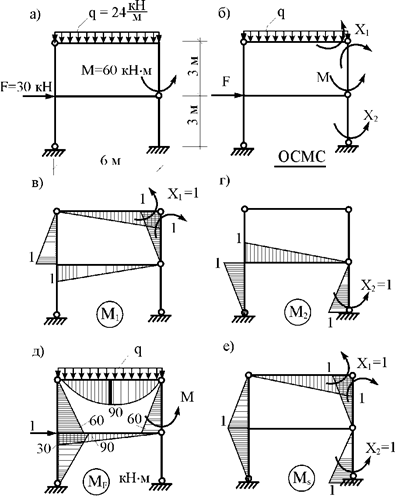
Рис.73
Принятая для расчёта основная система метода сил с кинематической точки зрения имеет простую структуру и геометрически неизменима. Действительно, диск 1 основной системы закрепляется к диску "земля" цилиндрическим шарниром А и связью ab, ось которой не проходит через шарнир А (рис. 74,а). К геометрически неизменяемой структуре AbaС узел В присоединён диадой (двумя связями СВ и аВ).
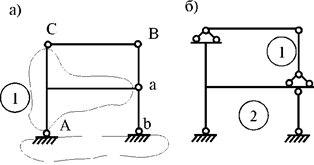
Рис.74
3. Построение эпюр изгибающих моментов в основной системе метода сил от Х1 = 1 (рис. 73,в), Х2 = 1 (рис. 73,г) и заданной нагрузки (рис. 73,д). Эти эпюры читателям предлагается построить самостоятельно, приняв во внимание рабочую схему основной системы (рис. 73,б), на которой показаны её главная и второстепенная части и определён порядок расчёта.
4. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений:
Сопряжение соответствующих эпюр изгибающих моментов будем производить, используя формулу Симпсона и правило Верещагина.
Примем EJp = 2EJ, EJс = EJ (EJ – произвольное число), сохраняя заданное соотношение между изгибными жесткостями поперечных сечений ригелей и стоек рамы.
Читателям рекомендуется тщательно проверить арифметические выражения, записанные ниже для численных значений определённых интегралов формулы Мора.
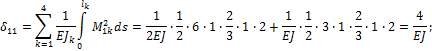
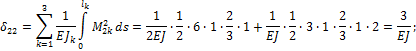
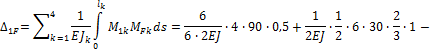
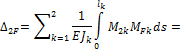
5. Проверка правильности вычисления коэффициентов при неизвестных и грузовых коэффициентов системы канонических уравнений. Суммарная эпюра изгибающих моментов Ms = M1+M2 от Х1 = 1 и Х2 = 1 в основной системе метода сил показана на рис. 73,е.
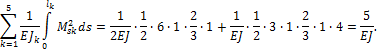
Результат сопряжения эпюры изгибающих моментов Ms саму на себя равен сумме
что подтверждает достоверность вычисления коэффициентов при неизвестных.
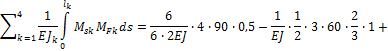
Сумма ранее вычисленных грузовых коэффициентов системы канонических уравнений
совпадает с результатами сопряжения эпюр изгибающих моментов Ms и MF, что свидетельствует о правильности их вычисления.
6. Решение
системы канонических уравнений:
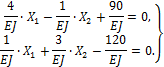
В заданной системе уравнений абсолютное значение жёсткости поперечного сечения стоек рамы EJc = EJ сокращается, т.е. величины усилий в лишних связях Х1 и Х2 и, следовательно, значения внутренних усилий от заданной нагрузки во всех сечениях рамы зависят от относительного значения изгибных жесткостей поперечных сечений элементов рамы. Этот вывод распространяется на любые статически неопределимые стержневые системы при их расчёте на силовое воздействие.
Отсюда получим: Х1 = -13,64 кНм, Х2 = 35,45 кНм. Знак "минус" для числового значения усилия в лишний связи Х1 указывает на обратное направление действия этого усилия по сравнению с предварительно принятым при выборе основной системе метода сил.
7. Определение изгибающих моментов в сечениях заданной рамы и построение соответствующей эпюры.
M = M1X1 + M2X2 + MF.
Ординаты эпюры М1 умножим на –13,64 кНм, а М2 – на 35,45 кНм, затем произведём сложение эпюр М1Х1, М2Х2 и MF (рис. 75). Эпюра изгибающих моментов заданной раме показана рис. 76,а.
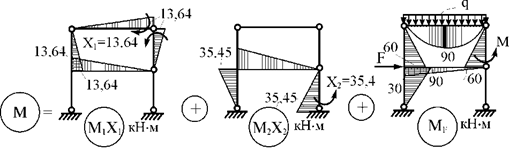
Рис.75
8. Кинематическая проверка. Для этой цели используем суммарную эпюру изгибающих моментов Ms (рис. 73,е)
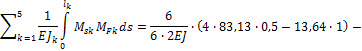
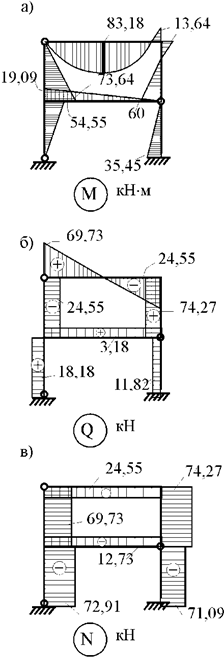
Рис.76
Кинематическая проверка выполнена с нулевой абсолютной погрешностью.
9. Построение эпюр поперечных и продольных сил в заданной раме. Эпюры Q и N для заданной рамы показаны на рис. 76,б,в.
Пример
9.
Дано: статически неопределимая рама (рис.77) и задано соотношение моментов инерции сечений ее элементов I1:I2 = 3:4.
Требуется построить эпюры изгибающих моментов М, поперечных сил Q и продольных сил N.
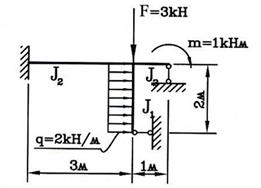
Рис.77
Решение.
1. Определяют степень статической неопределимости рамы.
n= 5 – 3=2,
где 5 – число независимых опорных реакций, 3 – число уравнений статики на плоскости.
2. Основная система показана на рис.78
Рис.78
В рассматриваемой задаче возможны и другие варианты основной системы, показанные на рис.79.
Рис.79
В выбранной консольной основной системе (рис.78) грузовая и единичные эпюры моментов могут быть построены без вычисления опорных реакций, только на основании одного лишь определения изгибающего момента в сечении.
Если основная система балочного или арочного типа, то необходимо привести все расчеты, связанные с построением эпюр.
3. Канонические уравнения:
Здесь и 
- неизвестные усилия (реакции) в отброшенных
связях.
4. Определение коэффициентов и грузовых членов канонических уравнений.
4.1. На рисунках 80 и 81 показаны единичные эпюры моментов М1 и М2 и эпюра изгибающих моментов от заданной нагрузки МР (рис.82).
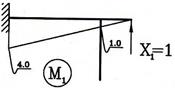
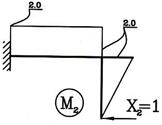
Рис.80
Рис.81
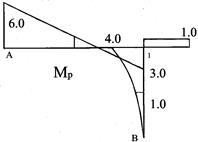
Рис.82
4.2.
Вычисление коэффициентов и свободных (грузовых) членов 
.
Так как
элементы рамы имеют разную жесткость на изгиб, то при вычислениях вводят
условную жесткость 
,
учитывая заданное соотношение моментов инерции 
Жесткость вертикального элемента примем равной
,
а ригеля - 
.
Раму разбивают на участки, на которых перемножаемые эпюры изображены прямыми линиями или очерчены по параболе.
Для определения перемещений применим способ Верещагина.
(Точное положение центра тяжести трапеции на участке А1 определять не нужно, так как где бы он не находился внутри площади трапеции, ордината под ним в эпюре М2 будет постоянна).
Знак минус перед произведением объясняется тем, что площадь трапеции в эпюре М1 и ордината под ее центром тяжести в эпюре М2 лежат по разные стороны элемента А1.
5. Решают систему канонических уравнений, находят неизвестные усилия Xi.
5,33X1 –3,75X2 –4,625 = 0
-3,75X1 +3,88X2+0,9166=0
X1=2,18
X2=1,865.
6. Строят
окончательную эпюру М=МР + М1
X1 +М2 X2.
6.1. Вначале строят исправленные эпюры М1X1 и М2X2 (рис.83)
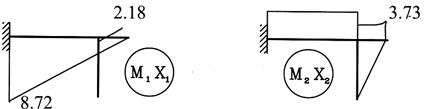
Рис.83
Если найденное усилие Xi получилось со знаком минус, то соответствующая исправленная эпюра должна быть построена на противоположных, чем эпюра Мi, сторонах элементов рамы.
6.2. Окончательная эпюра моментов М получается
аккуратным сложением (по точкам)
исправленных и грузовой эпюр
(рис.84).
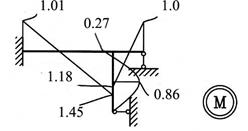
Рис.84
7. Проверка эпюры М.
На рис.85 показана суммарная единичная эпюра МS= М1+М2
Рис.85
Перемножаем эпюры M и MS
Ошибка счета составляет всего
8. Строят эпюру поперечных сил Q.
Эпюра поперечных сил показана на рис. 86
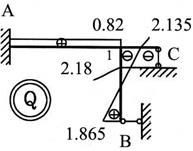
Рис.86
9. Строят эпюру продольных сил N .
Продольные силы находят из равновесия узлов рамы. Вырежем элемент рамы у опоры С (рис.87)
Рис.87
Вырежем узел 1 (рис.88)
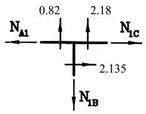
Рис.88
Эпюра N показана на рис.89
Рис.89
10. Проверка общего равновесия рамы.
Раму отрезают от опор и в местах разрезов прикладывают значения N и Q с полученных эпюр. Эти усилия должны находиться в равновесии с действующей на раму нагрузкой (рис.90).
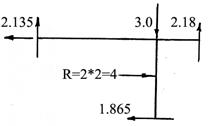
Рис.90
Пример
10.
Пусть требуется провести расчет плоской рамы (рис. 91, a) методом сил в следующей последовательности:
1. Определение степени статической неопределимости;
2. Выбор основной системы;
3. Составление системы канонических уравнений;
4. Вычисление коэффициентов канонических уравнений;
5. Проверка правильности подсчета коэффициентов канонических уравнений;
6. Решение системы канонических уравнений и проверка ее правильности;
7. Построение окончательной эпюры изгибающих моментов Mок;
8. Проверка правильности построения эпюры Mок и построение эпюры Q(z);
9. Построение эпюры N;
10. Статическая и деформационная проверка рамы в целом.
Решение.
1. Определение степени
статической неопределимости
Подсчитаем степень статической неопределимости системы. Количество опорных стержней 5, количество уравнений равновесия 3, то отсюда n=5-3=2, следовательно, система дважды статически неопределима, или, другими словами, имеет две лишние связи.
2. Выбор
основной системы
Известно, что основная система определяется из заданной путем отбрасывания лишних связей и приложением соответствующих усилий, возникающих в отброшенных связях в заданной системе. При этом основная система должна быть статически определимой и геометрически неизменяемой.
Рис. 91
Сравнивая три варианта основных систем (рис.91, б -г) приходим к выводу, что наиболее целесообразно в качестве основной системы выбрать I-ый вариант (рис. 91, б), так как в этом случае:
- не требуется предварительное вычисление опорных реакций;
- эпюры изгибающих моментов, построенные в этой схеме от воздействия на нее каждого из усилий Х1 = 1, Х2 = 1, Р и q, будут распространены на меньшем количестве участков системы и представлены простейшими геометрическими фигурами. Это значительно облегчает процесс определения коэффициентов канонических уравнений.
3. Составление
системы канонических уравнений
Канонические уравнения, необходимые для решения статически неопределимых задач, представляют собой уравнения совместности деформаций. Число их всегда равно степени статической неопределимости. Физический смысл каждого из канонических уравнений, как было указано выше, состоит в том, что суммарное перемещение по направлению усилий Xi от всех действующих в основной системе силовых факторов, включая и неизвестные, равно 0, так как в действительности в этих направлениях стоят связи, препятствующие возникновению перемещений по направлению этих неизвестных.
Для рассматриваемого случая канонические уравнения имеют вид:
4. Вычисление
коэффициентов канонических уравнений
Так как все коэффициенты канонических уравнений представляют собой перемещения, то для их вычисления вначале строят единичные и грузовые эпюры изгибающих моментов в основной системе. Затем по формуле Мора с применением готовых формул или правила Верещагина с использованием табл.2 определим их значения.
Эпюры изгибающих моментов, построенные в основной системе от воздействия на нее каждого в отдельности усилия X1 = 1; X2 = 1; P и q, показаны на рис. 91, д - 91, з.
Исходя из единичных и грузовых эпюр определяем коэффициенты канонических уравнений:
5. Проверка
правильности подсчета коэффициентов
Правильность расчета коэффициентов канонических уравнений осуществляется путем универсальных проверок, при этом должны выполняться следующие условия:
где 
- сумма всех найденных главных и побочных коэффициентов:
- величина,
полученная в результате умножения единичной суммарной эпюры Må
на себя:
- величина,
определяемая сложением значений, полученных в результате умножения эпюры на эпюру MP
и эпюры на эпюру Mq; k - количество участков
эпюры.
Эпюра 
(рис.91, и)
строится в основной системе от одновременного воздействия на нее всех
неизвестных единичных усилий (X1 = 1; X2 = 1), т.е.
путем сложения единичных эпюр M1
и M2:
В нашем
случае
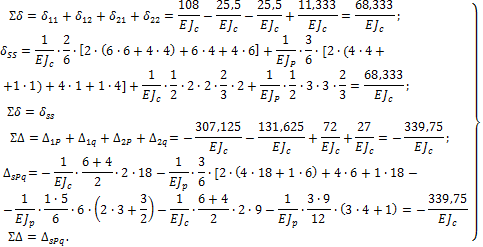
Таким образом, оба условия удовлетворяются. Следовательно, коэффициенты канонических уравнений рассчитаны верно.
6. Решение системы канонических
уравнений и проверка ее правильности
Подставив в систему уравнений значения коэффициентов канонических уравнений, получим:
Решив эту систему уравнений, найдем значения неизвестных:
X1 = 4,267 кН; X2 = 0,865 кН.
Правильность вычисления неизвестных проверим путем подстановки найденных значений X1 и X2 в исходные уравнения:
108 ∙ 4,267 - 25,5 ∙ 0,865 - 438,750 = 460,836 - 460,808 ≈ 0;
-25,5 ∙ 4,267 + 11,333 ∙ 0,865 + 99 = -108,808 + 108,803 ≈ 0.
7. Построение окончательной эпюры
изгибающих моментов Mок
Ординаты окончательной эпюры изгибающих моментов Mок в характерных сечениях заданной системы целесообразно подсчитать в табличной форме (табл.3), предварительно пронумеровав все характерные сечения и задавшись правилом знаков изгибающих моментов (рис.92, б).
Окончательную эпюру изгибающих моментов Mок для заданной системы строим в соответствии с принципом независимости действия сил путем сложения «исправленных» эпюр M1 X1 и M2 X2 с грузовыми эпюрами MP и Mq , которые построены в основной системе:
Mок = M1 X1 + M2 X2 + MP + Mq .
«Исправленные» эпюры изгибающих моментов M1 X1 и M2 X2 строим путем умножения всех ординат единичных эпюр M1 и M2 , соответственно, на значения X1 и X2 с учетом их знака. Построенные таким образом эпюры M1 X1 и M2 X2 приведены на рис. 91, к и рис. 92, а.
Таблица 3
|
Номер |
M1X1, |
M2X2, |
MP, |
Mq, |
Mок, |
|
0 |
25,602 |
0 |
-9,0 |
-18,0 |
-1,398 |
|
1 |
25,602 |
-1,73 |
-9,0 |
-18,0 |
-3,128 |
|
2 |
25,602 |
-1,73 |
-9,0 |
-18,0 |
-3,128 |
|
3 |
12,801 |
-1,73 |
0 |
-6,0 |
5,071 |
|
4 |
0 |
-1,73 |
0 |
0 |
-1,730 |
|
5 |
0 |
0 |
0 |
0 |
0 |
|
6 |
12,801 |
0 |
0 |
-6.0 |
6,801 |
|
7 |
6,400 |
0 |
0 |
0 |
6,400 |
|
8 |
6,400 |
0 |
0 |
0 |
6,400 |
|
9 |
0 |
0 |
0 |
0 |
0 |
Так как на участке 2-3 эпюра Mок (рис. 92, в) криволинейна, то для уточнения ее очертания необходимо найти экстремальное значение изгибающего момента. Для этого рассмотрим элемент 2-3, вырезанный из статически неопределимой системы. На этот ригель действует равномерно распределенная нагрузка q = 2 кН/м и два опорных момента М2 = -3,128 кНм и М3 = 5,071 кНм (табл.3).
Расчетная схема этого элемента показана на рис. 92, г. Вначале вычислим опорные реакции, составив уравнения равновесия:
откуда R2 = 5,733 кН и R3 = 0,267 кН.
Проверим правильность вычисления опорных реакций, составив уравнения равновесия:
Определим координату
сечения, в котором Q = 0, а 
,
использовав следующую дифференциальную зависимость:
Откуда
Тогда для этого сечения получим:
Рис. 92
По найденным значениям ординат строим окончательную эпюру изгибающих моментов Мок для заданной рамы (рис. 92, в).
8. Проверка
правильности построения эпюр Мок и Q(z)
Для
проведения статической проверки вырезаем жесткие узлы рамы кроме опорных,
прикладываем все действующие в них моменты и проверяем условия равновесия 
В нашем примере вырежем узлы B и С (рис. 92, д) и проверим их равновесие.
Узел В: 
Узел С: 
Условия равновесия узлов B и С выполняются. Выполнение условия равновесия узлов является необходимым, но недостаточным. Достаточным условием правильности определения Мок является выполнение деформационной проверки заданной системы с применением эпюры Мок, суть которого заключается в доказательстве отсутствия перемещения в точках и по направлению каждой отброшенной связи, т.е.:
Эта проверка хотя и не имеет физического смысла, так как складываются различные по направлению перемещения, но она дает возможность доказать правильность построения Мок во всех сечениях заданной системы.
Для удобства вычислений целесообразно расчленить криволинейную эпюру Мок на участке рамы 2-3 (рис. 92, в) на трапецеидальную и параболическую (подобно приведенному выше на рис. 32). Тогда
Ординаты эпюры Q(z) определяем используя зависимость Q(z)=dM(z)/dz или записывая в конечных разностях:
где 
- поперечная
сила в сечениях с координатой z по
длине участка, имеющего расчетную схему в виде простой двухопорной
балки, загруженной заданной внешней нагрузкой (рис.92, г).
Участок 0-1. На этом участке
внешняя нагрузка отсутствует, поэтому 
,
и 
определяем по формуле (а):
Участок 2-3. В этом случае при наличии нагрузки q = 2 кН/м имеем:
откуда при z = 0: Q2 = 5,733 кН;
при z = l = 3 м: Q3 = 5,733 - 6= -0,267 кН.
Участок 4-5. 
Участок 6-7. 
Участок 8-9.
По найденным значениям ординат строим эпюру Q (рис.92, е).
9. Построение
эпюры N
Ординаты
эпюры продольных сил определяем из условий равновесия 
и 
узлов рамы, вырезанных из эпюры Q. При этом отрицательную поперечную
силу направляем так, чтобы она вращала вырезанный узел против хода часовой
стрелки, а положительную - по ходу часовой стрелки. Нормальные силы направляем
от узла, т.е. предполагаем, что стойка и ригель растянуты.
Вырезав узел В (рис. 92, ж), составим уравнения равновесия:
Знак «минус» говорит о том, что направления продольных усилий ригеля и стойки были приняты неверно. Поэтому в действительности ригель и стойка не работают на растяжение, а на сжатие.
Из рассмотрения равновесия узла С (рис.92, з) следует:
По вычисленным значениям ординат для каждого участка строим эпюру N (рис.92, и).
10. Статическая проверка рамы в целом
Статическая
проверка рамы в целом производится для подтверждения правильности построения
эпюр Q, N и Мок . Она заключается в проверке равновесия
рамы в целом или любой отсеченной ее части, т.е. проверке удовлетворения
условий равновесия ;
;
под воздействием внешних нагрузок и внутренних
усилий, возникающих в местах проведенных сечений.
Для выполнения этой проверки отсечем заданную раму от всех опор и заменим их действие возникающими в этих сечениях внутренними усилиями Q, N и M (рис.92, к), значения которых определяются по эпюрам Q, N и Mок . Направление всех внутренних усилий при этом должно соответствовать их знаку. Следовательно:
Уравнения равновесия удовлетворяются, cледовательно, рама рассчитана верно.
Использование свойств симметрии при раскрытии статической неопределимости
Использование
метода сил для расчета систем с высокой степенью статической неопределимости
связано с решением совместной системы большого количества линейных уравнений.
Даже самый экономичных метод решения таких систем – алгоритм Гаусса –
требует 
вычислительных
операций (где n – число уравнений,
т.е. степень статической неопределимости системы), при условии, что все
коэффициенты системы отличны от нуля. В связи с этим нужно стремиться так выбрать основную систему, чтобы возможно большее число
побочных единичных перемещений 
и
свободных членов обратилось
в ноль.
Основным средством для достижения этой цели является использование симметрии. Стержневая система является симметричной, если симметричны не только оси и опорные закрепления (геометрическая симметрия), но и жесткости (упругая симметрия). При этом внешняя нагрузка может быть и несимметричной.
При выборе основной системы лишние неизвестные следует выбирать в виде симметричных и обратно симметричных усилий. Симметричные неизвестные создают симметричные эпюры моментов, а обратно симметричные неизвестные – кососимметричные эпюры. Такие эпюры обладают свойством взаимной ортогональности, т.е. результат их перемножения равен нулю:
Ортогонализация эпюр может достигаться различными способами:
1) выбор симметричной основной системы;
2) выбор симметричных и обратносимметричных неизвестных;
3) группировка неизвестных;
4) устройство жестких консолей (способ упругого центра);
5) использование статически неопределимой основной системы;
6) разложение произвольной нагрузки на симметричную и обратносимметричную составляющие.
Рассмотрим раму, имеющую ось геометрической симметрии (рис.93, а). Заменим внешнюю нагрузку ей статически эквивалентной, такой, что она представляет сумму симметричной (рис.19, б) и кососимметричной (рис.19, в) нагрузок относительно оси геометрической симметрии.
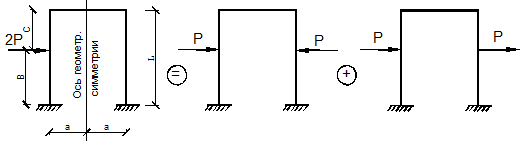
а)
б)
в)
Рис. 93
Аналогично можно классифицировать внутренние силовые факторы в произвольном сечении стержневой системы (рис.94).
Изгибающие моменты МХ, МУ, нормальная сила N являются зеркальным отражением друг друга относительно плоскости поперечного сечения. Эти внутренние силовые факторы назовём симметричными. Остальные (перерезывающие силы Qx, Qy и крутящий момент Мz ) назовём антисимметричными или кососимметричными силовыми факторами.
Рис. 94
Докажем теперь положение:
у геометрически симметричной рамы в плоскости симметрии при симметричной внешней нагрузке обращаются в нуль кососимметричные внутренние силовые факторы, а при кососимметричной внешней нагрузке – симметричные силовые факторы (рис.95).
Канонические уравнения метода сил для изображённой на рис.93 трижды статически неопределимой рамы имеют вид
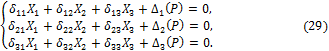
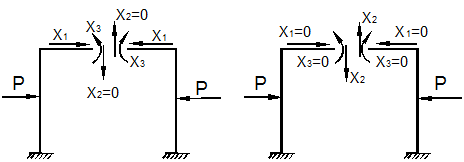
а)
б)
Рис. 95
На рис. 96 приведены эпюры изгибающих моментов от единичных сил.
На основании этих эпюр находим:
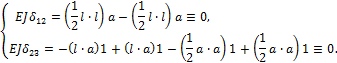
а)
б)
в)
Рис. 96
Следовательно, канонические уравнения (29) принимают вид
На рис. 23 приведены эпюры моментов от внешних симметричной (рис.97, а) и кососимметричной (рис.97, б) нагрузок.
В первом случае симметричной внешней нагрузки имеем:
а)
б)
Рис. 97
Из (30) следует Х2 = 0, т.е. при симметричной внешней нагрузке обращается в нуль кососимметричный силовой фактор (перерезывающая сила), что и требовалось доказать.
Во втором случае кососимметричной внешней нагрузки имеем:
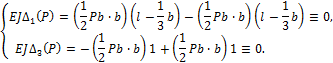
Канонические
уравнения (30) принимают вид
Т.к. определитель системы двух первых уравнений (31)
то 
,
что и требовалось доказать.
Рассмотрим другой пример.
Воспользуемся симметрией рамы на рис. 98,а и разложим внешнюю нагрузку на симметричную (рис. 98,б) и кососимметричную (рис. 98,в).
Рис. 98
В этом случае, несмотря на то что раму приходится рассчитывать дважды, выбор основной системы, показанной на рис. 99,а дает значительный выигрыш в вычислениях.
Рис. 99
Канонические уравнения будут:
Во всех трех единичных состояниях построим эпюры моментов (рис. 99, б, в, г). Из них две эпюры (рис. 99, б, г) – симметричные, а одна (рис. 99, в) – кососимметричная. Симметричная (с) и кососимметричная (кс) эпюры взаимно-ортогональны и их “произведение” равно нулю:
Поэтому некоторые коэффициенты системы канонических уравнений
обращаются в нуль: 
и 
,
а система канонических уравнений распадается на две независимые системы:
Таким образом, при расчете симметричной рамы некоторые коэффициенты можно не вычислять, а решение большой системы канонических уравнений заменить решением двух систем уравнений значительно меньших размеров.
а) Расчет на симметричную нагрузку
Так как эпюра изгибающих
моментов при действии симметричной нагрузки также является симметричной
(рис. 8.2 д), она ортогональна кососимметричной эпюре 
.
Следовательно, 
. Поэтому, как следует из уравнения (2), X2=0. Таким образом, при
симметричной нагрузке кососимметричная неизвестная равна нулю. В этом случае
эпюра изгибающих моментов будет строиться по формуле
Она, как сумма симметричных эпюр, будет симметричной. Тогда эпюра Q будет кососимметричной, а эпюра N будет симметричной.
б) Расчет на кососимметричную нагрузку
В этом случае эпюра изгибающих
моментов кососимметрична (рис. 99,е)
и ортогональна симметричным эпюрам и 
.
Следовательно, 
,
и, как следует из системы уравнений (1), X1=X3=0.
Таким образом, при кососимметричной нагрузке все симметричные неизвестные равны
нулю. Поэтому эпюра изгибающих моментов строится по формуле
Тогда она и эпюра N будут кососимметричными, а эпюра Q будет симметричной.
Окончательно будет
Группировка неизвестных
Если при расчете симметричной рамы (рис. 100,а) выбрана обычная основная система (рис. 100,б), то все коэффициенты канонических уравнений
будут отличаться от нуля.
Рис. 100
Если же неизвестные группировать по формулам
X1=Y1 +Y2 ,
X2=Y1 – Y2 ,
что соответствует основной
системе на рис.100,д, то единичные
эпюры (рис. 100,е, ж) будут
ортогональными (
),
и канонические уравнения распадутся на два независимых уравнения:
Как видим, при группировке неизвестных отдельные коэффициенты обращаются в нуль и нет необходимости их вычисления. С другой стороны, распадение системы канонических уравнений на две независимые системы уравнений упрощает их решение. Поэтому группировка неизвестных позволяет существенно уменьшить объем вычислений.
Полученные результаты могут быть распространены на пространственные стержневые системы.
Матричная форма метода сил
При ручном счете возникают серьезные вычислительные трудности уже при степени статической неопределимости три и выше. Кроме этого, возрастает вероятность ошибок при определении грузовых и единичных перемещений, решении систем канонических уравнений и т.д. С развитием ЭВМ появилась возможность некоторые рутинные и громоздкие вычислительные операции переложить на электронную машину. Однако, ряд операций, связанных с подготовкой задачи, приходится решать вручную. Речь идет о построении эпюр грузовых и единичных изгибающих моментов. Численные значения грузовых и единичных моментов, длины участков, жесткости элементов конструкции можно специальным образом обработать и занести в память ЭВМ. Все дальнейшие расчеты ЭВМ производит без участия человека по специально разработанной программе. В результате этих расчетов ЭВМ выдает на печать информацию о распределении внутренних силовых факторов.
Сформулируем матричную запись системы канонических уравнений. Для этого сформируем несколько матриц, в число которых входят матрица-столбец “лишних” неизвестных, матрица-столбец свободных членов, матрица единичных коэффициентов.
Матрица-столбец
“лишних” неизвестных X,
матрица-столбец свободных членов 
и матрица единичных коэффициентов A имеют соответственно вид:
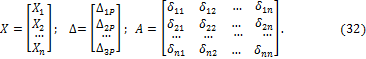
Матричная запись системы канонической системы уравнений с учетом (32) принимает вид:
Решение матричного уравнения (33) относительно вектора
“лишних” неизвестных принимает вид:
где матрицу свободных членов можно определить с помощью матричного уравнения:
Здесь B - матрица податливости. Для j -го
элемента системы матрица податливости имеет вид:
Матрицу единичных коэффициентов найдем из матричного
уравнения:
С учетом (35) и (36) матричная форма системы
канонических уравнений имеет вид:
Матричное уравнение для определения суммарных
изгибающих моментов записывается в виде:
Сформулируем порядок решения статически неопределимых
систем методом сил матричным методом:
1. Разбиваем статически неопределимую систему на участки (рис.101), выбираем точку наблюдения, вводим положительные и отрицательные стороны и проставляем слева направо “характерные” сечения на каждом участке.
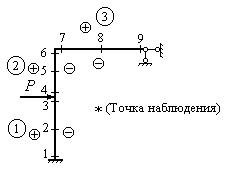
Рис.101. Подготовка задачи к решению
2. Определяем степень статической неопределимости системы.
3. Выбираем основную систему.
4. Изображаем эквивалентную систему.
5. Строим
эпюру грузовых моментов .
6. Изображаем
единичные состояния системы и строим эпюры единичных моментов .
7. Формируем матрицу грузовых моментов:
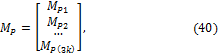
где k - число участков.
8. Формируем матрицы единичных моментов:
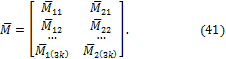
9. Формируем матрицу податливости B:
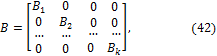
где j-ый
элемент матрицы податливости 
определяется из выражения (36).
10. Вводим
сформированные матрицы в определенной последовательности в память ЭВМ.
Электронная машина вычисляет значения всех “лишних” неизвестных и суммарные
изгибающие моменты 
и поперечные силы 
в каждом из “характерных” сечений и выдает на
печать в виде соответствующих векторов. На печать выводится также вся вводимая
информация.
11. По
векторам и строим соответствующие суммарные эпюры.
12. Методом
вырезания узлов строим эпюру продольных сил 
.
Определение перемещений в статически неопределимых стержневых системах
Когда была рассмотрена теория определения перемещений, то в качестве принятых допущений не было никаких ограничений на тип конструкций с точки зрения статической определимости. Тогда полученные формулы для определения перемещения (полный или неполный интеграл Мора) справедливы и для статически неопределимых стержневых систем.
Очевидный путь определения перемещений заключается в том, что для применения формул вычисления перемещения необходимо дважды раскрыть статическую неопределимость – на действие заданной нагрузки и на единичное воздействие, приложенное в сечение, перемещение которого следует найти. Очевидна и трудоемкость определения перемещений при реализации такого подхода.
А следует ли и во втором случае, т.е. при приложении единичной нагрузки также раскрывать статическую неопределимость?
При раскрытии статической неопределимости от действия заданной нагрузки мы перешли к основной системе метода сил – статически определимой системе с наложенными дополнительными условиями в форме канонических уравнений. По сути, мы переходим к расчету статически определимой системы под действием известной внешней нагрузкой и найденными из решения канонических уравнений усилиями. Тогда, во втором состоянии, мы вправе рассмотреть любую статически определимую систему, получаемую из заданной путем перехода к основной системе метода сил. Разумеется, что для второго состояния (нагружение единичной нагрузкой) основную систему метода сил следует выбирать такую, чтобы эпюра изгибающих моментов строилась бы проще и имела минимальное число ненулевых участков с эпюрой от заданной нагрузки.
Обобщая, можем утверждать, что для определения перемещения в статически неопределимой системе достаточно раскрыть статическую неопределимость для любого случая нагружения, наиболее простого, а таким является второе состояние, а от заданной нагрузки рассмотреть статически определимую систему.
Расчет статически неопределимых плоскопространственных систем методом сил
Пример 11.
Для заданной плоскопространственной рамы (рис.102) требуется:
1) раскрыть статическую неопределимость,
2) построить эпюры изгибающих и крутящих моментов,
3) определить коэффициент запаса по текучести, используя гипотезу энергии формоизменения.
Для расчета
принять: F = 1 кН; l = 0,4 м; G=0,4E, 
МПа ; 
мм, сечение представляет собой тонкостенный
замкнутый профиль (рис.103).
Рис.102
Рис.103
Решение.
Плоскопространственными называются системы, плоские в геометрическом отношении, но нагруженные силовыми факторами, перпендикулярными к плоскости рамы.
Особенностью этих систем является то, что внутренние силовые факторы во всех поперечных сечениях рамы, лежащие в плоскости рамы равны нулю.
Заданная плоскопространственная рама шесть раз статически
неопределима.
Для решения задачи разрежем раму по оси косой симметрии. В месте разреза возникает шесть внутренних силовых факторов:
Х1- поперечная сила, лежащая в вертикальной плоскости
Х2- поперечная сила, действующая в горизонтальной плоскости (лежит в плоскости рамы)
Х3- крутящий момент
Х4- продольная сила (лежит в плоскости рамы)
Х5- изгибающий момент, действующий в горизонтальной плоскости (лежит в плоскости рамы)
Х6- изгибающий момент, действующий в вертикальной
плоскости.
Чтобы не затенять рисунок, факторы х4; x5 и х6, действующие на левую половину рамы, вынести на отдельную схему.
Рис.104
Рис.105
В соответствии с особенностями плоскопространственной рамы X2=0; X4=0; X5=0.
Следовательно, расчетная схема приобретает вид:
Рис.106
Для полученной расчетной схемы записываем систему канонических уравнений и строим эпюры изгибающих и крутящих моментов от действия внешних нагрузок и усилий: X1=1; X3=1 и X6=1.
Рис.107
Рис.108
Определяем коэффициенты, входящие в систему уравнений. Для их определения необходимо знать моменты инерции заданного сечения при изгибе и кручении.
Рис.109
Момент инерции при изгибе определяется как:
В остальных
случаях:
В нашем
случае: H=21
; B=21.
Момент инерции при кручении определяется как
где Ао=(B-)(H-)
– площадь сечения по серединному контуру.
S=2[(B-)+(H-)]
– длина периметра серединного контура.
В нашем случае:
Из последнего уравнения системы получаем, что х6 – изгибающий момент, являющийся симметричным фактором, при кососимметричном нагружении рамы оказался равным 0.
Таким образом, для плоскопространственных рам, как и для плоских рам справедливо свойство симметрии и косой симметрии.
Решаем систему, состоящую из двух первых уравнений, сократив все коэффициенты на общий множитель (2/(EIx)).
Получаем,
что х1=
- 0,46F
Строим эпюры изгибающих моментов от истинных значений х1 и х3.
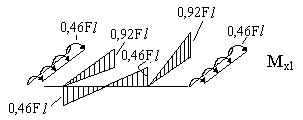
Рис.110
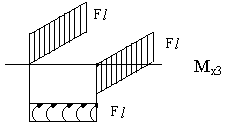
Рис.111
Строим суммарные эпюры изгибающих и крутящих моментов.
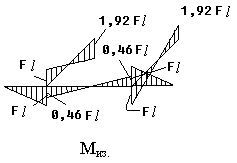
Рис.112
Рис.113
Наиболее опасными будут сечения в заделке.
Рассмотрим сечение в левой заделке. Т.к. эпюры изгибающих моментов строятся на сжатых волокнах, то низ сечения будет испытывать нормальные напряжения сжатия, а верх – растяжения (см. эпюру).
Рис.114
Миз=1,92Fl=1,9211030,4103=0,768106
(Hмм)
Касательные напряжения по толщине стенки постоянны и одинаковы во всех точках сечения.
T=0,54Fl=0,5411030,4103=0,216106
(Нмм)
Определяем
эквивалентные напряжения.
Определим коэффициент запаса по текучести
Пример 12.
Плоскопространственная рама, изготовлена из прутка
квадратного поперечного сечения (а=20
мм), нагружена так, как показано на рисунке 115. Определить допускаемую
нагрузку, если материал – сталь Ст
3 (
Мпа) и характерный размер конструкции l = 0,2 м.
Рис.115
Решение.
Для определения допускаемой нагрузки необходимо проанализировать напряженное состояние материала конструкции в наиболее нагруженном сечении. Построение эпюр внутренних силовых факторов невозможно без раскрытия статической неопределимости. Заданная рама три раза статически неопределима. (В заделке В возникает 6 реакций связей; на опоре С – две реакции; на опоре Д – одна) уравнений статики в пространстве – 6).
Отбрасывая “лишние” связи, получаем следующую основную систему (рис.116)
Рис.116
Превращаем основную систему в систему, эквивалентную заданной (рис.117) и записываем систему канонических уравнений метода сил.
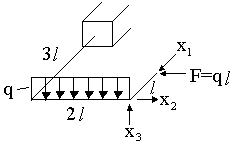
Рис.117
Для определения коэффициентов, входящих в эту систему, строим эпюры изгибающих моментов от внешних нагрузок и сил х1; x2 ; х3; равны 1.
При построении грузовой эпюры используем метод независимости действия сил (рис.118 и рис.119).
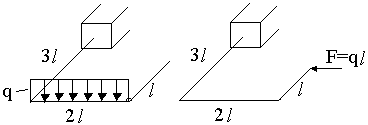
Рис.118
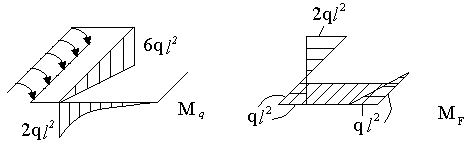
Рис.119
Эпюры изгибающих моментов от единичных нагрузок имеют вид (рис.120):
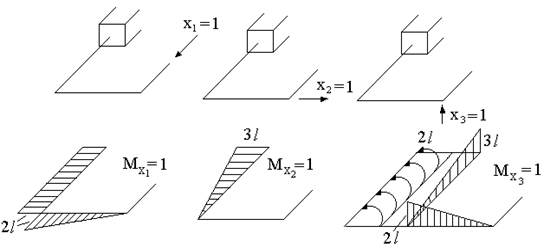
Рис.120
Определяем коэффициенты системы канонических уравнений
Для квадратного сечения:
Для стали 
Тогда
Подставляем найденные значения в систему канонических уравнений и
сокращаем на общий множитель EJx
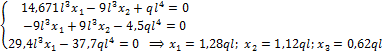
Перестраиваем эпюры от единичных нагрузок с учетом найденных значений усилий x (рис.121).
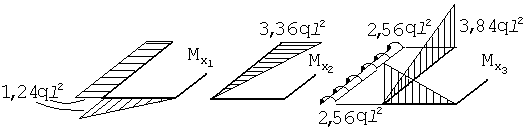
Рис.121
И строим суммарную эпюру изгибающих моментов (рис.122).
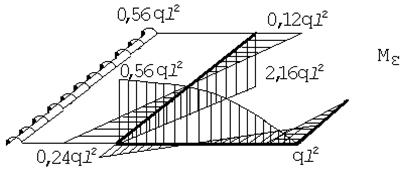
Рис.122
Наиболее опасным является сечение в заделке (рис.123).
Рис.123
Наиболее опасными будут точки 1 и 2, в которых возникают наибольшие напряжения.
Точка 1 (рис.124):
Рис.124
Так как гипотеза, по которой необходимо определить эквивалентные напряжения, не оговорена, принимаем гипотезу наибольших касательных напряжений.
Точка 2 (рис.125):
Рис.125
Напряженное состояние линейно. Поэтому
Точка 1 более
опасна, поэтому для определения допускаемой нагрузки используем 
.
Условия прочности.
Вопросы для самопроверки
- Чем определяется число степеней свободы системы? Зависит ли это число от выбора системы координат?
- Сколько степеней свободы имеет стержень на плоскости и в пространстве?
- Что такое связь? Как изменяется степень свободы системы при наложении на нее одной связи?
- Сколько связей накладывают на стержень катковая опора, шарнирная опора, заделка?
- Что такое реакции связей? Как они направлены?
- Что такое кинематически неизменяемые и изменяемые системы?
- Какой (кинематически изменяемой или неизменяемой) является система, на которую наложены только необходимые связи? Что такое лишние связи? Можно ли произвольно делить связи на необходимые и лишние?
- Что называют статически определимыми и статически неопределимыми системами?
- Что называется степенью статической неопределимости системы?
- Как определяется степень статической неопределимости?
- Обязательно ли отбрасывать все лишние связи при определении степени статической неопределимости системы?
- Сколько рассечений нужно сделать в плоском замкнутом контуре, чтобы он стал статически определимым?
- Чем принципиально отличаются статически неопределимая балка от статически определимой?
- Какие методы могут быть использованы для расчета статически неопределимых балок?
- Как решают простейшие статически неопределимые балки?
- В каком случае балка является статически неопределимой?
- Какие условия равновесия обычно записывают для определения опорных реакций?
- Какое дополнительное уравнение к трем основным уравнениям статики добавляет врезка в сечении балки шарнира?
- Какой порядок расчета используется при решении статически неопределимых балок?
- Какие плоские рамы считаются статически неопределимыми?
- Какой метод расчета наиболее предпочтителен для расчета рам?
- Как определяется степень статической неопределимости рамы?
- Для чего и как проводятся деформационная проверка при решении статически неопределимых балок?
- Что представляет собой основная система?
- В чём заключается выбор основной системы?
- Как получить из статически неопределимой системы основную? Однозначен ли выбор основной системы?
- Почему основная система статически определима?
- Что такое эквивалентная система? В чем принципиальное ее отличие от исходной?
- При каком условии эквивалентная система будет деформироваться так же, как и исходная?
- Что понимается под выражением «каноническое уравнение» метода сил?
- Что выражает каждое из канонических уравнений?
- Как составляют канонические уравнения метода сил?
- Сколько канонических уравнений нужно записать для n раз статически неопределимой системы и почему?
- Каков
физический смысл произведений 
?
- Каков физический смысл произведений коэффициентов канонических уравнений на неизвестные силы?
- Какие перемещения называют главными и побочными. Какими свойствами они обладают?
- В каком порядке производится расчёт статически неопределимых систем?
- Перемножением каких эпюр определяют коэффициенты и свободные члены системы канонических уравнений?
- Где находятся точки центров тяжести простейших фигур и как вычисляются величины их площадей?
- Как определяются значения неизвестных Хi?
- Какими приёмами можно построить окончательную (суммарную) эпюру изгибающих моментов?
- Как производится статическая проверка правильности раскрытия статической неопределимости системы?
- Как проводят деформационную проверку правильности построения окончательной эпюры М статически неопределимой системы?
- Как производится определение перемещений в статически неопределимых системах?
- Какие системы называют геометрически неизменяемыми?
- Объясните смысловую сторону метода сил?
- Какой порядок расчета принят при решении статически неопределимых рам?
- Какие конструкции называют зеркально симметричными? Кососимметричными?
- Какие нагрузки называют зеркально симметричными? Кососимметричными?
- Сколько шарниров должна содержать плоская замкнутая рама, чтобы быть статически определимой?
- Какому условию должны удовлетворять нагрузки для применения метода сечений?
- Можно ли использовать метод сил при решении пространственных статически неопределимых рам?
- Как используют свойство симметрии рам при их решении?
- Какие проверки используются при решении рам?
- Как называется проверка правильности вычисления коэффициентов и свободных членов какнонических уравнений?
- Какие эпюры строятся для статически неопределимых рам?
- Какие эпюры строятся для статически неопределимых кривых стержней?
- Какие эпюры строятся для статически неопределимых пространственных систем?
- Определить с помощью формулы n=3K-Ш степень статической неопределимости конструкции, изображенной на рисунке:
-
Определить реакцию в сечении
В рамы, изображенной на
рисунке.
-
Определить опорный момент в сечении А рамы, изображенной
на рисунке.
- Определить внутренние усилия и
перемещения консольной балки прямоугольного сечения, нагруженной силой P и
имеющей удельный вес 
.
Модуль Юнга равен E, размеры указаны на рисунке.
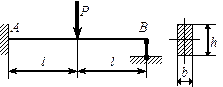
- Определить внутренние усилия и перемещения консольной балки прямоугольного сечения, нагруженной консольной силой P. Модуль Юнга E, размеры указаны на рисунке.
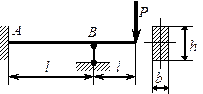
- Определить внутренние усилия и
перемещения ненагруженной балки AB с заделанными концами,
если правая заделка будет повёрнута вокруг точки B на угол 
.
Модуль Юнга равен E. Размеры указаны на рисунке.
- Балка AB заделана по концам и не несёт нагрузки. Правая заделка B переместилась поступательно вниз на величину .
Определить внутренние усилия и перемещения. Модуль Юнга равен E. Размеры указаны на рисунке.
- Для балки, изображенной на рисунке, определить опорный момент (в кНм) в сечении А (абсолютную величину).
- Определить изгибающий момент на промежуточной опоре В для балки, изображенной на рисунке.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
