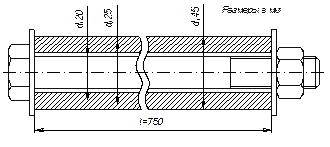Лекция
2 (продолжение). Задачи для самостоятельного
решения
Содержание
Расчет статически определимых стержней
на растяжение-сжатие
Расчет статически неопределимых
стержней при растяжении-сжатии
Расчеты на растяжение и сжатие статически определимых
стержневых систем
Расчет
статически неопределимых стержневых систем на растяжение-сжатие. Расчеты
по допускаемым напряжениям
Расчет гибких
нитей
Расчет статически определимых
стержней на растяжение-сжатие
Задача
1.
К двум стержням разного поперечного сечения приложены одинаковые растягивающие
силы. В каком стержне продольная сила будет больше, если А1=2А2?
Задача
2.
Как изменится продольная сила в стержне, если, не меняя растягивающей
силы, просверлить в нем отверстие?
Задача
3.
К каждому из трех вертикальных стержней одинаковой площади поперечного
сечения, но разной длины и разных материалов подвешены равные грузы. Будут ли
одинаковы напряжения в стержнях?
Задача
4.
Стальной и дюралюминиевый стержни одинаковых
размеров подвешены вертикально и соединены внизу горизонтальной балкой. В каком
стержне возникнут большие напряжения, если в середине балки приложить силу?
Сохранится ли горизонтальность балки?
Задача
5.
Натягивая провода высоковольтной линии электропередач, им дают большие
провисания. Для чего это делают?
Задача
6.
Почему струнные музыкальные инструменты нуждаются в периодической
настройке?
Задача
7.
Трещины в асфальтированных дорогах возникают чаще всего зимой.
Почему?
Задача
8.
Чтобы стакан не лопнул при наполнении его кипятком, рекомендуется
в него предварительно опустить чайную ложку и лить кипяток на ложку. Какую роль
играет в данном случае чайная ложка?
Задача
9.
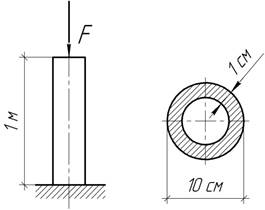
Полый цилиндрический стержень длиной l=200 мм под действием
сжимающей силы упруго укоротился на величину 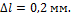 Наружный диаметр цилиндра D=40 мм, внутренний
диаметр d=30
мм. Определить величину сжимающей силы и напряжения в стержне, если модуль
упругости материала равен
Наружный диаметр цилиндра D=40 мм, внутренний
диаметр d=30
мм. Определить величину сжимающей силы и напряжения в стержне, если модуль
упругости материала равен 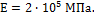
Ответ: 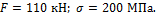
Задача
10.
Подобрать диаметр шпилек крепления цилиндра двигателя
внутреннего сгорания к картеру, считая распределения усилий между
шпильками равномерный, а допускаемое напряжение на растяжение 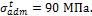 Внутренний диаметр цилиндра d=160 мм, давление газов
в цилиндре р=70 атм, число
шпилек z=14.
Внутренний диаметр цилиндра d=160 мм, давление газов
в цилиндре р=70 атм, число
шпилек z=14.
Задача
11.
Определить наибольшее сжимающие напряжения и полное ускорение
бетонной колонны постоянного сечения высотой 10 м, если один кубический метр
бетона весит 24 кН, а его модуль упругости
равен 20 Гпа.
Ответ: 0,24 Мпа; 0,06 мм.
Задача
12.
При какой длине разорвется только от собственного веса стальной стержень,
вертикально подвешенный за верхний конец? Предел прочности стали принять равным
500 Мпа.
Ответ: 6,41 км
Задача
13.
Стальной стержень круглого сечения растягивается силой 100 кН. Найти диаметр сечения, если относительное удлинение не
должно превышать 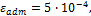 а напряжение не должно быть больше
а напряжение не должно быть больше 
Ответ: d=35,7 мм.
Задача
14.
Стальная полоса сечением 30х10 мм и длиной l=250
мм растянута силой Р=60 кН. Модуль упругости
материала полосы 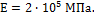 Вычислить нормальное напряжение, абсолютное и
относительное удлинение полосы.
Вычислить нормальное напряжение, абсолютное и
относительное удлинение полосы.
Ответ: 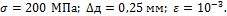
Задача
15.
К проволоке был подвешен груз. Затем проволоку согнули пополам и
подвесили тот же груз. Сравнить абсолютное и относительное удлинение проволоки
в обоих случаях.
Ответ: Абсолютное удлинение уменьшится в 4
раза, а относительное – в 2 раза.
Задача
16.
Сопоставить предельную длину свободно висящего, подвешенного за
один конец, каната, свитого из капроновых нитей, и каната, свитого из стальной
проволоки. Канат капроновой проволоки диаметром 8 мм. Вес 100 м каната 42,2 Н.
разрывное усилие 11,6 кН. Канат из стальной проволоки
диаметром 8 мм. Вес 100 м каната 221 Н. разрывное усилие 38,4 кН.
Ответ: предельная длина капронового каната 27,4
км; стального 17,4 км.
Задача
17.
Сечение растянутого стержня было подобрано из одного материала в
4 вариантах: круглое, кольцевое, квадратное, двутавровое. Стержни равнопрочны и имеют одинаковую длину. В каком варианте
масса стержня будет наименьшей и в каком –
наибольшей?
Задача
18.
К двум вертикальным стальным стержням одинаковой площади
поперечного сечения, но разной длины подвешена горизонтальная балка. Сохранится
ли горизонтальность балки, если посредине поместить груз?
Задача
19.
Два кубика, изготовленные из различных материалов и разных размеров,
сжимаются осевыми силами. При каком соотношении между силами F1 и F2 кубики получат одинаковое ускорение ребер,
параллельных силам, если Е1=2Е2
и 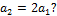
Задача
20.
Диаметр круглого стержня больше на величину Δ внутреннего
диаметра шайбы, которую требуется надеть на стержень. С какой силой F нужно растянуть
стержень, чтобы шайба свободно наделась на него?
Задача
21.
Во сколько раз увеличится наибольшее напряжение, возникающие в
призматическом стержне от собственного веса, если все размеры стержня увеличить
в 5 раз?
Задача
22.
Можно ли построить кирпичное здание в 30 этажей, обеспечив не менее
чем двадцатикратный запас прочности, если предел прочности кирпичной кладки 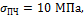 а удельный вес равен γ=16 кН/м3?
а удельный вес равен γ=16 кН/м3?
Задача
23.
Наибольшая глубина мирового океана достигает 11 км (Марианская впадина).
Каков должен быть предел упругости стальной проволоки, используемый для
измерения такой глубины?
Задача
24.
В процессе изготовления моста рабочие уложили железобетонные плиты
настила без зазора. Спрашивается, какова должна быть прочность плит на сжатие
при трехкратном запасе прочности, если температура меняется от -40 до +40 0С
и плиты были уложены зимой при температуре -10 0С? Полагая, что
напряжение в плите не должно превышать 5 МПа, вычислить минимальную величину
компенсационного зазора, если Е=20 МПа, 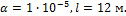
Задача
25.
В двух железобетонных колоннах различны отношения площадей
сечений арматуры и бетона Аа/Аб:
в одной это отношение равно 0,03, а во второй – 0,08. Чему равны отношения напряжений 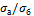 в
каждой из колонн? Зависит ли отношение напряжений от величины нагрузки? Модули
продольной упругости арматуры и бетона соответственно равны Еа=200
ГПа и Еб=20 ГПа.
в
каждой из колонн? Зависит ли отношение напряжений от величины нагрузки? Модули
продольной упругости арматуры и бетона соответственно равны Еа=200
ГПа и Еб=20 ГПа.
Задача
26.
На некоторых железных дорогах сваривают рельсы в одну непрерывную нитку. спрашивается, в каком интервале
температур должна быть произведена сварка, чтобы при колебании температуры от
-40 0С до +40 0С наибольшие сжимающие напряжения не
превосходили 75 МПа, а наибольшие растягивающие – 150 МПа. Принять Е=200 ГПа, 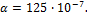
Задача
27.
К нижнему концу троса, закрепленного верхним концом, подвешен груз F = 75 кН. Трос составлен из проволок
диаметром d = 2 мм. Допускаемое напряжение для
материала троса равно [σ]
= 300 МПа. Из какого количества
проволок должен быть составлен трос?
Ответ: 80 проволок.
Задача 28.
Трещины в
асфальтированных дорогах возникают чаще всего зимой. Почему?
Задача 29.
Чтобы стакан
не лопнул при наполнении его кипятком, рекомендуется в него предварительно
опустить чайную ложку и лить кипяток на ложку. какую роль играет в данном случае чайная ложка?
Задача 30.
На некоторых
железных дорогах сваривают рельсы в одну непрерывную нитку. Спрашивается, в
каком интервале температур должна быть произведена сварка, чтобы при колебаниях
температур от минус 40оС до плюс 40оС наибольшие
сжимающие напряжения не превышали 75 МПа, а наибольшие растягивающие – 150 МПа,
если Е=200 ГПа, α=125∙10-7?
Задача 31.
Вертикально
подвешенный резиновый жгут под действием некоторого груза, прикрепленного к
нижнему свободному концу, удлиняется на 16 см. Затем он дважды складывается пополам и к
сложенному таким образом жгуту прикладывается тот же самый груз. Насколько
удлинится жгут в этом случае?
Задача 32.
Жесткость
стального провода равна 10 Н/мм. Чему равно удлинение троса, сплетенного из 10
таких проводов, если к концу троса подвесить груз весом 2 кН?
Задача 33.
При буксировке
автомобиля массы 1т результирующая сил сопротивления и
трения в 50 раз меньше веса автомобиля. Чему равна жесткость троса, если при
равномерном движении автомобиля трос удлиняется на 20 мм?
Задача 34.
Определить
ширину фундамента здания, учитывая, что среднее напряжение в грунте не должно
превышать 0,5 МПа. Общий вес фундамента, стены и полезной нагрузки на 1 м длины здания равен 500
кН/м.
Задача 35.
Какую нагрузку
сможет выдержать короткая гранитная колонна диаметром 80 см, если допускаемое
напряжение на сжатие гранита равно [σ]
= 4 МПа?
Задача 36.
Стальной
стержень кругового поперечного сечения растягивается силой 100кН. При каком
наименьшем диаметре стержня относительное удлинение не превышает 5·10-4
, а напряжение – 120 МПа?
Задача 37.
При какой
минимальной базе тензометра с коэффициентом увеличения 1000 и точностью отсчета
0,1 мм
можно обеспечить измерение напряжений в стальной детали с точностью не менее 1
МПа?
Задача 38.
Стальной
стержень кругового поперечного сечения диаметром 30 мм растянут на
испытательной машине силой 120 кН. Его продольное
удлинение, замеренное на длине 50
мм, составило 42 мкм, а изменение диаметра – 7 мкм.
Определить модуль упругости и коэффициент Пуассона материала стержня.
Задача 39.
Медная проволока диаметром 1,2
мм
удлиняется на 0,25 мм под нагрузкой 90 Н. Определить длину проволоки.
Ответ: 314 мм.
Задача 40.
Стержень из малоуглеродистой стали шириной 0,3
м и толщиной 0,015
м ослаблен
заклепочным отверстием диаметром 0,023 м, расположенным на оси стержня. Какое
растягивающее усилие этот стержень может выдержать, если допускаемое напряжение
равно 90 МПа?
Ответ: 374 кН.
Задача 41.
Прямой
стальной стержень с площадью поперечного сечения А = 5 см2 закреплен верхним концом, а к нижнему концу
приложена растягивающая сила F =30
кН. Определить относительную и продольную линейную
деформации, относительную поперечную деформацию εt, если длина стержня l = 3 м, модуль Юнга E=2∙105 Мпа, коэффициент Пуассона μ = 0,3; удельный вес
материала стержня γ=
78,5 кН/м3.
Ответ:
∆l= 0,9 мм; ε=0,0003; εt=-0,00009.
Задача 42.
Стальной
вертикальный стержень из двутавра № 30 растягивается
под действием собственного веса. Длина стержня l = 20 м. Определить нормальное напряжение в закрепленном
верхнем конце и перемещение ∆l нижнего конца стержня, E=2∙105
Мпа.
Ответ:
σ=1,54 Мпа; ∆l= 0,00785
см.
Задача 43.
Вертикальный
стержень из двух швеллеров № 20, закрепленный верхним концом, растягивается под
действием собственного веса и силы F=40 т. Определить
максимальное нормальное напряжение и перемещение ∆l нижнего конца стержня при модуле продольной упругости E=2∙105 Мпа. Длина стержня l =4 м.
Сила приложена к нижнему концу стержня.
Ответ:
σmax=84,15 Мпа; ∆l=0,171 см.
Задача 44.
Стальной болт
длиной l = 16 см при затяжке получил
удлинение ∆l= 0,12 мм. Определить напряжение в болте, если модуль Юнга E=2∙105 Мпа.
Ответ:
σ=150 Мпа.
Задача 45.
Алюминиевый стержень
круглого поперечного сечения диаметром 10 см растягивается силой F. Найти величину допускаемой силы Fadm, если допускаемое уменьшение
начального диаметра ∆d=0,002см; коэффициент
Пуассона μ= 0,35.
Ответ:
Fadm = 283 кН.
Задача 46.
Имеются две стальные
трубы, одна из которых имеет наружный диаметр D1 = 102 мм и толщину стенки t1 = 3 мм, а другая – D2 = 168 мм, t2 = 4 мм (см. рис.). Используя справочные данные в сортаменте
можно определить, что площади их поперечных сечений равны A1 = 9,3 см2; A2 = 20,6 см2. Обе трубы имеют длину l = 20 см. Вставленные осесимметрично друг в друга трубы
подвергаются сжатию силой F = 20 т.
Определить нормальные силы и напряжения, передающиеся на каждую трубу.
Ответ:
σ1=σ2= 65,62
МПа; N2 = 13779,3 кг =135,2 кН; N1 = 6220,7 кг = 61 кН.
Задача 47.
Имеются две
трубы, одна из которых стальная с наружным диаметром D1 = 102 мм и толщиной стенки t1 = 3 мм (А1 = 9,3 см2), а
другая алюминиевая с наружным диаметром D2
= 168 мм и t2 = 4 мм (А2 = 20,6 см2).
Вставленные осесимметрично друг в друга трубы подвергаются сжатию силой F = 20 т (см. рис.). Определить
нормальные силы и напряжения, передающиеся на каждую трубу. Вычислить
укорочение труб (∆l), если их длина l = 20 см, а модуль продольной упругости
для алюминия E2=6,42∙104 Мпа,
для стали – Е1
= 2,1·105 МПа.
Ответ:
N1 = 116,98 кН; σ1
= 125,76 МПа; N2 = 79,21 кН; σ2 = 38,45 МПа; ∆l= 0,12 мм.
Задача 48.
Определить
площади верхнего Ав0 и нижнего Ав1
сечений, а также вес кладки из глиняного
кирпича в форме бруса равного сопротивления сжатию, если на верхнее сечение
действует сосредоточенная сила F = 3000 кН, высота стойки l = 20 м, R = 1,5
МПа; α= 1,00.
Объемный вес кладки принять γ
= 18 кН/м3.
Ответ: Ав0 = 2
м2; Ав1 = 2,54
м2; стойка из глиняного кирпича объемом V=R∙(Ab1-Ab0)/γ=45 м3
весит Q=Vγ= 810 кН.
Задача 49.
Построить
эпюры продольной силы.
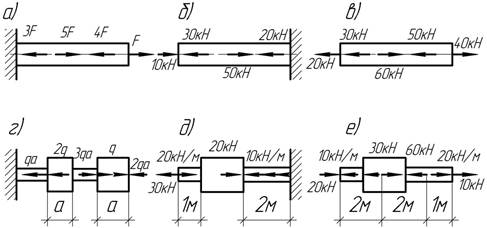
Ответ:
наибольшие по абсолютной величине силы: а) 3F (сжатие); б) 30 кН (сжатие); в) 50 кН (растяжение); г) 2qa (растяжение и сжатие);
д) 30 кН (растяжение); е) 30 кН (растяжение и сжатие).
Задача 50.
По заданной
эпюре продольной силы определить значения и направления приложенной к стержню
нагрузки.
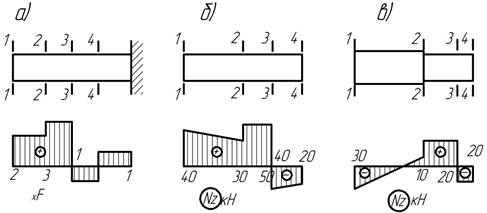
Ответ: а) F1=2F, F2=F, F4 =2F
– влево; F3=4F – вправо; б) F1=40 кН, F2=20кН, q34=20 кН/м, F4=20 кН – влево; q12=5 кН/м, F3=90 кН – вправо;
в) q12=10 кН/м,
F2=10 кН, F4=20 кН – влево; F1=30 кН, F3=40 кН – вправо.
Задача 51.
При
испытании образца сечением 20х40 показание тензометров с базой s=20 мм и коэффициентом
увеличения К=1000 составили: продольного 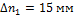 и поперечного
и поперечного 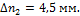 Эти показания соответствовали возрастанию
нагрузки F на 72 кН. Чему
равны значения модуля Юнга и коэффициента Пуассона материала образца?
Эти показания соответствовали возрастанию
нагрузки F на 72 кН. Чему
равны значения модуля Юнга и коэффициента Пуассона материала образца?
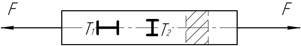
Ответ:
Е=120 ГПа, ν=0,3.
Задача 52.
Стержень, нагруженный как показано
на рисунке, удерживается в стене силами трения, равномерно распределенными по
его толщине. Построить эпюру продольных сил и определить полное удлинение
стержня.
Ответ:
Nmax=3F, 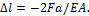
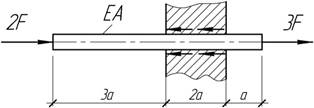
Задача 53.
Конический
и цилиндрический стержни изготовлены из одного из того же материала и находится
под действием только собственного веса. При каком соотношении длин стержней
перемещения собственного конца будут одинаковы в обоих случаях?
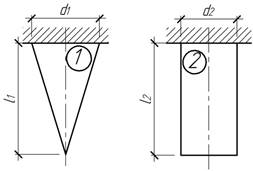
Ответ:
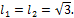
Задача 54.
Круглый
стержень диаметром d
имеет переменный вдоль радиуса модуль упругости 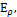 закон изменения которого показан на рисунке. Построить эпюру
напряжений, возникающих в поперечном сечении стержня
при его осевом растяжении силами F.
закон изменения которого показан на рисунке. Построить эпюру
напряжений, возникающих в поперечном сечении стержня
при его осевом растяжении силами F.

Ответ:
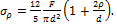
Задача 55.
Стальной
трос длиной 20 м и сечением 1 см2 туго
натянут между двумя неподвижными точками, расположенными на одной высоте.
Посредине троса прикладывается вертикальная сила F=1 кН.
Пренебрегая весом троса, определить напряжение в нем и величину δ
вертикального перемещения точки приложения силы при упругой при упругой
деформации, если Е=80 ГПа. Во сколько раз уменьшится
напряжения и величина перемещения, если уменьшить силу в 10 раз?
Ответ:
σ=100 МПа, δ=50 см; напряжения уменьшатся в 4,64 раза, а перемещение
в 2,15 раза.
Задача 56.
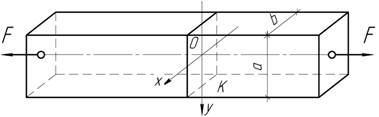
Призматический
стержень сечением ахb
растягивается осевыми силами F,
приложенными по концам. Зная координаты ХК, УК некоторой
точки К данного сечения и напряжения в этой точке,
равно 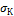 ,
требуется определить величину силы F.
,
требуется определить величину силы F.
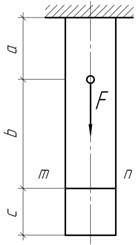
Задача 57.
Определить
перемещение сечения mn при действии на
стержень только силы F. На сколько изменится
перемещение этого же стержня, если учесть собственный вес стержня? выполнить количественную
оценку, полагая b=3a,
c=a,
F=12γAa.
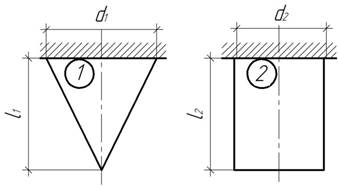
Задача 58.
Конический и
цилиндрический стержни изготовлены из одного и того же материала и находится
под действием только собственного веса. При каком соотношении длин стержней
перемещения свободного конца будут одинаковы в обоих случаях?
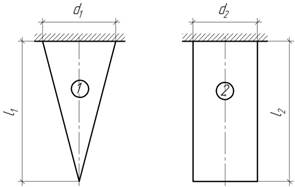
Ответ:
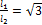
Задача 59.
Конический стержень,
защемленный верхним концом, находится под действием собственного веса.
Требуется заменить его цилиндрическим стержнем из того же материала и с таким
же перемещением свободного конца. При каком соотношении длин стержней
обеспечивается равенство перемещений?
Задача 60.
Чугунная труба
длиной 1 м нагружена сжимающей силой F=200 кН. Наружный диаметр трубы D=10 см, толщина стенки h=1 см. Вычислить величины
напряжения, относительного и абсолютного ускорений трубы, считая 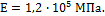
Ответ:
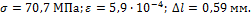
Задача 61.
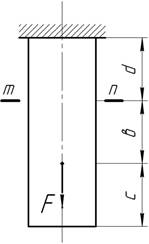
Определить с
учетом собственного веса перемещения сечения m-n
приведенного на рисунке стержня с поперечным сечением А,
модулем упругости Е и объемным весом материала γ.
Ответ:
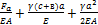
Задача 62.
Определить полное
удлинение представленного на рисунке стержня с учетом его собственного веса,
если известны объемный вес материала γ и модуль упругости Е.
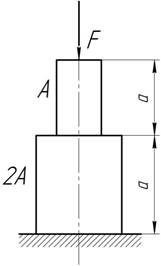
Ответ:
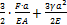
Задача 63.
При каком значении а
изменение длины однородного стержня постоянного поперечного сечения равно нулю?
Масса стержня М.
Ответ:

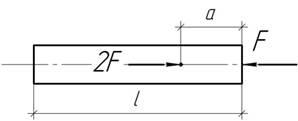
Задача 64.
Очень
длинная лента постоянного сечения А лежит на
шероховатой поверхности и под действием силы F ее конец перемещается на величину
λ. Найти закон изменения нормальных напряжений по длине ленты, если
объемный вес материала γ, модуль упругости Е, коэффициент трения f.
Ответ:
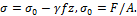
Задача 65.
Стержень
квадратного сечения, ослабленный сквозным отверстием диаметром d=2 мм, растягивается силами F=1,5 кН.
Определить сторону сечения в, если 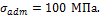
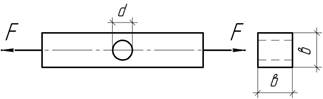
Ответ:
в=5мм
Задача 66.
Стяжка диаметром 25 мм растянута усилием F (см. рисунок),
вызывающим в ней напряжение 100 МПа.
Чему должен равняться диаметр шайбы d, чтобы давление, передаваемое ею на стену, не превышало 1,4 МПа?

Ответ: 213 мм
Задача 67.
Определить напряжения во всех участках изображенного на рисунке стального
стержня и полную его деформацию, если поперечное сечение равно 1∙10-3 м2.
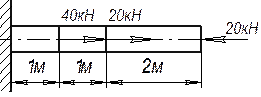
Ответ: на левом участке σ =40 МПа; на среднем σ = 20 МПа; на правом σ= -20 МПа; ∆l = 0.
Задача 68.
Стальная полоса (см. рисунок) растянута продольными силами. Она ослаблена
круглыми заклепочными отверстиями, как показано на рисунке. Определить среднюю
величину напряжений в опасном сечении.
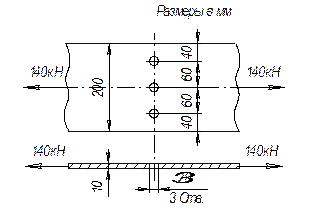
Ответ: 100 МПа.
Задача 69.
Определить напряжения в
обеих частях изображенного на рисунке стержня, а также полное его удлинение.
Материал стержня — сталь, сечение круглое.
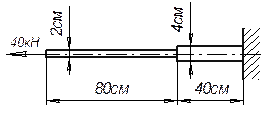
Ответ: в левой
части σ =127,6 МПа;
в правой σ =31,9 МПа; ∆l = 0,575 мм.
Задача 70.
Определить напряжение в шатуне автомобильного двигателя, поперечное
сечение I – I которого (см. рис.) имеет форму двутавра,
и проверить прочность при допускаемом напряжении [σ] = 140
МПа. Найти число шпилек n для крепления головки
цилиндра, если внутренний диаметр резьбы
dВ = 8 мм, [σ]=80 МПа. Диаметр цилиндра D = 80 мм,
давление газов р = 3,6
МПа.
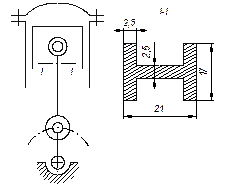
Ответ. Напряжение σШ = 144 МПа, ∆σ = 2,85%, что допустимо, число шпилек п = 5.
Задача 71.
Определить допускаемую нагрузку для стального листа толщиной t=10 мм, если допускаемое напряжение [σ] = 100 МПа (см.рис.), размеры в миллиметрах.

Ответ. Допускаемая нагрузка [F]= 140 кН.
Задача 72.
Определить
напряжение в точке О,
а также величину растягивающей силы F, зная напряжение в
точке К, равное 100 МПа.
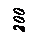

Задача 73.
При растяжении
стержня силой F = 800 кН в
точке К с координатами Хк = 4 см и Ук = 3 см возникает напряжение 160
МПа. Чему равен диаметр стержня?
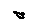

Задача 74.
Как изменится
абсолютное удлинение бруса, если:
а) увеличить
линейные размеры b и l в 2 раза;
б) увеличить
длину l в 2 раза и заменить материал (например, медь на сталь);
в) уменьшить
размер b в 2 раза, длину l в 4 раза и заменить
материал (например, сталь на титан);
г) уменьшить в
3 раза линейные размеры b, l и силу F?

Задача 75.
Для установки
тяжелой колонны в вертикальное положение требуется поднять ее левый конец. К
какой точке колонны нужно прикрепить трос, чтобы напряжения в нем были
минимальными? Выполнить проверку прочности троса при следующих данных: вес
колонны G = 200 кН,
ее длина l = 16 м, высота опоры Н = 4 м, площадь поперечного сечения троса А = 24 см2
, допускаемое напряжение [σ]
=170 МПа.

Задача 76.
Для заданных брусьев
построить эпюры продольных сил, напряжений и перемещений. Определить наибольшие
напряжения, перемещения и запасы по текучести, полагая F = qu = 10 кН, А = 2 см2, а = 20 см,
σT = 200 МПа, Е = 100 ГПа.
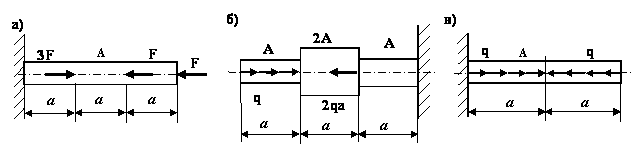
Задача 77.
Эпюры Nz для стержней, представленных на рисунке предлагается построить
самостоятельно. Для проверки тут же дается решение.

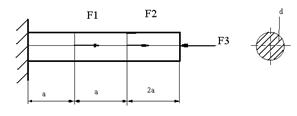
Задача 78.
Подобрать диаметр бруса, если F1=3 кН; F2=5 Кн; F3=16кН и σadm=140
МПа.
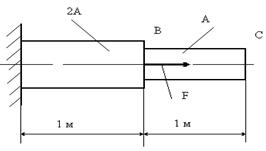
Задача 79.
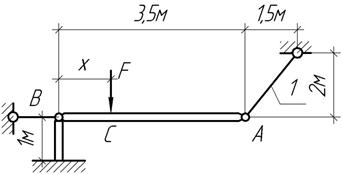
Силу перенести по линии её
действия из точки “B” в точку “C”. Что при
этом изменится ?
Задача 80.
Найти продольные силы N на участках стержня, построить
эпюру, вычислить напряжения во всех участках представленного на рисунке
стального стержня и полную его деформацию. Сила Р = 20 кН, а = 1 м,
площадь поперечного сечения стержня F=5 см2.

Ответ: На участках слева на
право σ= 80 МПа, σ= 0, σ= - 40 МПа, ∆l= 0.
Задача 81.
Построить эпюры
нормальных сил и нормальных напряжений для бруса постоянного поперечного
сечения с А = 10 см2. На брус действует
внешняя распределенная осевая нагрузка q = 5 кН/м и продольные
сосредоточенные силы F= 15 кН (рис. а).
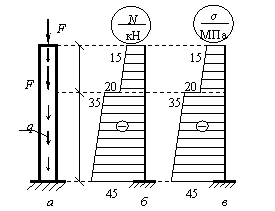
Ответ:
эпюры нормальных сил и напряжений представлены на рис. б, в.
Задача 82.
Построить
эпюры нормальных сил и нормальных напряжений для бруса постоянного поперечного
сечения с А = 10 см2. На брус действует
внешняя распределенная осевая нагрузка q = 5 кН/м и продольные
сосредоточенные силы F= 15кН (рис. а).
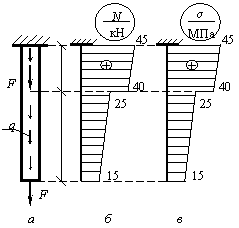
Ответ:
правильные результаты показаны на рис.
б, в.
Задача 83.
Дан прямой
стальной стержень кусочно - постоянного сечения, для
которого a = 0,4 м, а
площади поперечных сечений указаны на рис.
а.






































 Построить эпюры нормальных сил и нормальных
напряжений. Найти сечение, где действует σmax.
Построить эпюры нормальных сил и нормальных
напряжений. Найти сечение, где действует σmax.
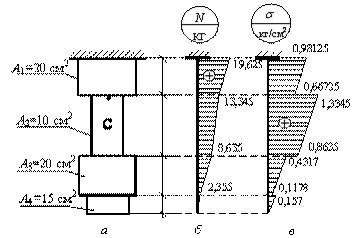
Ответ:
эпюры нормальных сил и нормальных напряжений при учете только собственного веса
стального стержня представлены на рис. б,
в , σmax= 1,3345 кг/см2 в точке С участка с площадью поперечного
сечения А2.
Задача 84.
Проверить
прочность стального стержня, изображенного на рис. а. Материал – сталь с Ry = 2450 кг/см2 и
объемным весом γ=
0,00785 кг/см3, F = 10 т, γc= 1.

Ответ:
σmax= 1429 кг/см2 < Ry = 2450 кг/см2 (см. рис. в), следовательно, условие прочности выполняется.
Задача 85.
Построить
эпюру нормальных сил для стержня замоноличенного в
массив (рис. а), предполагая, что
интенсивность сил трения постоянна по длине a. Собственным весом
стержня пренебречь.
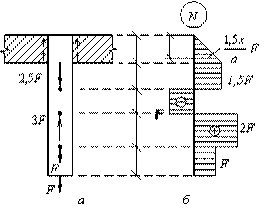
Ответ:
эпюра нормальных сил показана на рис. б.
Задача 86.
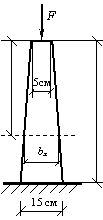
Получить аналитические
выражения для определения напряжений в поперечных сечениях бруса, имеющего
форму, показанную на рисунке. Толщину бруса принять постоянной и равной t = 2 см. Требуется: а) решить задачу, учитывая только собственный вес
бруса с γ= 78,5
кН/м3, а сжимающую силу F
принять равной нулю (F = 0); б)
решить задачу без учета собственного веса, но принять F = 200 кН; в) решить задачу, принимая F = 200 кН и, учитывая
собственный вес стального бруса с γ=
78,5 кН/м3.
Ответ:
а) 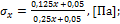 б)
б) 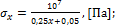 в)
в) 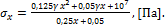
Задача 87.
Стальной
стержень квадратного сечения со сторонами ai,
находится под воздействием сосредоточенных сил
Fi, направленных вдоль оси стержня (рис. а).
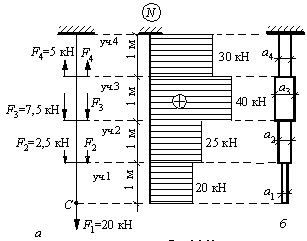
Определить
размеры поперечных сечений стержня так, чтобы в любом сечении стержня
действовали нормальные напряжения, равные расчетному сопротивлению Ry = 240 МПа.
Собственный вес стержня не учитывать.
Ответ:
a1 =0,91см; a2 =1,02
см; a3 =1,29 см; a4 =1,12 см (рис. б).
Задача 88.
Определить
допускаемую нагрузку Fadm
растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали принять Ry = 240 МПа, а γc= 1. Толщина
листа t =1 см, ширина b= 15 см.
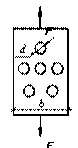
Ответ:
Fadm = 216 кН.
Задача 89.
Определить
допускаемую нагрузку Fadm
растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали принять Ry = 240 МПа, а γc= 1. Толщина листа t = 1 см, ширина b=13 см.
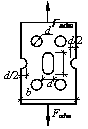
Ответ:
Fadm = 216 кН.
Задача 90.
Определить
допускаемую толщину t растягиваемого
стального листа, изображенного на рисунке, если диаметры отверстий d = 2 см, а ширина листа b = 20 см. Расчетное сопротивление стали принять: Ry = 240 МПа, а γc= 1. Внешняя
растягивающая сила F = 20 т.
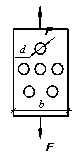
Ответ:
t≥0,58 см.
Задача 91.
В стенке
стального двутавра № 20 вырезано отверстие диаметром d = 10 см (см. рис.). Определить допускаемую на-грузку Fadm,
которая может быть приложена вдоль продольной оси ослабленного двутавра. Расчетное сопротивление стали принять Ry = 2450 кг/см2, а γc = 1,1.
Ответ:
Fadm = 571 кН.
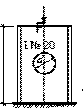
Задача 92.
В стенке
стального двутавра № 20 вырезано отверстие диаметром d = 10 см. Определить допускаемую равномерно распределенную нагрузку qadm
(кг/м), которую можно приложить вдоль стенки двутавра
(см. рис.). Расчетное сопротивление стали Ry = 2450 кг/см2, а γc= 1.
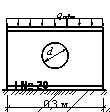
Ответ:
qadm
= 84933 кг/м = 833,19 Н/м.
Задача 93.
Определить перемещение
нижнего конца стержня, изображенного на рисунке. Дан прямой стержень
кусочно-постоянного сечения, для
которого a1 = 25 см, a2 = 15 см, a3 = 10 см, a4 = 20 см, А1
= А = 20 см2, А2 =А3 =4А, А4 = 2А. Стержень находится под действием сосредоточенных сил F1 = 327,2
Н; F2 = 1
кН; F3 = 500 Н и собственного веса с γ= 78,5 кН/м3,
действующих вдоль оси стержня. Принять E=2∙105 Мпа.
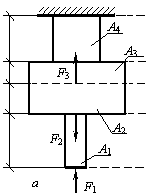
Ответ:
∆l=26/E≈0.
Задача 94.
Определить перемещение
нижнего конца стержня, представленного на рисунке. Принять
а = 0,4 м; объемный вес материала
стержня γ=7850
кг/м3.
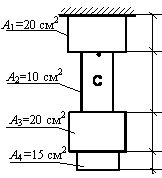
Ответ: ∆l=a∙(2,25γa+2,08∙104)/E=11146/E.
Задача 95.
Определить
линейную продольную деформацию каждого участка стержня кусочно-постоянного
квадратного сечения, изображенного на рисунке. Вычислить перемещение точки С рассматриваемого стержня и построить
эпюру перемещений поперечных сечений стержня. Принять a1 =
0,9 см; a2 = 1 см; a3 = 1,3
см; a4 = 1,1 см.
Задачу решить без учета собственного веса стержня, E=2∙105
Мпа.
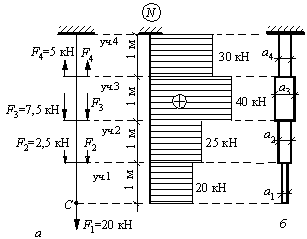
Ответ:
∆l4=1,24 мм; ∆l3=1,18 мм; ∆l2=1,25 мм; ∆l1=1,24 мм; ∆lc=4,91
мм.
Задача 96.
Стержень
постоянного поперечного сечения нагружен сосредоточенными силами (см. рис. а). Построить эпюру перемещений.
Собственный вес стержня в расчете не учитывать.
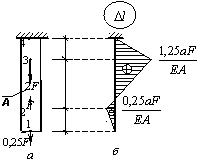
Ответ:
эпюра перемещений показана на рис. б.
Задача 97.
Определить
относительную деформацию в каждом участке стержня постоянного поперечного
сечения, показанного на рисунке. Собственным весом стержня при расчете
пренебречь.
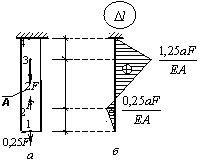
Ответ: ε12=0,25F/(EA);
ε23=-0,75F/(EA);
ε34=1,25F/(EA).
Задача 98.
Дан прямой
стержень кусочно-постоянного сечения,
для которого a1 = 25 см, a2 = 15 см, a3 = 10 см, a4 = 20 см, А1 = А =
20 см2, А2 =А3 =4А, А4 = 2А (рис. а). Стержень находится под действием сосредоточенных сил F1=327,2
Н; F2 = 1
кН; F3 = 500 Н и собственного веса с γ= 78,5 кН/м3,
действующих вдоль оси стержня.
Требуется
построить для заданного стержня эпюры нормальных сил и нормальных напряжений.
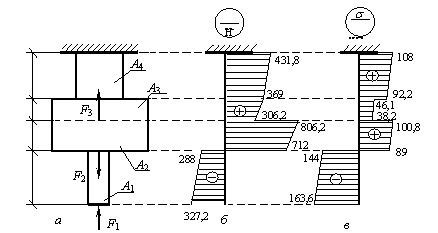
Ответ:
правильный результат показан на рис. б, в.
Задача 99.
Дан прямой
стальной стержень кусочно-постоянного сечения, для которого
а=0,4 м, а площади поперечных сечений
указаны на рис. а. При учете действия
только собственного веса стального стержня эпюры нормальных сил и напряжений
имеют вид, показанный на рис. б, в.
Как изменятся
эпюры нормальных сил и напряжений, если рассмотреть тот же стержень, но с
защемленными обоими концами. Проверить правильность вычислений, используя
критерий равенства площадей эпюры σ
с разными знаками. Найти поперечное сечение, где N = 0, σ=
0.
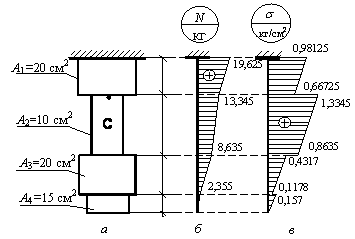
Ответ:
опорная реакция нижней опоры R =
–9,83 кг, следовательно, соответствующие
значения эпюры N, показанной
на рис. б, необходимо сложить с
величиной R = –9,83 кг.
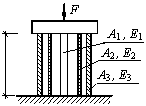
Задача 100.
Дана
конструкция, состоящая из трех элементов: двух труб разного диаметра и одного
сплошного стержня (см. рис.). Все три элемента выполнены из разных материалов с
модулями продольной упругости Е1, Е2, Е3. Площади поперечных сечений двух труб А2 и А3, а площадь поперечного сечения сплошного стержня А1. Элементы осесимметрично
вставлены один в другой и помещены между абсолютно жесткими плитами. Вся
стержневая система сжимается силой F. Требуется определить
нормальные напряжения в поперечных сечениях каждого из элементов конструкции.
Ответ:
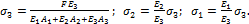
Расчет статически неопределимых
стержней при растяжении-сжатии
Задача 1.
Определить
допускаемую температуру нагрева 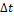 для стального стержня, если F=80 кН,
для стального стержня, если F=80 кН, 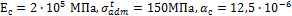
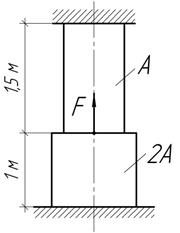
Задача 2.
Определить
допускаемую нагрузку на чугунный стержень при нагревании на 40 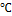 ,
если А=600 мм2,
,
если А=600 мм2, 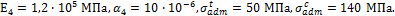
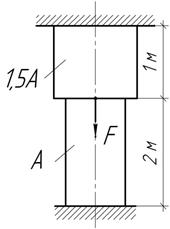
Задача 3.
Определить
напряжения в стержне при повышении температуры на 40 ,
если
,
если 

Задача 4.
Определить
допускаемую температуру охлаждения стержня, если F=100 кН, А= 500 мм2,
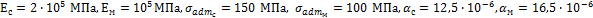
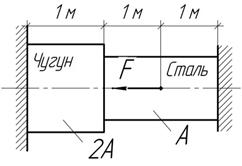
Задача 5.
Определить
напряжения по участкам стержня, если F=120кН, А=500 мм2, 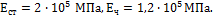 Стержень нагревается на 30
Стержень нагревается на 30 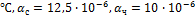
Задача 6.
Определить
допускаемую температуру нагрева стержня, если 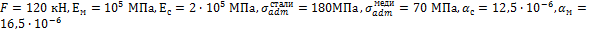
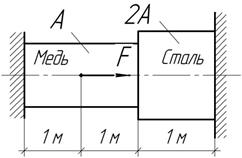
Задача 7.
Определить
допускаемую температуру стержня, если 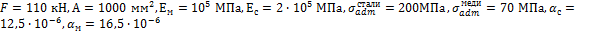
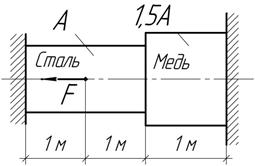
Задача 8.
Определить
допускаемую температуру стержня, если 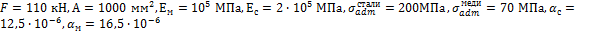

Задача 9.
Определить
допускаемую нагрузку на чугунный стержень при нагревании на 40 ,
если А=600 мм2,
,
если А=600 мм2, 
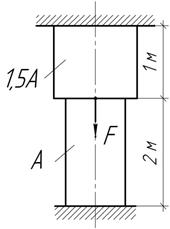
Задача 10.
Определить
допускаемую нагрузку 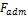 на стальной стержень при нагревании на 30
на стальной стержень при нагревании на 30 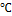 ,
если А=1000 мм2, Е
,
если А=1000 мм2, Е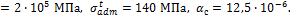
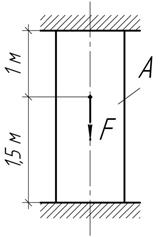
Задача 11.
Определить
напряжения в стержне при повышении температуры на 40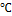 ,
если
,
если 
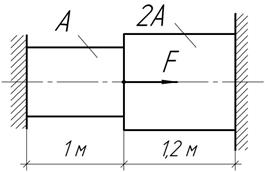
Задача 12.
Определить
допускаемую температуру нагрева 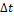 для стального стержня, если
для стального стержня, если 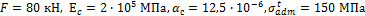
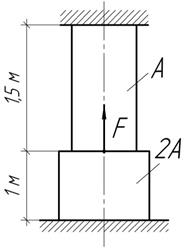
Задача 13.
Сравнить
температурные напряжения, возникающие в трех стержнях, заделанных в абсолютно
неподатливые стенки.
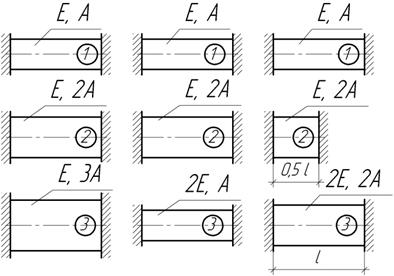
Задача 14.
В каком из трех стальных стержней возникнут наибольшие
напряжения при одинаковом изменении температуры?
Как влияет изменение сечения стержня на величину температурных напряжений?
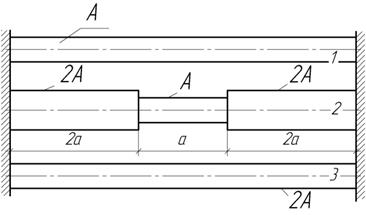
Задача 15.
Прямой
однородный стержень постоянного сечения жестко заделан по концам. В какую
сторону (вправо или влево) переместится сечение mn при равномерном
нагреве стержня?
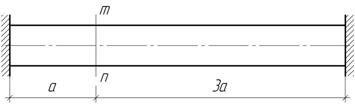
Задача 16.
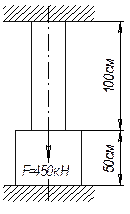
Стержень, жестко защемленный двумя концами (см. рисунок), имеет площадь
поперечного сечения верхней части 10 см2 и нижней части 40 см2. Определить напряжения
в каждой части стержня.
Ответ: σB = 50 МПа, σH= -100 МПа.
Задача 17.
Стальной болт пропущен сквозь медную трубку, как показано на рисунке. Шаг
нарезки болта равен 3 мм.
Какие напряжения возникают в болте и трубке при завинчивании гайки на 1/4
оборота?
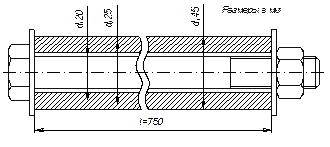
Ответ: σC =127,4 МПа; σM=- 36,4
МПа.
Задача 18.
Стержень с площадью поперечного сечения A =100 см2 защемлен верхним концом и
нагружен, как показано на рисунке. Между нижним его концом и неподатливой
плоскостью до нагружения имеется зазор ∆= 0,02 мм. Найти по способу допускаемых
нагрузок наибольшее безопасное значение силы F при [σ]
= 100 МПа.

Ответ: 2000 кН.
Задача 19.
Определить допускаемую нагрузку [F] для стального
стержня, если допускаемое напряжение [σ] =120 МПа как для растяжения, так и для сжатия.
Найти перемещение сечения I—I, если ℓ1 =
ℓ3 =2ℓ2, а ℓ2 =0,4 м, S1 = S3 = 1,5S2, S2 = 10 см2 (см. рис.).

Ответ. Нагрузка [Р]=110 кН, ∆I-I= 0,44 мм.
Задача 20.
Определить,
при каком значении размера а обеспечивается равнопрочность бруса, если предел текучести материала при растяжении
составляет две трети предела текучести при сжатии.

Задача 21.
Брус, жестко
закрепленный по концам, нагрет по всей длине на ∆T°С и нагружен силой F. Считая заданными размеры бруса, F и A, определить, при каком
значении силы F сечение mn остается
неподвижным. выполнить
количественную оценку при следующих данных: А
= 8 см2, α=12,5∙10-6, ∆T=10°С, Е=200 ГПа.

Задача 22.
Определить
нормальные напряжения в опорных сечениях стержня постоянного поперечного
сечения площадью А,
заделанного обоими концами и находящегося под действием собственного веса,
направленного вдоль оси стержня, γ
– удельный вес материала стержня. Длина
стержня – l.
Ответ:
σоп=±0,5γl.
Задача 23.
Стержень
постоянного поперечного сечения заделан одним концом. После установки стержня в
проектное положение был произведен замер величины зазора между нижним сечением
бруса и нижней опорой, который оказался равен δ=
0,5 мм, длина стержня l = 2 м,
объемный вес материала бруса γ=
78,5 кН/м3, E=2,06∙105 Мпа
(см. рис.). После этого стержень был загружен сосредоточенной силой F = 200 кН.
Определить опорные реакции RB, RC и построить
эпюры нормальных сил и напряжений.
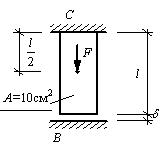
Ответ:
RB
= –48,503 кН; RC = 151,654 кН.
Задача 24.
Стержень
постоянного поперечного сечения заделан одним концом. Между нижним концом
стержня и нижней жесткой опорой имеется зазор, равный δ= 0,5 мм (см. рис.). После измерения зазора стержень был загружен своим
собственным весом с γ
= 78,5 кН/м3 и сосредоточенной силой F =200 кН. Длина стержня l=2 м, модуль продольной упругости E=2,06∙105 Мпа. Определить опорные
реакции RB, RC и построить эпюры нормальных сил и
напряжений.
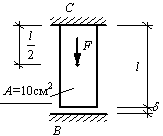
Ответ:
RB = –48,581 кН; RC = 151,576 кН.
Задача 25.
Дан стальной
прямой стержень кусочно-постоянного сечения, защемленный двумя концами и
нагруженный силой F = 10 т
(рис. а). Один из участков стержня
выполнен из двутавра № 16. Материал всей конструкции
– сталь с E=2,1∙106 кг/см2. Построить эпюры нормальных сил и напряжений.
Собственный вес элементов конструкции в расчете не учитывать.
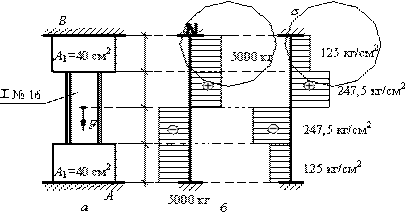
Ответ:
эпюры нормальных сил и нормальных напряжений представлены на рис.
б.
Задача 26.
Стержень
постоянного поперечного сечения А и длиной l заделан двумя концами. В
процессе эксплуатации он нагрелся на величину ∆t. Определить возникшие
внутренние усилия и напряжения.
Ответ:
N=EAα∆t;
σ=Eα∆t.
Задача 27.
Дан прямой
стальной стержень (см. рис.), находящийся под действием собственного веса с γ= 78,5 кН/м3
и сосредоточенной силы F = 1000 Н.
Эпюра внутренних нормальных усилий показана на рис. г, из которой видно, что опорная реакция RB = –857,16 Н. На сколько
градусов по Цельсию (±∆t) необходимо нагреть или
охладить весь стержень, чтобы нижняя опорная реакция RB
стала равной нулю (RB =
0)? Принять E=2,06∙105 Мпа,
коэффициент линейного расширения принять по справочной таблице.
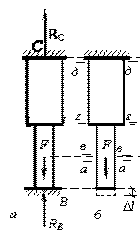
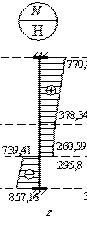
Ответ:
∆t= –0,107°.
Задача 28.
Стальной
стержень постоянного поперечного сечения заделан одним концом (см. рис.). После
установки стержня в проектное положение был произведен замер величины зазора
между нижним торцом бруса и нижней опорой, который оказался равен δ = 0,5 мм, длина
стержня l = 2 м, E=2,06∙105 Мпа, удельный вес
материала стержня γ=
78,5 кН/м3. На сколько градусов (∆t) необходимо охладить весь
стержень, чтобы опорная реакция нижней опоры была равна нулю (RB = 0) после загружения
стержня сосредоточенной силой F = 200 кН.
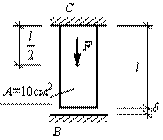
Ответ:
∆t=
–19,62°.
Задача 29.
Короткая
деревянная колонна 24х24 см, усиленная четырьмя стальными уголками 80х80х7 мм,
сжимается силой F,
передающей через абсолютно жесткую плиту. Из условия прочности конструкции
определить допустимую величину силы F,
если, 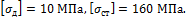
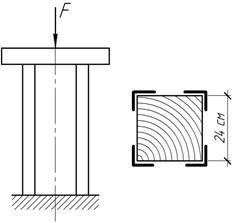
Ответ:
[F]=1150
кН.
Задача 30.
В
предварительно напряженной железобетонной колонне начальное напряжение в
стальной арматуре равно 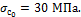 Чему равно начальное напряжение в бетоне?
Какую силу F
нужно приложить по оси колонны, чтобы напряжение в стальной арматуре стало
равным нулю? Дано: Ас=4 см2, Аσ=120 см2.
Чему равно начальное напряжение в бетоне?
Какую силу F
нужно приложить по оси колонны, чтобы напряжение в стальной арматуре стало
равным нулю? Дано: Ас=4 см2, Аσ=120 см2.
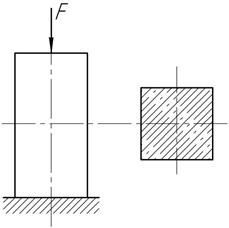
Ответ:
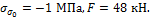
Задача 31.
Бетонная
стойка квадратного сечения 40х40 см защемлена обоими концами и в среднем
сечении нагружена силой F=320
кН. Какой площади сечения
нужно поставить две стальные тяги 1, чтобы растягивающие напряжение в верхней
части бетонной стойки не превышали 0,5 МПа? Чему в этом случае будут равны
напряжения в тягах и в нижней части стойки?
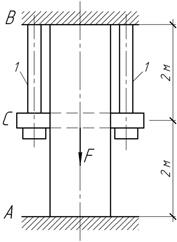
Ответ:
А1=160 см2, 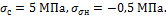
Задача 32.
Абсолютно
жесткий брус ВД должен опираться на три одинаковые деревянные стойки
квадратного сечения со стороной b.
Для уменьшения давления на фундамент средняя опора изготовлена короче крайних
на Δ=2 мм. Подобрать сечение колонн, если давление средней из них на
фундамент не должно превышать [Р]=5 МПа, допускаемое
напряжение материала [σ]=15 МПа, F=1
МН, l=4 м, Е 10 ГПа.
Ответ:
b=20
см.
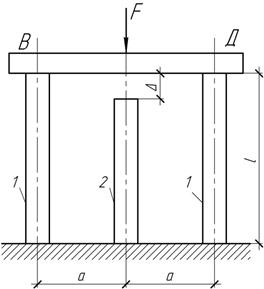
Задача 33.
Стальной
стержень постоянного сечения А= 25 см2
жестко защемлен обоими концами и нагружен сосредоточенными силами. На
расстоянии а от нижнего конца стержня
сделан сквозной пропил Δ=0,0002а.
Определить допускаемую величину силы F,
если давление стержня на фундамент в сечении Д не должно превышать [Р]=30 МПа.
Ответ:
[F]=100
кН.
Задача 34.
Чугунный круглый стержень вставлен в стальной цилиндр, причем
длина стержня больше длины трубки на Δ=0,05 мм, а площади их сечения
одинаковы, т.е. Ас=Ач=А.
Подобрать площади сечений с таким расчетом, чтобы после приложения силы F=300 кН в стержне и трубке
возникли напряжения одинаковой величины, если Ес=200
ГПа, Еч=120 ГПа, l=40 см.
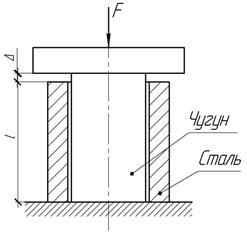
Ответ:
А=40 см2.
Задача 35.
Короткая
деревянная колонна сечением 25х25 см, усиленная четырьмя стальными уголками
40х40х4 мм, сжимается силой F,
передающийся через жесткую плиту. На сколько следует
укоротить уголки по сравнению с длиной деревянной части, чтобы обеспечить равнопрочность конструкции? Чему при этом равна допустимая
величина силы F, если 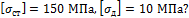
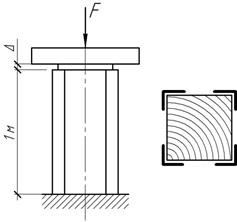
Ответ:
Δ=0,25 мм, [F]=810
кН.
Задача 36.
Стержень
квадратного поперечного сечения состоит из двух стержней, изготовленный из
разных материалов, причем Е1=3Е2.
Оба стержня имеют одинаковые размеры поперечных сечений. Полагая, что концевые пластины
абсолютно жесткие, найти значение для такого эксцентриситета е приложения силы F, при котором оба
стержня будут находиться в состоянии равномерного распределения.
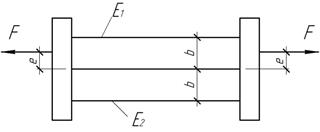
Ответ:
е=b/4.
Задача 37.
Найти,
при какой силы F
напряжения во всех сечениях стального стержня будут одинаковы, если а=1 м, А=10 см2,
Δ=0,5 мм.
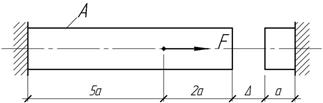
Ответ:
F=100
кН.
Задача 38.
При
каком положении сил обеспечивается равнопрочность
стержня.
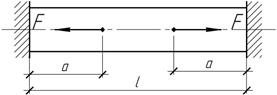
Ответ:
а=l/4.
Задача 39.
Каким
следует выбрать отношение а/b, чтобы вес
ступенчатого бруса был минимальным, если 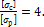
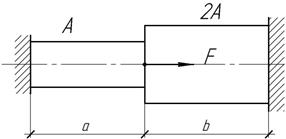
Ответ:
а/b=4.
Задача 40.
Определить
величину силы F=F1,
при которой буртик С стального стержня коснется
кольцевой опоры. При каком значении F=F2
правый торец стержня коснется опоры В? Построить эпюры
продольных сил и перемещений для следующих значений силы F: F1,
F2,
2F2.
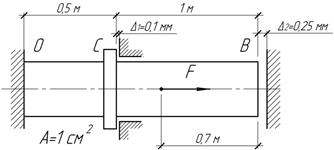
Ответ:
F1=4
кН, F2=10
кН, F=2F2:
Rв=3
кН, Rс=13
кН.
Задача 41.
Определить
допускаемое повышение температуры стального бруса и установить, на сколько
переместится при этом его среднее значение С, если [σ]=250
МПа, l=96 см.

Ответ:
Δt=500С,
Wс=
-0,1 мм (влево).
Задача 42.
Построить
эпюру продольных перемещений поперечных сечений стальных стержней при их
нагреве на 1200С, если Δ=1,2 мм, а=1 м. рассмотреть два случая: до закрытия и после закрытия зазора.
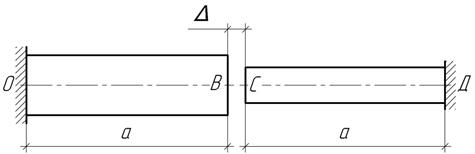
Ответ:
К моменту закрытия зазора 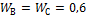 мм; после закрытия зазора Wв=0,9
мм (вправо), Wс=-0,3
мм (влево).
мм; после закрытия зазора Wв=0,9
мм (вправо), Wс=-0,3
мм (влево).
Задача 43.
Винт с
навернутой на него гайкой растягивается силами F. Выявить закон распределения
нормальных усилий по длине винта и гайки в функции z, если известно, что усилие, приходящееся
на каждый виток резьбы, пропорционально взаимному смещению винта и гайки q=K(WB-WГ);
q – усилие,
приходящееся на единицу длины нарезанной поверхности; К - экспериментально
найденный коэффициент; WB – WГ
– взаимное смещение вдоль оси винта и гайки, вызванное деформацией резьбы.
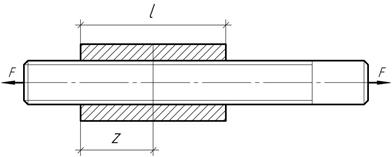
Задача 44.
На винт
навинчивается гайка, имеющая шаг резьбы, на Δ меньший шаг резьбы винта s. Каков закон распределения возникающий при этом усилии в винте и гайке и
каковы усилия на резьбу, если q=K(WB-WГ).

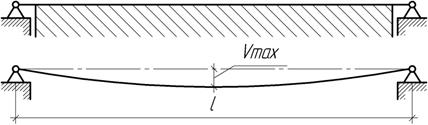
Задача 45.
Гибкая нить,
лежащая на горизонтальной плоскости, натянута силой Т0
между двумя неподвижными опорами. После того как межопорная поддерживающая
плоскость будет убрана, нить провиснет. Выясните, как зависит величина
провисания Vmax от Т0 и погонного веса
нити q, считая
заданными жесткость нити на растяжение ЕА и ее длину l.
Расчеты на растяжение и сжатие
статически определимых стержневых систем
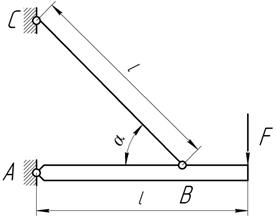
Задача 1.
Не изменяя
длины тяги ВС, найти такое ее положение (угол α), при котором масса тяги,
определенная из условия прочности, минимальна.
Ответ:
α=450
Задача 2.
Определить
безопасную (допускаемую) величину силы F, считая допускаемое напряжение материала стержней на растяжение
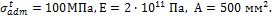
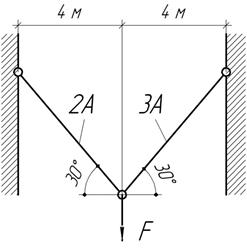
Задача 3.
Жесткая балка
ОС, деформацией которой можно пренебречь, поддерживается в горизонтальном
положении стальным стержнем ВD
длиной l=2 м. Определить диаметр стержня и при найденном размере
опускания конца балки С, если Р=60 кН, Е=200 ГПа, 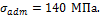
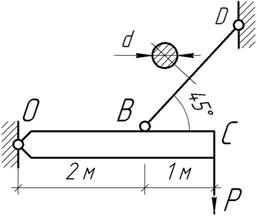
Ответ:
d=34
мм, 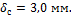
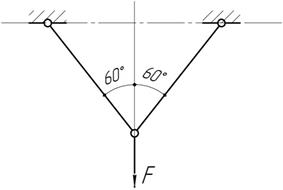
Задача 4.
Стержневая
система нагружена силой F.
Стержни изготовлены из одного материала, имеют одинаковую площадь поперечного сечения
и длину. Как изменится вертикальное перемещение точки приложения силы, если
площадь одного из стержней увеличить в два раза?
Задача 5.
Жесткий
брус ОС подкреплен деревянным подкосом ВD квадратного сечения
20х20 см и нагружен силой F.
Чему равна сила А и напряжения в подкосе, если
опускание точки С равно 
Ответ:
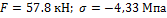
Задача 6.
Определить
напряжения в стальных стержнях, нагруженных силой F=40 кН и вертикальное перемещение узла С.
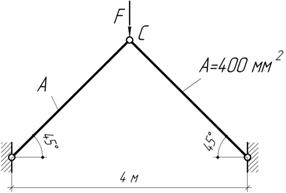
Задача 7.
Жесткий
стержень ОС нагружен силой F
и удерживается от опрокидывания круглой стальной тягой диаметром 20 мм. ИЗ
условия прочности тяги определить наибольшую допускаемую силу F а
также горизонтальное перемещение точки приложения силы, полагая 
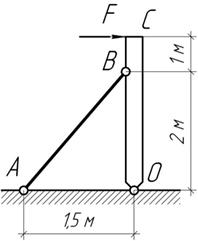
Ответ:
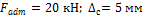
Задача 8.
Какую
наибольшую нагрузку может выдержать кронштейн, составленных из круглых
стержней, если 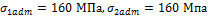
Задача 9.
Как изменится
усилие в стержне АВ, если: а) изменить его жесткость (увеличивать сечение
вдвое; уменьшить сечение вдвое; заменить материал, например, сталь на медь); б)
изменить температуру окружающей среды (повысить на +30 0С, понизить
на -20 0С); в) сделать его короче проектной длины (разумеется, в
пределах установленного допуска)?
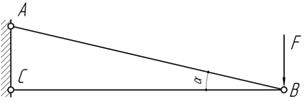
Задача 10.
Жесткий стержень АВ (см. рисунок) нагружен силой F и поддерживается стальной тягой DС круглого поперечного сечения диаметром 20 мм. Определить наибольшую допустимую
нагрузку F и опускание точки В. Допускаемое напряжение для
материала стержня СD равно 160 МПа.
Ответ: F = 12 кН, δB =
4,17 мм.
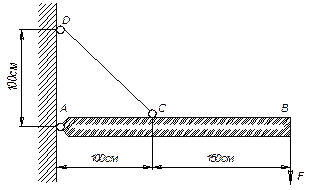
Задача 11.
Вычислить внутренние усилия и напряжения в стержнях кронштейна (см.
рис.), если нагрузка F = 35 кН. Стальная верхняя тяга круглого сечения диаметром d = 25 мм,
нижний стержень — из дерева, квадратного сечения 70 х 70 мм. Стороны кронштейна: а = 1000 мм, b =557 мм.
Ответ: N1 = 72 кН, N2 = 62,4 кН, σ1 = 146,8 МПа, σ2 = -12,7 МПа.
Задача 12.
Считая
заданными [σ], A, a определить
допустимое значение нагрузки [F].

Задача 13.
Считая
заданными [σ], a, F определить площадь поперечного сечения стержня ВС.

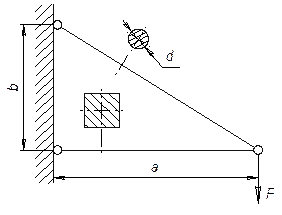
Задача 14.
Определить качественно
без вычислений перемещение узла В.
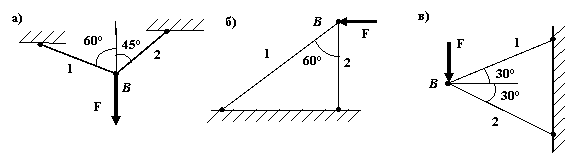
Задача 15.
В результате некоторого внешнего воздействия
длины стержней 1 и 2 изменились на ∆l1 и ∆l2 соответственно. Определить ориентировочно
полное перемещение δ
узла В.

Задача 16.
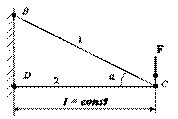
На
конструкцию, состоящую из двух стержней, действует вертикальная сила F. Оба стержня изготовлены из одного и того же материала. Длина
l горизонтального стержня СД остается постоянной, а угол α может изменяться за
счет перемещения точки
В по вертикали и соответствующего изменения длины стержня ВС.
Полагая, что допускаемые напряжения при растяжении и сжатии одинаковы и
принимая напряжения в обоих стержнях равными допускаемым, найти угол α, при котором вес
конструкции минимален.
Задача 17.
Как изменится
усилие в стержне 1, если не меняя всех прочих условий:
а) изменить
материал стержня (сталь на медь, сталь на титан, медь на титан);
б) изменить
сечение стержня (увеличить площадь сечения вдвое, уменьшить сечение вдвое) ?

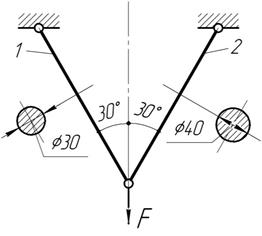
Задача 18.
К
двум стержням, угол между которыми 60 градусов, подвешен груз Р, как изображено
на рисунке. Стержень 1 круглого
поперечного сечения диаметром 30 мм с допускаемым напряжением материала 160
МПа, и стержень 2 тоже круглого
поперечного сечения, но диаметром 40 мм и с допускаемым напряжением материала
60 МПа. Какой наибольший груз Р может выдержать эта конструкция?
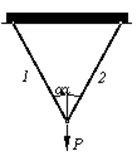
Ответ: Наибольший допускаемый
груз, которую выдерживает конструкция Р=130 кН.
Задача 19.
Определить
усилия в стержнях BС и СD (см. рис.), подобрать сечение
растянутого стержня ВС при условии, что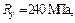 а коэффициент условий
работы γс = 1.
а коэффициент условий
работы γс = 1.
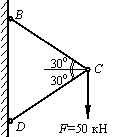
Ответ: NBC = 50 кН; NCD = –50 кН; АВС = 2,08 см2.
Задача 20.
Определить
площади поперечных сечений стальных элементов АВ и СВ
кронштейна, показанного на рисунке, если F =
5 т, γс=1, Ry=2450 кг/см2.

Ответ:
ААВ = 2,89 см2; АСВ
= 3,94 см2 (без учета
потери устойчивости).
Задача 21.
Два абсолютно
жестких бруса СD и СВ соединены
шарниром в точке С
и опираются на опоры в точках D и В (см. рис.). Нижние концы брусьев соединены стальной затяжкой
длиной l = 2 м. Подобрать сечение стальной
затяжки (АВD), если F = 200 кН, Ry = 240 МПа, γс = 1. Определить удлинение затяжки ВD, если
Е = 2,06·105 МПа.

Ответ:
АВD
= 2,4 см2;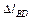 = 0,23 см.
= 0,23 см.
Задача 22.
Определить
допускаемое значение силы F, действующей
на стальной кронштейн (см. рис.), если принято расчетное сопротивление стали γс=1, Ry=2450 кг/см2.
Площади поперечных сечений стержней АВ
и СВ
известны и равны ААВ = 1 см2, АСВ = 2 см2.

Ответ:
Fadm = 1,73 т = 16,97 кН; второй результат Fadm,2 = 2,53 т = 24,82 кН во внимание не принимаем.
Задача 23.
Определить
допускаемое значение силы F,
действующей на конструкцию, изображенную на рисунке, если расчетное
сопротивление материала тяги АВ 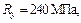 а γс=1.
Площадь поперечного сечения тяги АВ ААВ=1
см2. Стержень ВС – абсолютно жесткий.
а γс=1.
Площадь поперечного сечения тяги АВ ААВ=1
см2. Стержень ВС – абсолютно жесткий.

Ответ:
Fadm = 13,86 кН.
Задача 24.
Два абсолютно
жестких бруса В
и С (см. рис.) соединены между собой
тремя стержнями, из которых крайние стержни – стальные с модулем Юнга Еc =
2,06·105 МПа, средний стержень – медный с модулем Юнга ЕM = 1,3·105 МПа.
Площади поперечных сечений всех стержней одинаковы и равны А = 1см2, расстояния
между абсолютно жесткими брусьями l =1
м.
Определить
нормальные усилия в стержнях, если
расстояния между брусьями увеличить на ∆l= 0,0001 м. Найти значение силы F, которая
обеспечит увеличение расстояния между брусьями В и С на заданную величину ∆l.

Ответ:
Nc = 2,06
кН – в стальных стержнях; Nм = 1,3 кН – в медном стержне; F = 5,42 кН.
Задача 25.
К двум
абсолютно жестким брусьям В
и С приложены сосредоточенные силы F = 54,2 кН (см.
рис.). Брусья В
и С соединены между собой тремя
стержнями, из которых крайние – стальные с Еc = 2,06·105 МПа, а
средний – медный с ЕM = 1,3·105 МПа.
Площади поперечных сечений принять одинаковыми и равными А = 1 см2, а l = 1 м. Вычислить удлинения стержней ∆lc и
∆lм, а также значения нормальных усилий,
возникающих в стержнях.

Ответ:
Nм = 13 кН, Nc =
20,6 кН; ∆lc=∆lм=
0,001 м.
Задача 26.
Два абсолютно
жестких бруса В
и С соединены между собой тремя
стержнями, из которых крайние – стальные с модулем упругости Е1=2,06·105 МПа, и
температурным коэффициентом линейного расширения α1=120∙10-7, а
средний стержень – медный с модулем упругости Е2 = 1,3·105 МПа и с α2=170∙10-7 (см. рис.). Площади
поперечных сечений всех стержней одинаковы. Определить нормальные напряжения в
поперечных сечениях стержней, возникающие при повышении температуры всех трех
стержней на 45о. Принять F = 0.

Ответ:
σ1=
11,12 МПа; σ2=
–22,24 МПа.
Задача 27.
В
результате некоторого внешнего воздействия длины стержней АВ и АС изменились на
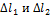 соответственно.
Определить полное перемещение δ узла А и угол
γ между направлением этого перемещения и вертикалью.
соответственно.
Определить полное перемещение δ узла А и угол
γ между направлением этого перемещения и вертикалью.
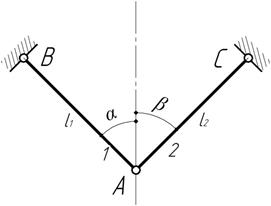
Ответ: 
Задача 28.
Считая брус СD недеформируемым, проверить
прочность и жесткость стержневой системы, если F=10 кН, А1=А2=2
см2, а=2 м, Е=200 ГПа,
[σ]=120 МПа, [δс]=10 мм.
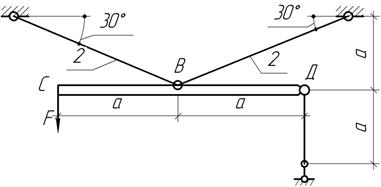
Ответ:
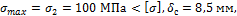 т.е. прочность и жесткость обеспечены.
т.е. прочность и жесткость обеспечены.
Задача 29.
Считая брусья АВ и СD недеформированными, определить из
расчетов на прочность и жесткость требуемые площади поперечных сечений
стержней, если А1=А, А2=А3=5А,
q=100
кН/м, а=1 м, [σ]=140 МПа, Е=200
ГПа, [δс]=2,5 мм.
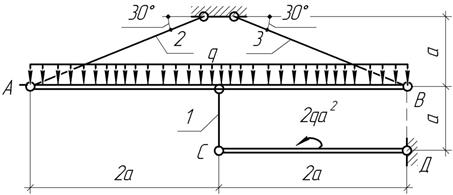
Ответ: А=10 см2 (из условия жесткости).
Задача 30.
Считая брус
АС недеформируемым, определить из расчетов на прочность и жесткость величину
допускаемой нагрузки F,
если А1=10 см2, А2=А3=4А1,
а=1 м, [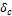 ]=2,5
мм; [σ]=120 МПа.
]=2,5
мм; [σ]=120 МПа.
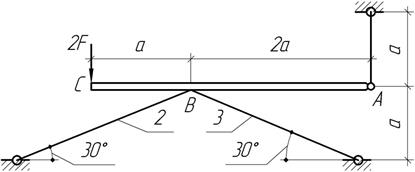
Ответ:
[F]=100 кН (из условия
жесткости).
Задача 31.
Считая брус
АВ недеформируемым, определить напряжения в элементах конструкции, а так же
опускание точки С, если А1=10 см2,
А2=100 см2, А3=30 см2, Е1=200
ГПа, Е2=10 ГПа, Е3=100 ГПа, F=200 кН, а=1 м.
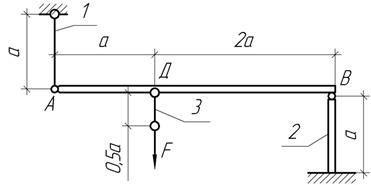
Ответ:
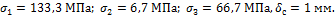
Задача 32.
Жесткий
брус АВ подвешен на двух круглых тягах: тяга 1 диаметром 25 мм – медная, а тяга
2 диаметром 20 мм – стальная. На каком расстояние а необходимо приложить силу F=30 кН, чтобы в
процессе деформации груз оставался горизонтальным? Какие в этом случае возникают
напряжения?
Ответ:
а=0,92 м, 
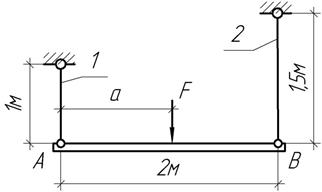
Задача 33.
Жесткий
брус АВ поддерживается круглой стальной тягой диаметром 20 мм и опирается на
деревянную стойку 2 квадратного сечения 20х20 см. На каком расстоянии х нужно
поместить силу F,
чтобы опускание точки А было вдвое меньше опускания
точки В?

Ответ:
х=6,9 см.
Задача 34.
Жесткий
брус АВ поддерживается круглой стальной тягой диаметром 20 мм и опирается на
деревянную стойку 2 квадратного сечения 20х20 см. Определить значение силы F, при котором опускание
точки С равно 1 мм. Чему при этом равны напряжения в
тяге 1 и в стойке 2?
Ответ:
F=412
кН, 
Задача 35.
Жесткий
брус ОС нагружен силой F
и удерживается от опрокидывания круглой стальной тягой диаметром 20 мм. Из
условия прочности тяги определить наибольшую допускаемую силу F, а также
горизонтальное перемещение точки приложения силы, полагая [σ]=160 МПа.
Ответ:
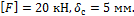
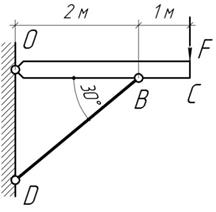
Задача 36.
Жесткий
брус ОС подкреплен деревянным подкосом ВД квадратного сечения
20х20 см т нагружен силой F.
Чему равна сила напряжения в подкосе, если опускание точки С
равно 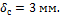

Ответ:
F=57,8 кН, σ= -4,33 МПа.
Задача 37.
Кронштейн
выполнен из круглого стального стержня АС диаметром d и деревянного подкоса ВС квадратного
сечения со стороной b.
Подобрать размеры поперечных сечений элементов системы, если допускаемое
напряжение для стали равно 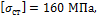 а для дерева
а для дерева 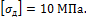 При найденных размерах определить
горизонтальное, вертикальное и полное
перемещение узла С.
При найденных размерах определить
горизонтальное, вертикальное и полное
перемещение узла С.
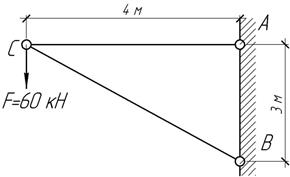
Ответ:
d=25
мм, b=100
мм, 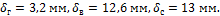
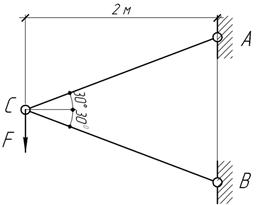
Задача 38.
Кронштейн
выполнен из двух стальных стержней. Стержень АС состоит из двух швеллеров №12,
а ВС из двутавра № 24. Определить наибольшую
допускаемую силу F
и вертикальное перемещение узла С, если 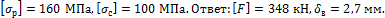
Задача 39.
По
абсолютно жесткой балке АВ, подвешенной на двух стержнях, перемещается груз F. При каком положении
груза балка будет горизонтальна? Насколько длина первого стержня должна
отличаться от проектной длины, чтобы балка была горизонтальна при заданном положении
груза z=2a.
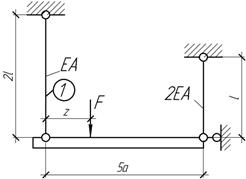
Ответ: z=4a, 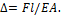
Задача 40.
При
каком значении угла φ направление перемещения узла В
будет совпадать с направлением силы F,
если 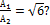
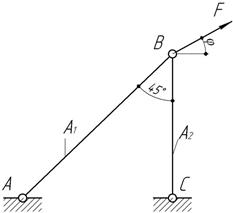
Ответ:
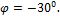
Задача 41.
При
каком соотношении между углами α и β в стержнях не возникают
температурные напряжения, если материал стержней и температура их нагрева
одинаковы. Расстояние узла В от опорной поверхности АС
постоянно (h=const).
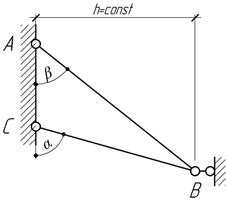
Ответ:
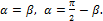
Задача 42.
При
сборке двухстержневого узла ВСД оказалось, что
стержень ВС имеет длину, превышающую номинальный размер на 3,2 мм. Поэтому узел В получил начальное горизонтальное смещение вправо. После
нагрузки узла силой F
он оказался смещенным на 2 мм влево от вертикали ВД. Определить силу F, если площадь сечения
стержней А=3 см2, модуль упругости Е=200
ГПа.
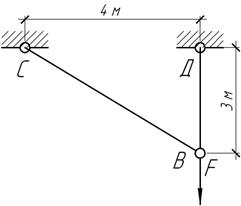
Ответ:
F=160
кН.
Задача 43.
Сила
F
совершает медленное вращательное движение в плоскости стержневой конструкции.
Определить из условия прочности угол α, при котором конструкция будет
иметь наименьший вес. Площади сечения стержне одинаковы.
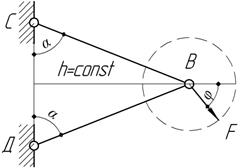
Ответ:
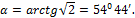
Расчет
статически неопределимых стержневых систем на растяжение-сжатие. Расчеты
по допускаемым напряжениям
Задача 1.
Как
изменится усилие в стержне 1 статически неопределимой системы, если, не меняя
всех прочих условий: а) изменить материал стержня (сталь на медь, медь на
титан); б) изменить сечение стержня (увеличить сечение вдвое, уменьшить сечение
вдвое)?
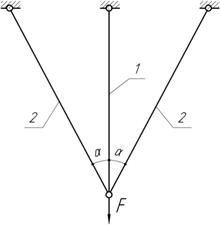
Задача 2.
При
определении сборочных усилий в статически неопределимой системе было принято,
что стержень 1 короче проектной длины на величину 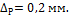 При этом наибольшее усилие в системе оказалось
равным 10 кН. На практике фактическая неточность оказалось равной
При этом наибольшее усилие в системе оказалось
равным 10 кН. На практике фактическая неточность оказалось равной 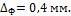 Спрашивается, на сколько фактическое
максимальное усилие будет отличаться от расчетного?
Спрашивается, на сколько фактическое
максимальное усилие будет отличаться от расчетного?
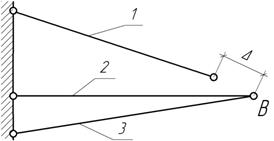
Задача 3.
При
определении температурных усилий в статически неопределенной системе было
принято, что монтаж системы производится при температуре 0 0С, а
температура окружающей среды колеблется от -40 0С до +400С.
Наибольшее усилие в стержне 2 по расчету оказалось равным 5 кН.
На практике монтаж системы произвели при температуре +20 0С.
Насколько фактическая наибольшее усилие в стержне 2 будет отличаться от расчетного?
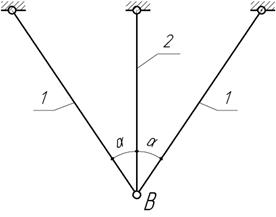
Задача 4.
Жесткая балка поддерживается двумя подвесками, как показано на рисунке.
Первая подвеска должна иметь площадь поперечного сечения, в два раза большую,
чем вторая; материал подвесок - сталь с
допускаемым напряжением [σ]
= 160 МПа. Подобрать безопасные
размеры сечения подвесок.
Ответ: F1 = 7,5 см2, F2 =
3,75 см2.
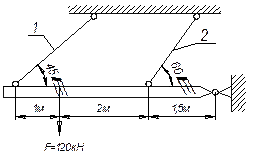
Задача 5.
Жесткий брус (см. рис.), кроме шарнирной опоры, поддерживается еще двумя стальными
тягами одинакового поперечного сечения площадью 40 см2. После установки тяг их
температура повысилась на ∆t = +20°. Определить напряжения в
тягах.
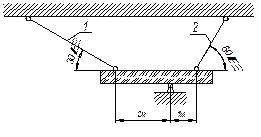
Ответ: 𝜎1= - 47 МПа; σ2= - 54,2 МПа.
Задача 6.
Жесткая балка (см. рисунок) подвешена на двух
стержнях. Площадь сечения первого стержня 10 см2,
второго стержня 15 см2, пределы
текучести материалов стержней соответственно равны σT1=260 МПа, и σT2=150 МПа. Определить
по способу допускаемых нагрузок величину безопасной нагрузки F, если коэффициент
запаса равен 2.
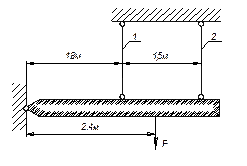
Ответ: 252 кН.
Задача 7.
Составить
уравнения совместимости деформаций для заданных стержневых систем
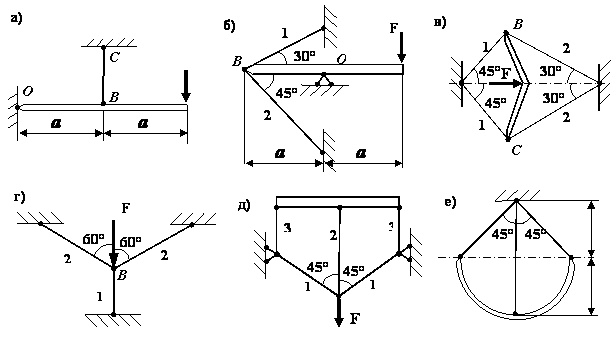
Задача 8.
При
определении температурных усилий в стержневой системе было принято, что монтаж
производится при температуре плюс 10ºС, а температура
окружающей среды колеблется от минус 40ºС до плюс 40ºС. Наибольшее
усилие в стержне 2 по расчету сказались равными 50 кН.
На практике монтаж системы произвели при температуре плюс 20ºС. На сколько
фактическое наибольшее усилие в стержне 2 будет отличаться от расчетного?

Задача 9.
При
определении сборочных усилий в стержневой системе было принято, что стержень 1
короче проектной длины на величину ∆p= 0,3 мм. При этом наибольшее
усилие в системе оказалось равным 20 кН. На практике
фактическая неточность оказалась равной ∆ф=
0,45 мм.
Спрашивается, на сколько фактическое максимальное усилие будет отличаться от расчетного?

Задача 10.
Какие
напряжения возникнут в стержнях при нагревании их на одну и ту же температуру ∆Е=80
°С, если α =12,5∙10-6, Е=200
ГПа?
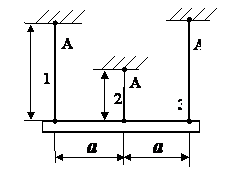
Задача 11.
Жесткий брус ВД должен быть подвешен на трех
одинаковых стержнях и воспринимать нагрузку F. Однако один из
стержней изготовили короче проектной длины на величину ∆. Где этот короткий стержень
целесообразно установить: в центре или на краю? Обоснуйте ваше заключение,
считая заданными ∆,
А, Е и F.

Задача 12.
Перемещение
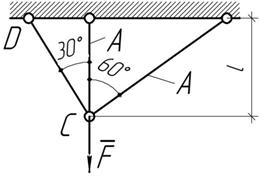
узла С в направлении силы F составило 0,08 см. Принимая l=1м, А=1см2, 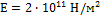 и считая брус CD абсолютно жестким, найти величину силы F.
и считая брус CD абсолютно жестким, найти величину силы F.
Задача 13.
Три стальных
стержня с одинаковыми площадями поперечных сечений А прикреплены шарнирно к
абсолютно жесткой балке ВС (см.
рис.), на которую действует сосредоточенная сила F=50 кН. Определить необходимую площадь
поперечных сечений А трех стержней,
если расчетное сопротивление стали стержней Ry =240 МПа, а коэффициент условий работы γс = 1.

Ответ:
NB=NC=0,4F; ND=0,2F; А = 0,83 см2.
Задача 14.
На рисунке
изображена стержневая система, состоящая из недеформируемого бруса АВ, шарнирно опертого в точке В и подвешенного
на трех стержнях. Для решения задачи принять q = 10 кН/м, a=2 м, А1=5
см2, А2=20 см2,
А3 =10 см2, β=
60°.
Определить
нормальные силы, возникающие в стержнях.
У к а з а н и е. На рис. б
показана расчетная схема рассматриваемой стержневой системы. Пунктирная линия ВЕ/
показывает положение жесткого стержня ВЕ
после приложения внешней нагрузки. В качестве уравнения равновесия принять ΣMB=0.

Ответ:
N1 = 1,04qa = 20,8 кН; N2 = –180 кН; N3 = 156 кН.
Задача 15.
Определить
нормальные напряжения в трех стальных стержнях, на которых подвешена абсолютно
жесткая балка СD (см. рис.) с грузом F = 5000
кг.

Ответ:
σ1=
500 кг/см2 = 49,1 МПа; σ2=
750 кг/см2 = 73,6
МПа; σ3=
98,1 МПа.
Задача 16.
Абсолютно
жесткая балка ОС опирается на
шарнирно неподвижную опору О и поддерживается двумя гибкими связями ВD и СЕ (см. рис.). Определить внутренние усилия в связях ВD и СЕ, если a=3 м, b=2,6 м; с=1,6 м.
Связи изготовлены из одного материала.

Ответ:
NBD = 0,1388Q; NCE =
0,299Q.
Задача 17.
Проверить
прочность стержневой системы, выполненной из трех одинаковых стальных стержней
сечением А=10 см2, если F=240 кН, 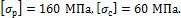
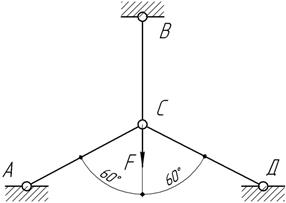
Ответ:
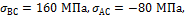 т.е.
прочность недостаточна.
т.е.
прочность недостаточна.
Задача 18.
Подобрать
необходимое сечение стальных тросов, поддерживающих стальную мачту, на которую
действует ветровая нагрузка постоянной интенсивности q=600 Н/м. Тросы имеют одинаковое сечение
и работают только на растяжение. Деформацией мачты и начальным натяжением
тросов пренебречь. Дано: а=19 м, [σ]=160 МПа.

Ответ:
А= 1 см2.
Задача 19.
Прямой
брус АС защемлен обоими концами и подкреплен двумя симметрично расположенными
подкосами. Подобрать сечения бруса и подкосов из условия прочности конструкции,
если F=330
кН, 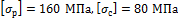 ,
Е1=Е2, А1/А2=4.
,
Е1=Е2, А1/А2=4.
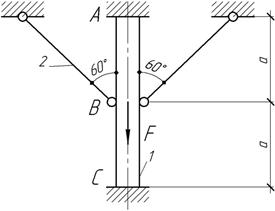
Ответ:
А1=20 см2.
Задача 20.
Три
одинаковых стержня шарнирно скреплены в узле В, к
которому приложена сила F=120
кН. Определить площадь сечения стержней, полагая, [σ]=160 МПа.
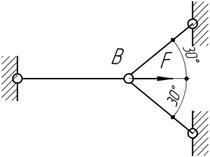
Ответ:
А=3 см2.
Задача 21.
Жесткая
балка первоначально опиралась правым концом на чугунную стойку сечением 100 см2
и не имела промежуточных опор. затем
были поставлены две промежуточные деревянные стойки круглого сечения диаметром
25 см. На сколько процентов можно увеличить нагрузку после установки
промежуточных опор при условии, что напряжения в чугунной стойке останутся
первоначальными?
Ответ:
На 41%.
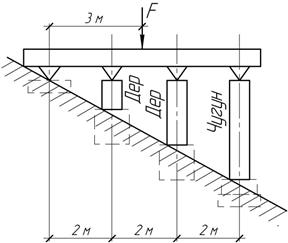
Задача 22.
Стальной
стержень ВД нижним концом опирается на жесткий фундамент, а верхним подкреплен
к балке, податливость которой в точке В определяется
коэффициентом α=3 мкм/кН. Чему равны напряжения
в стержне, если F=675
кН, А=25 см2, а=1 м?
Ответ:
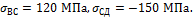
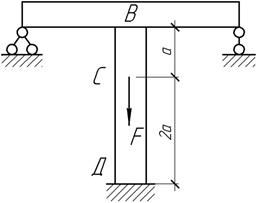
Задача 23.
Жесткий
брус ВД подвешен на трех стальных стержнях одинаковой площади поперечного
сечения А. Определить перемещение точки В.
Ответ:
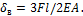
Задача 24.
Определить
напряжения в стержнях системы после нагрева среднего стержня на 65 0С.
Горизонтальный стержень дюралюминиевый сечением Ад=3 см2
и модулем упругости Ед=70
ГПа. Наклонные стержни из стеклопластика СВАМ с Ас=8 см2 и Ес=35
ГПа. Температурный коэффициент линейного расширения дюралюминия равен 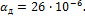
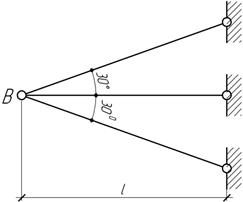
Ответ:
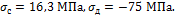
Задача 25.
На
какую величину Δ надо укоротить правую тягу с помощью стяжной гайки К, чтобы жесткий брус весом G, подвешенный на трех одинаковых тягах,
оставался горизонтальным?

Ответ:
Δ=0,1Gl/(EA).
Задача 26.
Стержни
1 и 2 отличаются только длиной. На каком расстоянии х следует поставить опору О, чтобы обеспечить равнопрочность
стержней? Деформациями детали ОВС пренебречь.
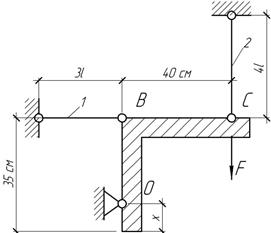
Ответ:
х=5 см.
Задача 27.
Сила
F
приложена в центре колеса, имеющего 12 стальных спиц одинаковой длины и
одинакового поперечного сечения А, которые делят
окружность на равные секторы. Считая обод колеса абсолютно жестким, определить
опускание точки приложения сил. Спицы при сжатии не теряют устойчивость и
деформации их такие же, как в растянутых спицах при одинаковом усилии.
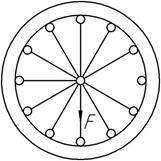
Ответ:
δ=Fl/(6EA).
Задача 28.
Абсолютно
жесткий брус переместился под действием силы F=640 кН, как показано на рисунке
штриховой линией. Вычислить напряжения в стержнях, возникающие при нагружении, и напряжения, которые останутся в стержнях
после снятия нагрузки, если l=1 м, А=10 см2, Е=200 ГПа, 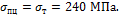
Ответ:
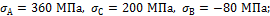 после снятия нагрузки
после снятия нагрузки 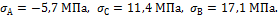
Задача 29.
Под
действием силы F
узел К переместился по вертикали на величину 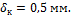 Найти величину и направление силы F, если l=1
м, А=1 см2, Е=200 ГПа.
Найти величину и направление силы F, если l=1
м, А=1 см2, Е=200 ГПа.
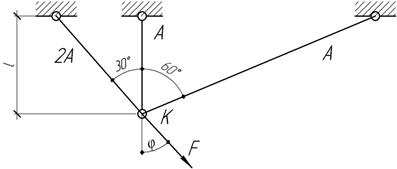
Ответ:
F=24,8 кН, 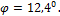
Задача 30.
Определить
усилия в стержнях плоской фермы, загруженной в узлах радиальными силами F. Жесткость ЕА всех
стержней одинакова.
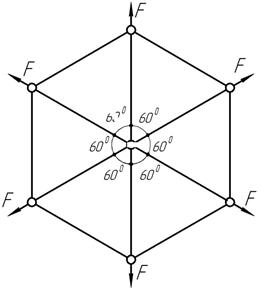
Ответ:
N=F/2.
Задача 31.
Абсолютно
жесткий брус АВ подвешен на трех параллельных стальных стержнях. Температура
среднего стержня повышается, а температура крайних стержней понижается на одну
и ту же величину 400С. Определить напряжения в стержнях и величины
перемещений точек С и Д, считая, что стержни не теряют
устойчивость равновесия.
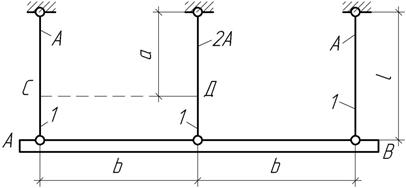
Ответ:
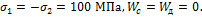
Задача 32.
К
крайнему узлу О полубесконечной
стержневой системы приложена сила F.
Определить перемещение этого узла, если жесткость всех стержней одинаковы и равны ЕА.
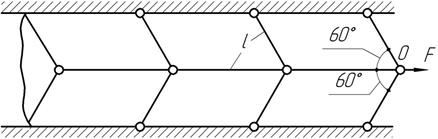
Ответ:
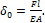
Задача 33.
Определить
тормозящий момент и перемещение конца рычага (точка К) ленточного тормоза в
зависимости от силы F.
Коэффициент трения на поверхности соприкасания ремня
со шкивом f,
а жесткость ремня на растяжение ЕА. Рычаг и шкив рассматривать как абсолютно жесткие.
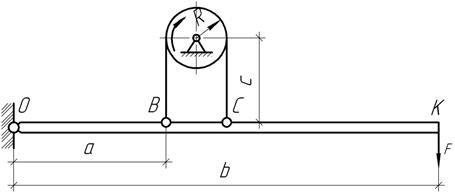
Задача 34.
Определить
тормозящий момент и перемещение конца рычага (точка К) ленточного тормоза в
зависимости от силы F.
Коэффициент трения на поверхности соприкасания ремня
со шкивом f, а
жесткость ремня на растяжение ЕА. Рычаг и шкив рассматривать как абсолютно жесткие. Решить задачу, учитывая, что шкив вращается в
противоположном направлении.
Расчет
гибких нитей
Задача 1.
Медный провод
с площадью сечения 34,1 мм2 и начальной
длиной 50 м подвешен к опорам, расположенным на одном уровне и отстоящим друг от
друга на расстоянии 50 м. определить, на сколько процентов увеличится натяжение
провода, вызванное его обледенением, если диаметр провода d0=8 мм, а обледеневшего d=20 мм; плотность льда 900
кг/м3; Е=85 ГПа; ρ=8900 кг/м3.
Ответ:
на 48%
Задача 2.
Стальной канат
с площадью поперечного сечения 46 мм2
закреплен к опорам, расположенным на одном уровне и удаленным друг от друга на
расстоянии 50 м со стрелой провисания 2 м. Определить напряжения в канате, если
вес 1 м каната равен 3,8 Н.
Ответ:
σ=51,6 МПа
Задача 3.
Между опорами,
удаленными друг от друга (по горизонтали) на расстояние l=60 м и
расположенными одна выше другой на расстоянии 5 м, подвешен медный провод с
площадью сечения 68,3 мм2 и начальной (в
ненапряженном состоянии) длиной 60,1 м. Определить натяжение провода при
гололёде; вес 1 м провода равен 6,2 Н, а с учетом обледенения – 22,3 Н,
Е=85ГПа, ρ=8900 кг/м3.
Ответ:
13 кН
Задача 4.
Висящий мост
поддерживается двумя стальными цепями. Пролет цепей равен 120 м, а их стрела провисания
10м. Собственный вес конструкции моста вместе с временной (полезной) нагрузкой
составляет 60 кН/м. Определить необходимую площадь поперечного сечения каждой
цепи при [σ]=400 МПа.
Ответ:
142,5 см2
Задача 5.
Медный провод
подвешен между двумя точками А и В, расстояние между
которыми l=50 м. Определить допустимое
натяжение провода Т, величину натяжения в нижней точке Н и стрелу провисания f. Дано: диаметр сечения
провода d=4 мм,
плотность материала ρ=8000 кг/м3, допускаемое напряжение
[σ]=50 МПа.
Ответ:
f=0,5 м, Н=Т=615Н.
Задача 6.
Горизонтальное
расстояние между опорами провода сечением 1 см2
равно 37 м. Одна опора ниже другой на 30 см, и наинизшая
точка провода расположена на 90 см ниже нижней опоры. Определить горизонтальное
расстояние от нижней опоры до наинизшей точки провода
и натяжение в этой точке, если удельный вес провода равен 8000 кг/м3.
Ответ:
17,1 м; Н=1,31 кН.
Задача 7.
Какой
начальной длины (в ненапряженном состоянии) должен быть взят медный провод,
чтобы при его подвеске к опорам, расположенном на одном уровне на расстоянии 50
м, стрела провисания была равна 3 м, Е=85ГПа, ρ=8900 кг/м3.
Ответ:
l0=50,475 м
Задача 8.
Алюминиевый
провод с площадью сечения 396 мм2 линии электропередач
подвешен между опорами, расположенными на одном уровне и удаленными друг от
друга на 200 м. провод подвешен со стрелой l0=8 м при
температуре t0=30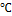 .
На сколько градусов может быть понижена температура, чтобы натяжение провода не
превышало 8 кН, Е=50 ГПа.
.
На сколько градусов может быть понижена температура, чтобы натяжение провода не
превышало 8 кН, Е=50 ГПа.
Ответ:
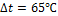
Задача 9.
Определить
напряжение в стальной и алюминиевых частях
проволочного сталеалюминевого кабеля, подвешенного к двум опорам
расположенном на одинаковом уровне, с пролетом l и при
стреле провисания кабеля f.
Площадь стальной части кабеля Fс,
алюминиевой Fа, объемные веса и модули
упругости равны соответственно 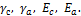
Ответ:
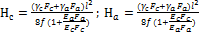 .
.
Задача 10.
Стальной
канат, свитый из 133 проволок диаметром 4 мм, подвешен со стрелой провисания 2
м к опорам, расположенном на одном уровне на расстоянии l=100 м.
Какую равномерно распределенную (вертикальную) нагрузку можно приложить к
канату, если расчетное усилие для каната Трасч=1МН,
вес 1 м каната 142Н, Е=170 ГПа.
Ответ:
q=2,12 кН/м.
Задача 11.
Определить
натяжение в нижнем сечении несущего троса, поддерживающего провод электрической
железной дороги при уклоне i=3%, пролете l=75 м и нагрузке q=16 Н/м троса. Расстояние по вертикали наиболее пониженной точки
троса от вершины более высоко расположенной опоры равно f=3м.
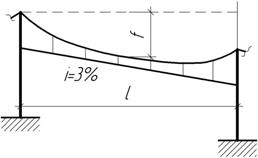
Ответ:
Н=6,67 кН
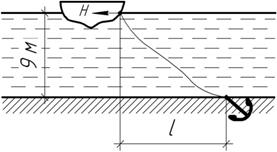
Задача 12.
Плавающая в воде баржа передает на якорную цепь горизонтальное
усилие Н=360 кН. Полная длина цепи 45 м, а
вертикальное расстояние от точки прикрепления цепи к барже до дна равно 9 м.
Погонный вес цепи в воде равен 500 Н/м. Определить горизонтальное расстояние
между якорем т точкой подвеса цепи к барже.
Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
![]() Наружный диаметр цилиндра D=40 мм, внутренний
диаметр d=30
мм. Определить величину сжимающей силы и напряжения в стержне, если модуль
упругости материала равен
Наружный диаметр цилиндра D=40 мм, внутренний
диаметр d=30
мм. Определить величину сжимающей силы и напряжения в стержне, если модуль
упругости материала равен ![]()
![]()
![]() Внутренний диаметр цилиндра d=160 мм, давление газов
в цилиндре р=70 атм, число
шпилек z=14.
Внутренний диаметр цилиндра d=160 мм, давление газов
в цилиндре р=70 атм, число
шпилек z=14.![]() а напряжение не должно быть больше
а напряжение не должно быть больше ![]()
![]() Вычислить нормальное напряжение, абсолютное и
относительное удлинение полосы.
Вычислить нормальное напряжение, абсолютное и
относительное удлинение полосы.![]()
![]()
![]() а удельный вес равен γ=16 кН/м3?
а удельный вес равен γ=16 кН/м3?![]()
![]() в
каждой из колонн? Зависит ли отношение напряжений от величины нагрузки? Модули
продольной упругости арматуры и бетона соответственно равны Еа=200
ГПа и Еб=20 ГПа.
в
каждой из колонн? Зависит ли отношение напряжений от величины нагрузки? Модули
продольной упругости арматуры и бетона соответственно равны Еа=200
ГПа и Еб=20 ГПа.![]()


![]() и поперечного
и поперечного ![]() Эти показания соответствовали возрастанию
нагрузки F на 72 кН. Чему
равны значения модуля Юнга и коэффициента Пуассона материала образца?
Эти показания соответствовали возрастанию
нагрузки F на 72 кН. Чему
равны значения модуля Юнга и коэффициента Пуассона материала образца? ![]()

![]()

![]()
![]() закон изменения которого показан на рисунке. Построить эпюру
напряжений, возникающих в поперечном сечении стержня
при его осевом растяжении силами F.
закон изменения которого показан на рисунке. Построить эпюру
напряжений, возникающих в поперечном сечении стержня
при его осевом растяжении силами F.

![]()
![]() ,
требуется определить величину силы F.
,
требуется определить величину силы F.


![]()

![]()

![]()

![]()

![]()

![]()

![]()
![]()


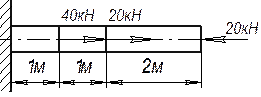
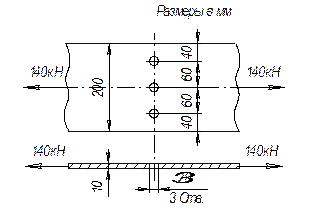
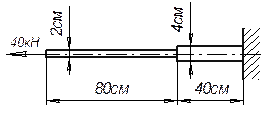


![]()

![]()