Главная
Лекция 20 (продолжение). Задачи
для самостоятельного решения
Задача 1.
Определить допускаемый изгибающий момент при
расчете по предельному состоянию для двутавровой стальной балки I №20,
принимая запас прочности 
Предел текучести принять равным 
Сравнить его с допускающим изгибающим
моментом, рассчитанным по допускаемому напряжению в опасной точке при том же
запасе прочности.
Ответ: Мсr=3,33 кНм; Мmax=2,9 кНм
Задача 2.
Сравнить массы двух сплошных валов
одинаковой длины, подобранных с одинаковым коэффициентом запаса 
если первый вал подбирался по предельному
состоянию, а второй – по допускаемым напряжениям. Крутящий момент Т=10 кНм, предел текучести материала 
.
Ответ: 
Задача 3.
Построить эпюру касательных напряжений
вдоль радиуса, соответствующих предельному состоянию стальной трубы сечением
70х50 мм, и найти предельный крутящий момент, если предел текучести материала 
(Принять
диаграмму Прандтля).
Ответ: Мcr=4,3 кНм
Задача 4.
Сплошной вал круглого сечения диаметром D=5 см закручивается моментами,
приложенными к его концам. Построить эпюру касательных напряжений по радиусу
сечения, соответствующую предельному состоянию вала, и найти предельный
крутящий момент, если предел текучести материала вала 
(Принять диаграмму Прандтля).
Ответ: Мcr=4,9 кНм
Задача 5.
Сравнить величины предельных нагрузок для
двух одинаковых брусьев: защемленного верхним концом и защемленного двумя
концами. Обу бруса нагружены вертикальной силой,
приложенной посредине их длины. Материал брусьев имеет равные пределы текучести
при растяжении и сжатии.
Ответ: 
Задача 6.
Для таврового сечения рассчитать по
предельному состоянию величину в по
следующим данным М=1 кНм, 
(запас прочности).
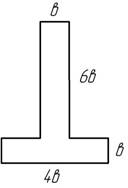
Ответ: в=7 мм
Задача 7.
Найти минимальную величину коэффициента
запаса, который при расчете фермы по предельному состоянию обеспечивает работу
ее стержней в упругой области. Сечения всех стержней одинаковы, F=4 см2; предел текучести , 
предел упругости , 
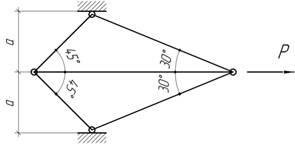
Ответ: Рcr=437 кН, n=1,17
Задача 8.
Найти величину предельной нагрузки Рcr,
приложенного к симметричному пятистержневому узлу.
Площади сечений всех стержней одинаковы, А=2 см2.
Построить график перемещений узла А в функции нагрузки
Р. Дано: l=1 м, 
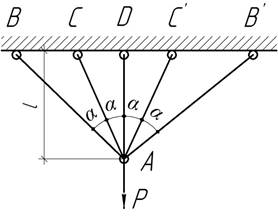
Ответ: Рcr=219 кН
Задача 9.
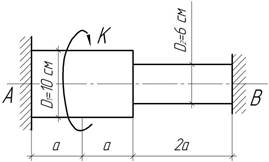
Найти предельную нагрузку для сплошного вала,
защемленного двумя концами и нагруженного посередине сосредоточенным
закручивающим моментом К. Предел текучести материала вала 
диаметр вала D=4 см. Определить, как изменится
предельный момент К, если убрать одну из концевых
заделок.
Задача 10.
1) Определить предельную нагрузку Fu для стержневой системы, показанной на рис.1. Материал стержней АВ и СD имеет предел текучести σy= 285 МПа, балка АС – абсолютно жесткая. Площади поперечных сечений стержней АВ и СD одинаковы и равны А = 5∙10-4 м2.
2) Определить предельную нагрузку Fu для стержневой системы, показанной на рис. 2, если А1 = 2 см2, А2 = 1 см2, предел текучести материала стержней σy = 285 МПа.
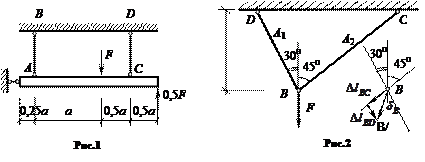
Ответ к рис.1: Fu = 2σyА = 285 кН.
Ответ к рис.2: Fu = 55 кН.
Задача 11.
Определить предельную нагрузку Fu для стержневой системы, изображенной на рисунке. Предел текучести материала стержней σy.
Ответ: Fu = min{Fu1; Fu2}; Fu1 = σy A1cos(α1+α2-90°)/cosα1; Fu2 = σy A2cos(α1+α2-90°)/cosα2.
Задача 12.
Дана плоская шарнирно-стержневая система, состоящая из абсолютно жесткого бруса ВD, опертого на шарнирную опору О (см. рис.). Брус BD прикреплен к двум стержням BB1 и CC1 при помощи шарниров. Площади поперечных сечений стержней ВВ1 и СС1 принять равными А. Предел текучести материала стержней ВВ1 и СС1 – σy. Определить предельную нагрузку Fu.
Ответ: Fu=Aσy.
Задача 13.
Три стержня с одинаковыми площадями поперечных сечения А прикреплены шарнирно к абсолютно жесткой балке ВС (см. рис.). Обозначив предел текучести материала стержней через σy, определить предельную нагрузку Fu.
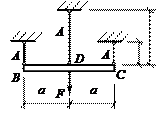
Ответ: Fu=3Aσy.
Задача 14.
Определить предельную нагрузку Fu для стержневой системы, представленной на рисунке. При расчете принять предел текучести материала стержней σy= 2900 кг/см2, брус BD – абсолютно жесткий.
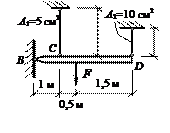
Ответ: Fu = 67,67 т = 663,8 кН.
Задача 15.
1) Определить предельную нагрузку Fu для системы, изображенной на рис. 1. Система состоит из четырех стальных стержней, нижние концы которых соединены общим шарниром. Площади поперечных сечений всех стержней одинаковы и равны А = 4 см2. Предел текучести стали принять σy = 2900 кг/см2.
2) Определить предельную нагрузку Fu для стержневой системы, показанной на рис. 2. Площади поперечных сечений заданы и равны А1 = 5,5 см2; А2 = 2,2 см2; А3 = 3 см2, а предел текучести стальных стержней σy = 250 МПа.
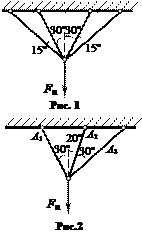
Ответ к рис.1: Fu = 36,496 т = 358 кН.
Ответ к рис.2: Fu = 212,7 кН.
Задача 16.
Абсолютно жесткая балка СD подвешена на трех стальных стержнях, площади поперечных сечений которых равны А1 =1 см2; А2 = 2 см2; А3 = 3 см2 (см. рис.). Предел текучести стали принять σy = 285 МПа. Определить предельную нагрузку Fu.
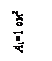
Ответ: Fu = min{152; 171; 228}=152 кН.
Задача 17.
Консольная балка длиной l = 2 м на свободном конце нагружена сосредоточенной силой Fu. Приняв σy = 285 МПа, определить предельную нагрузку Fu, если балка имеет постоянное по длине прямоугольное поперечное сечение h×b = 15 см×5 см.
Ответ: Fu = 40,08 кН.
Задача 18.
Однопролетная шарнирно опертая балка из двутавра №20 нагружена посередине пролета силой F. Пролет балки l = 4 м, предел текучести материала балки Ryn = 285 МПа, расчетное сопротивление стали Ry = 240 МПа, γc= 1. Определить допускаемую Fadm и предельную нагрузку Fu.
Ответ: Fadm = 44,16 кН; Fu = 59,28 кН.
Задача 19.
Для статически неопределимой балки, изображенной на рисунке, найти предельную нагрузку, если предел текучести материала балки Ryn = 285 МПа, а балка представляет собой двутавр № 20, причем l1 = l2 =l = 2 м.
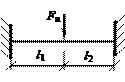
Ответ: Fu = 4Мu/l = 118,56 кН.
Задача 20.
Для статически неопределимой балки, изображенной на рисунке, найти предельную нагрузку, если предел текучести материала балки σy= 285 МПа. Балка имеет прямоугольное поперечное сечение h×b= 0,2 м×0,1 м, а l1 = 1 м, l2 = 2 м.
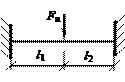
Ответ: Fu = 3Mu = 855 кН.
Задача 21.
Для балки, показанной на рисунке, найти
предельную нагрузку, если предел текучести материала балки Ryn =
285 МПа, балка представляет собой двутавр № 20,
причем l1 = l2 = l = 2 м.
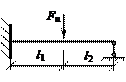
Ответ: Fu = 3Mu /l = 88,92 кН.
Задача 22.
Для один раз статически неопределимой балки, изображенной на
рисунке, найти предельную нагрузку, если предел текучести материала балки
= 285 МПа. Балка имеет прямоугольное поперечное сечение h×b= 0,2 м×0,1 м, а l1 = 1 м, l2 = 2 м.
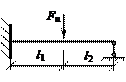
Ответ: Fu = Mu(2 + l1/l2)/l1 = 2,5Mu = 712,5 кН.
Задача 23.
Определить предельную нагрузку для балки
постоянного сечения, показанной на рисунке, если l1 = l2 = l, EIz = const по всей длине балки, – предел текучести
материала балки, Wz,pl
– пластический момент сопротивления.
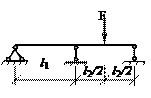
Ответ: Fu = 6σyWz,pl/l = 6Mu/l.
Задача 24.
Стальной стержень сплошного круглого сечения, жестко закрепленный с обоих концов, нагружен крутящим моментом Мu = 50 кНм (рис. а). Определить необходимый диаметр стержня, используя расчет по предельному состоянию. Принять предел текучести материала стержня τy = 150 МПа, коэффициент запаса прочности n = 2.
Ответ: 
Задача 25.
Стальной стержень сплошного круглого сечения жестко закреплен с одного конца, а на другом свободном конце нагружен крутящим моментом Мu = 50 кНм. Определить необходимый диаметр стержня, используя расчет по предельному состоянию. Принять предел текучести материала стержня τy = 150 МПа, коэффициент запаса прочности n = 2.
Ответ: d = 0,137 м.
Задача 26.
Стальной стержень кольцевого сечения с наружным диаметром D = 10 см и внутренним диаметром d = 9 см жестко защемлен с одного конца, а на другом свободном конце нагружен крутящим моментом Мu. Определить предельный внешний крутящий момент Мu, если предел текучести материала стержня τy = 150 МПа.
Ответ: Мu = 10,64 кНм.
Задача 27.
Стальной стержень кольцевого сечения с внутренним диаметром d = 9 см жестко защемлен с одного конца, а на другом свободном конце нагружен крутящим моментом Мu = 10 кНм. Определить наружный диаметр D кольцевого сечения, при котором во всех сечениях кольцевого стержня будет предельное состояние. Предел текучести материала стержня τy = 150 МПа.
Ответ: D = 9,94 см.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
