Главная

Перемещения балок при изгибе

- Две консольные балки равного сопротивления имеют одинаковое квадратное сечение в защемлении и нагружены одинаковыми силами на свободном конце. У первой балки меняется ширина, у второй – высота. Какая балка будет легче? У какой из них наибольший прогиб будет больше?

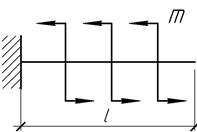
- Балка длиной 2а изогнута по кривой, отвечающей уравнению

Определить внешние силы, действующие на балку. Построить эпюры изгибающего момента и поперечной силы.

- Балка пролетом 1 м, свободно лежащая на двух шарнирных опорах, изогнута по дуге окружности. Сечение балки прямоугольное со сторонами в=6 см и h=4 см. прогиб, измеренный посередине, оказался равным f=6,25 мм. Определить величину модуля упругости материала балки и радиус кривизны оси при условии, что наибольшее напряжение в балке равно

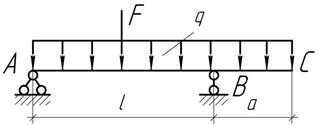
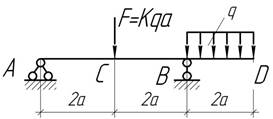
- Какую силу F нужно приложить посередине пролета АВ в дополнение к погонной нагрузке q=30 кН/м, чтобы прогиб конца равнялся нулю, если l=3 м, а=2 м?

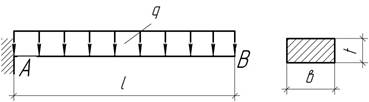
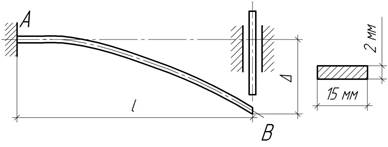
- Стальная полоса длиной l=10 см и толщиной t=2 мм испытывает действие погонной нагрузки q=160 Н/м. Определить ширину полосы в из условия, что максимальный угол поворота равен 10 мрад. При найденном значении в вычислить наибольший прогиб и максимальное напряжение изгиба.

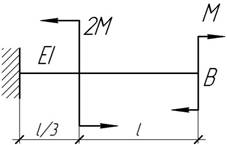
- При каком отношении М₁/М₂ угловое перемещение левого торца балки будет равно нулю?

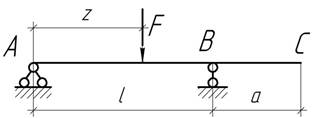
- Какому положению подвижной нагрузки F соответствует наибольший прогиб сечения С?

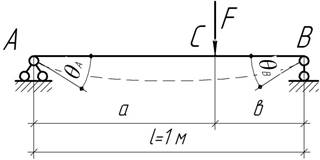
- Найти точку приложения силы F, если отношение углов поворота на опорах .

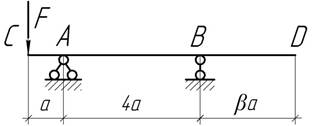
- При каком значении коэффициента β прогибы концов балки будут одинаковы?

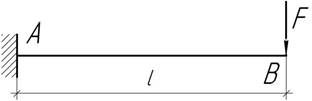
- Балка симметричного сечения высотой h=20 см и длиной 2 м изгибается под действием силы F, вызывающей наибольшие напряжения, равные Найти прогиб и угол поворота на свободном конце, пологая Е =100 ГПа.

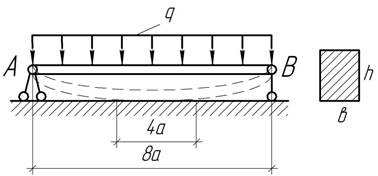
- При какой нагрузке q стальная балка прямоугольного сечения 6х10 см и длиной 8 м, опирающаяся на шарнирные опоры высотой будет иметь касание на половине ее длины с абсолютно жестким основанием. Чему равны в этом случае наибольшие нормальные напряжения?

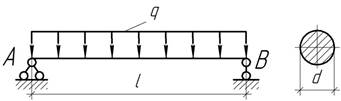
- Наибольший прогиб балки круглого сечения диаметром d=100 мм и длиной l=4 м равен f=20 мм. Определить максимальное напряжение и углы поворота на опорах, пологая Е =100 ГПа.

- При каком значении жесткости пружины С изгибающий момент в заделке будет равен нулю?

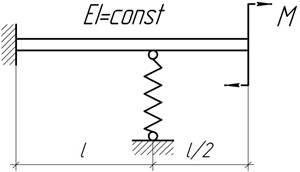
- При каком соотношении моментов инерции I₁ и I₂ участков АВ и ВС стальной балки, максимальное перемещение будет иметь место в сечении, где приложена нагрузка F? Найти это перемещение V, если F=6250 Н, l=0,24 м,

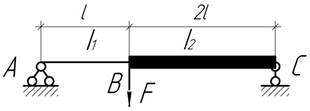
- На каком расстоянии а от средней опоры нужно приложить момент М, чтобы балка на левом пролете оставалась прямой? Изгибная жесткость EI балки постоянна.

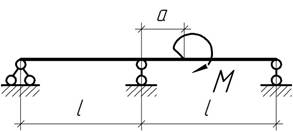
- Шарнирно опертая по концам стальная балка длиной 1 м нагружена моментами М=100 Нм. Найти наибольший прогиб, углы поворота на опорах и горизонтальное смещение подвижной опоры.

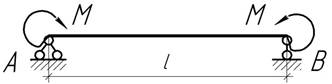
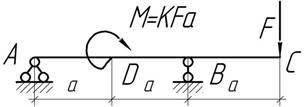
- При каком значении коэффициента К прогиб сечения с равен нулю? Чему равен угол поворота этого же сечения?

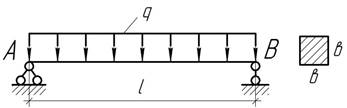
- Шарнирно опертая по концам балка квадратного сечения длиной 4 м испытывает действие погонной нагрузки q=8 кН/м. определить максимальный прогиб балки и радиус кривизны в ее среднем сечении, если наибольшее напряжение изгиба равно 12 МПа и модуль упругости Е=10 ГПа.

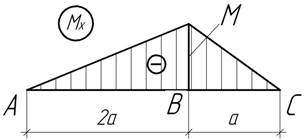
- По заданной эпюре изгибающего момента определить угол поворота сечения С балки, если прогибы в сечениях А и В равны нулю, жесткость балки постоянна и равна EI_х=200 кНм², а=1 м, М=2,4 кНм.

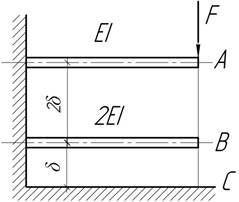
- Определить силу F, при которой концы балок А и В коснуться точки поверхности С.

- Плоская стальная пружина длиной l=10 см должна прижать деталь с силой 30 Н. определить прогиб и угол поворота свободного конца пружины, а также наибольшее напряжение изгиба.

- Какую силу F можно приложить в дополнение к погонной нагрузке q=6 кН/м, чтобы наибольшие нормальные напряжения не превышали 160 МПа, а наибольший прогиб не превосходил 1/250 пролета балки l=2 м.

- Определить модуль упругости материала балки, радиус кривизны в сечении А и угол поворота на свободном конце, если и прогиб в точке В равен

- Определить коэффициент К, при котором прогиб сечения D равен нулю. Чему при этом равен прогиб под силой F?

- При действии момента М=100 Нм, касательная и упругой линии балки на свободном конце составляет угол Определить модуль упругости материала балки, радиус кривизны оси, прогиб в точке В и наибольшее напряжение изгиба.

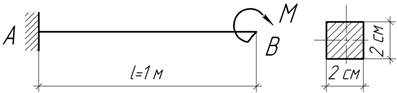
- Стальная двутавровая балка №20 длиной 4 м нагружена сосредоточенным моментом, вызывающем наибольшее напряжение изгиба, равные 100 МПа. Определить величину момента М, радиус окружности, по которой изгибается балка и прогиб на свободном конце.

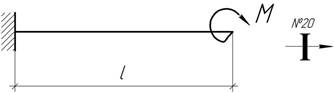
- Какую силу F надо приложить к свободному концу балки АВ, нагруженным собственным весом, чтобы суммарное перемещение сечения В было равно нулю. Погонный вес балки q, изгибная жесткость EI и длина l известны.

- При какой длине консоли а угол поворота на опоре В равен нулю? Чему равен в этом случае прогиб на конце консоли?

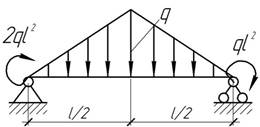
- Для трехопорной балки заданы эпюра изгибающего момента. Определить величину неизвестного момента М?

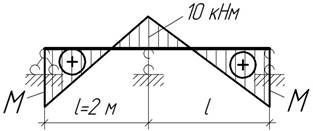
- Ось балки длиной 2а изогнута по кривой, отвечающей уравнению Определить внешние силы, действующие на балку, и положение опор; построить эпюры поперечной силы и изгибающего момента.

- Закон изменения распределенной нагрузки . Составить выражение для поперечной силы и изгибающего момента, найти перемещение свободного конца консоли.

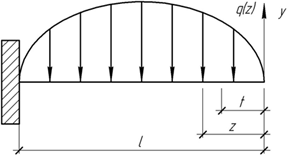
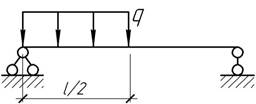
- Определить прогиб и угол поворота для среднего сечения балки.

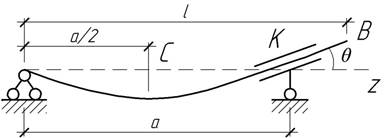
- Балка постоянного сечения закреплена на двух опорах. Левая опора - шарнирно неподвижная, правая (К) – в виде короткой трубки, которая под малым углом наклонена к оси z и может свободно перемещаться вдоль этой оси, изгибая балку. При каком а прогибы в точках В и С будут равны по абсолютному значению? Трением между втулкой и балкой пренебречь. В пролете балка не нагружена.

- При каком отношении a/l будет минимально: а) величина максимального прогиба; б) величина максимального изгибающего момента?

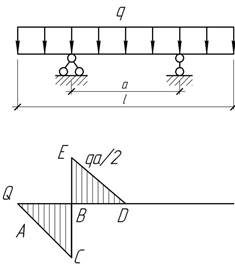
- Найти при каком соотношении b/a отсутствует изменение длины верхних и нижних волокон балки постоянного сечения.

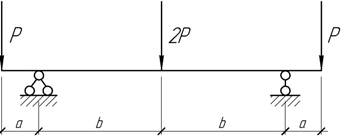
- Для балки, нагруженной в сечениях А и В, требуется экспериментально найти изогнутую ось. Как это сделать с наименьшим числом перестановок одного индикатора?

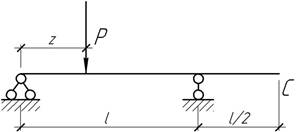
- Определить при каком значении z прогиб в сечении С будет наибольшим.

- Консольная балка жесткостью EI и длиной l на конце нагружена парой сил с моментом М=3EI/l. Найти вертикальное перемещение концевого сечения В балки.

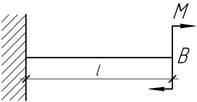
- Брус АВ, погонный вес которого равен q, свисает с абсолютно жесткой плиты на 1/3 своей длины. Определить вертикальное перемещение свисающего конца бруса.

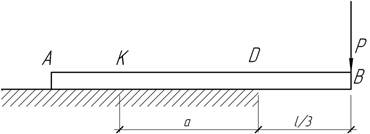
- Полоса (жесткость EI) расположена между жесткими плитами с зазором δ и изгибается силами Р на консолях. Определить величины нагрузок: Р₁ – при которой полоса коснется верхней плиты, Р₂ – при которой начнется прилегание полосы к верхней плите, Р₃ – при которой полоса приляжет к верхней плите на участке длиной 2t, а также вертикальные перемещения концов консолей при Р>Р₂.

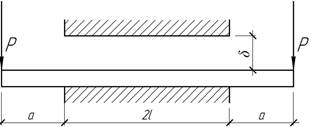
- Для составной балки круглого поперечного сечения (Е₁=8Е₂), изгибаемой парами сил с моментами М, установить законы изменения нормальных напряжений в ее частях и определить угол взаимного поворота концевых сечений.

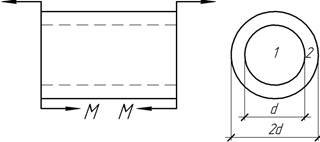
- Момент m равномерно распределен по длине балки. Определить прогиб на конце консоли.

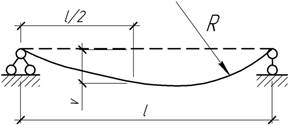
- Определить прогиб v середины пролета балки, у которой левая половина оси прямая, а правая изогнута по дуге окружности радиуса R.

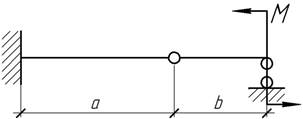
- При каком соотношении размеров а и b изогнутая ось балки не будет иметь излома в шарнире?

- Уравнение упругой линии стержня имеет вид Установить действующие на стержень силы и характер закреплений.

- Пластинка сделана из упругого изотропного материала с модулем упругости Е и коэффициентом Пуассона ν. Вычислить изменение площади лицевой поверхности пластинки, полагая, что последняя находится в плоском напряженном состоянии. Указания. Воспользоваться теоремой взаимности работ после приложения равномерно распределенного давления к боковой поверхности пластинки.

- Консольная балка жесткостью EI нагружена парами сил с моментами 2М и М=πEI/l. Найти вертикальное перемещение концевого сечения В.

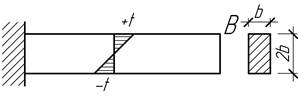
- Температура по высоте балки меняется по линейному закону от +t до –t. Найти вертикальное перемещение сечения В.

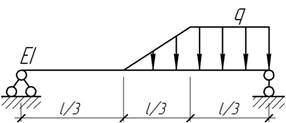
- Определить прогиб балки в середине пролета.

- Установить, на каком расстоянии следует установить правую опору, чтобы прочность балки по нормальным напряжениям была наибольшей.

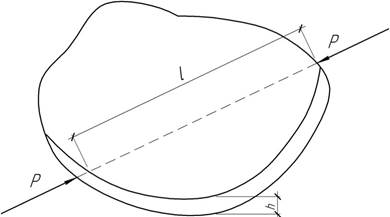
- Вычислить изменение длины отрезка АВ.

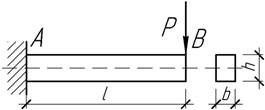
- При какой длине консоли прогибы балки в сечениях С и D одинаковы по абсолютной величине?

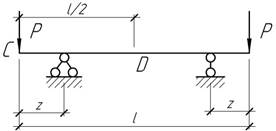
- Определить прогиб в середине пролета балки.

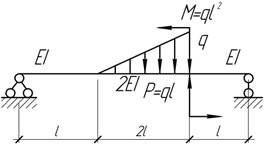
- Определить угол, на который надо повернуть сечение А, чтобы при нагружении балки силой Р угол поворота сечения В был равен нулю.

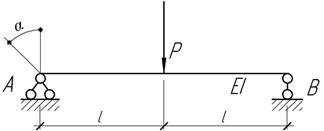
- Принимая Δ=l/100, установить, при каком значении М концы бруса коснуться опор А и В.

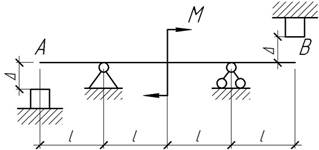
- Балка длиной l, шарнирно опертая по концам, несет нагрузку от собственного веса. Как изменится прогиб и максимальные нормальные напряжения в балке, если все размеры балки увеличить в n раз?

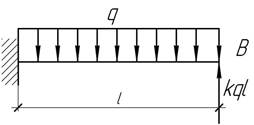
- Определить значение коэффициента К, при котором прочность балки будет максимальной. На какую величину надо переместить по вертикали шарнирную опору (вверх или вниз), устанавливаемую в сечении В вместо силы kql, чтобы достигался тот же эффект?

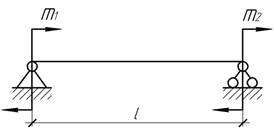
- Балка с шарнирно закрепленными концами изгибается моментами . Определить отношение если точка перегиба балки находится на расстоянии 2l/3 от правой опоры.

- Определить угол поворота в середине сечения балки. Принять EI=const.

- При каком соотношении сил F₁ и F₂ линейные перемещения точек их приложения будут одинаковыми, если жесткость консольной части балки в два раза больше жесткости сечения в пролете?

- При каком отношении I₁/I₂ вертикальное перемещение балки в точке приложения силы F будет максимальным? Найти величину этого перемещения в общем виде.

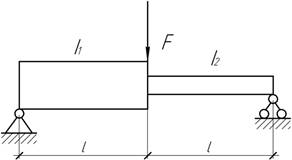
- При каком отношении l₁/l₂ вертикальное перемещение точки К балки будет максимальным? Найти величину этого перемещения в общем виде.

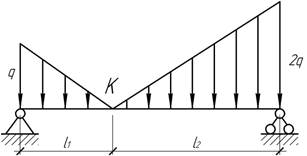
- Определить вертикальное положение середины бруса, если ширина ослабленного сечения равна а и модуль упругости Е. Высота сечения и длина бруса показаны на рисунке.

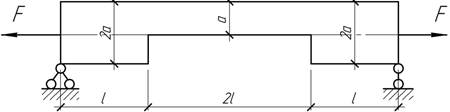
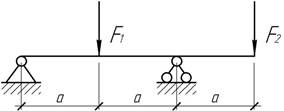
- При каком отношении сил F₁ и F₂ вертикальное перемещение правого конца балки равно нулю? (EI=const).

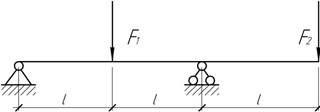
- Определить горизонтальное перемещение точки С в общем виде. Известны: Е, а, l, q.

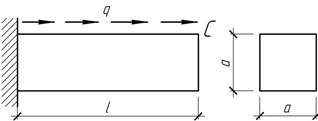
- Приняв определить, при каком отношении I₁/I₂ вертикальное перемещение сечения, где приложен изгибающий момент М, равно нулю. Чему равен при этом угол поворота сечения?

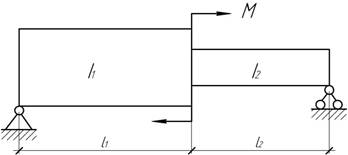
- При какой длине х правой консоли прогибы левой и правой концов балки будут равны? Жесткость балки EI=const, a=l/4.

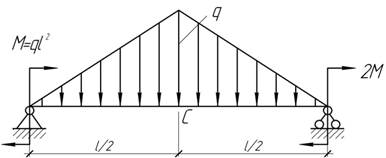
- Определить угол поворота среднего сечения С балки, если EI=const, M=ql².

- Какую форму должна иметь балка прямоугольного сечения постоянной высоты h и переменной ширины b, чтобы ее ось изгибалась по дуге окружности?

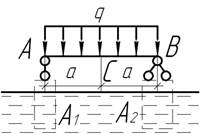
- Опоры А и В опираются на понтоны, площади основания которых равны А₁ и А₂. Чему равно перемещение сечения С от нагрузки, если удельный вес воды равен γ?

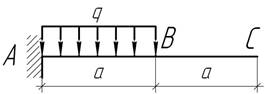
- Зная что для консоли, загруженной по всей длине l равномерно распределенной нагрузкой q, прогиб на свободном конце равен а угол поворота определите из геометрических соображений прогиб и угол поворота сечения С для данного случая.

- Требуется экспериментально определить угол поворота сечения С. Однако конструкция экспериментальной установки позволяет нагружать балку в любом сечении, а углы поворота замерять только на опорах. Как замерить искомый угол?

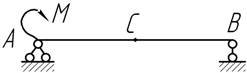
- При нагружении балки моментами М наибольшие нормальные напряжения равны допускаемому [σ]. Какая энергия накоплена балкой?

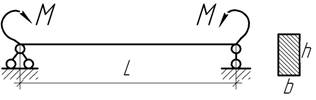
- Используя теорему Кастилиано, определите угол поворота сечения В.

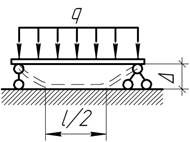
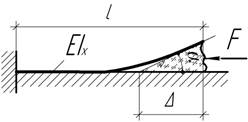
- Определить, при какой нагрузке q балка жесткостью EI_x, опирающаяся на шарнирные опоры высотой Δ, будет иметь сплошное касание на длине l/2 с абсолютно жесткой плитой?

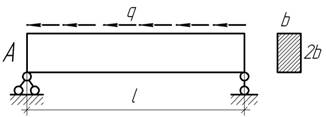
- Определите угол поворота сечения А балки. Дано: q, b, l, E.

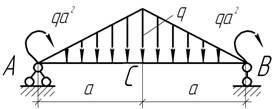
- Определить угол поворота в сечении С балки.

- Гибкий стержень лежит на абсолютно жесткой плоскости. При каком минимальном отношении b/а стержень касается плоскости лишь в двух точках А и В?

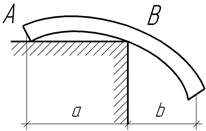
- При заданных величинах а и b определите, при каком отношении моментов инерции I₁:I₂ линейное перемещение сечения, где приложен сосредоточенный момент М, равно нулю? Чему равен при этом угол поворота этого сечения?

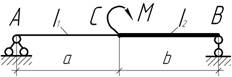
- Длинная гибкая балка жесткостью EI_x лежит на жестком основании и поднимается за середину силой F. Полагая погонный вес балки равным q, определите длину оторвавшейся от основания части а балки.

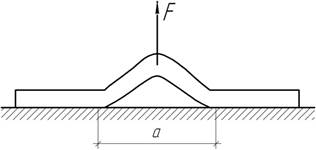
- Клин с малым углом α при вершине перемещается под действием силы F на величину Δ, поднимая коней балки. Установите зависимость F=f(Δ).

- Свободно опертая балка длиной l и высотой h имеет температуру Т₂ на нижней поверхности и Т₁ – на верхней. Исследуйте перемещения сечений балки и определите наибольший прогиб.

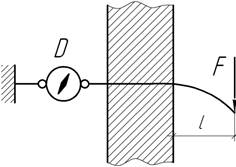
- Упругая балка плотно, но без зазора вставлена в отверстие, высверленное в жестком основании. Интуитивно представляется, что при нагружении поперечной силой F балка выскользнет из заделки. Но непонятно, под действием каких сил? Что покажет динамометр, если силы трения отсутствуют?

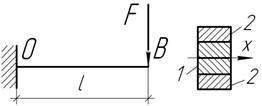
- Определите прогиб и угол поворота свободного конца балки, выполненной из разномодульных материалов. Сечение балки симметрично относительно центральной оси х.

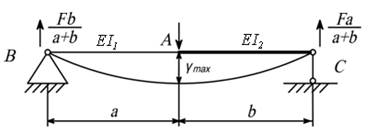
- При каком соотношении моментов инерции I₁/I₂ максимальный прогиб будет достигнут в сечении А?

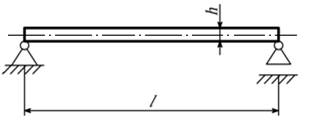
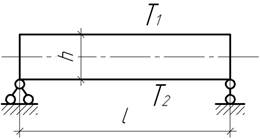
- Изображенная на рисунке балка длиной l=6м и высотой h=40см при первоначальной температуре t₀ имела нулевую кривизну. Определить наибольший прогиб балки при изменении температуры верхних волокон до t₁=-20^°С, а нижних – до t₂=40^°С. Принять, что температуры по высоте балки меняются по линейному закону. Что можно сказать о напряжениях в балке? Принять α=125∙10^-7.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00