Главная
Статически
неопределимые системы
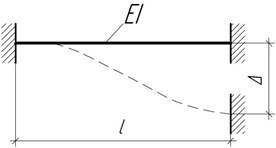
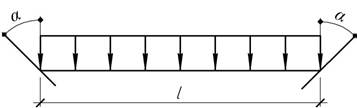
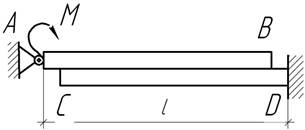
- Концевые сечения балки длиной l
не имеют угловых перемещений. Одна из
опор получает линейное перемещение, равное 
. Считая жесткость балки постоянной, найти угол поворота
среднего сечения.
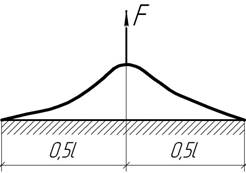
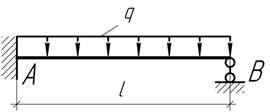
- Длинная гибкая балка жесткостью EI лежит
на жестком основании и поднимается за середину силой F. Определить длину оторвавшейся от основания части
балки, погонный вес которой равен g.
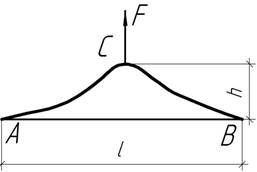
- Длинная труба наружным диаметром d=130 мм и толщиной t=4,9 мм поднимается за середину силой F. Из условия прочности трубы определить максимальную
высоту подъема, длину приподнятой части l и
необходимую величину силы F, если 
.
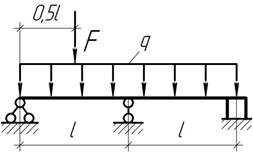
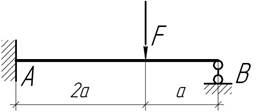
- Какое предельное значение может иметь сила F, чтобы правый конец балки не отвалился от гладкой
опоры?
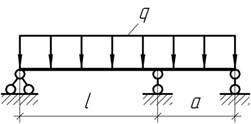
- Как должны относиться пролеты балки l
и а,
чтобы реакция правой опоры оказалась равной нулю?
- На какую высоту нужно поднять опору В балки АВ жесткостью EI, чтобы напряжение в сечении А были равны нулю?
- На сколько нужно сместить опору В,
чтобы сделать равными по абсолютной величине изгибающие моменты в пролете и в
защемлении?
-
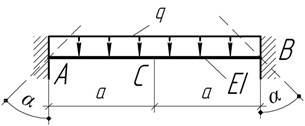
На какие углы α следует при защемлении повернуть концы балки постоянной
жесткости EI, чтобы после приложения
нагрузки q моменты в сечениях А, В и С
были одинаковы?
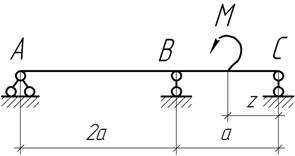
- При каком значении z изгибающий момент под силой F будет максимальным?
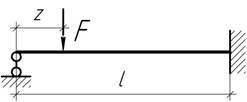
- При каком значении х коэффициент запаса трехопорной балки АВ наибольший? Балка находится в условиях
прямого изгиба, поперечное сечение постоянно, материал одинаково сопротивляется
растяжению и сжатию.
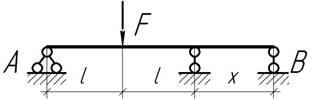
- На какую величину необходимо опустить средние опоры
балки, чтобы изгибающие моменты в сечениях над этими опорами обратились в нуль?
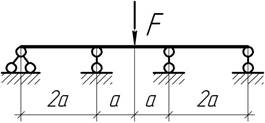
- При каком расстоянии z перемещение в пролете АВ равны
нулю?
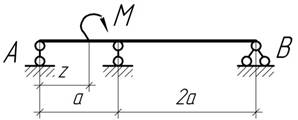
- Задано: q, l, EI. Определить угол α, на который надо повернуть опорные
сечения балки, чтобы нормальные напряжения изгиба были минимальными.
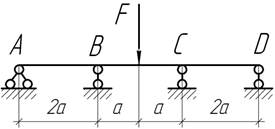
- На какую величину Δ необходимо опустить средние
опоры балки, чтобы изгибающие моменты в сечениях над этими опорами обратились в
нуль?
- На какую величину Δ следует опустить опоры В и С балки, чтобы изгибающие моменты в сечениях над этими
опорами обратились в нуль? Дано: F, EI, a.
- При каком расстоянии z перемещения в пролете АВ равны нулю?
- На какую высоту Δ нужно поднять опору В балки АВ жесткостью EI, чтобы напряжения в сечении А были равны нулю?
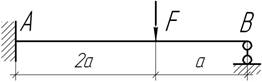
- При какой величине Δ изгибающий момент в
сечении С равен нулю? Дано: F, EI, a.
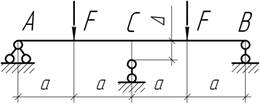
- Треугольная призма из хрупкого материала опирается
концами на 2 катка (рисунок а). почему опирание
на 3 катка (рисунок б) при их грубом изготовлении или плохом основании более
опасно для прочности призмы? Заметим, что ответ на этот вопрос волновал еще
древних греков, на практике убедившихся в опасности хранения мраморных призм на
трех катках.
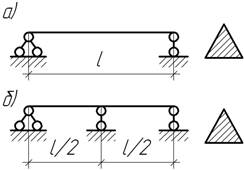
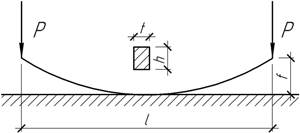
- На абсолютно жестком основании лежит полоса
прямоугольного сечения bxh. Определите, на какой длине а полоса приподнимается над плоскостью
при приложении к ее концу силы F. Определите
прогиб f. Удельный вес материала полосы γ.
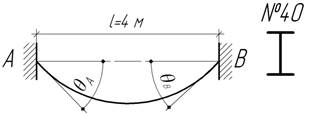
- Стальная двутавровая балка № 40 с прямолинейной
продольной осью изогнута, а после этого закреплена своими концами в неподатливые
опоры, так что 
После заделки концов внешняя нагрузка с балки снята. Чему равны
наибольшие напряжения в балке?
- В каком сечении возникает наибольший изгибающий
момент и чему он равен?
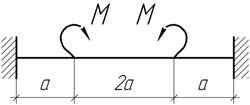
- При нагружении балки моментом на
правой опоре правое сечение получило угловое перемещение θ. Найти угловое
перемещение сечения, в котором кривизна оси стержня равна нулю.
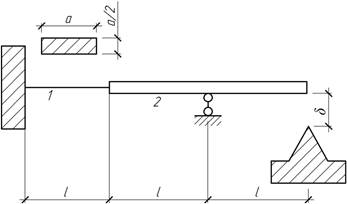
- Найти наибольшее нормальное напряжение в поперечном сечении
стержня 1 после закрытия зазора δ. Деформациями правого стержня 2
пренебречь. Дано: l, a,
δ, E.
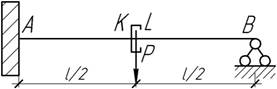
- Балка состоит из двух частей: AK и
LB. Торцевые сечения K
и L
не могут поворачиваться относительно друг друга. К сечению L
приложена сила Р. Построить
эпюру изгибающих моментов. Определить относительное смещение сечений K и
L и
изобразить изогнутую ось балки.
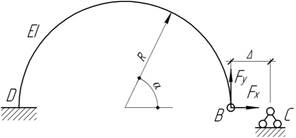
- Концевое сечение В соединяется с
неподвижным шарниром С. Найти изгибающий момент в сечении D.
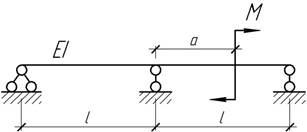
- На каком расстоянии от средней опоры надо приложить момент,
чтобы балка в левом пролете осталась прямой?
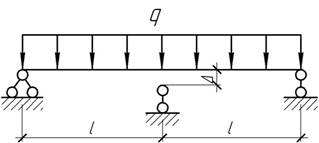
- Подобрать зазор на средней опоре таким, чтобы вес балки был
наименьшим.
- Полубесконечная балка жесткостью EI и погонного веса q лежит на абсолютно
жестком основании. Определить, на какой длине z балка оторвется от
основания. Вычислить прогиб конца балки.
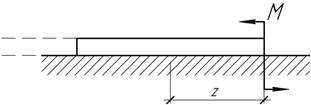
- Стержень постоянного сечения жестко защемлен левым концом. До нагружения его ось слабо искривлена по уравнению у=kz3. Определить длину
участка, на котором стержень прилегает к жесткой горизонтальной плите.
- Защемленный стержень нагрет. Закон изменения температуры по
высоте – линейный: Δt=2yT/h. Определить внутренние усилия в сечении и характер искривления
оси стержня.
- Стержень имеет такую первоначальную кривизну, что при
выпрямлении его возникает равномерно распределенное давление. Определить силы Р, необходимые для распрямления, и наибольшие напряжения в
стержне.
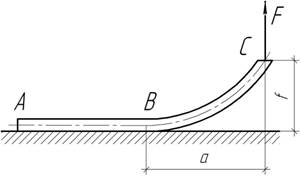
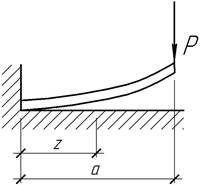
- Найти расстояние а,
при котором удлинение верхнего волокна от собственного веса балки постоянного
сечения отсутствует.
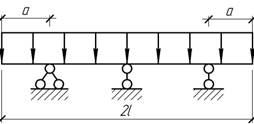
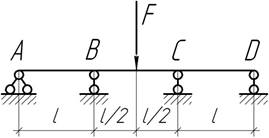
- На какую величину Δ нужно опустить средние опоры балки,
чтобы изгибающие моменты в сечениях под этими опорами обратились в нуль?
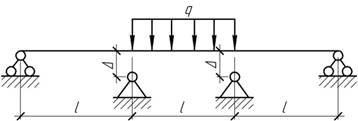
- Двухопорная балка нагружена
распределенной нагрузкой q. На какую величину
Δ надо опустить среднюю опору, чтобы вес балки постоянного сечения был
наименьшим.
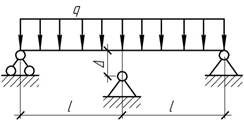
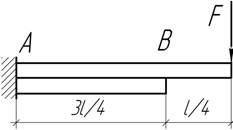
- При каком соотношении сил F1 и F2 линейные перемещения
точек их приложения будут одинаковыми, если жесткость консольной части балки в
два раза больше жесткости сечения в пролете?
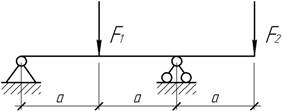
- Средняя опора балки получает случайную осадку 
Как изменятся
максимальные напряжения, если балку сплошного сечения (а) заменить коробчатой формой той же высоты и толщины?
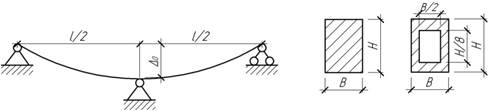
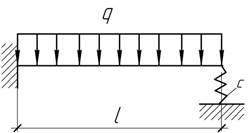
- Балка, нагруженная равномерно распределенной нагрузкой, левым
концом защемлена, а правым опирается на пружину жесткостью с.
Дано: q, l,
c, EI. Определить осадку пружины в общем виде.
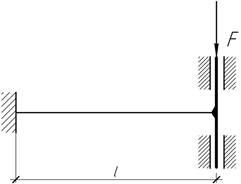
- Левый конец балки жестко заделан, а правый конец помещен в
направляющие так, что может свободно перемещаться в вертикальном направлении,
но не может поворачиваться. Определить вертикальное перемещение правого конца
балки, если EI=const.
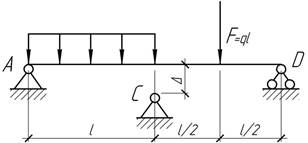
- Двухпролетная балка опирается на три
опоры А, С и D. До приложения
нагрузок на опоре С имеется зазор, равный – Δ.
Чему должен быть равен зазор, чтобы все три реакции на опорах были одинаковы?
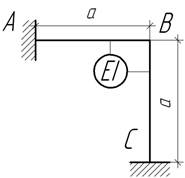
- Горячий нефтепровод образует колено, сечение
которого А и С можно считать защемленными. Определить
величину изгибающего момента в колене, когда по нему течет нефть с температурой
t0. Дано: EI, a, α.
- Концевые сечения балки длиной l не имеют
угловых перемещений. Одна из опор получает линейное перемещение Δ=0,004l. Считая
жесткость балки постоянной, найти угол поворота среднего сечения.
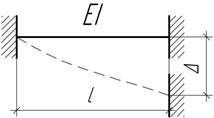
- При установке трех опор балки таврового сечения одна
из них оказывается ниже и выключается из работы: в одном варианте – опора А, в
другом – средняя опора С. Полагая, что предел текучести при сжатии 
в 1,5 раза выше предела
текучести при растяжении 
, сравните коэффициенты запаса в указанных вариантах.
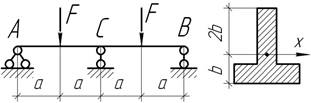
- Абсолютно жесткий брус АВ опирается на пять стержней
разной изгибной жесткости. Под действием горизонтальной силы F он перемещается поступательно, т.е. не
поворачивается. Какие усилия возникают в опорных стержнях? Дано: EI, F, l.
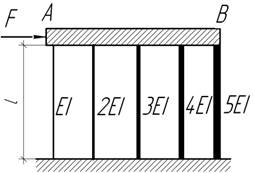
- Определить прогиб сечения С
полубесконечной системы, состоящей из одинаковых
балок длиной l и жесткостью EI.
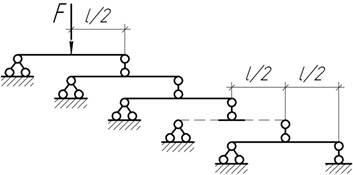
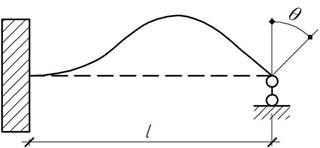
- Найти угол поворота на левой опоре полубесконечной балки постоянной жесткости EI.
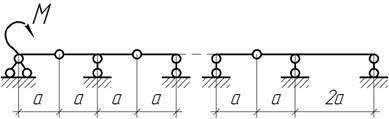
- Через пять равноудаленных роликов одинакового
диаметра d, центры которых лежат на одной
прямой, протянута полоса толщины t=d и постоянной изгибной жесткости по длине ЕI. Определить давление полосы на ролики, если d<<а.
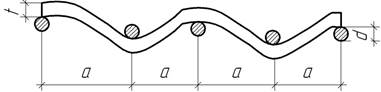
- Две стальные балки жесткостью EI соприкасаются во всех точках до нагружения
и в точках А, В – после нагружения.
Найти максимальную высоту щели, которая образуется между балками под нагрузкой.
Дано: F, EI, l.
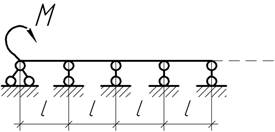
- Построить эпюру изгибающих моментов для полубесконечной нарезной балки,
нагруженной на левом конце моментом М. Все пролеты балки имеют
одинаковую длину l и жесткость EI.
- Стержень АВ шарнирно закреплен в точке А и свободно лежит на балке СД. Построить эпюры изгибающих
моментов в обеих балках от момента М,
приложенного в опоре А. жесткости обеих балок одинаковы и равны EI.
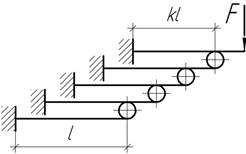
- Установите, как будет передаваться (через
специальные вкладыши) нагрузка F на все виды
балок одинаковой жесткости EI, если k=0,8.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
