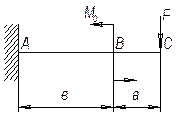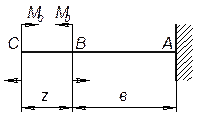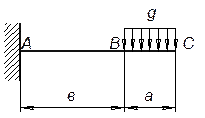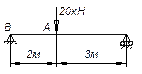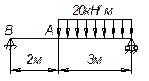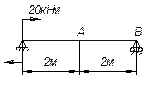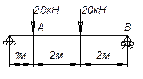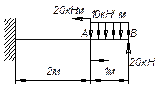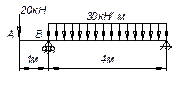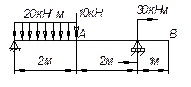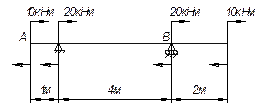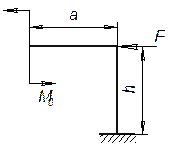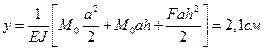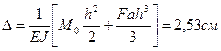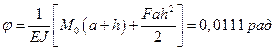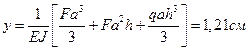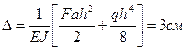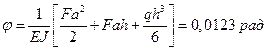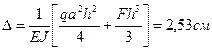Главная
Лекция 13 (продолжение). Задачи для самостоятельного решения
Содержание
Определение перемещений в балках
Определение перемещений в рамах
Определение перемещений в балках
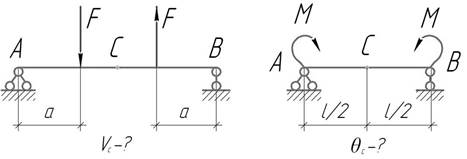
Задача
1.
Свободно опертая балка прямоугольного сечения
под действием равномерно распределенной нагрузки получает прогиб в середине,
равный 5 см. Эта балка заменяется другой балкой из того же самого материала и
так же прямоугольного сечения, но с шириной вдвое меньшей, чем у исходной
балки. Какова должна быть высота новой балки 
по
сравнению с высотой 
исходной балки, если новая балка под действием
той же самой нагрузки прогибается только на 1,25 см?
Задача
2.
Чугунная балка с сечением в виде
равностороннего треугольника нагружается в плоскости его высоты и работает в
положениях, когда основание треугольника лежит в области сжатых волокон и в обратном. В каком из указанных положений получится больший
прогиб?
Задача
3.
Стальная балка квадратного сечения нагружается в плоскости симметрии, параллельной стороне квадрата, а затем в диагональной плоскости. В каком положении прогиб больше?
Задача
4.
Две консольные балки равного
сопротивления имеют одинаковое квадратное сечение в защемлении и нагружены
одинаковыми силами на свободном конце. У первой балки меняется ширина, у второй
– высота. Какая балка будет легче? У какой из них наибольший прогиб будет
больше?
Ответ: G1/G2=f1/f2=3/4.
Задача
5.
Деревянная консольная балка равного
сопротивления постоянной высоты h=12 см и переменной ширины нагружена на
свободном конце силой F=4 кН. Длина
балки l=1,2 м. Какой
должна быть ширина балки в защемлении 
и
наименьшая ширина на свободном конце b при допускаемых напряжениях [σ]=10
МПа и [τ]=1 МПа. На какой длине а от свободного конца должна быть
выдержана наименьшая ширина балки. Определить прогиб свободном конце.
Ответ: 
Задача
6.
Шарнирно опертая по концам стальная балка
равного сопротивления имеет прямоугольного постоянной высоты h=20 см и длину l=4 м. Балка испытывает действие
равномерного распределенной нагрузки интенсивности q=200 кН/м. Принимая [σ]=200 МПа, найти наибольшую ширину балки 
. Вычислить также величину наибольшего
прогиба, предполагая что на опорах
ширина балки сходит на нет.
Ответ: =30 см, f=2 см.
Задача
7.
Балка пролетом 1 м, свободно лежащая на
двух шарнирных опорах, изогнута по дуге окружности. сечение балки прямоугольное со сторонами b=6 см и h=4 см. Прогиб, измеренный посредине
пролета, оказался равным f=6,25 мм. Определить величину модуля
упругости материала балки и радиус кривизны оси при условии, что наибольшее
напряжение в балке равно 
Ответ: Е=10 ГПа, ρ=20 м.
Задача
8.
Две балки прямоугольного сечения,
шарнирно опертые по концам, нагружены сосредоточенными силами в пролете, причем
в обоих случаях точки приложения сил делят длину в одном и том же отношении.
Чему равно отношение наибольших прогибов для этих балок, если наибольшие
нормальные напряжения в обоих случаях одинаковы?
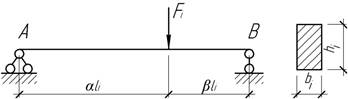
Ответ: 
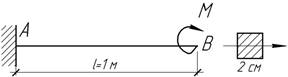
Задача
9.
При действии момента М, равного 100 Нм, касательная к упругой линии балки на свободном конце
составляет угол θв=37,5 мрад.
Определить модуль упругости материала балки, радиус кривизны оси, прогиб в
точке В и наибольшее напряжение изгиба.
Ответ: Е=200 ГПа, ρ=26,7 м; 
см, 
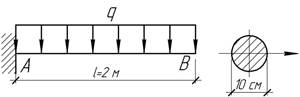
Задача
10.
Определить модуль упругости материала
балки, радиус кривизны в сечении А и угол поворота на
свободном конце, если 
и
прогиб в точке В равен 
см.
Ответ: Е=70 ГПа, 
Задача
11.
Балка симметричного сечения высотой h=20 см и длиной 2 м изгибается под
действием силы F, вызывающей наибольшие напряжения,
равные 
Найти прогиб и угол поворота на свободном
конце, полагая Е =100 ГПа.
Ответ: 
Задача
12.
На верхней поверхности стальной балки
длиной l=60 см на расстоянии
а=20 см от заделки установлен
тензометр. При нагружении балки силой F прогиб под силой составил 
мм. Определить показания тензометра и
наибольшее напряжение в балке.
Ответ: 
Задача
13.
Какую силу F нужно приложить посредине пролета АВ в
дополнение к погонной нагрузке q=30 кН/м, чтобы прогиб конца консоли
равнялся нулю, если l=3 м, а=2
м?
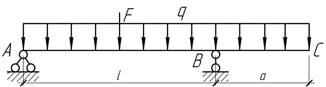
Ответ: F=100 кН.
Задача
14.
Какую силу F можно приложить в дополнение к погонной
нагрузке q=6 кН/м, чтобы наибольшие нормальные
напряжения не превышали 160 МПа, а наибольший прогиб не превосходил 1/250
пролета балки l=2 м.
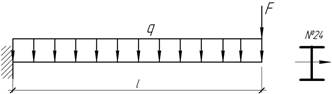
Ответ: F=Fж=16,26 кН.
Задача
15.
К стальной балке, нагруженной силой F посредине, в точке С
прикреплен указатель СД. Найти опускание его конца и угол, образованный
указателем с горизонтальной линией, проходящей через точку С
упругой линии, если F=24 кН, а=1 м, b=12 см, h=10 см.
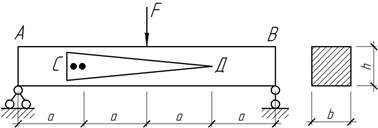
Ответ: Vд=2,9 см, θс=9 мрад.
Задача
16.
Шарнирно опертая по концам балка квадратного
сечения длиной 4 м испытывает действие погонной нагрузки интенсивности q=8 кН/м. Определить максимальный прогиб
балки и радиус кривизны в ее среднем сечении, если наибольшее напряжение изгиба
равно 12 МПа и модуль упругости материала Е=10 ГПа.
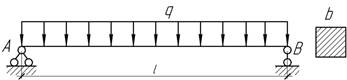
Ответ: f=2 см, ρ=250/3 м.
Задача
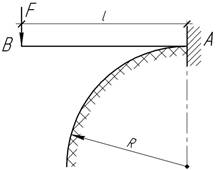
17.
Один конец стальной балки жестко
закреплен на неподвижной опоре, а другой жестко заделан в
ползун, который может перемещаться по окружности
радиуса R=l. Определить наибольшее напряжение в
балке, а также прогиб и угол поворота концевого сечения В,
если F=1,5 кН, R=0,5 м.
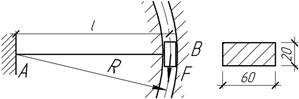
Ответ: 
Задача
18.
В результате погрешности монтажа ось
крайнего подшипника трехопорного стального вала
диаметром d=200 мм оказалось расположенной ниже осей
двух других опор на величину Δ=1,5 мм. Определить силы, действующие на
каждую из опор, а также максимальное нормальное напряжение.
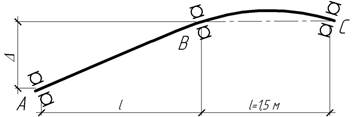
Ответ: 
Задача
19.
Стальная полоса длиной l=10 см и толщиной t=2 мм испытывает действие погонной
нагрузки q=160 Н/м. Определить ширину полосы b из условия, что максимальный угол поворота
равен 10 мрад. При найденном значении b вычислить наибольший прогиб и
максимальное напряжение изгиба.
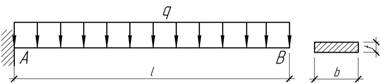
Ответ: b=20 мм, f=0,75 мм, 
Задача
20.
Шарнирно опертая по концам стальная балка
длиной 1 м нагружена моментами М=100 Нм. Найти
наибольший прогиб, углы поворота на опорах и горизонтальное смещение подвижной
опоры.
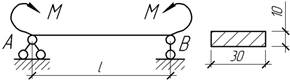
Ответ: f=25 мм, 
Задача
21.
Наибольший прогиб балки круглого сечения
диаметром d=100 мм и длиной l=4 м равен f=20 мм. Определить максимальное
напряжение и углы поворота на опорах, полагая Е=100
ГПа.
Ответ: 
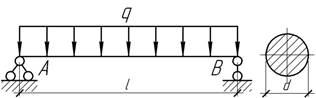
Задача
22.
Для балки жесткостью EIх=200 кНм2
задана эпюра изгибающего момента. Построить эпюры углов поворота и прогибов,
если известно, что прогиб и угол поворота в сечении А
равны нулю, а=1 м, М=3,6 кНм.
Ответ: 
(на расстоянии 1 м от опор А
и В); Vmax=12 мм (посредине балки).
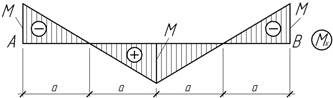
Задача
23.
По заданной эпюре изгибающего момента
определить угол поворота сечения С балки, если прогибы
в сечениях А и В равны нулю, жесткость балки постоянна и равна EIx=200 кНм2, а=1 м, М=2,4 кНм.
Ответ: 
мрад.
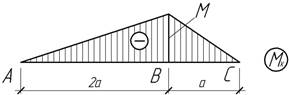
Задача
24.
Определить прогиб и угол поворота на
свободном конце, а также место и величину наибольших перемещений, если М=50 кНм, F=30 кН, EIx=10 МНм2.
Кроме того установить, при каком значении момента М прогиб сечения В равен нулю.
Ответ: VВ=4,5 мм и 
мрад; Vmax=4,7 мм при 
и 
мрад при 
Задача
25.
Для балки АВ постоянной жесткости EIx=1,6 МНм2
установить условия закрепления концов и действующие на нее нагрузки, если
функции прогибов описывается выражением V(ζ)=0,1(ζ4-3ζ3+3ζ2-ζ)
м, где ζ=z/l – относительная координата.
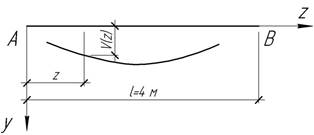
Ответ: Балка шарнирно оперта по концам и
нагружена равномерно распределенной нагрузкой интенсивности q=15 кН/м и опорным моментом МА=60
кНм, направленным против часовой стрелки.
Задача
26.
Подобрать размеры балки квадратного
сечения, найти углы поворота на опорах, прогиб под нагрузкой, а также
наибольший прогиб и его положение по
отношении к левой опоре, если F=4 кН, а=1 м, [σ]=8 МПа, Е=10 ГПа, h/b=1,5.
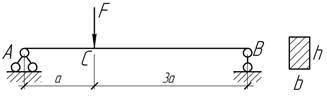
Ответ: b=10 см, 
мрад, 
мрад; Vс=10,7 мм, Vmax=13,2 мм (на расстоянии 1,76 м).
Задача
27.
Стальная балка прямоугольного сечения
5х10 см и длиной l=3 м нагружена по верхней поверхности
равномерно распределенной нагрузкой интенсивности q=50 кН/м. Определить наибольшее
нормальное напряжение, максимальный прогиб и углы поворота на опорах.
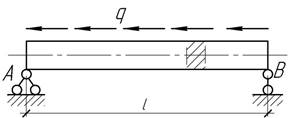
Ответ: 
мм
(в сечении на расстоянии 1,73 м от правой опоры); 
мрад, 
мрад.
Задача
28.
Плоская стальная пружина сечением 15х2 мм
и длиной l=10 см изгибается силой F=40 Н, касаясь при этом круглого цилиндра
радиуса R=1 м. Определить прогиб сечения и
наибольшее нормальное напряжение.
Ответ: VВ=4,6 мм; 
Задача
29.
Какую первоначальную форму следует
принять стальной балке прямоугольного сечения 6х1 см и длиной 2 м, чтобы под
действием силы F=480 Н она полностью соприкасалась
с гладким жестким основанием и давление равномерно распределялось по
длине балке? Чему равно наибольшее нормальное напряжение?
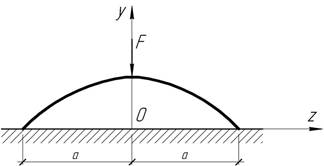
Ответ: У(ζ)=(3-6ζ2+4ζ3-ζ4)
см, 
МПа.
Задача
30.
Упругая балка плотно, но без трения
вставлена в отверстие, высверленное в жестком основании. Интуитивно
представляется, что при нагружении поперечной силой F балка выскользнет из заделки. Но
непонятно, под действием каких сил? Что покажет
динамометр, если силы трения отсутствуют? Выполнить количественную оценку для
стальной балки круглого сечения диаметром d=8,4 мм, полагая F=100 Н и l=100 мм.
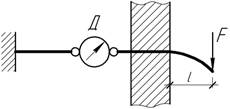
Ответ: Fд=1 Н.
Задача
31.
Стальная балка прямоугольного сечения
6х10 см нагружена на правом конце моментом М=20 кНм.
Подобрать распределенную нагрузку q(z), при действии которой балка остается
прямолинейной, определить наибольшее нормальное и касательное напряжения.
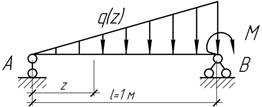
Ответ: 
Задача
32.
Полагая гибкая стальная
пружина прямоугольного сечения 6х1 см и длиной 2 м, изогнутая по дуге
окружности радиуса R=10 м, прижимается двумя силами F к жесткой плоскости. При каких значениях
сил F точки А будут
прижаты к плоскости?
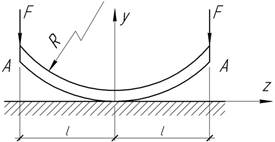
Ответ: F=20 кН.
Задача
33.
Сечения А и В
стальной балки ступенчато-переменного сечения должны быть равноопасными.
Определить из этого условия без учета концентрации напряжений диаметр 
. При найденном значении найти прогиб свободного конца балки, полагая F=10 кН, 
мм.
Ответ: 
мм, Vс=8 мм.
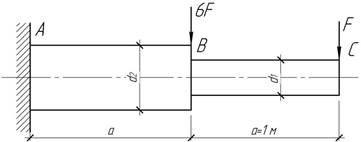
Задача
34.
Определить, при каком отношении моментов
инерции I2/I1 линейное перемещение сечения С равно нулю. Чему равен при этом угол поворота того же
сечения, если EI1=1 МНм2,
М=54 кНм, а=1
м, b=2 м.
Ответ:
I2/I1=4, 
мрад.
Задача
35.
Балка равного сопротивления постоянной
высоты h=2 см меняет ширину прямоугольного
сечения b(z) от нуля на опоре А
до 
на
опоре В по линейному закону. Значение затем сохраняется на всем участке ВС.
Определить величину прогиба сечения С, полагая М=500 Нм, Е=200 ГПа, а=40
см.
Ответ: Vс=20 мм.
Задача
36.
Пренебрегая влиянием концентрации
напряжений, вычислить наибольшие нормальные и касательные напряжения, а также
наибольший прогиб балки, полагая F=5 кН, Е=10 ГПа, 
см,
см, b=3 см, а=20 см.
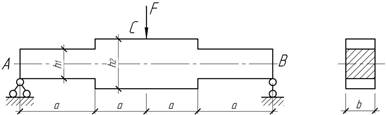
Ответ: 
Vс=0,73 мм.
Задача
37.
Нарисуйте форму упругой линии для следующих балок.
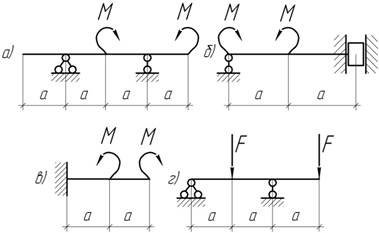
Задача
38.
Как загружена балка, если ее упругая линия образованна дугами окружностей радиуса R?
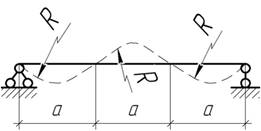
Задача
39.
Сравните форму упругой линии для двух балок.
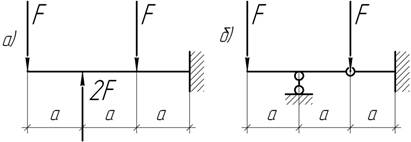
Задача
40.
Выяснить форму упругой линии балки на участке ВС и определите радиус кривизны, если жесткость поперечного сечения равнаEIх.
Задача
41.
Чему равен радиус кривизны балки прямоугольного профиля в среднем сечении С? Дано: Е, q, l, b, h.
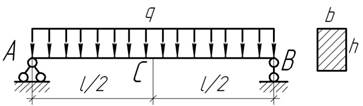
Задача
42.
Какой знак необходимо выбрать в
дифференциальном уравнении упругой линии балки 
для указанных случаев?
Задача
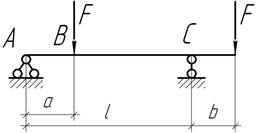
43.
При каком размере а прогиб балки на участке АВ изменяется по линейному закону?
Задача
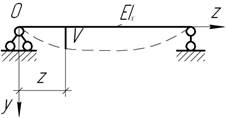
44.
Балка длиной l=2 м, шарнирно опертая по концам,
изгибается согласно уравнению 
. Какая нагрузка вызывает такой изгиб?
Задача
45.
Имеются две балки равной длины и одинакового поперечного сечения, одна из которых составлена из 5 отдельных полос, не связанных между собой. Для какой из балок прогиб будет больше и почему?
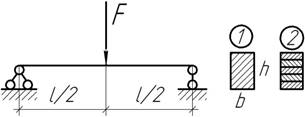
Задача
46.
Чему равен угол поворота на опоре В, если прогиб на свободном конце составляет 10 мм?
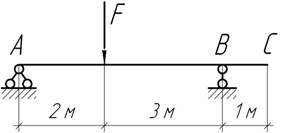
Задача
47.
Чему равны перемещения в середине пролета балок?
Задача
48.
Какую силу F можно приложить в дополнение к погонной нагрузке q=6 кН/м, чтобы наибольшие нормальные напряжения не превышали 160 МПа, а наибольший прогиб не превосходил 1/250 пролета балки l=2 м.
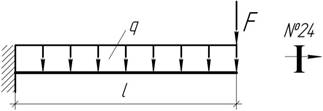
Ответ: F=16,26 кН
Задача
49.
Определить модуль упругости материала балки,
радиус кривизны в сечении А и угол поворота на
свободном конце, если и
прогиб в точке В равен 
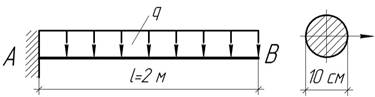
Ответ: Е=70 ГПа, 
Задача
50.
Определить коэффициент К, при котором прогиб сечения D равен нулю. Чему при этом равен прогиб под силой F?
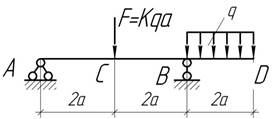
Ответ:
К=11/3, Vс=(26/9)qа4/EIx
Задача
51.
При
действии момента М=100 Нм, касательная и упругой
линии балки на свободном конце составляет угол 
Определить модуль упругости материала балки,
радиус кривизны оси, прогиб в точке В и наибольшее
напряжение изгиба.
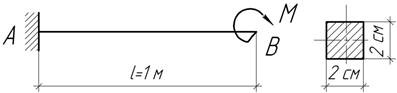
Ответ:
Е=200 ГПа, ρ=26,7 м, 
Задача
52.
Стальная двутавровая балка №20 длиной 4 м нагружена сосредоточенным
моментом, вызывающем наибольшее напряжение изгиба, равные 100 МПа.
Определить величину момента М, радиус окружности, по которой изгибается балка и
прогиб на свободном конце.
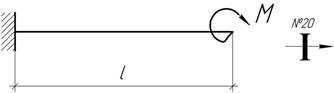
Ответ:
М=18,4 кНм; 
f=4 см.
Задача
53.
Какую силу F надо приложить к свободному концу балки АВ, нагруженным
собственным весом, чтобы суммарное перемещение сечения В
было равно нулю. Погонный вес балки q, изгибная жесткость EI и длина l известны.
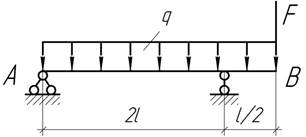
Ответ: F=9ql/16
Задача
54.
При какой длине консоли а угол поворота на опоре В равен нулю? Чему равен в этом случае прогиб на конце консоли?
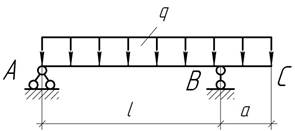
Ответ: 
Задача
55.
Какую силу F нужно приложить посередине пролета АВ в дополнение к погонной нагрузке q=30 кН/м, чтобы прогиб конца равнялся нулю, если l=3 м, а=2 м?
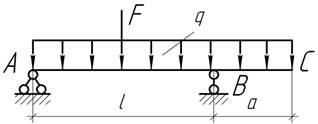
Ответ: F=100 кН
Задача
56.
Стальная полоса длиной l=10 см и толщиной t=2 мм испытывает действие погонной нагрузки q=160 Н/м. Определить ширину полосы в из условия, что максимальный угол поворота равен 10 мрад. При найденном значении в вычислить наибольший прогиб и максимальное напряжение изгиба.
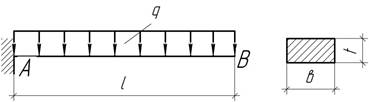
Ответ: в=20 мм, f=0,75 мм,
Задача
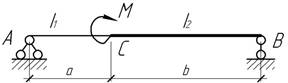
57.
При каком отношении М1/М2 угловое перемещение левого торца балки будет равно нулю?
Задача
58.
Какому положению подвижной нагрузки F соответствует наибольший прогиб сечения С?
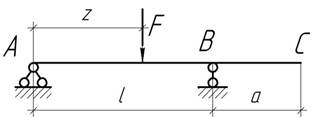
Ответ: z=0,577l
Задача
59.
Найти точку приложения силы F, если отношение углов поворота на опорах 
.
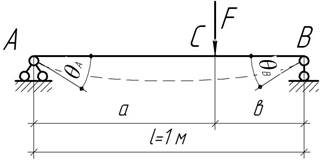
Ответ: а=80 см.
Задача
60.
При каком значении коэффициента β прогибы концов балки будут одинаковы?
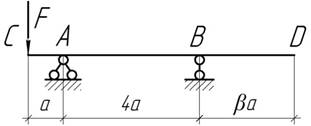
Ответ: β=2,5
Задача
61.
Балка симметричного сечения высотой h=20 см и длиной 2 м изгибается под действием силы F, вызывающей наибольшие напряжения, равные 
Найти прогиб и угол поворота на свободном
конце, пологая Е =100 ГПа.
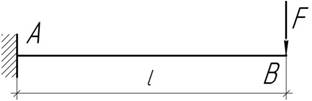
Ответ: 
Задача
62.
При какой нагрузке q стальная балка прямоугольного сечения 6х10 см и длиной 8 м, опирающаяся
на шарнирные опоры высотой 
будет иметь касание на половине ее длины с
абсолютно жестким основанием. Чему равны в этом случае наибольшие нормальные
напряжения?
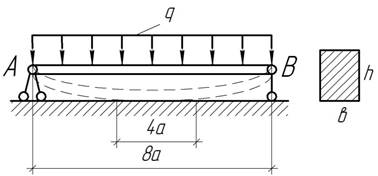
Ответ: q=30кН/м, 
Задача
63.
Наибольший прогиб балки круглого сечения диаметром d=100 мм и длиной l=4 м равен f=20 мм. Определить максимальное напряжение и углы поворота на опорах, пологая Е =100 ГПа.
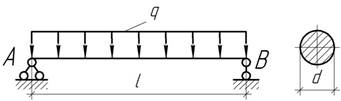
Ответ: 
Задача
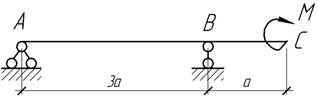
64.
На
каком расстоянии а
от средней опоры нужно приложить момент М, чтобы балка на левом пролете
оставалась прямой? Изгибная жесткость EI балки постоянна.
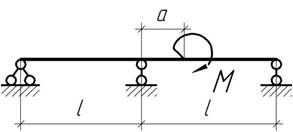
Ответ: а=0,423l
Задача
65.
Шарнирно опертая по концам стальная балка длиной 1 м нагружена моментами М=100 Нм. Найти наибольший прогиб, углы поворота на опорах и горизонтальное смещение подвижной опоры.
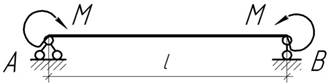
Ответ: f=25 мм, 
Задача
66.
При каком значении коэффициента К прогиб сечения с равен нулю? Чему равен угол поворота этого же сечения?
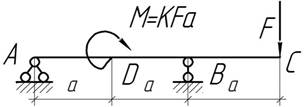
Ответ: К=1,2, 
Задача
67.
Шарнирно опертая по концам балка квадратного
сечения длиной 4 м испытывает действие погонной нагрузки q=8 кН/м. определить максимальный прогиб балки и радиус кривизны
в ее среднем сечении, если наибольшее напряжение изгиба равно 12 МПа и модуль
упругости Е=10 ГПа.
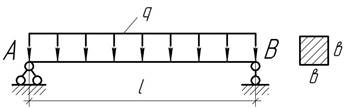
Ответ: f=2 см, ρ=250/3 м
Задача
68.
Длинная труба наружным диаметром d=130 мм и толщиной t=4,9 мм поднимается за середину силой F. Из условия прочности трубы определить максимальную высоту
подъема, длину приподнятой части l и
необходимую величину силы F, если 
.
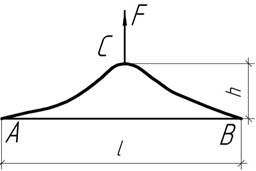
Ответ: 
Задача
69.
По заданной эпюре изгибающего момента
определить угол поворота сечения С балки, если прогибы
в сечениях А и В равны нулю, жесткость балки постоянна и равна EIх=200 кНм2, а=1 м, М=2,4 кНм.
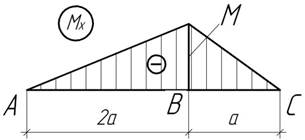
Ответ: 
Задача
70.
Балка пролетом l, защемлена одним концом, несет нагрузку только от собственного веса. Как изменится прогиб и угол поворота на свободном конце, если все размеры балки увеличить в 2 раза?
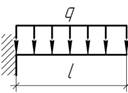
Задача
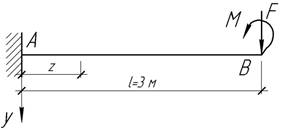
71.
Определить вертикальное перемещение уА точки А консольной балки, изображенной на рисунке.
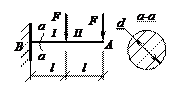
Ответ: yA = 224Fl3/(E𝜋d 4).
Задача
72.
Определить вертикальное перемещение уВ точки В консольной балки, нагруженной сосредоточенным моментом m на конце консоли (см.
рис.). Балка имеет постоянную по длине жесткость на изгиб EIz.
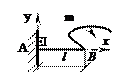
Ответ: yB = ml2/(2EIz).
Задача
73.
1) Определить вертикальное перемещение уВ точки В консольной балки, нагруженной равномерно распределенной нагрузкой q и с постоянной жесткостью на изгиб EIz (рис. 1).
2) Определить вертикальное перемещение уВ и угол поворота φB точки В консольной балки с постоянной жесткостью EI на изгиб (рис. 2).
3) Определить вертикальное перемещение уВ и угол поворота φB точки В однопролетной балки с постоянной жесткостью EI на изгиб (рис. 3).
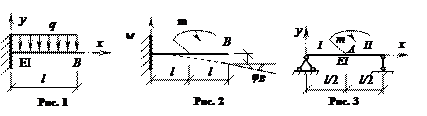
Ответ к рис.1: yB = ql4/(8EIz).
Ответ к рис.2: yB = 3ml2/(2EI); φB =
ml/(EI).
Ответ к рис.3: yB = 0; φB =
ml/(12EI).
Задача
74.
Определить вертикальное перемещение уС и угол поворота φC точки С консольной балки с постоянной жесткостью EIz на изгиб (см. рис.). Определить также уА и φA в точке А.
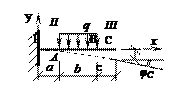
Ответ: φC = q[(a + b)3 – a3]/(6EIz); yC
= q{3(a + b)4 – 3a4 – 4a3b + 4c[(a
+ b)3 –a3]}/(24EIz);
φA = qab(a + b)/(2EIz), yA = qa2b(4a + 3b)/(12EIz).
Задача
75.
Определить максимальный прогиб консольной балки из электросварной прямошовной трубы с наружным диаметром D = 168 мм и толщиной стенки t = 6 мм, заделанной одним концом. Прогиб определить от действия собственного веса трубы. Длина консоли – 5 м. Проверить прочность консольной балки из стали С255, γc= 1.
Ответ: ymax = 0,9 см; σx,max= 24,7 МПа; τmax= 0,8 МПа.
Задача
76.
Балка постоянного сечения АВС
защемлена одним концом и загружена, как указано ниже на схемах. Определить
прогибы и углы поворота в сечениях В и С
методом Мора-Верещагина если: F = 20 кН; М0 =40 кНм; q = 20 кН/м; b =
|
Схема балки |
Ответ: |
|
|
а |
|
φB=-0,00096 φC=-0,00163 yB=-1,88 см yC=-4,3 см |
|
б |
|
φB=0 φC=-0,0083 yB=0 yC=-0,83 см |
|
в |
|
φB=-0,03125 φC=-0,034 yB=-5,6 см yC=-12,3 см |
Задача
77.
Определить прогибы в точках обозначенных буквой А, а также угол поворота сечений, обозначенных буквой В, если Е = 2∙105 МПа.
|
|
Схема балки |
J в см4 |
Ответ: |
|
|
yA в см |
φB |
|||
|
а |
|
1600 |
-1,6 |
-0,0107 |
|
б |
|
4000 |
-1,237 |
-0,00769 |
|
в |
|
2000 |
-0,5 |
+0,00333 |
|
г |
|
2500 |
-0,96 |
+0,0096 |
|
д |
|
3000 |
+1,611 |
+0,0164 |
|
е |
|
3500 |
+0,667 |
-0,0076 |
|
ж |
|
2500 |
-0,333 |
-0,00133 |
|
з |
|
2500 |
+0,5 |
-0,04 |
Определение перемещений в рамах
Задача 1.
Определить горизонтальное смещение хA точки A ломаного бруса, показанного на рисунке. Жесткость на изгиб всех участков ломаного бруса постоянна.
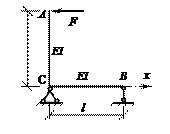
Ответ: хА = 2Fl3/(3EI).
Задача 2.
Определить углы поворота поперечных сечений на опорах ломаного бруса, изображенного на рисунке. Жесткость на изгиб всех участков ломаного бруса постоянна и равна EI.
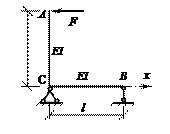
Ответ: 𝜑B= Fl2/(6EI); 𝜑C= Fl2/(3EI).
Задача 3.
Определить вертикальное перемещение поперечного сечения с абсциссой х = l/2 (см. рис.). Жесткость на изгиб всех участков ломаного бруса постоянна и равна EI.
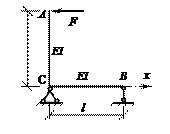
Ответ: y = Fl3/(16 EI) при x = l/2.
Задача 4.
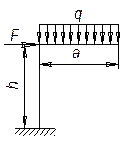
Для приведенных ниже схем а, б, в загружения рамы постоянного сечения из стали (Е = 2∙106 кг/см2) определить величину вертикального перемещения y, горизонтального перемещения ∆ и угла поворота φ свободного конца.
|
|
Схема рамы |
Числовые усилия |
Ответ: |
|
а |
|
F=20 кН M0=10 кН∙м а=2 м h=4 м J= 104
см4 |
|
|
б |
|
F=20 кН q=1 кН/м а=1 м h=4 м J= 8000
см4 |
|
|
в |
|
F=20 кН q=1 кН/м а=1 м h=3 м J= 4000
см4 |
|
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
