Главная

Лекция 5. Оболочки

5.1 Общие сведения об оболочках

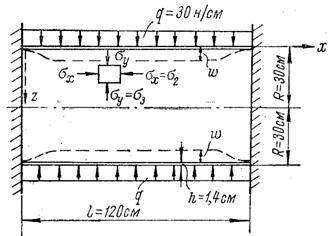
Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина h) мало по сравнению с другими размерами тела. Оболочки принадлежат к сплошным непрерывным системам (к дискретным системам относятся, например, стержневые системы). В настоящей главе рассматриваются наиболее часто применяемые в машиностроении оболочки постоянной толщины.

Оболочки широко применяются в различных отраслях техники. Например, подкрепленной замкнутой оболочкой является прочный корпус подводной лодки. Корпус парогенератора или турбины энергетической установки также рассчитывают как оболочку.

Цистерны, воздушные и газовые баллоны обычно представляют собой оболочки вращения цилиндрической, шаровой или каплевидной формы. Как оболочки рассматриваются и строительные конструкции - перекрытия и купола всевозможных очертаний со значительными пролетами, а также самолетные конструкции (фюзеляж, крылья и оперение).

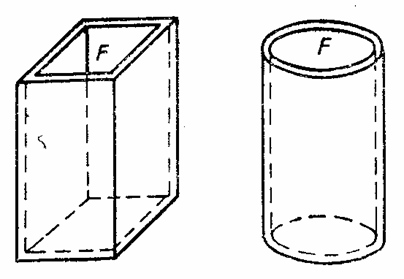
Большое распространение оболочек объясняется их экономичностью по сравнению с равнопрочными конструкциями, состоящими из плоских пластин. Например, при одной и той же площади F поперечного сечения сосуда и одинаковом постоянном внутреннем давлении наибольшие напряжения в стенке сосуда вдали от торцов при прямоугольной призматической форме (рис. 78,а) будут в несколько десятков раз больше, чем при цилиндрической форме (рис. 78, б). Это обусловлено тем, что в пластинах, образующих прямоугольный сосуд, вследствие изгиба наблюдается большая неравномерность распределения напряжении, чем в цилиндрической оболочке.

а	б

Рис. 78

Срединной поверхностью оболочки называется геометрическое место точек, равноудаленных от ее наружной и внутренней поверхностей. Считается, что кромка незамкнутой оболочки образована поверхностью, нормальной к срединной поверхности.

Условно, в зависимости от отношения толщины h оболочки к наименьшему радиусу R кривизны ее срединной поверхности, различают два класса оболочек: толстые оболочки, у которых , и тонкие оболочки, у которых. В уравнениях, относящихся к тонкой оболочке, наибольшим значением можно пренебречь по сравнению с единицей, не превышая обычную для технических расчетов погрешность в 5 % :

Большая часть оболочек, применяемых в машиностроении, относится к тонким оболочкам, однако основана на использовании достаточно сложного математического аппарата. Их теория построена в предположении, что материал изотропен, обладает идеальной упругостью, подчиняется закону Гука и перемещения точек оболочки малы по сравнению с ее толщиной. Кроме того, используются два допущения теории пластин: 1) о прямых нормалях, т. е. считается, что линейные элементы оболочки, нормальные к срединной поверхности, остаются прямолинейными и нормальными к изогнутой срединной поверхности; 2) об отсутствии поперечного давления, т. е. предполагается, что нормальные напряжения, перпендикулярные к срединной поверхности, пренебрежимо малы.

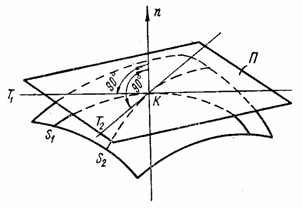
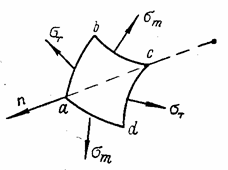
Напомним некоторые сведения из теории поверхностей. В любой точке К криволинейной поверхности (рис. 79,а) имеется плоскость П, касательная к поверхности, в которой лежат все касательные Т к плоским кривым S, проведенным на поверхности. Нормаль n в точке К перпендикулярна к касательной плоскости.

а	б

Рис. 79

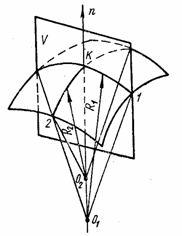
Нормальное сечение поверхности в точке К получается, если рассечь ее плоскостью V, содержащей нормаль п (рис. 79,б). В любой точке К можно провести на поверхности две взаимно перпендикулярные линии главной кривизны, из которых одна имеет наибольший радиус кривизны R₁, а другая наименьший R₂ по отношению к радиусам всех линий, проходящих через точку К.

Величины и , обратные этим радиусам, называются главными кривизнами. Центры кривизны О₁ и O₂ в общем случае не совпадают.

5.2 Понятие о расчете оболочки произвольной формы

При изучении оболочек произвольной формы в общем случае пользуются системой криволинейных координат. Для оболочек вращения применяют цилиндрическую или сферическую системы.

При цилиндрической системе (рис. 80) за координаты принимаются: расстояние z по вертикали, отсчитываемое от точки О, определяющее параллель П, и угол , отсчитываемый от начальной плоскости у0z, определяющий положение плоскости BOA, в которой лежит меридиан М. Пересечение параллели П и меридиана М определяет положение точки К на поверхности. Радиус R представляет собой функцию от z.

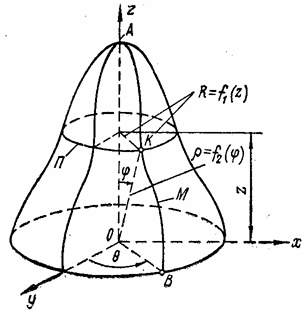
Рис. 80

При сферической системе за координаты принимаются: угол , отсчитываемый в плоскости BOA от вертикальной оси z, определяющий положение параллели П, и угол , определяющий положение меридиана М. Радиус представляет собой функцию от .

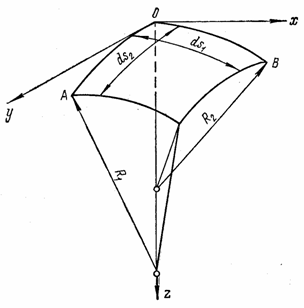
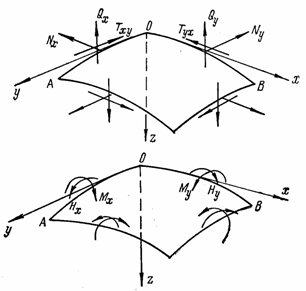
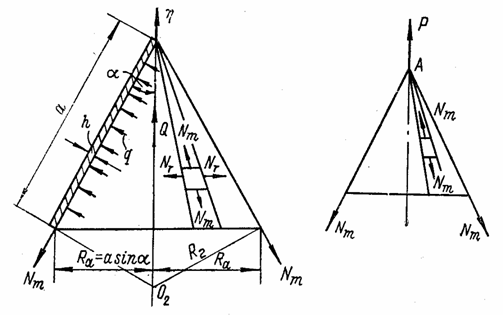
Выделим из оболочки, нагруженной непрерывно распределенной нагрузкой, элемент АОВ (рис. 81,а) двумя парами смежных взаимно ортогональных сечений, содержащих главные кривизны оболочки. Обозначим через R₁ и R₂ соответствующие радиусы главных кривизн. Взаимно перпендикулярные оси х и у направим по касательным в точке О к линиям главных кривизн, а ось z - по нормали к срединной поверхности в точке О. На элемент АОВ действуют десять погонных усилий (рис. 81,б): изгибающие моменты М_х и M_y,

а	б

Рис. 81

крутящие моменты Н_х и Н_у, продольные силы N_x и N_y, поперечные силы Q_х и Q_y и сдвигающие силы Т_xу и Т_уx. Так как элемент выделяется взаимно ортогональными плоскостями, нормальными к срединной поверхности, в пересечении плоскостей с оболочкой образуются фигуры, имеющие разные длины волокон в зависимости от длины радиусов R₁ и R₂. Размер волокна длиной, равной единице (рис. 82), на расстоянии z от срединной поверхности с

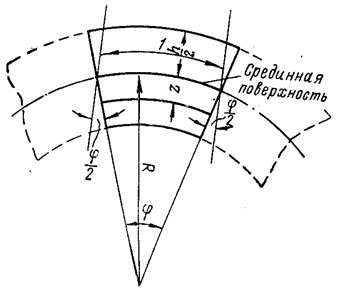
Рис. 82

радиусом R после деформации окажется

Поэтому для погонных усилий, действующих по граням выделенного элемента АОВ (см. рис. 81,б и 82), можно составить такие выражения:

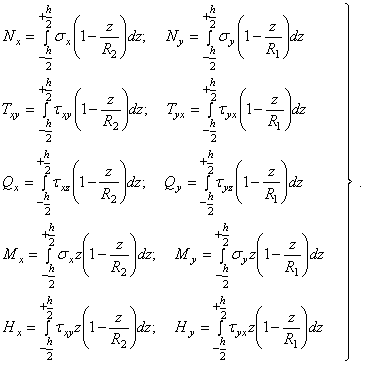(5.1)

При переходе от одной грани выделенного элемента к соседней, расположенной на расстоянии dS₁ или dS₂ (рис. 81,а) от первой, необходимо учитывать приращение усилий.

Вследствие того, что трапеции, образующие боковые грани элемента, различны, сдвигающие силы Т_xу и Т_уx не равны между собой, несмотря на справедливость закона парности касательных напряжений. Однако обычно толщина h, а, следовательно, и расстояние z малы по сравнению с радиусами R₁ и R₂, поэтому отношения и малы по сравнению с единицей и могут быть сразу отброшены. Тогда

,

т. е. закон парности сдвигающих усилий становится действительным.

Для решения статически неопределимой задачи о напряженном состоянии можно составить следующие уравнения:

1. Пять дифференциальных уравнений равновесия, представляющих собой суммы проекций всех сил, действующих на элемент, на оси Ох, Оу и Оz и суммы моментов этих сил относительно осей Ох и Оу. Уравнение равновесия в виде суммы моментов всех сил относительно оси Оz превращается в тождество 0 = 0 на основании закона парности касательных напряжений.

2. Три геометрических дифференциальных уравнения, связывающих относительные деформации , и с составляющими перемещениями u₀, v₀ и w₀ срединной поверхности, и три геометрических дифференциальных уравнения, связывающих величины k_x и k_y, характеризующие изменения кривизн срединной поверхности, и величину , характеризующую ее кручение, с составляющими u₀, v₀ и w₀. Появление перемещений k_x, k_y и связано с тем, что элемент оболочки под нагрузкой получает дополнительное искривление.

3. Шесть уравнений, аналогичных закону Гука для пластины, связывающих между собой соответствующие усилия с составляющими деформациями.

Таким образом, для нахождения восьми усилий М_х, M_y, Q_x, Q_y, H_x = Н_у, N_x, N_y, Т_xу = Т_уx, шести составляющих перемещений u₀, v₀, w₀, k_x, k_y и и трех относительных деформаций , и , т. е. семнадцати неизвестных, имеем 5 + + 3 + 3 + 6 = 17 уравнений.

Число граничных условий для каждой кромки вырезанного элемента равно четырем. Они могут быть геометрическими (равенство нулю перемещений и, v и w), статическими (равенство нулю погонных усилий М, Q, N и Т) или смешанными. Например, для свободно опертой кромки (= const, рис. 83) можно написать смешанные условия: и = 0, w = 0, М_x = 0, N_x = 0. Общее число условий равно числу произвольных постоянных, получающихся при интегрировании дифференциальных уравнений.

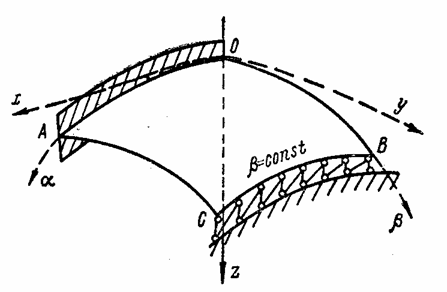
Рис. 83

Решение системы семнадцати уравнений при заданных граничных условиях в общем виде в ряде случаев не может быть получено. Поэтому пользуются обычно решениями для частных случаев формы оболочки и ее нагружения, дающих возможность упростить общие уравнения.

Одно из простых решений получается в тех случаях, когда напряжениями изгиба можно пренебречь, учитывая лишь напряжения, связанные с деформацией срединной поверхности. Соответствующая теория называется безмоментной или мембранной. Она применима в тех случаях, когда радиусы срединной поверхности изменяются плавно, оболочка не имеет переломов и резких изменений толщины. Нагрузка, действующая на оболочку, тоже должна изменяться плавно или быть постоянной.

По безмоментной теории предполагается, что изгибающие и крутящие моменты, а также поперечные силы отсутствуют, т. е.

M_x = M_y = H = Q_x = Q_y = 0,

и остаются лишь продольные силы N_x и N_y и сдвигающие силы Т_xy = Т_yx.

В случае, если оболочка представляет собой оболочку вращения и нагрузка симметрична относительно оси вращения и нормальна к срединной поверхности оболочки, сдвигающие силы Т_xу = Т_ух также отсутствуют и остаются только продольные силы; меридиональные N_m и окружные N_T.

При постоянной интенсивности давления q и постоянных радиусах R₁ и R₂ главных кривизн меридиональные, так же как и окружные погонные силы N_m и N_T, одинаковы во всех точках и напряженное состояние оболочки однородное.

5.3 Оболочка вращения, нагруженная нормальным давлением

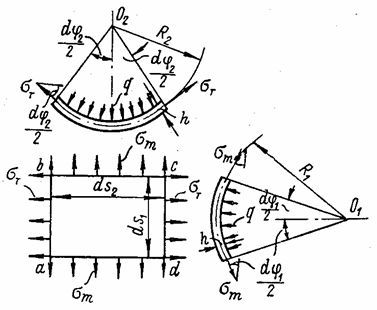
На рис. 84 показана оболочка вращения с постоянной толщиной, нагруженная нормальным давлением интенсивностью q. Вырежем из нее двумя меридиональными сечениями 1 и 2 и двумя экваториальными сечениями 3 и 4 малый элемент abcd, имеющий размеры ds₁ и ds₂. Радиусы кривизны R₁ и R₃

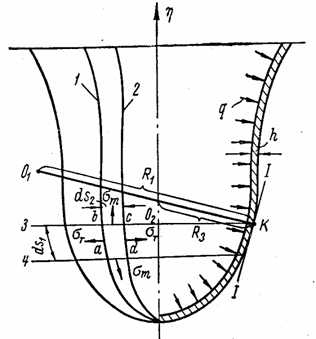
Рис. 84

кривых 1 и 3 в какой-либо точке К оболочки совпадают, так как оба радиуса направлены по нормали к касательной плоскости I – I в этой точке. Центр кривизны 0₁ меридиональной кривой может лежать как внутри очертания оболочки, так и вне оболочки в зависимости от того, выпуклая она или вогнутая, и в зависимости от величины радиуса кривизны R₁, а центр кривизны 0₂ лежит на оси вращения . Геометрическое место радиусов R₃ представляет собой коническую поверхность с вершиной, расположенной на оси .

Составим условия равновесия элемента abcd в виде суммы проекций всех сил, действующих на элемент, на нормаль п к оболочке, проведенную в центре элемента (рис. 85,а). Так как по четырем граням, которыми выделен элемент, в силу симметрии оболочки и нагрузки относительно оси вращения касательные напряжения отсутствуют, эти грани представляют собой главные площадки, а нормальные напряжения - главные напряжения: меридиональное и окружное .

а	б

Рис. 85

На рис. 85,б показаны три проекции элемента abсd и напряжения, действующие по его граням. Сумма проекций усилий, приложенных к элементу, на нормаль

Принимая и учитывая, что

,

получаем

или, после сокращения на произведение ds₁ds₂ и переноса давления q и толщины h в правую часть,

. (5.2)

Так как погонные усилия, действующие в экваториальном и меридианном сечениях,

,

можно получить уравнение (5.2), записанное через погонные усилия,

. (5.3)

Уравнение (5.2) или его разновидность (5.3) называется уравнением Лапласа.

При выводе формул Лапласа внутреннее давление q считалось положительным. Наружное давление q следует подставлять в формулы (5.2) и (5.3) со знаком минус. Радиусы кривизны R₁ и R₂ считаются положительными для выпуклого сосуда и отрицательными для вогнутого. При пользовании указанными правилами знаков положительное усилие или напряжение соответствует растяжению, а отрицательное - сжатию.

Уравнение Лапласа содержит два неизвестных - меридиональные и окружные напряжения (или усилия). Для их определения необходимо дополнительное уравнение, которое получается при отсечении от оболочки части ее и составлении условия равновесия для оставшейся части. Рассекающая плоскость Р - Р обычно выбирается нормальной к оси вращения , но стенка оболочки пересекается по нормали к меридиану (рис. 86). Отбрасывать удобно ту часть, на которой находятся опорные связи, - верхнюю на рис. 86,а и нижнюю на рис. 86,б и в.

а

б в

Рис. 86

Уравнение равновесия оставшейся части подвешенного сосуда, показанной на рис. 86,а сплошной линией, составляем в виде суммы проекции на ось вращения всех сил, действующих на эту часть:

,

откуда

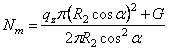. (5.4)

В случае опертой оболочки, показанной на рис. 86,б и в, второй член G числителя формулы (5.4) будет отрицательным. В формуле (5.4) приняты обозначения: q_z - гидростатическое или газовое давление на уровне Р - Р (в случае гидростатического давления q_z = g (Н - z), где - объемный вес жидкости); G - вес жидкости в оставшейся части сосуда; - угол между касательной к меридиональному сечению на уровне Р - Р и осью вращения.

Первый член в числителе формулы (5.4) выражает вес цилиндра, имеющего радиус основания R₂ cos и высоту (H – z). Поэтому в случае опертой оболочки числитель формулы (5.4) представляет собой разность весов цилиндра с основанием, равным площади сечения Р - Р, и части сосуда, расположенной выше этого сечения. Эта разность пропорциональна разности объемов, показанных на рис. 86,б и в штриховкой. Если разность положительна, усилие N_m растягивающее (объем цилиндра больше объема сосуда - рис. 86,б), если разность отрицательна, усилие N_m сжимающее (объем цилиндра меньше объема сосуда - рис. 86,в).

Рассмотрим применение этих уравнении в частных случаях.

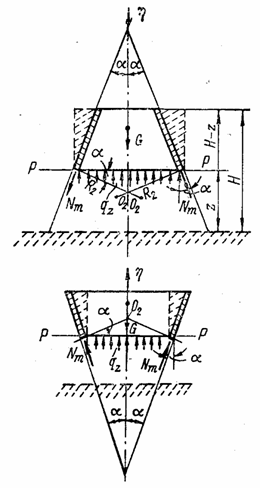
1. Шаровая оболочка с радиусом R, нагруженная радиальной равномерно распределенной нагрузкой (рис. 87).

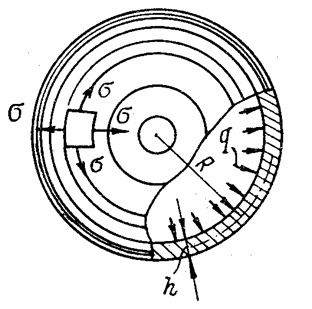
Рис. 87

В этом случае в силу шаровой симметрии

(5.5)

и напряжение s в любой точке и по любому нормальному сечению может быть найдено без помощи дополнительного уравнения. Подстановка значений (5.5) в уравнение (5.2) дает

.

Относительная окружная и равная ей относительная меридиональная деформации по закону Гука

. (5.6)

С другой стороны, относительная окружная деформация

. (5.7)

Приравняв друг другу выражения (5.6) и (5.7), найдем радиальное перемещение

или, заменив s его выражением (5.6), получим:

.

2. Цилиндрическая оболочка с радиусом R, нагруженная нормальной к поверхности равномерно распределенной нагрузкой q (рис. 88).

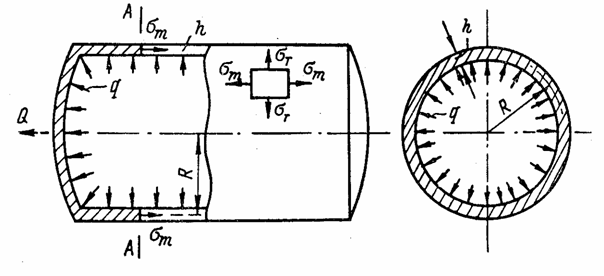
Рис. 88

В этом случае главные радиусы кривизны

и R₂ = R.

Поэтому на основании формулы (5.2) окружное (экваториальное) напряжение

,

где D - диаметр цилиндра.

Второе главное напряжение - меридиональное напряжение - находится из условия равновесия части оболочки слева от сечения А - А. Равнодействующая Q давления на торец уравновешивается усилиями, направленными вдоль образующей, действующими по кольцу, получающемуся при рассечении цилиндра плоскостью А - А. Тогда

,

откуда

.

При отсутствии торцовых днищ в коротком цилиндре = 0, а в длинном .

Относительная окружная деформация для цилиндрической оболочки вычисляется так же, как и для шаровой [см. формулу (5.7)]. Такую же величину имеет и относительная радиальная деформация :

, (5.8)

но по закону Гука

. (5.9)

Приравняв выражения (5.8) и (5.9), найдем радиальное перемещение

или, заменив и их выражениями,

. (5.10)

При отсутствии торцовых днищ в короткой оболочке напряженное состояние можно считать линейным и перемещения вычислять по формуле

. (5.11)

Сравнение формул (5.10) и (5.11) показывает, что при плоском напряженном состоянии радиальное перемещение оболочки меньше, чем при линейном; для стальной оболочки коэффициент уменьшения

,

т. е. перемещения при плоском состоянии составляют 85% от перемещений, вычисленных в предположении линейного состояния.

3. Коническая оболочка с углом при вершине, нагруженная нормальной к поверхности равномерно распределенной нагрузкой q (рис. 89,а).

а	б

Рис. 89

В этом случае главные радиусы кривизны

и из уравнения (5.3) находим

.

Из уравнения равновесия

,

где Q - равнодействующая проекции на ось нормальных давлений на оболочку.

Так как при длине образующей а боковая поверхность оболочки

равнодействующая

.

Меридиональное усилие

. (5.12)

Если в это выражение подставить найденное значение Q, то

.

и

.

4. Выражение для меридионального усилия N_m справедливо также в случае сосредоточенной силы Р, приложенной к вершине А конической оболочки по ее оси (рис. 89,б). В формуле (5.12) равнодействующую Q нужно в этом случае заменить на Р. Так как при этом распределенное давление q равно нулю, из уравнения Лапласа (5.3) следует, что окружное усилие N_T и окружное напряжение равны нулю.

Две главные площадки оболочки вращения совпадают с экваториальным и меридиональным сечениями. Третья главная площадка нормальна к первым двум и параллельна срединной поверхности. При действии на оболочку внутреннего нормального давления элемент 1, выделенный у ее наружной поверхности (рис. 90), находится в плоском напряженном состоянии, а у внутренней поверхности (элемент 2) - в объемном. Третья главная площадка испытывает главное напряжение - q, однако меридиональное и экваториальное напряжения, имеющие, как видно из уравнения Лапласа, порядок , значительно больше (в раз), чем q. Поэтому обычно третьим главным напряжением q пренебрегают и считают, что материал оболочки по всей толщине стенки находится в плоском напряженном состоянии.

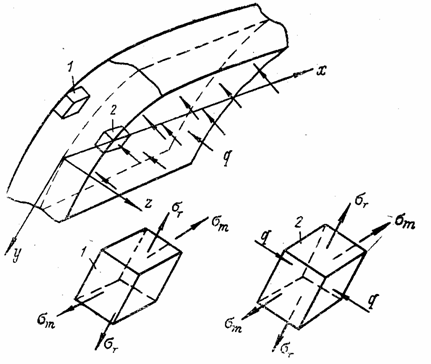
Рис. 90

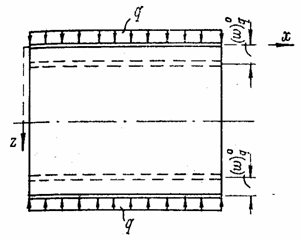
5.4 Изгиб цилиндрической круговой оболочки

Основные зависимости для случая изгиба замкнутой круговой цилиндрической оболочки, нагруженной равномерным радиальным давлением q (рис. 91), можно получить без использования общей теории оболочек. Считаем, что отношением толщины оболочки к радиусу кривизны можно пренебречь ввиду его малости по сравнению с единицей. В таком случае при изгибе деформации и напряжения пропорциональны расстоянию z от волокна до срединной поверхности, а при отсутствии изгиба распределяются равномерно по толщине оболочки.

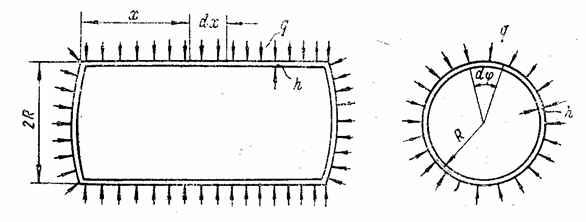
Рис. 91

Выделим из оболочки элемент двумя поперечными сечениями, находящимися на расстоянии dx друг от друга, и двумя радиальными сечениями, образующими между собой угол . Усилия, действующие на вырезанный элемент, показаны на рис. 92.

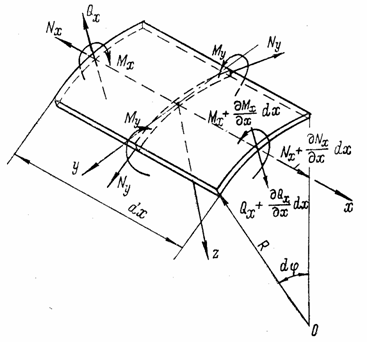
Рис. 92

Вследствие круговой симметрии оболочки и нагрузки относительно оси цилиндра поперечная силы Q_y и крутящие моменты Н отсутствуют, а продольная сила N_y и изгибающий момент M_y постоянны по длине окружности. Вследствие того, что давление q нормально к срединной поверхности, сдвигающие силы Т отсутствуют. Поэтому для десяти составляющих усилий (5. 1) имеем:

.

Остаются лишь усилия, указанные на рис. 92, причем усилия N_у и M_y при переходе от одного радиального сечения к другому не получают приращения. Из шести уравнений равновесия три превращаются в тождества. Остальные три запишутся так:

(5.13)

(5.14)

(5.15)

На основании уравнения (5.13) можно заключить, что т. е. продольная сила N_x постоянна. В частности, она может равняться нулю при отсутствии у цилиндрической оболочки торцовых днищ.

Уравнение (5.14) после замены , сокращения двойки в первом члене и всех членов на примет вид

. (5.16)

В уравнении (5.15) второй член высшего порядка малости может быть отброшен. Тогда после сокращения на оно примет вид:

. (5.17)

Это уравнение показывает, что установленная для стержней зависимость между поперечной силой и изгибающим моментом справедлива и в отношении к рассматриваемой оболочке. Подставив эту зависимость в формулу (5.16) и перейдя от частных производных к полным дифференциалам, ввиду того, что осталась единственная переменная х, получим

. (5.18)

Уравнение (5.18) содержит два неизвестных: N_y и М_x, поэтому для их нахождения необходимо еще одно уравнение, которое составляется исходя из известной величины продольной силы

. (5.19)

От дифференциального уравнения (5.18) в усилиях перейдем к дифференциальному уравнению в радиальных перемещениях w. Для этого усилия выразим через деформации, а деформации - через перемещения.

На основании закона Гука (1.20) при = 0

(5.20)

. (5.21)

Приравняв правые части уравнений, найдем:

. (5.22)

Относительная окружная деформация

. (5.23)

Подставив значения из формулы (5.23) в (5.21), на основании формулы (5.24) получим выражение для продольной силы

,

а после раскрытия скобок

. (5.25)

Изгибающие моменты, выраженные через перемещения w, определим с учетом дополнительного момента (М_х)_Nx = Nw, который дает продольная сила:

.

Так как при равномерном радиальном сжатии поперечное сечение цилиндра остается круговым, радиальное перемещение w одинаково во всех точках окружности и кривизна изогнутой срединной поверхности в экваториальном направлении от изгиба

Поэтому изгибающие моменты от поперечной нагрузки q

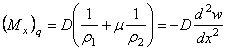, (5.26)

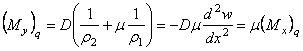, (5.27)

а изгибающий момент

. (5.28)

Подставим найденные значения (5.25) и (5.28) в уравнение (5.18):

.

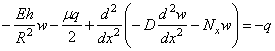Группируя члены, меняя знаки, учитывая выражение (5.19) и считая, что D - постоянная величина, получаем дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях

. (5.29)

Продольная сила N_x влияет на величину перемещения w незначительно, поэтому, пренебрегая ею, вместо формулы (5.23) на основании (5.26) имеем

;

вместо формулы (5.25)

, (5.30)

и вместо формулы (5.28)

. (5.31)

Тогда приближенное дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях

. (5.32)

В уравнении (5.31) введено обозначение

.

Величина

называется коэффициентом затухания перемещений. Она показывает, насколько затухают перемещения по мере удаления от места приложения усилия.

Расчет цилиндрической оболочки, как точный с помощью формулы (5.29), так и приближенный с помощью формулы (5.32), дает близкие результаты. Поэтому в дальнейшем будем пользоваться уравнением (5.32). Если проинтегрировать его и получить приближенное уравнение изогнутой срединной поверхности оболочки w = f (x) (без учета влияния продольной силы N_х), то все усилия и перемещения, характеризующие напряженно деформированное состояние оболочки, получатся по формуле (5.19), (5.30), (5.31) (5.27) и (5.17).

Угол наклона касательной к изогнутой срединной поверхности

.

Следует иметь в виду, что знаки в перечисленных формулах предусматривают внешнее радиальное давление q. При внутреннем давлении знаки должны быть изменены на обратные.

Интеграл дифференциального уравнения (5.32) складывается из интеграла однородного уравнения и частного решения уравнения (5.32); он может быть представлен с помощью показательных функций в виде

. (5.33)

или, если заменить показательные функции гиперболическими на основании зависимостей

,

в виде

. (5.34)

В выражениях (5.33) и (5.34) f(х) - частное решение дифференциального уравнения (5.32). В случае радиальной нагрузки интенсивностью q, равномерно распределенной по поверхности оболочки, частное решение f(х), имеет вид

. (5.35)

При этом

,

и уравнение (5.32) при подстановке в него решения (5.35) превращается в тождество.

Коэффициенты С₁, . . ., С₄ и А₁, . . ., А₄ представляют собой произвольные постоянные, определяемые из граничных условий. Если усилия и перемещения на одном конце цилиндрической оболочки не влияют на усилия и перемещения, возникающие на другом конце, оболочка считается длинной. Если эти факторы влияют друг на друга, то оболочка считается короткой.

Если в дифференциальном уравнении (5.32) принять правую часть равной нулю (при отсутствии радиальной нагрузки q), то оно примет вид

. (5.36)

Уравнение (5.36) представляет собой уравнение балки на упругом основании, в нем принято обозначение

, (5.37)

где k - коэффициент постели, связывающий интенсивность реакции основания q с прогибом балки w:

q = -kw.

Вследствие аналогии между уравнениями (5.32) и (5.36) полоску шириной, равной единице, вырезанную из цилиндрического сосуда вдоль образующей, можно рассматривать как балку на упругом основании и использовать все решения, применяемые при расчете такой балки, для расчета цилиндрической оболочки. При этом реакция основания

,

что следует из рис. 93.

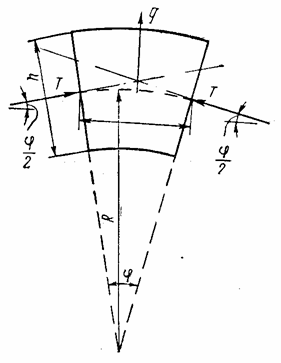
Рис. 93

Для полоски шириной, равной единице, центральный угол дуги , а сжимающие силы .

Поэтому

.

Следовательно,

и коэффициент (5.37), если заменить в его выражении жесткость балки EJ цилиндрической жесткостью D,

представляет собой коэффициент затухания перемещений.

5.5 Определение усилий и перемещений в длинной цилиндрической оболочке

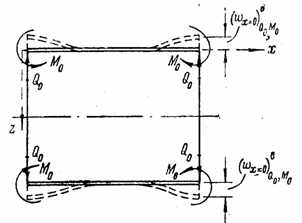
Расчетный случай 1. Длинная оболочка с круглым поперечным сечением нагружена погонными изгибающими моментами M₀ и погонными поперечными силами Q₀ по торцу при х = 0 (рис. 94).

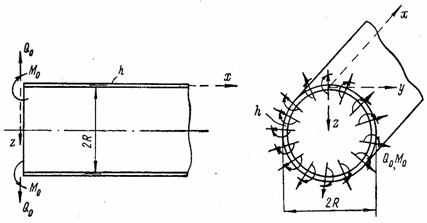
Рис. 94

Интенсивность радиальной нагрузки равна нулю, и поэтому дифференциальное уравнение (5.32) будет однородным:

Интеграл его не содержит частного решения и имеет вид

(5.38)

Усилия M₀ и Q₀ вызывают местный изгиб, радиальные перемещения быстро затухают и одно из условий для определения произвольных постоянных C₁, . . ., С₄ можно записать так: 1) при . Еще два условия можно записать для нагруженного торца: 2) при х = 0 М_x = М₀ 3) при х = 0 Q_x = Q₀ . Четвертого условия, как увидим, не понадобится.

Действительно, при

поэтому на основании первого условия получим

(5.39)

Чтобы это условие соблюдалось, круглая скобка должна быть равна нулю. Синус и косинус одновременно быть равными нулю не могут, следовательно, условие (5.39) возможно, только если С₁ = С₂ = 0. Тогда уравнение (5.38) принимает вид

(5.40)

и для определения двух постоянных С₃ и С₄ достаточно двух условий: второго и третьего. Из второго условия найдем [см. формулу (5.26)]

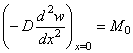(5.41)

и на основании формулы (5.17)

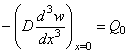. (5.42)

Вычислим производные по х от выражения (5.40) для перемещения w:

(5.43)

(5.44)

(5.45)

Произвольную постоянную C₃ найдем, подставив выражение (5.44) в условие (5.41). Учитывая, что синус нуля равен нулю, косинус - единице, а е⁰ = 1, получим

откуда

. (5.46)

Подставив это выражение С₃ в выражение (5.45), найдем из уcловия (5.42)

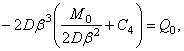
откуда

. (5.47)

Подстановка значений (5.46) и (5.47) в формулу (5.40) дает уравнение изогнутой срединной поверхности оболочки

. (5.48)

Подставив выражения (5.46) и (5.47) в формулы (5.43), (5.44) и (5.45), получим

(5.49)

(5.50)

(5.51)

Введем для комбинаций показательной и тригонометрической функций , входящих в уравнения (5.48) - (5.41), следующие обозначения:

. (5.52)

Тогда радиальное перемещение

, (5.53)

а его производные

Имея выражения для перемещения w и его производных, можно, пользуясь соответствующими формулами, получить все усилия и перемещения в оболочке, в частности:

- угол наклона касательной к оси х

(5.54)

- изгибающий момент в меридиональном сечении

(5.55)

- поперечную силу в меридиональном сечении

. (5.56)

Для входящих в эти формулы функций (5.22) составлена табл. 4, дающая численные значения безразмерных величин в зависимости от . При > 0 все четыре функции по абсолютной величине меньше единицы. По мере возрастания х эти функции затухают, что подтверждает местный характер усилий и перемещений. При = 0 (а значит, и при х = 0), функции равны единице, а функция равна нулю. Поэтому на торце цилиндрической оболочки:

Таблица 4

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,5 2,0 2,5 3,0 4,0 5,0	+ 1,0000 + 0,9907 + 0,9651 + 0,9267 + 0,8784 + 0,8431 + 0,7628 + 0,6997 + 0,6354 + 0,5712 + 0,5083 + 0,2384 + 0,0667 - 0,0166 - 0,04226 - 0,02583 - 0,00455	+ 1,0000 + 0,8100 + 0,6398 + 0,4888 + 0,3564 + 0,2415 + 0,1431 + 0,0599 - 0,0093 - 0,0657 - 0,1108 - 0,2068 - 0,1794 - 0,1149 - 0,05632 + 0,00189 + 0,00837	+ 1,0000 + 0,9003 + 0,8024 + 0,7077 + 0,6174 + 0,5323 + 0,4530 + 0,3708 + 0,3131 + 0,2527 + 0,1988 + 0,0158 - 0,0563 - 0,0658 - 0,04929 - 0,01197 + 0,00191	+ 0,0000 + 0,0903 + 0,1627 + 0,2189 + 0,2610 + 0,2908 + 0,3099 + 0,3199 + 0,3223 + 0,3185 + 0,3096 + 0,2226 + 0,1231 + 0,0491 + 0,00703 - 0,01386 - 0,00646

- радиальное перемещение по формуле (5.53)

, (5.57)

где знак минус показывает, что при принятых за положительные усилия М₀ и Q₀ (см. рис. 94) и оси z, направленной по радиусу к центру кривизны, перемещение w происходит от центра (радиус R увеличивается);

- угол наклона касательной по формуле (5.54)

; (5.58)

- изгибающий момент М_х и поперечная сила Q_x при х = О по формулам (5.55) и (5.56) получаются равными заданным на кромке величинам М₀ и Q₀.

Расчетный случай 2. Оболочка нагружена радиальными погонными усилиями Р, распределенными по окружности в сечении х = 0 (рис. 95). Начало координат выбираем в сечении, в котором приложена радиальная нагрузка. Для каждой половины оболочки слева и справа от начала координат можно применить решение, полученное для расчетного случая 1.

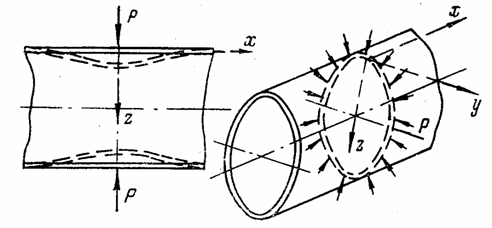
Рис. 95

Граничные условия для определения произвольных постоянных следующие: 1) х = 0, (касательная в месте приложения силы, вследствие симметрии изгиба оболочки, горизонтальна); 2) х = 0, (погонная поперечная сила Q₀ в начале координат равна половине радиальной нагрузки). Положительные направления изгибающего момента и поперечной силы показаны на рис. 94.

Пользуясь первым условием и формулой (5.58), находим

откуда

или, учитывая второе условие,

. (5.59)

Подставив значения Q₀ из второго условия и М₀ из формулы (5.59) в формулу (5.53), получим уравнение радиальных перемещений

, (5.60)

так как

.

Продифференцировав выражение (5.60), определим в функции угол наклона касательной , изгибающий момент М_x и поперечную сил Q_x

(5.61)

(5.62)

(5.63)

Так как функции имеют наибольшее значение, равное единице при и х равных нулю, а функция при этом равна нулю, то

Эпюры w, M_x и Q_x показаны на рис. 96.

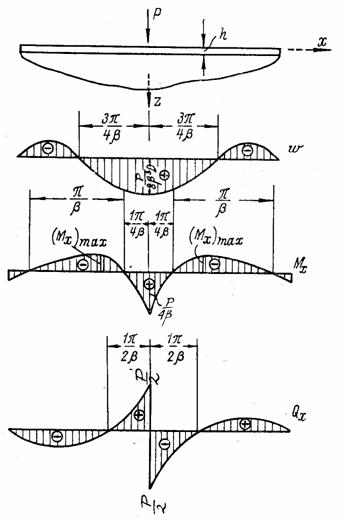
Рис. 96

Видно, что ординаты эпюр быстро убывают по мере удаления от сечения х = 0, в котором приложена радиальная нагрузка. При можно считать, что усилия и деформации пренебрежимо малы. Поэтому при длине оболочки можно полагать, что усилия и перемещения на одном конце не влияют на эти факторы на другом конце. Такие оболочки относятся к длинным оболочкам.

Чтобы оценить величину l, подсчитаем ее при таких данных:

R = 0,5 м; h = 1 см; E = 2 Мн/м²; = 0,3;

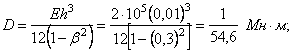
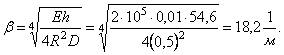
Получим , что составляет примерно треть диаметра цилиндрической оболочки.

Расчетный случай 3. Оболочка нагружена радиальной нагрузкой, распределенной на части длины цилиндра. Для этого случая может быть использовано решение предыдущего расчетного случая, если считать, что нагрузка , действующая на длине , (рис. 97) представляет собой погонную радиальную нагрузку Р.

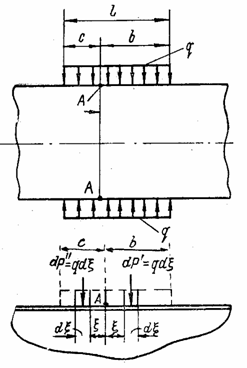
Рис. 97

Перемещения и усилия в какой-либо точке А от нагрузки вычисляются по формулам (5.60) - (5.63) и полученное выражение интегрируется по длине загруженного участка. Например, радиальное перемещение в точке А от элементарной нагрузки dP', расположенной справа от точки А,

,

а от нагрузки, приложенной на полосе шириной b справа от точки А,

.

Аналогичное выражение можно составить для перемещения от нагрузки, расположенной слева от точки А на полосе шириной с. Для перемещения от всей нагрузки, расположенной на полосе шириной l = с + b, получится выражение

. (5.64)

Интегрируя таким же образом выражения для , М_х и Q_x, возникающие от погонных радиальных сил , можно получить соответствующие выражения для этих величин от радиальной нагрузки, расположенной на полосе шириной l.

5.6 Длинная цилиндрическая оболочка, подкрепленная кольцами

Цилиндрическая оболочка, подкрепленная равноотстоящими кольцами, площадь сечения которых F, подвергается внешнему равномерно распределенному радиальному давлению интенсивностью q (рис. 98).

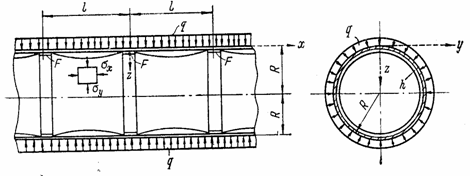
Рис. 98

Для нахождения усилий и перемещений в любом сечении следует наложить решение по схеме а (рис. 99), на решение по схеме б (расчетный случай 1).

Задача определения радиальных перемещений w для такой оболочки статически неопределима и для ее решения необходимо составить уравнение совместности деформаций.

1. Кольца абсолютно жесткие. Силу взаимодействия, возникающую между кольцом и оболочкой, обозначим X: погонная поперечная сила по схеме б

. (5.65)

Уравнение совместности деформаций

. (5.66)

Оно представляет собой условие того, что радиальное перемещение оболочки в сечении х = 0, в котором расположено кольцо, произойти не может.

а	б

Рис. 99

Перемещение оболочки от нагрузки q, которое было бы при отсутствии кольца, уничтожается перемещением оболочки , вызванным погонными усилиями Q₀ и M₀, возникающими в сечении х = 0 вследствие наличия в последнем подкрепляющего кольца. Верхние индексы “о” в формуле (5.56) показывают, что перемещения относятся к оболочке. Перемещение оболочки от нагрузки q по безмоментной теории [см. формулу (5.10)]:

.

По формуле (5.57) радиальное перемещение оболочки от действия погонной поперечной силы Q₀ и погонного изгибающего момента М_о

. (5.67)

Подставив указанные выражения (5.10) и (5.67) в уравнение (5.66), связывающее абсолютные значения перемещений, получим

.

Заменим Q₀ и M₀ в этом уравнении на неизвестные силы взаимодействия X. Поперечная сила Q₀ связана с Х зависимостью (5.65). Уравнение для замены М₀ на Х найдем из условия, что в силу симметрии изгиба оболочки касательная к изогнутой срединной поверхности оболочки в сечении х = 0 должна быть горизонтальна (см. рис. 98):

,

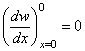или на основании формулы (5.58)

.

C учетом формулы (5.65)

. (5.68)

Подставим в уравнение (5.66) выражения Q₀ и М₀ (5.65) и (5.68) и получим

,

откуда

.

Так как при помощи выражения для коэффициента затухания перемещений можно написать

, (5.69)

то окончательное выражение для погонной силы взаимодействия:

. (5.70)

Тогда погонная поперечная сила Q₀ и изгибающий момент М₀ в сечении х = 0 по оси подкрепляющего кольца по формулам (5.65) и (5.68)

;

.

Такие же выражения Q₀ и М₀ получатся для цилиндрической оболочки, нагруженной радиальной сжимающей равномерно распределенной нагрузкой у защемленной кромки. Условия деформации у такой кромки те же, что и в случае абсолютно жесткого подкрепляющего кольца.

2. Кольца могут деформироваться. В этом случае уравнение совместности деформаций следует записать так:

. (5.71)

Оно отличается от уравнения (5.66), так как радиальное перемещение оболочки, представленное левой частью уравнения, уже неравно нулю. Разность абсолютных величин перемещений оболочки, вызванных нагрузкой q и погонными усилиями Q₀ и М₀, должна быть равна обжатию кольца , вызванному погонной силой взаимодействия Х (рис. 100).

Радиальное перемещение точек кольца от погонной нагрузки Х

.

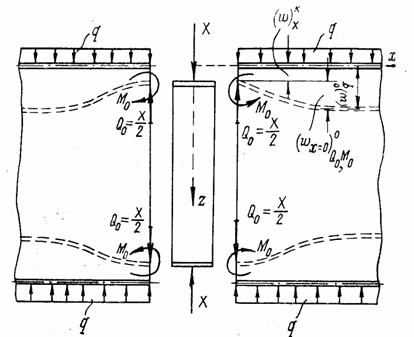
Рис. 100

Сжимающее напряжение в кольце (рис. 101)

,

поэтому

,

где F - площадь поперечного сечения кольца.

Выражения для Q₀ и М₀ через силу взаимодействия Х остаются такими же [см. формулы (5.65) и (5.68)], так как условия симметрии сохраняются.

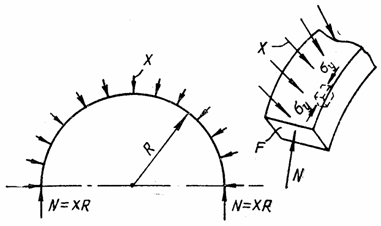
Рис. 101

Если учесть значения всех величин, входящих в уравнение (5.71) совместности деформаций, получится выражение

. (5.72)

Заменив его выражением (5.69), произведя сокращение на и решив уравнение (5.70) относительно X, получим

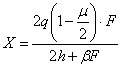. (5.73)

Представим решение (5.73) в виде произведения решения (5.70) для абсолютно жесткого кольца на коэффициент , учитывающий податливость кольца:

.

Коэффициент

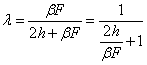
учитывает уменьшение погонной силы X, получающееся при деформации подкрепляющего кольца. Оно тем ближе к единице, чем меньше толщина оболочки h и чем больше площадь сечения кольца F.

Зная X, по формулам (5.65) и (5.68) находим поперечную силу и изгибающий момент Q₀ и M₀ в сечении, в котором расположено кольцо. Имея величины Q₀ и М₀, можно найти возникающие от них радиальные перемещения и усилия Q_x и М_x на любом расстоянии х от кольца, пользуясь формулами (5.53), (5.55) и (5.56).

5.7 Местные напряжения в сопряжении оболочек

Уравнение совместности деформации. При действии на оболочку равномерно распределенного давления в местах нарушения непрерывности меридионального сечения возникают местные усилия - изгибающие моменты и поперечные силы. Например, оболочка, показанная на рис. 102 состоящая из

q

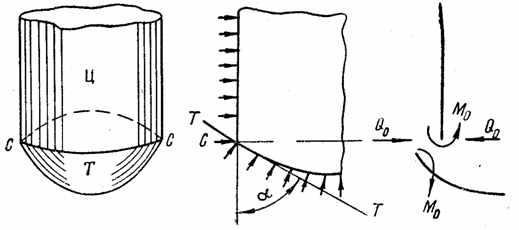
Рис. 102

цилиндрической части Ц и торцевой части Т в виде шарового сегмента, не имеет общей касательной в месте сопряжения этих частей. Поэтому по окружности СС их соприкосновения возникнут погонные усилия Q₀ и М₀ . Объясняется это тем, что линейные перемещения w и углы поворота касательных к изогнутой срединной поверхности, возникающие под действием равномерно распределенной нагрузки q, в общем случае различны для цилиндрической и торцевой частей оболочки. Для цилиндрической радиальные перемещения обычно больше, чем для торцевой, а угловые равны нулю. У торцевой части могут возникнуть угловые перемещения по окружности СС. Поэтому, если мысленно отделить торцевую часть от цилиндрической по

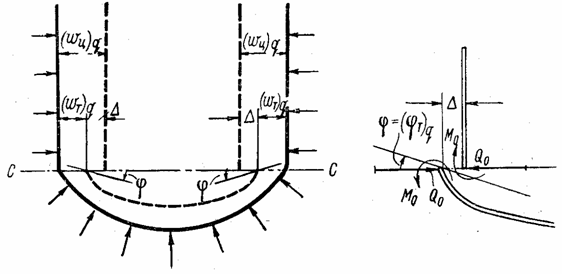
Рис. 103

сечению С - С (рис. 103), в сечении возникнут линейный разрыв

(5.74)

и угловой разрыв

, (5.75)

где и - радиальные перемещения цилиндрической и торцовой частей от нагрузки q;

- угловое перемещение торцевой части от нагрузки q.

Для уничтожения этих разрывов по сечению С - С необходимо приложить погонные поперечные силы Q₀ и изгибающие моменты М₀ . Эти усилия вызовут в сечении следующие смещения: погонная поперечная сила Q₀ - линейные смещения и и угловые смещения и погонный изгибающий момент M₀ - линейные смещения и и угловые смещения и . В общем случае эти смещения различны для торцевой и цилиндрической частей. Алгебраическая сумма линейных смещений должна равняться линейному разрыву , а алгебраическая сумма угловых смещений - угловому разрыву .

Таким образом, можно записать уравнения совместности деформаций (рис. 104)

(5.76)

. (5.77)

а б

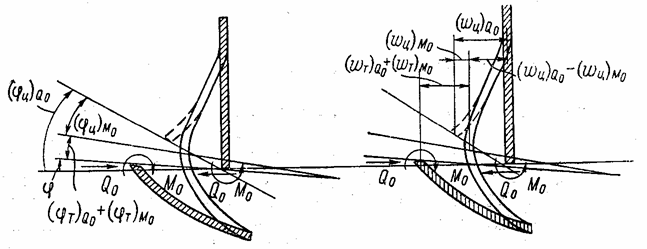
Рис. 104

Эти уравнения показывают, что возникающие в сечении С - С в непрерывной оболочке погонные усилия Q₀ и М₀ уничтожают линейный и угловой разрывы и и заставляют торцы цилиндрической и торцевой оболочек совпадать в переломе.

Приведенные рассуждения и уравнения (5.76) и (5.77) справедливы для сопряжения двух оболочек любого очертания и, в частности, для сопряжения цилиндрической оболочки с торцевой частью любого осесимметричного очертания - шарового, конического или плоского.

Сопряжение цилиндрической оболочки с полусферическим днищем. Определим усилия Q₀ и М₀ для наиболее простого сопряжения - цилиндрической оболочки с торцом в виде полусферы. В случае одинаковой толщины h цилиндрической и сферической частей можно считать, что по сечению С - С общая касательная для этих частей поворачивается в их сопряжении под действием усилий Q₀ на одинаковый угол и взаимный угол поворота отсутствует. Значит, в сечении С - С не возникает погонного изгибающего момента, т. е. М₀ = 0.

Остается только погонная поперечная сила Q₀, которую можно найти из решения геометрического уравнения (5.74), положив в нем члены, зависящие от М₀, равными нулю. Подставив в уравнение (5.74) абсолютные значения по формуле (5.10) и , найдем

. (5.78)

Приняв во внимание, что изгиб около сечения С - С местный и достигает значительной величины как в цилиндрической, так и в сферической оболочке лишь вблизи от места сопряжения, условно заменим сферическую оболочку цилиндрической. В таком случае, подставив в уравнение (5.76) абсолютные значения по формуле (5.57) (расчетный случай 1) при M₀ = 0 и по формуле (5.78), найдем

,

откуда

, (5.79)

или, подставив в формулу (5.79) значение по формуле (5.69)

Таким образом, в случае сопряжения цилиндрической и полусферической оболочек одинаковой толщины, нагруженных радиальной сжимающей нагрузкой интенсивностью q, можно принять

Сопряжение цилиндрической оболочки с плоским днищем. Оболочка нагружена внутренним радиальным давлением q. Плоское днище рассматривается как круглая пластина с радиусом R, нагруженная равномерным поперечным давлением q и погонным моментом М₀ по кромке. Ось х направлена по радиусу пластины.

Уравнение (5.60) углов поворота пластины

, (5.80)

где D₁ - цилиндрическая жесткость пластины.

В центре пластины при х = 0, угол наклона касательной плоскости равен нулю, поэтому первое граничное условие = 0 при х = 0, откуда С₂ = 0.

Выражение для радиального погонного изгибающего момента

.

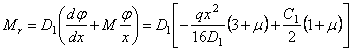На контуре пластины

.

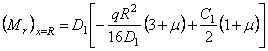Этот погонный момент должен равняться и быть противоположным по знаку погонному моменту M₀, действующему по кромке оболочки, поэтому второе граничное условие (M_r)_x=R = M₀, откуда

. (5.81)

Подстановка значения С₂ = 0 и C₁ по формуле (5.81) в уравнение (5.80) даст следующее значение для угла поворота на контуре пластины:

.

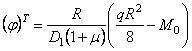Радиальный изгибающий момент в произвольном сечении пластины на расстоянии х от центра

.

Если считать радиальное перемещение пластины пренебрежимо малым в уравнении совместности (5.76), можно принять . Тогда оно примет вид

.

Учитывая, что

,

полу чим

или, после подстановки радиальных перемещений w_Ц ,

, (5.82)

где D — цилиндрическая жесткость оболочки.

Уравнение (5.77) примет вид:

. (5.83)

Уравнения (5.82) и (5.83) содержат две неизвестные величины: М₀ и Q₀. Решая систему, находим погонную поперечную силу и изгибающий момент в сопряжении оболочки с плоским торцом

; (5.84)

. (5.85)

Пользуясь выражениями радиальных смещений w и углов поворота сечений оболочек и уравнениями (5.76) и (5.77) совместности деформаций, можно аналогичным путем вывести формулы для погонных поперечных сил Q₀ и погонных изгибающих моментов М₀ , возникающих в сопряжении цилиндрической оболочки с торцевой, имеющей форму полусферы, шарового сегмента, конуса или плоской пластины, при различных толщинах оболочки в цилиндрической и торцевой частях. Зная Q₀ и М₀, можно вычислить w_x, Q_x и М_х в любой точке цилиндрической части, пользуясь формулами (5.33), (5.55), (5.56).

5.8 Определение перемещений и усилий в короткой цилиндрической оболочке

Выше (расчетный случай 2) указывалось, что когда расстояние l между торцами или подкрепляющими кольцами цилиндрической оболочки меньше отношения , усилия и перемещения в оболочке следует определять, учитывая ее ограниченную длину. В этом случае удобнее пользоваться для интеграла дифференциального уравнения равновесия элемента (5.32) формулой (5.34), а не (5.33), а начало координат располагать в середине длины оболочки.

Кроме того, для определения произвольных постоянных интегрирования должны быть составлены другие граничные условия. Например, первое условие для расчетного случая 1, составленное в предположении равенства нулю радиального перемещения w при абсциссе х, стремящейся к бесконечности, не может быть использован для короткой оболочки, но имеется возможность использовать граничные условия на обоих торцах оболочки.

Для примера составим уравнение изогнутой срединной поверхности для нагрузки Q₀ и M₀ (см. расчетный случай 1), приложенной к короткой оболочке (рис. 105). Так как интенсивность нагрузки q = 0, уравнение изогнутой срединной поверхности в соответствии с формулой (5.34)

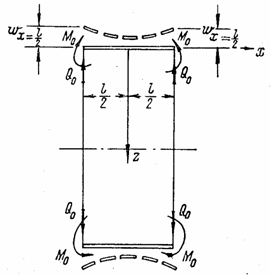
Рис. 105

Постоянные A определяем из следующих граничных условий:

Так как каждое из последних двух условий объединяет в себе два условия (плюс или минус ), число уравнений, необходимых для определения постоянных А, достаточно. Усилия и перемещения в коротких оболочках удобно выражать с помощью тригонометрических и гиперболических функций от .

5.9 Температурные напряжения в цилиндрической оболочке

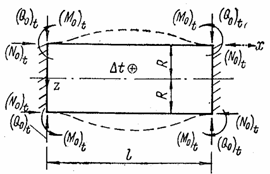
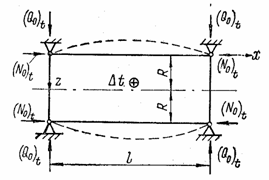
1. Одинаковое постоянное изменение температуры во всех направлениях. Если торцы оболочки свободны и деформация ее как в радиальном направлении, так и вдоль образующей не стеснена, напряжения при равномерном изменении температуры не возникают. При любом способе симметричного закрепления торов (рис. 106) в торцевом сечении возникают те или иные реактивные погонные усилия: изгибающие моменты (M₀)_t, продольные (N₀)_t и поперечные (Q₀)_t силы.

а	б

Рис. 106

Для нахождения изгибающих моментов и поперечных сил, возникающих при изменении температуры на , приравняем радиальные температурные перемещения, равные абсолютному изменению длины радиуса,

радиальным перемещеням w_x=0 в сечении х = 0, вызванным погонными моментами (M₀)_t и поперечными силами (Q₀)_t [см. формулу (5.57)]. Получим уравнение

, (5.86)

содержащее два неизвестных: .

Второе уравнение, содержащее эти два неизвестных, получится из условия равенства нулю угла наклона касательной к оси х в защемлении (рис. 106,а) или в середине пролета (рис. 106,б). Для защемленной оболочки (рис. 106,a) это условие запишется по формуле (5.58)

, (5.87)

для опертой оболочки (рис. 106,б) - по формуле (5.54)

. (5.88)

Решая совместно уравнения (5.86) и (5.87) или (5.86) и (5.88), можно найти усилия (M₀)_t и (Q₀)_t, а затем w, Q_x и М_x в любом сечении с помощью формул (5.53), (5.55) и (5.56).

Погонная продольная сила (N_x)_t, возникающая при закреплении торцов оболочки, определяется из условия совместности деформации вдоль оси х

откуда

.

2. Постоянная разность температур в радиальном направлении. Обозначим через t₁ температуру на внутренней поверхности оболочки и через t₂ - на наружной. В сечениях, удаленных от закрепленных торцов, или в случае, если торцы свободны, местного изгиба нет. Предположим, что температура и вызванные ею относительные линейные деформации изменяются по толщине h оболочки по линейному закону (рис. 107). Примем t₂ > t₁ и обозначим

.

Относительная температурная деформация наружного волокна оболочки

.

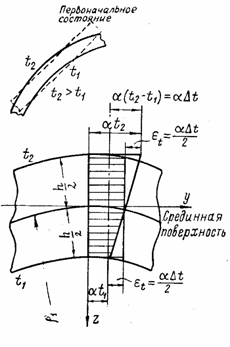
Рис. 107

С другой стороны, эта же деформация, на основании гипотезы плоских сечений

,

где - радиус образующих цилиндра при изгибе.

Приравняв эти выражения друг другу, получим кривизну

. (5.89)

В то же время искривление образующей цилиндрической оболочки под действием изгибающего погонного момента М_х характеризуется кривизной [см. формулу (5.26)]

. (5.90)

Если торец защемлен, искривления образующей не происходит, погонный изгибающий момент М_х находим, приравнивая выражения (5.89) и (5.90):

Наибольшие нормальные напряжения в крайних волокнах

. (5.91)

В случае t₂ > t₁ знак плюс соответствует наружной поверхности оболочки, знак минус - внутренней. Около закрепленных торцов возникает местный изгиб, и на напряжение по формуле (5.91) алгебраически накладываются напряжения, вычисленные по значению, из условия удовлетворения граничным условиям.

3. Постоянная разность температур в направлении оси х. Изменение температуры вдоль оси х вызывает изгиб оболочки, обусловленный различными радиальными перемещениями поперечных сечений. Он может описываться дифференциальным уравнением, аналогичным уравнению(5.32), если подставить в него переменную интенсивность q, вызывающую такие же деформации, как и переменная температура.

Примем закон изменения температуры по длине оболочки

Относительное окружное напряжение по закону Гука

а погонная продольная сила

.

С другой стороны, N_у = —qR (см. рис. 101), откуда интенсивность радиальной нагрузки, эквивалентной температурному воздействию,

.

Подстановка этого значения в уравнение (5.32) дает

(5.92)

и задача сводится к интегрированию дифференциального уравнения (5.92).

5.10 Напряженное состояние цилиндрической оболочки и условие прочности

Наибольшие напряжения в цилиндрической оболочке складываются алгебраически из напряжений мембранных, напряжений от изгиба моментами М_х и M_y и температурных напряжений , если они есть. Пренебрегая напряжениями = ± q малыми по сравнению с напряжениями и (см. рис. 92), элемент оболочки, выделенный двумя меридиональными и двумя экваториальными сечениями, можно считать испытывающим плоское деформированное состояние.

Так как касательные напряжения

то нормальные напряжения и представляют собой главные напряжения. Наибольшее нормальное напряжение, действующее по поперечному сечению цилиндра и направленное вдоль образующей (см. рис. 92), возникает на одной из поверхностей оболочки и вычисляется как алгебраическая сумма

(5.93)

Знаки плюс или минус в выражении (5.93) зависят от направления нагрузки q, характера изменения температуры и расположения точки, в которой определяется напряжение на внутренней или наружной поверхности оболочки.

Наибольшее нормальное напряжение, действующее по радиальному сечению и направленное по касательной к окружности,

(5.94)

В уравнении (5.94) последний член представляет собой напряжение, вызванное обжатием оболочки вследствие радиального перемещения w_x,

Алгебраически большее из двух отрицательных напряжений, вычисленных по формулам (5.93) и (5.94), в случае наружного давления будет главным напряжением , меньшее - главным напряжением . Главное напряжение равно нулю. В случае внутреннего давления главное напряжение s₁ равно алгебраически большему из двух положительных напряжений, равно меньшему, a равно нулю. Поэтому в условии прочности по третьей теории прочности

одно из слагаемых в левой части при любом нагружении равно нулю и условие прочности будет

.

По четвертой теории прочности условие прочности при внутреннем давлении

.

Найдем, например, главные напряжения и составим условие прочности для цилиндрической оболочки, подвергнутой наружному давлению q, считая температурные воздействия отсутствующими.

В сопряжении цилиндра с торцом мембранные напряжения сжимающие, напряжения от изгиба у торца растягивающие на наружной поверхности оболочки и сжимающие на внутренней, напряжения от обжатия сжимающие. Поэтому на внутренней поверхности

а на наружной поверхности, с учетом того, что местные напряжения больше мембранных и возникающих от обжатия,

Так как на внутренней поверхности абсолютная величина нормальных напряжений больше, чем на наружной, условие прочности примет вид

.

Местные напряжения от краевого эффекта не всегда следует считать расчетными. Для пластических материалов концентрация местных напряжений, превышающих допускаемые, захватывающая небольшой участок конструкции, при статическом постоянном действии нагрузки иногда допускается. Если же такое перенапряжение происходит периодически, например при многократном повышении и спаде давления, оно может вызвать возникновение усталостной трещины именно в зоне концентрации и не может быть допущено. Расчетными считаются также местные напряжения и для оболочек, выполненных из хрупких материалов.

В ряде случаев при наружном давлении размеры оболочки лимитируются не рассмотренными условиями прочности, а условиями устойчивости. Оболочки нередко должны дополнительно удовлетворять требованиям стойкости в коррозионно-агрессивных средах и при других химических воздействиях. Для оболочек, подверженных действию высокой температуры, допускаемое напряжение следует назначать с учетом возможной ползучести материала.

5.11 Примеры

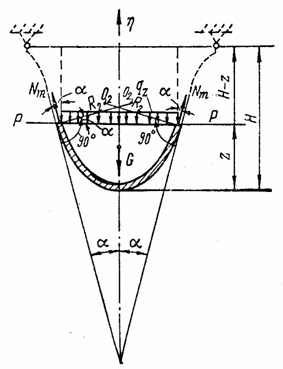
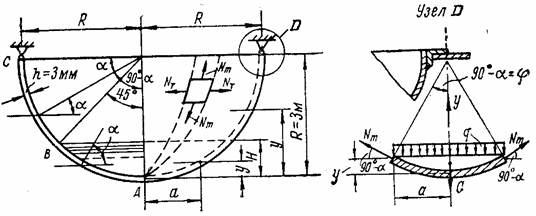
Пример 5.1. Тонкостенный сосуд, выполненный в виде полусферы, свободно закреплен по диаметральной окружности и частично нагружен, как показано на рис. 108,а, жидкостью с объемным весом = 0,01 Мн/м³. Пренебрегая собственным весом сосуда, построить эпюры изменения главных напряжений и в его стенке.

Решение.

Рассмотрим отдельно участок сосуда, испытывающий давление жидкости, и участок, не испытывающий этого давления.

1. 45 < < 90° (участок ВА).

Из условия равновесия отсеченного от сосуда сегмента, показанного на рис. 108,б, по формуле (5.4) меридиональное погонное усилие

.

Вес жидкости G равен объему шарового сегмента высотой у, умноженному на объемный вес:

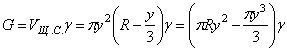. (5.95)

Выразим радиус R через у и а. Из прямоугольного треугольника

откуда

.

а	б
в	г

Рис. 108

Подставим это выражение в формулу (5.95):

.

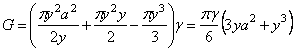Учитывая, что , получим

.

Выразим через R и интенсивность нагрузки q:

.

Подстановка найденных выражений для G и q в формулу (5.4) даст погонное меридиональное усилие

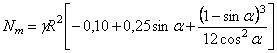. (5.96)

Общий множитель, если R₁ = R₂ = R = 3 м,

.

Окружное погонное усилие N_Т находим из уравнения Лапласа (5.3):

или, подставляя вместо q его выражение,

. (5.97)

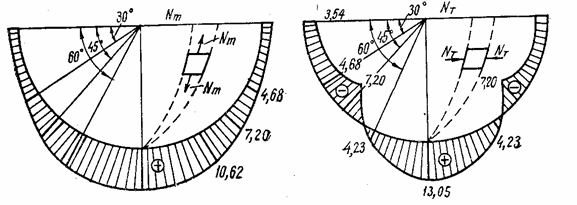
Таблица 5

, град	sin	cos	(1-cos )^3	cos^3	0,25sin	(1-sin )^3 12cos^2	Nm R^2	Nm×10^3, Мн/м	Формула
0	-	1,000	-	1,000	-	-	-	3,54	(5.98)
30	-	0,870	-	0,755	-	-	-	4,08	(5.98)
45	0,705	0,705	0,0256	0,496	0,176	0,0040	0,080	7,20	(5.98); (5.96)
60	0,870	0,500	0,0022	0,250	0,217	0,0007	0,118	10,62	(5.96)
90	1,000	0	0	0	0,250	0	0,150	13,50	(5.96)

2. 0 < < 45⁰ (участок СВ).

Высота жидкости в сосуде

Вес G жидкости в сосуде

.

Таблица 6

, град	Nm×10^3, Мн/м	sin - 0,707	R^2(sin - - 0,707) × 10^3, Мн/м	NT×10^3, Мн/м	Формула
0	3,54	-	-	-3,54	(5.99)
30	4,68	-	-	-4,68	(5.99)
45	7,20	0	0	-7,20	(5.99); (5.97)
60	10,62	0,165	14,85	+4,23	(5.97)
90	13,50	0,295	26,55	+13,05	(5.97)

Погонное меридиональное усилие

. (5.98)

Погонное окружное усилие N_T найдем из уравнения Лапласа:

. (5.99)

Оно равно по величине и противоположно по знаку меридианальному.

Результаты подсчета погоных усилий представлены в табл. 5 и 6. По данным этих таблиц построены эпюры усилий N_m и N_T (рис. 108,в, г).

Пример 5.2. Цилиндрический стальной корпус, имеющий подкрепляющие кольца и торцы (рис. 109), подвержен внутреннему давлению q = 2 Мн/м². Построить эпюры меридиональных изгибающих моментов М_х вблизи от подкрепляющих колец в двух предположениях: 1) кольца абсолютно жесткие; 2) кольца упругие. Модуль упругости Е= 2× 10⁵ Мн/м²; = 0,3.

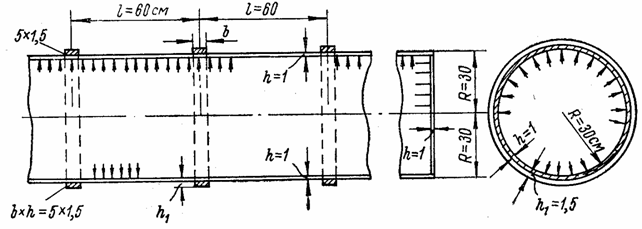
Рис. 109

Решение.

1. Вычисление вспомогательных величин.

Цилиндрическая жесткость

.

Коэффициент затухания

.

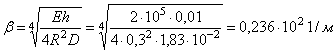Длина оболочки, при которой ее можно считать длинной,

Так как l = 0,6 > 0,266 м, можно не учитывать совместное влияния двух подкрепляющих колец на расположенную между ними оболочку и вести расчет по формулам для длинной оболочки. В формулы, выведенные для цилиндрической оболочки, подверженной наружной нагрузке интенсивностью q, нужно интенсивность подставлять со знаком минус.

2. Определим изгибающие моменты М_х в предположении, что кольца абсолютно жесткие.

Сила взаимодействия между кольцами и оболочкой по формуле (5.70)

.

Погонная поперечная сила Q на оси кольца

.

Погонный изгибающий момент М₀ на оси кольца

.

Ординаты эпюры погонных изгибающих моментов

или после упрощения

.

Функции и берутся из табл. 4. В табл. 7 представлены результаты вычислений ординат М_х. По данным таблицы построена эпюра на рис. 110.

Таблица 7

№ точки		х, см			1,52, Мн	3,05, Мн	Мх, Мн
0	0	0	1,0000	0	1,520	0	1,520
1	0,2	0,85	0,9651	0,1627	1,464	0,495	0,966
2	0,4	1,65	0,8784	0,2610	1,332	0,795	0,537
3	0,6	2,54	0,7628	0,3099	1,160	0,945	0,215
4	0,8	3,40	0,6354	0,3223	0,965	0,982	-0,017
5	1,0	4,25	0,5083	0,3095	0,775	0,945	-0,170
6	1,5	6,34	0,2384	0,2226	0,363	0,680	-0,317
7	2,0	8,50	0,0667	0,1230	0,101	0,375	-0,274
8	2,5	10,6	-0,0166	0,0492	-0,025	0,160	-0,175
9	3,0	12,7	-0,0423	0,0071	-0,064	0,022	-0,086
10	4,0	16,9	-0,0258	-0,0139	-0,039	-0,042	+0,003
11	5,0	21,2	-0,0046	-0,0065	-0,007	-0,0020	+0,013

Положение нулевых точек эпюры изгибающих моментов (см. рис. 110) определяется расстоянием

После второй нулевой точки, на расстоянии 3,33 + 13,33 = 16,66 см от оси кольца, изгибающие моменты уменьшаются до величины

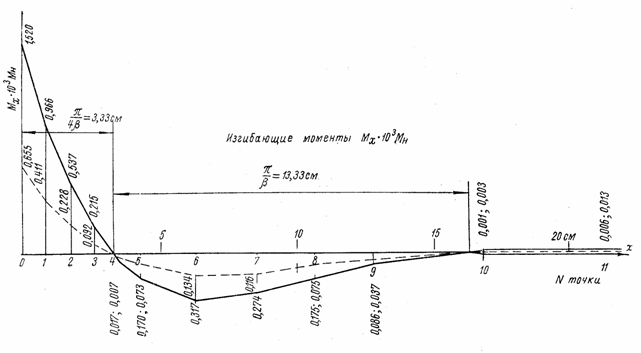
Рис. 110

и вызывают напряжение

Это напряжение настолько мало, что его можно не учитывать.

3. Определяем изгибающие моменты М_х в предположении, что кольца упругие. Моменты М_х пропорциональны краевому изгибающему моменту М₀ и краевой поперечной силе Q₀, которые, в свою очередь, пропорциональны силе взаимодействия Х. Поэтому ординаты эпюры М_х получаются путем умножения ординат эпюры M_х, вычисленных в табл. 7, на коэффициент

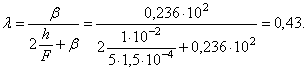
Таким образом, при учете податливости колец погонные изгибающие моменты составляют лишь 43% от моментов, вычисленных в предположении жестких колец. Соответствующая эпюра изгибающих моментов М_х построена на рис. 110 штриховой линией.

Пример 5.3 Для оболочки, рассмотренной в предыдущем примере, построить эпюры погонных изгибающих моментов М_х и погонных поперечных сил Q_x в месте примыкания оболочки к плоскому торцу, возникающих от внутреннего давления q = 50 н/см², вычислить главные напряжения и и составить условие прочности по третьей теории прочности. Допускаемое напряжение = 40 000 н/см².

Решение.

По табличным формулам находим значения погонных краевых изгибающих моментов М₀ и поперечных сил Q₀ для случая примыкания цилиндрической оболочки к плоскому торцу, приняв следующие исходные данные:

- геометрические размеры

h₁ = h₂ = h = 1 cм; R = 30 см;

- упругие постоянные Е = 2 н/см²; = 0,3;

D₁ = D₂ = D = 1,83 нсм;

- интенсивность радиальной нагрузки

q = 50 н/cм²;

- коэффициент затухания перемещений

0,236 1/см.

Погонный изгибающий момент в сечении оболочки, примыкающем к торцу, вычисляется по формуле(5.85):

Погонная поперечная сила в этом сечении вычисляется по формуле (5.84)

Зная М₀ и Q₀, можно вычислить погонные изгибающие моменты М_х и погонные поперечные силы Q_х вдоль образующей х:

Функции , и берутся из табл. 4. В табл. 7 представлены результаты вычислений ординат изгибающих моментов М_х и поперечных сил Q_х. По данным таблицы построены эпюры на рис. 111. Положение нулевых точек эпюры Q_х определяется расстояниями (х₀)₁ = 1,25 см и (х₀)₂ = 14,8 см. В этих сечениях изгибающие моменты достигают максимума.

Таблица 8

№ точки		х, см				5170	1258	5325	2440	Мх, нсм/см	Qx, н/см
1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	1,000	0	1,000	5170	1258	0	0	5170	1258
1	0,2	0,85	0,9653	0,1627	0,6398	5000	802	870	480	5870	-322
2	0,4	1,65	0,8784	0,2610	0,3564	4537	448	1390	770	5927	322
3	0,6	2,54	0,7628	0,3099	0,1431	3940	180	1650	912	5590	732
4	0,8	3,40	0,6354	0,3223	0,0093	3284	-12	1720	952	5004	964
5	1,0	4,25	0,5083	0,3096	0,1108	2625	-136	1650	915	4275	1051
6	1,5	6,34	0,2384	0,2226	-0,2068	1237	-260	1188	657	2425	917
7	2,0	8,5	0,0667	0,1230	-0,1794	345	-226	655	362	1000	588
8	2,5	10,6	-0,0166	0,0492	-0,1149	-86	-144	262	145	176	289
9	3,0	12,7	-0,0423	0,0071	--0,0563	-218	-70	37	21	-181	91
10	4,0	16,9	-0,0258	-0,0139	0,0019	-134	2	-74	-41	-208	-43
11	5,0	21,2	-0,0046	-0,0065	0,0084	-24	10	-34	-19	-58	-29

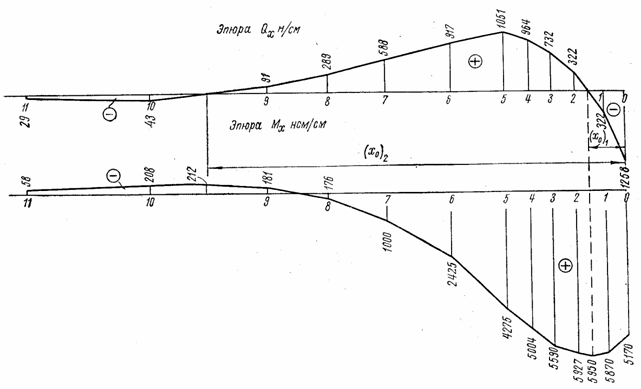
Рис. 111

Изгибающий момент в плоском днище вычисляется как для круглой пластины, нагруженной по контуру погонными радиальными моментами. Эти моменты постоянны по диаметру торца и вызывают шаровой изгиб. Кроме того, на торец действует равномерно распределенная нагрузка интенсивностью q. Она вызывает изгибающие моменты M_r, показанные на рис. 112.

В центре днища от нагрузки q

Эпюру радиальных изгибающих моментов строим по принципу независимости действия сил как суммарную эпюру моментов, возникающих под действием моментов М₀ и нагрузки q.

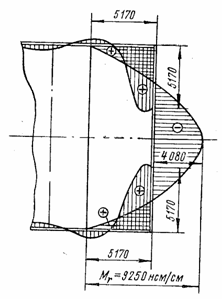
Рис. 112

Наиболее напряженная точка находится на расстоянии (х₀)₁=1,25 см от места примыкания цилиндрической оболочки к торцу. В этом месте действуют погонные усилия:

M_y = mM_x = 0,3 × 5950 = 1780 (н× см)/см;

Для определения четвертого члена в формуле (5.94) для экваториального (окружного) нормального напряжения необходимо вычислить радиальное перемещение w_x в сечении, в котором производится вычисление напряжений:

Наибольшие главные нормальные напряжения:

- меридиональное, действующее вдоль образующей, по формуле (5.93)

- экваториальное, действующее вдоль окружности, поперечного сечения, по формуле (5.94)

Условие прочности по третьей теории прочности при :

Пример 5.4. Для цилиндрической оболочки, нагруженной радиальной равномерно распределенной нагрузкой интенсивностью q = 30 н/см и защемленной концами (рис. 113,а), вычислить ординаты перемещений w_x по радиусу и построить изогнутую срединную поверхность. Материал – титан. Модуль упругости Е= 1,1; коэффициент Пуассона = 0,3.

Решение.

Цилиндрическая жесткость

Коэффициент затухания перемещений

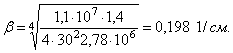
Отношение

следовательно, оболочка длинная.

Перемещения w находим наложением решений для незащемленной оболочки, нагруженной радиальным давлением q (рис. 113,в), и для оболочки, нагруженной усилиями М₀ и Q₀ на торцах (рис. 113,б).

а	б
	в

Рис. 113

Условие совместности деформации

Условие защемления - равенство нулю угла наклона касательной к оболочке в защемлении:

Эти два условия такие же, как для оболочки, подкрепленной абсолютно жесткими кольцами. Поэтому выражения для изгибающего момента М₀ и поперечной силы Q₀ в защемлении те же, что и для подкрепленной оболочки:

Зная эти усилия, перемещения в любой точке можно вычислить по формуле

Первый член в этой формуле вычисляется согласно (5.48), а второй

Характер изогнутой средней поверхности показан на рис. 113.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00