Главная
Лекция 4. Пластины, мембраны
4.1 Основные определения и допущения
Пластиной
называется тело призматической или цилиндрической формы, у которого один
размер (толщина h)
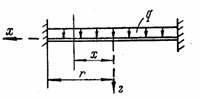
значительно меньше других (а и b), измеренных в плоскостях оснований (рис. 39). В технике
широко используются круглые и прямоугольные пластины; иногда встречаются
пластины и других очертаний в плане. Толщина пластины может быть как
постоянной, так и переменной.
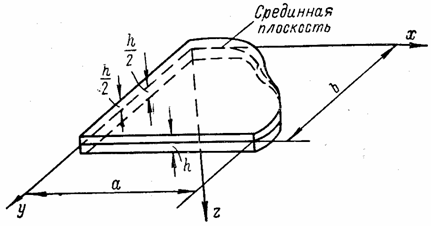
Рис. 39
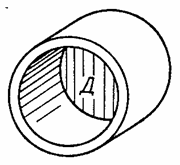
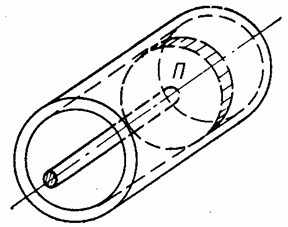
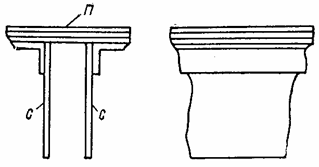
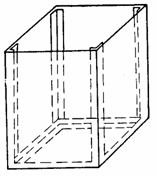
Примером круглой пластины может служить днище Д цилиндрического сосуда - бака, котла, трубы (рис. 40,а) - или поршень П, движущийся в цилиндре (рис. 40,б). Примером прямоугольной пластины, защемленной одной кромкой, может служить каждая из вертикальных стенок с сечения, составленного из листов, при значительной жесткости полки п (рис. 40,в), а примером пластины, упруго защемленной тремя кромками, - стенка прямоугольного резервуара (рис. 40,г).
Плоскость, находящаяся на равных расстояниях от верхнего и нижнего оснований и делящая пополам толщину h пластины постоянной толщины (рис. 39), называется срединной плоскостью. После изгиба срединная плоскость превращается в срединную поверхность изогнутой пластины.
При изучении пластин принимается система координат, при которой начало координат и оси х и у лежат в недеформированной срединной плоскости пластины, а ось z направлена перпендикулярно к срединной плоскости. В общем случае на пластину могут действовать различно направленные силы. Каждую из этих сил можно разложить на две составляющие: действующую в срединной плоскости и перпендикулярную к ней. Совокупность составляющих усилий в срединной плоскости, называемых цепными усилиями, вызывает деформацию только в этой плоскости, а совокупность составляющих, перпендикулярных к срединной плоскости, изгибает пластину. В дальнейшем предполагается, что нагрузка, испытываемая пластиной, перпендикулярна к ее срединной плоскости, т. е. составляющие нагрузки в срединной плоскости равны нулю.
|
а |
б |
|
|
|
|
в |
г |
|
|
|
Рис. 40
При определении усилий и деформаций для пластин средней толщины принимаются следующие допущения:
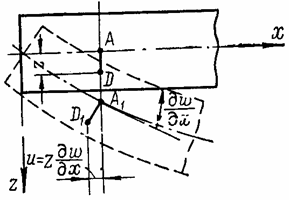
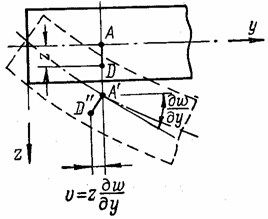
1. Перпендикуляр AD к срединной плоскости, опущенный из любой точки D пластины (рис. 41), остается после изгиба прямым и нормальным к изогнутой срединной поверхности (А1D1). Это допущение, называемое допущением о прямых нормалях, соответствует гипотезе плоских сечений, на котором основана теория изгиба балок.
Влияние на
величину перемещений некоторого искривления нормали, происходящего вследствие
сдвигов, не учитывается. Оно значительно меньше, чем перемещения ![]() или
или ![]() , вызываемые поворотом нормали вследствие искривления
срединной плоскости при изгибе.
, вызываемые поворотом нормали вследствие искривления
срединной плоскости при изгибе.
2. Нормальными
напряжениями ![]() , действующими по площадкам, параллельным срединной
плоскости, можно пренебречь по сравнению с другими напряжениями и принять
, действующими по площадкам, параллельным срединной
плоскости, можно пренебречь по сравнению с другими напряжениями и принять
![]() (4.1)
(4.1)
Это допущение
называется допущением об отсутствии поперечного давления.
|
|
|
Рис. 41
Для относительных деформаций можно использовать формулы
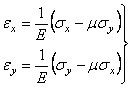 .
(4.2)
.
(4.2)
При изучении поперечного изгиба пластины средней толщины считаем: 1) срединную плоскость свободной от цепных усилий, 2) линейные и угловые деформации в срединной поверхности изогнутой пластины - отсутствующими. Перечисленные допущения применимы только при малом прогибе пластины.
Пластину можно условно отнести к тому или иному виду в зависимости от отношения толщины h к наименьшему размеру а пластины в плане (рис. 39). Существует три вида пластин, принципиально отличающихся друг от друга характером распределения напряжений и способом расчета:
1.
Плиты - толстые пластины, имеющие
отношение
![]()
У этих пластин
(рис. 42) высота настолько велика по
сравнению с пролетом и они настолько жестки, что касательные напряжения ![]() , возникающие по сечениям С - С от перерезывания
под действием нагрузки, имеют тот же порядок, что и нормальные напряжения
, возникающие по сечениям С - С от перерезывания
под действием нагрузки, имеют тот же порядок, что и нормальные напряжения ![]() , вызванные изгибом. Плоскость, свободная от цепных усилий и
от деформаций, смещается по отношению к срединной плоскости, а нормальные
напряжения распределяются по высоте сечения уже не по прямолинейному, а по
криволинейному закону.
, вызванные изгибом. Плоскость, свободная от цепных усилий и
от деформаций, смещается по отношению к срединной плоскости, а нормальные
напряжения распределяются по высоте сечения уже не по прямолинейному, а по
криволинейному закону.
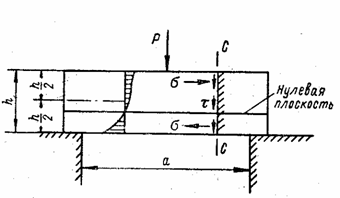
Рис. 42
Допущения, перечисленные выше, при расчете плит неприменимы.
2. Пластины средней толщины, имеющие отношение
![]()
Под действием сил, перпендикулярных к срединной плоскости, пластина изгибается, но вследствие достаточной жесткости прогиб w (рис. 43) не превосходит толщины h и опертая пластина способна нести вертикальную нагрузку. Эпюра нормальных напряжений в сечениях, перпендикулярных к срединной плоскости, прямолинейна. Характерная особенность изгиба пластин нагрузкой, нормальной к срединной плоскости, заключается в том, что он нередко сопровождается кручением.
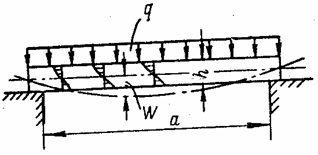
Рис. 43
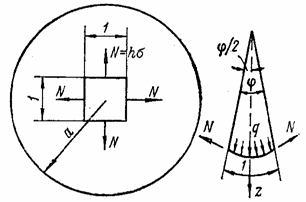
3. Мембраны - пластины, имеющие отношение
![]()
Мембраны тонки и гибки, поэтому, чтобы они могли нести нагрузку, нормальную к срединной поверхности, их часто закрепляют на контуре (рис. 44).
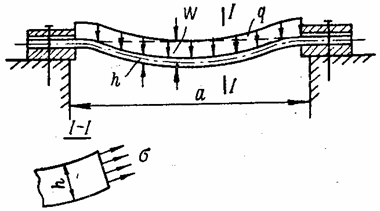
Рис. 44
При этом
нагрузка поддерживается мембраной в основном не за счет ее изгиба, а за счет
растяжения по всей толщине. Таким образом, можно считать, что нормальные
напряжения распределяются равномерно по толщине мембраны и срединная
поверхность не свободна от напряжений. Прогибы w мембраны
велики и могут в несколько раз превышать ее толщину h.
Мембраны широко применяются в различных акустических аппаратах и гидравлических устройствах.
В зависимости от характера конструкции любая кромка пластины (рис. 45)
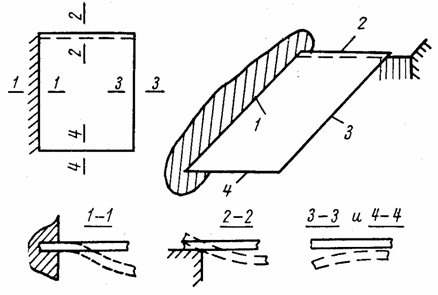
Рис. 45
может быть защемлена (кромка 1), свободно оперта (кромка 2) или свободна от закреплений
(кромки 3 и 4). Возможно также
упругое закрепление кромки пластины, промежуточное между свободной кромкой и
защемлением, которое дает возможность срединной поверхности под действием
нагрузки в той или иной степени поворачиваться на упруго защемленной кромке.
Примыкание кромки пластины 1 к
любому упругому элементу 2
(рис. 46) представляет собой упругое ее закрепление; возможный угол поворота ![]() на кромке обратно
пропорционален жесткости элемента 2,
к которому она прикреплена.
на кромке обратно
пропорционален жесткости элемента 2,
к которому она прикреплена.
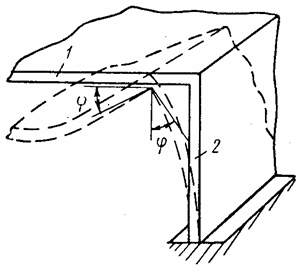
Рис. 46
Указанный выше признак деления пластин на плиты, пластины средней толщины и мембраны следует считать условным. Главное различие между этими классами заключается в соотношении между величиной цепных и изгибных усилий, которое может быть установлено только расчетом. Одна и та же пластина в зависимости от величины отношения продольных сил к изгибающим моментам и от способа закрепления на контуре может быть отнесена к тому или иному классу.
Цепные продольные усилия, вызывающие равномерно распределенные по толщине напряжения, могут появиться при поперечном нагружении пластины, закрепленной на контуре, вследствие препятствий, которые оказывают опоры сближению кромок пластины.
Наличие
продольных усилий сказывается на элементах изгиба: прогибы, изгибающие моменты
и поперечные силы тем больше, чем меньше отношение ![]() . Растягивающие продольные силы уменьшают, а сжимающие
увеличивают элементы изгиба от заданной поперечной нагрузки. Это влияние для
защемленной на контуре пластины меньше, чем для опертой.
. Растягивающие продольные силы уменьшают, а сжимающие
увеличивают элементы изгиба от заданной поперечной нагрузки. Это влияние для
защемленной на контуре пластины меньше, чем для опертой.
4.2 Дифференциальное уравнение изогнутой срединной поверхности пластины
в прямоугольных координатах
В общем случае изгиба пластины произвольного очертания нагрузкой q (х, у), распределенной на ее поверхности по произвольному закону (рис. 47),
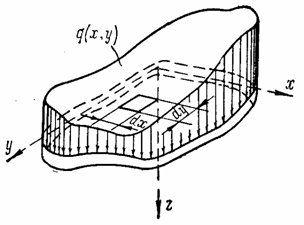
Рис. 47
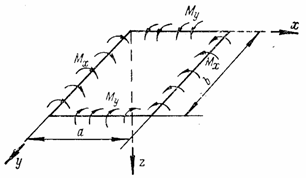
по граням прямоугольного элемента, имеющего размеры dx и dy в плане, выделенного из пластины двумя парами сечений, действуют погонные изгибающие моменты Мх и Mу, погонные поперечные силы Qx и Qy и погонные крутящие моменты Нx и Нy (рис. 48).
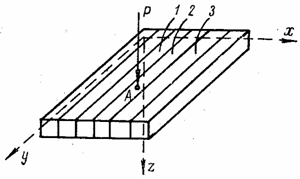
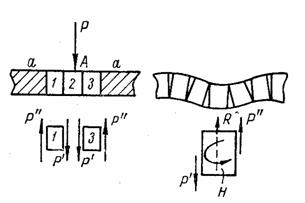
Возникновение крутящих моментов можно объяснить так. Если рассечь опертую по контуру пластину на ряд полос 1, 2, 3, .... (рис. 49,а), каждая из которых представляет собой балку, опертую по концам, то сила Р, приложенная к точке А пластины, вызовет прогиб только той балки 2, к которой относится точка А. В пластине, не рассеченной на полосы, полоса 2 поддерживается соседними полосами 1 и 3, которые в свою очередь испытывают со стороны полосы 2 направленные вниз усилия Р' (рис. 49,б). Со стороны примыкающих к полосам 1 и 3 частей а пластины эти полосы испытывают поддерживающее усилие Р". Усилия Р' и Р", действующие на каждую из полос 1 и 3, можно привести к равнодействующей R, приложенной в центре тяжести сечения полосы, и к паре Н, скручивающей полосу (рис. 49,б).
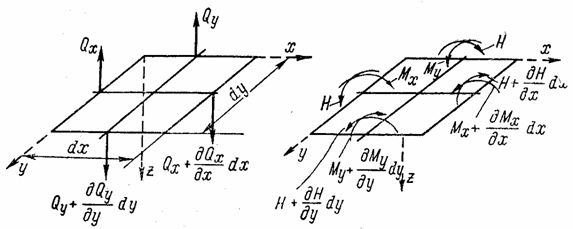
Рис. 48
|
а |
б в |
|
|
|
Рис. 49
Задачу решаем
в перемещениях. Из первого допущения теории пластин о возможности пренебречь
относительными сдвигами ![]() и
и ![]() ,
,
![]() (4.3)
(4.3)
На основании второго допущения w не зависит от z. Интегрируя равенства (4.3) по z, находим
![]()
или, так как при z = 0 у нас u = v = 0,
![]() (4.4)
(4.4)
С учетом зависимостей (4.4) относительные деформации выразятся через перемещение w следующим образом:
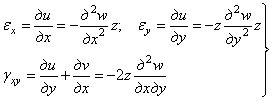 .
(4.5)
.
(4.5)
Так как на
основании второго допущения напряжением ![]() можно пренебречь, из
формул (1.20) закона Гука, полагая
можно пренебречь, из
формул (1.20) закона Гука, полагая ![]() = 0 и учитывая
выражения (4.5), получаем
= 0 и учитывая
выражения (4.5), получаем
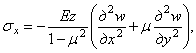 (4.6)
(4.6)
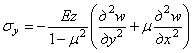 , (4.7)
, (4.7)
![]() . (4.8)
. (4.8)
Пользуясь
дифференциальными уравнениями равновесия (1.2), можно найти также напряжения ![]() . Хотя мы условились считать их малыми, но производные этих
напряжений, входящие в уравнения (1.2), не малы, так как по толщине пластины напряжения
. Хотя мы условились считать их малыми, но производные этих
напряжений, входящие в уравнения (1.2), не малы, так как по толщине пластины напряжения
![]() изменяются резко. Из
первых двух уравнений (1.2), пренебрегая проекциями объемных сил и интегрируя по z, получаем
изменяются резко. Из
первых двух уравнений (1.2), пренебрегая проекциями объемных сил и интегрируя по z, получаем
 .
.
Функции f1 и f2 находим из
граничных условий, составленных для нижней и верхней граней пластины: при ![]()
Тогда
 .
.
Из третьего уравнения (1.2) следует
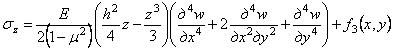 . (4.9)
. (4.9)
Нагрузка
интенсивностью q (x, у) приложена к верхней
грани пластины и направлена вниз, т. е. напряжение ![]() - сжимающее. Поэтому для определения функции f3 (x, у) можем написать граничные
условия:
- сжимающее. Поэтому для определения функции f3 (x, у) можем написать граничные
условия:
![]() (4.10)
(4.10)
Из первого условия найдем функцию f3 (x,y) и, подставив ее в (4.9), получим
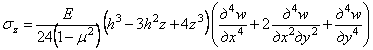 .
.
Подставив это выражение во второе условие (4.10), получим дифференциальное уравнение изогнутой срединной поверхности пластины
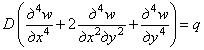 , (4.11)
, (4.11)
где
![]() (4.12)
(4.12)
- цилиндрическая жесткость пластины, аналогичная жесткости EJ балки, характеризующая способность пластины деформироваться. Размерность цилиндрической жесткости представляет собой произведение единицы силы на единицу длины. По величине D >EJ.
Уравнение (4.11) может быть сокращенно записано через оператор Лапласа:
![]()
Первый член, стоящий в скобках уравнения (4.11), учитывает прогиб, зависящий от изгиба в плоскости хz, третий член - в плоскости yz, а второй — прогиб, зависящий от кручения.
Решение уравнения (4.11) дает уравнение изогнутой срединной поверхности пластины
![]()
Если оно найдено, погонные изгибающие и крутящие моменты и поперечные силы, приходящиеся на единицу длины кромки пластины, определяют исходя из условий равновесия полосы пластины шириной, равной единице (рис. 50).
Составим
условие равновесия моментов относительно оси у и подставим в него
значение ![]() из формулы (4.6):
из формулы (4.6):
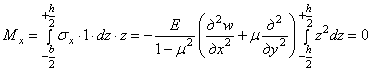 .
.
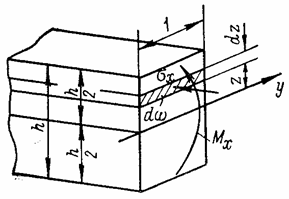
Рис. 50
Отсюда, с учетом формулы (4.12), для погонного изгибающего момента получим
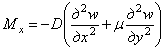 . (4.13)
. (4.13)
Аналогично из
условия ![]() найдем погонный
изгибающий момент
найдем погонный
изгибающий момент
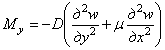 . (4.14)
. (4.14)
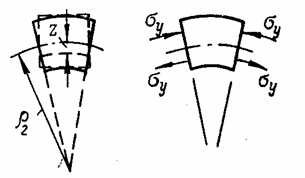
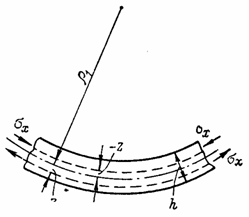
При действии одних только погонных изгибающих моментов Мх и Mу (рис. 51) пластина испытывает чистый изгиб в двух взаимно перпендикулярных
|
|
|
Рис. 51
направлениях. Срединная плоскость
ее превращается в изогнутую поверхность с главными радиусами кривизны ![]() (в сечении плоскостью,
параллельной плоскости х0z) и
(в сечении плоскостью,
параллельной плоскости х0z) и ![]() (в сечении плоскостью,
параллельной плоскости у0z). Соответствующие главные кривизны
срединной поверхности
(в сечении плоскостью,
параллельной плоскости у0z). Соответствующие главные кривизны
срединной поверхности
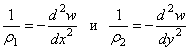 . (4.15)
. (4.15)
Составим,
учитывая (4.8), условия равенства крутящих моментов сумме моментов усилий,
возникающих от напряжений ![]() , и найдем погонные крутящие моменты:
, и найдем погонные крутящие моменты:
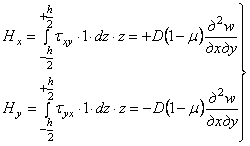 . (4.16)
. (4.16)
При действии одних только погонных крутящих моментов пластина испытывает чистое кручение.
Составим,
учитывая (4.8), условия равенства проекций поперечных сил сумме проекций
усилий, возникающих от напряжений ![]() (рис. 52).
(рис. 52).
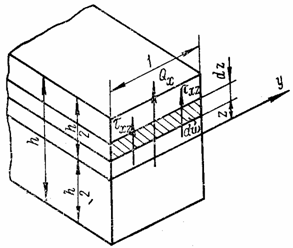
Рис. 52
Найдем погонные поперечные силы:
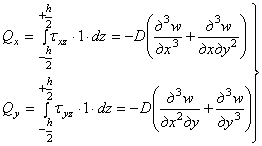 . (4.17)
. (4.17)
4.3 Цилиндрический и сферический изгиб пластины
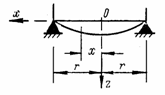
Цилиндрическим изгибом называется изгиб пластины по цилиндрической поверхности (рис. 53). Чтобы получить такой изгиб, закрепление двух параллельных кромок пластины должно обеспечивать неподвижность пластины, а две другие кромки должны быть свободны. Нагрузка должна иметь постоянную интенсивность в направлении, параллельном закрепленным кромкам (на рис. 53 параллельно оси у), а в перпендикулярном направлении может быть произвольной.
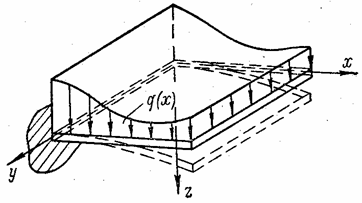
Рис. 53
На рис. 53
представлен цилиндрический поперечный изгиб под действием распределенной
нагрузки. Интенсивность нагрузки и реакция вдоль линии, параллельной закрепленной
кромке (оси у), постоянны, а кромки, параллельные оси х, свободны.
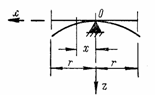
На рис. 54 показан цилиндрический чистый изгиб, который происходит под
действием моментов М1 и ![]() постоянной интенсивности,
распределенных по кромкам, параллельным оси у.
постоянной интенсивности,
распределенных по кромкам, параллельным оси у.
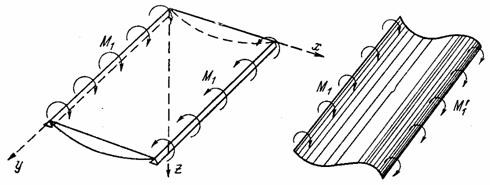
Рис. 54
Для
определения усилий, возникающих при чистом цилиндрическом изгибе,
рассматривается пластина, нагруженная по кромкам моментами М1
и ![]() (рис. 54). Размерность
изгибающего момента М1 приходящегося на единицу длины кромки,
т. е. погонного изгибающего момента,
(рис. 54). Размерность
изгибающего момента М1 приходящегося на единицу длины кромки,
т. е. погонного изгибающего момента,
![]()
Пластину нужно
представить себе рассеченной на ряд полос шириной, равной единице, сечениями,
параллельными оси х (рис. 55). Каждую из полос можно рассматривать как
балку, опертую своими концами и нагруженную по концам моментами М. Отличие
таких балок от полос пластины заключается в том, что у первых поперечные
деформации их сечений ничем не стеснены, тогда как поперечной деформации полосы
пластины (рис. 56) препятствуют соседние полосы, которые тоже стремятся
деформироваться в поперечном направлении.
Для полос, вырезанных на
некотором расстоянии от
кромок а,
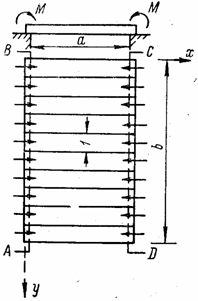
Рис. 55
можно считать, что относительная линейная деформация eу равна нулю, т. е. состояние пластины - плоское деформированное. При пользовании формулами подразд. 1.10 следует в соответствии с системой координат, принятой для пластин, заменить в них координату z на у, а координату у - на z.
|
|
|
Рис. 56
Дифференциальное уравнение изогнутой срединной поверхности и выражения для изгибающих моментов могут быть получены из соответствующих выражений подразд. 4.2, если учесть, что при цилиндрическом изгибе прогиб w не зависит от координат у и z. Тогда уравнение (4.11) примет вид
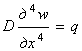 .
(4.18)
.
(4.18)
Проинтегрировав выражение (4.18) дважды, получим
![]() . (4.19)
. (4.19)
Уравнение (4.13) для погонного изгибающего момента примет вид
![]() .
(4.20)
.
(4.20)
Нормальное
напряжение, параллельное оси х,
![]() ,
(4.21)
,
(4.21)
где ![]() –
момент инерции полосы прямоугольного сечения шириной, равной единице.
–
момент инерции полосы прямоугольного сечения шириной, равной единице.
Так как на некотором расстоянии от свободных кромок пластина испытывает плоскую деформацию,
![]() .
.
Напряжение
![]() .
(4.22)
.
(4.22)
Выражение
(4.21) для ![]() ничем не отличается от
выражения для нормальных напряжений, возникающих в поперечном сечении балки
при ее чистом изгибе. Отличие цилиндрического изгиба пластины от изгиба балки
заключается в том, что в пластине, кроме напряжения
ничем не отличается от
выражения для нормальных напряжений, возникающих в поперечном сечении балки
при ее чистом изгибе. Отличие цилиндрического изгиба пластины от изгиба балки
заключается в том, что в пластине, кроме напряжения ![]() , возникает еще напряжение
, возникает еще напряжение ![]() . Прогибы w
пластины при цилиндрическом изгибе вычисляются путем двукратного последовательного
интегрирования дифференциального уравнения (4.19). Они оказываются меньше, чем
для балки-полосы, так как цилиндрическая жесткость D, стоящая в знаменателе правой
части уравнения (4.19), больше, чем жесткость балки EJ.
. Прогибы w
пластины при цилиндрическом изгибе вычисляются путем двукратного последовательного
интегрирования дифференциального уравнения (4.19). Они оказываются меньше, чем
для балки-полосы, так как цилиндрическая жесткость D, стоящая в знаменателе правой
части уравнения (4.19), больше, чем жесткость балки EJ.
Если пластина подвергается действию равномерно распределенных моментов по окружности (рис. 57), она изгибается по сферической поверхности.
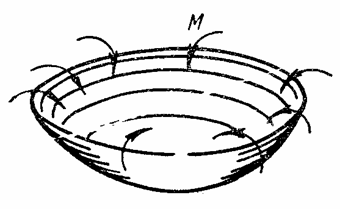
Рис. 57
Главные радиусы кривизны в любом сечении одинаковы:
![]() ,
,
поэтому на основании (4.15)
![]() .
(4.23)
.
(4.23)
Заменив вторые производные в уравнениях (4.13) и (4.14) кривизной, на основании формулы (4.23) получим изгибающий момент при сферическом изгибе
![]()
и выражение
для кривизны
![]() .
.
Дифференциальное уравнение (4.11) и выражения для крутящего и изгибающих моментов и для поперечных сил получены в предположении, что в срединной поверхности отсутствуют цепные погонные усилия: продольные Nх и Nу и сдвигающие Тху и Тух. Дифференциальные уравнения изгиба пластины конечной жесткости при наличии цепных усилий и выражения для усилий М, N, Q, Н и Т получены Карманом:
 .
(4.24)
.
(4.24)
Эта система может
быть сведена к системе двух совокупных дифференциальных уравнений с помощью
введения некоторой непрерывной функции ![]() , называемой функцией напряжений. Если выразить
продольные и сдвигающие силы N и Т через функцию напряжений
, называемой функцией напряжений. Если выразить
продольные и сдвигающие силы N и Т через функцию напряжений ![]()
![]() , (4.25)
, (4.25)
то можно
убедиться, что первые два уравнения системы (4.24) будут тождественно
удовлетворены при любом виде функции ![]() .
.
Подставив выражения (4.25) для цепных усилий N и Т во второе и третье уравнения системы (4.24) и заменив изгибающие и крутящие моменты М и Н их выражениями (4.13), (4.14), (4.16) получим следующую систему дифференциальных уравнений Кармана в частных производных:
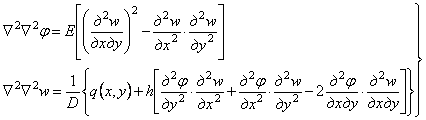 . (4.26)
. (4.26)
Уравнения
(4.26) применяют для расчета гибких пластин большого прогиба w > h/2. Если цепные усилия оказывают
малое влияние на изгиб, то в системе (4.26) следует пренебречь членами,
зависящими от ![]() . Первое уравнение системы (4.26) отпадает, а второе
принимает вид
. Первое уравнение системы (4.26) отпадает, а второе
принимает вид
![]() .
.
Этим уравнением мы и пользуемся для расчета плит и пластин средней толщины.
При расчете мембран, обладающих малой жесткостью на изгиб, в системе уравнений (4.26) следует пренебречь членами, пропорциональными цилиндрической жесткости. Тогда первое уравнение этой системы остается в силе, а второе уравнение примет вид
![]() .
.
В частном случае, когда сдвигающая сила Т равна нулю, продольные силы Nх = Nу = N и для определения w можно составить следующее дифференциальное уравнение:
![]() .
.
Решение дифференциального уравнения (4.11) в конечной форме получено для эллиптической и круглой пластин, защемленных на контуре и нагруженных равномерно распределенной нагрузкой. В остальных случаях пользуются приближенными решениями.
Интеграл
дифференциального уравнения (4.11), представляющего собой уравнение четвертой
степени в частных производных от двух независимых переменных, должен
удовлетворять восьми граничным условиям на контуре. На каждой кромке можно
составить по два условия, исходя из равенства нулю соответствующих двух
величин из числа следующих: прогиба w, угла ![]() , изгибающих моментов Мх или Mу, обобщенных
поперечных сил
, изгибающих моментов Мх или Mу, обобщенных
поперечных сил ![]() или
или ![]() .
.
Обобщенные поперечные силы представляют собой поперечные силы на свободных кромках пластины, заменяющие одновременное действие погонных крутящих моментов и поперечных сил
![]() .
.
Таким образом, общее число условий составляет 2 х 4 = 8. Например, для пластины (рис. 58) следует составить следующие восемь условий:
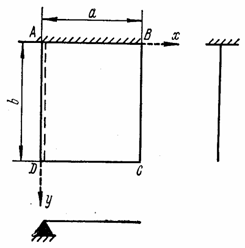
Рис. 58
-
кромка АВ
1)
при 0 < х <
а у = 0, w = 0;
2)
при 0 < х < а у = 0, ![]() = 0;
= 0;
- кромка AD
3)
при 0 < y < b x = 0, w = 0;
4)
при 0 < y < b x = 0, Мх = 0;
-
кромка DC
5)
при 0 < х <
а у = b, ![]() = 0;
= 0;
6)
при 0 < х <
а у = b, Му= 0;
- кромка ВС
7)
при 0 < у <
b у = a, ![]() = 0;
= 0;
8)
при 0 < х <
b у = а, Мх= 0;
Обычно
геометрические граничные условия, относящиеся к прогибам w и углам поворота сечений ![]() , выполняются точно, а статические граничные условия,
относящиеся к изгибающим моментам М и обобщенным поперечным силам Q0, - лишь в интегральной форме. После того
как будут найдены погонные изгибающие моменты, поперечные силы и крутящий
момент, напряжения можно определить по формулам сопротивления материалов
, выполняются точно, а статические граничные условия,
относящиеся к изгибающим моментам М и обобщенным поперечным силам Q0, - лишь в интегральной форме. После того
как будут найдены погонные изгибающие моменты, поперечные силы и крутящий
момент, напряжения можно определить по формулам сопротивления материалов
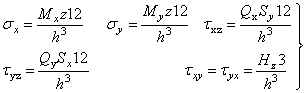 . (4.27)
. (4.27)
Наибольшие
нормальные напряжения от изгиба ![]() и
и ![]() и касательные напряжения
и касательные напряжения ![]() от кручения возникают
в точках верхней и нижней граней пластины. Наибольшие касательные напряжения
от кручения возникают
в точках верхней и нижней граней пластины. Наибольшие касательные напряжения ![]() и
и ![]() от перерезывания
возникают в срединной плоскости.
от перерезывания
возникают в срединной плоскости.
4.4 Изгибающие моменты при осесимметричном изгибе круглой пластины
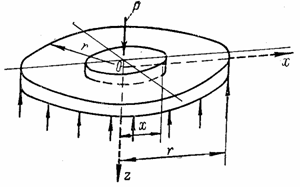
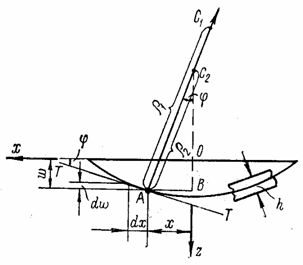
Если круглая пластина (рис. 59,а) подвергается действию нагрузки, симметричной относительно вертикальной оси z, проходящей через центр О пластины и называемой центральной осью, то изогнутая срединная поверхность ее представляет собой поверхность вращения, симметричную относительно оси z. Поэтому сечение пластины любой радиальной вертикальной плоскостью хОz, изображенное на рис. 59,б, окажется также симметричным относительно оси z. На рис.59 через х обозначена любая ось, лежащая в срединной плоскости и совпадающая с радиусом пластины; все точки А, лежащие на окружности радиусом х, испытывают одинаковое усилие, их вертикальные прогибы w (перемещения, параллельные оси z) тоже одинаковы.
|
а |
б |
|
|
|
Рис. 59
Если
координата х получила приращение dx, то прогиб w получит соответствующее приращение dw. Отношение
![]() (4.28)
(4.28)
представляет
собой приближенно, ввиду малости w, угол наклона, который составляет касательная ТТ,
проведенная в точке А, к изогнутой срединой поверхности пластины. При
заданном направлении оси z
тангенс угла ![]() и, следовательно, и
угол
и, следовательно, и
угол ![]() -
отрицательны. Как известно, криволинейная поверхность имеет в любой точке А
два главных радиуса кривизны
-
отрицательны. Как известно, криволинейная поверхность имеет в любой точке А
два главных радиуса кривизны ![]() и
и ![]() , из которых один наибольший, а другой наименьший. Радиусы
кривизны в данной точке совпадают с главной нормалью, т. е. с нормалью,
лежащей в плоскости кривизны и перпендикулярной к касательной плоскости,
проведенной в точке А к криволинейной поверхности.
, из которых один наибольший, а другой наименьший. Радиусы
кривизны в данной точке совпадают с главной нормалью, т. е. с нормалью,
лежащей в плоскости кривизны и перпендикулярной к касательной плоскости,
проведенной в точке А к криволинейной поверхности.
Для круглой
симметрично нагруженной пластины (рис. 60) главный радиус кривизны ![]() характеризует собой
кривизну изогнутой срединной поверхности в плоскости хОz. Центр C1 кривизны
может находиться выше или ниже плоскости Ох в зависимости от изгиба
пластины: выпуклостью вниз или вверх.
характеризует собой
кривизну изогнутой срединной поверхности в плоскости хОz. Центр C1 кривизны
может находиться выше или ниже плоскости Ох в зависимости от изгиба
пластины: выпуклостью вниз или вверх.
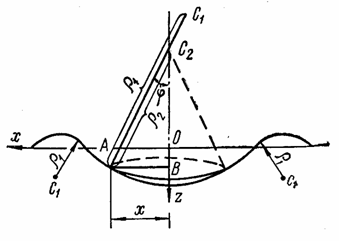
Рис. 60
Радиус
кривизны ![]() характеризует собой
кривизну изогнутой срединной поверхности в направлении, перпендикулярном к плоскости
чертежа, и представляет собой образующую конуса, вершина которого C2 лежит на
оси z, а радиус
основания равен х. На основании приближенного выражения аналитической
геометрии и зависимости (4.28) главная кривизна
характеризует собой
кривизну изогнутой срединной поверхности в направлении, перпендикулярном к плоскости
чертежа, и представляет собой образующую конуса, вершина которого C2 лежит на
оси z, а радиус
основания равен х. На основании приближенного выражения аналитической
геометрии и зависимости (4.28) главная кривизна
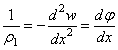 . (4.29)
. (4.29)
Из прямоугольного треугольника АВС2 видно, что
![]() ,
,
откуда вторая
главная кривизна
![]() . (4.30)
. (4.30)
Подстановка значений (4.29) и (4.30) в формулы (4.13), (4.14) с учетом (4.15) дает выражения для погонных изгибающих моментов радиального Мr и окружного МT :
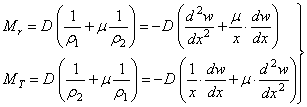 . (4.31)
. (4.31)
Для дальнейших выводов понадобится еще выражение производной погонного радиального изгибающего момента
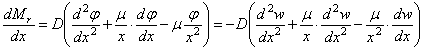 . (4.32)
. (4.32)
4.5 Дифференциальное уравнение изогнутой срединной поверхности круглой
пластины
Это уравнение
может быть получено из уравнения (4.11) путем преобразования его на основании
формул перехода от прямоугольных координат к полярным. Применительно к
осесимметричной задаче той же цели можно достигнуть при непосредственном рассмотрении
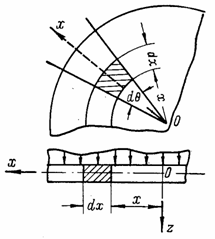
элемента круглой пластины. Для этого выделим из круглой пластины толщиной h, испытывающей
распределенную нагрузку, симметричную относительно центральной оси z, двумя радиальными
сечениями, составляющими между собой угол ![]() , и двумя окружными сечениями с радиусами х и х
+ dx элемент,
заштрихованный на рис. 61 и показанный
отдельно на рис. 62. Этот элемент подвергается действию не показанной на рис.
62 распределенной нагрузки, погонных поперечных сил Q и Q + dQ и погонных изгибающих радиальных
моментов Mr
и Мr
+ dMr
по окружным сечениям, а также погонных окружных изгибающих моментов МT по радиальным
сечениям.
, и двумя окружными сечениями с радиусами х и х
+ dx элемент,
заштрихованный на рис. 61 и показанный
отдельно на рис. 62. Этот элемент подвергается действию не показанной на рис.
62 распределенной нагрузки, погонных поперечных сил Q и Q + dQ и погонных изгибающих радиальных
моментов Mr
и Мr
+ dMr
по окружным сечениям, а также погонных окружных изгибающих моментов МT по радиальным
сечениям.
|
|
|
|
Рис. 61 |
Рис. 62 |
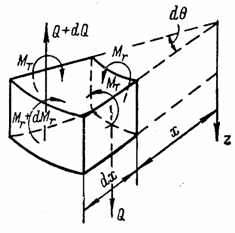
В силу симметрии нагрузки относительно центральной оси z поперечные силы по радиальным сечениям отсутствуют, а погонные изгибающие моменты МT одинаковы. На рис. 62 показаны изгибающие моменты, гнущие пластину выпуклостью вниз. Значения моментов приняты положительными.
Для составления уравнения равновесия элемента изгибающие моменты, действующие по граням элемента, изображаются в виде векторов (рис. 63). Стрелка вектора, перпендикулярного к плоскости действия момента, направлена в ту сторону, с которой вращение момента представляется происходящим по часовой стрелке. Приравняем нулю сумму проекций всех сил, действующих на вырезанный элемент, на ось Т, перпендикулярную к биссектрисе, делящей угол dq пополам.
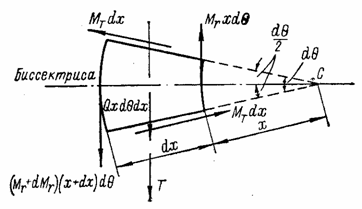
Рис. 63
При
составлении уравнения моментов можно пренебречь ввиду малости элемента
неравномерностью расположенной на нем нагрузки и моментом, вызванным
приращением dQ
поперечной силы в радиальном направлении. Поэтому поперечные силы, действующие
по граням элемента, сводятся к моменту с плечом dx, который изображается вектором ![]() , параллельным оси Т. Умножение всех погонных
усилий на длину грани, по которой они действуют, проектирование этих усилий на
ось Т и приравнивание суммы проекции нулю дает выражение
, параллельным оси Т. Умножение всех погонных
усилий на длину грани, по которой они действуют, проектирование этих усилий на
ось Т и приравнивание суммы проекции нулю дает выражение
![]() . (4.33)
. (4.33)
В уравнении
(4.33) синус угла ![]() ввиду малости заменен
углом
ввиду малости заменен
углом ![]() . После сокращения на
. После сокращения на ![]() , раскрытия скобок и отбрасывания члена dMr dx высшего
порядка малости уравнение (4.33) принимает вид
, раскрытия скобок и отбрасывания члена dMr dx высшего
порядка малости уравнение (4.33) принимает вид
![]()
или, после деления
всех членов на х dx,
![]() . (4.34)
. (4.34)
Подстановка в
уравнение (4.34) выражений для Мк, МТ и ![]() через
через ![]() по формулам (4.31) и
(4.32) приводит к уравнению
по формулам (4.31) и
(4.32) приводит к уравнению
![]() . (4.35)
. (4.35)
Уравнение
(4.35) представляет собой дифференциальное уравнение равновесия изогнутой
срединной поверхности круглой пластины, выраженное через угол ![]() , составляемый касательной к изогнутой срединной поверхности
с осью х.
, составляемый касательной к изогнутой срединной поверхности
с осью х.
Если в этом
уравнении на основании (4.28) заменить ![]() на
на ![]() , можно получить другой вид дифференциального
уравнения относительно вертикального перемещения w
, можно получить другой вид дифференциального
уравнения относительно вертикального перемещения w
![]() .
.
Погонная поперечная сила в круговом сечении радиусом х на основании рис. 64 при распределенной нагрузке
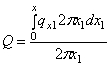 .
.
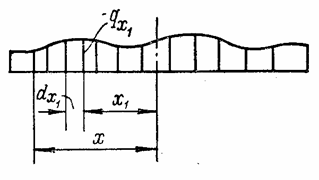
Рис. 64
Интегрируя
дифференциальное уравнение (4.35), можно найти уравнение углов ![]() , а затем, на основании зависимости (4.28), и уравнение
прогибов w в
виде функции от х. Произвольные постоянные, входящие в эти уравнения,
находятся из граничных условий на контуре пластины или на границе двух соседних
участков. При подстановке найденных выражений для
, а затем, на основании зависимости (4.28), и уравнение
прогибов w в
виде функции от х. Произвольные постоянные, входящие в эти уравнения,
находятся из граничных условий на контуре пластины или на границе двух соседних
участков. При подстановке найденных выражений для ![]() или w в
уравнения (4.31) находят выражения для радиального и окружного изгибающих моментов
в виде функции от х. По этим выражениям могут быть построены эпюры
изгибающих моментов и найдены их наибольшие значения.
или w в
уравнения (4.31) находят выражения для радиального и окружного изгибающих моментов
в виде функции от х. По этим выражениям могут быть построены эпюры
изгибающих моментов и найдены их наибольшие значения.
Пусть на круглую пластину (рис. 65) действуют направленные вниз равномерно распределенная нагрузка q и центральная сила Р. По наружному контуру радиусом r приложены произвольно направленные распределенные погонные силы Р0 и погонные изгибающие моменты М0 .
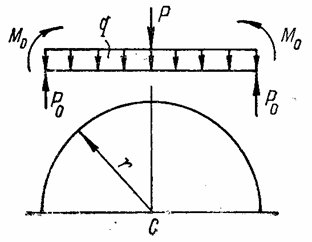
Рис. 65
Составим
уравнения углов ![]() и прогибов w. Для
возможности интегрирования левую часть уравнения (4.35) необходимо
преобразовать следующим образом:
и прогибов w. Для
возможности интегрирования левую часть уравнения (4.35) необходимо
преобразовать следующим образом:
![]() . (4.36)
. (4.36)
Приравняв суммарную поперечную силу по контуру радиусом х, равную Q2px (рис. 66), всей нагрузке, помещающейся на круге радиусом и равной Р + q×pх2, найдем погонную поперечную силу
![]() .
(4.37)
.
(4.37)
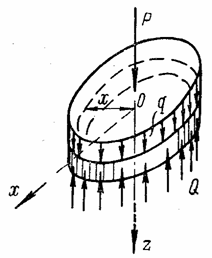
Рис. 66
Замена выражений, стоящих в левой и правой частях уравнения (4.35) соответствующими выражениями (4.36) и (4.37), приводит к легко интегрируемому дифференциальному уравнению
![]() . (4.38)
. (4.38)
Первое интегрирование выражения (4.38) дает
![]() .
(4.39)
.
(4.39)
Второе интегрирование выражения (4.39) дает
![]() . (4.40)
. (4.40)
Уравнение
(4.40) называется уравнением углов, составляемых касательной к изогнутой
срединной поверхности с осью х или уравнением углов поворота нормали к
изогнутой срединной поверхности. После подстановки в уравнение (4.40) вместо j
величины ![]() на основании формулы
(4.28) и умножения обеих частей уравнения на dx, оно получает вид
на основании формулы
(4.28) и умножения обеих частей уравнения на dx, оно получает вид
![]() .
.
Интегрирование дает
![]() . (4.41)
. (4.41)
Уравнение
(4.41) называется уравнением прогибов или уравнением изогнутой срединной
поверхности пластины.
4.6 Граничные условия. Наибольшие напряжения и прогибы.
Условия прочности
Так как число произвольных постоянных в уравнении (4.41) равно трем, то для нахождения постоянных С следует составить следующие три граничные условия:
|
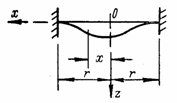
- для защемленной кромки пластины (рис. 67,а) 1)
х = r, w = 0;
2) x =
r, |
а |
|
|
|
|
- для свободно опертой кромки пластины (рис. 67, б) 1)
х = r, w = 0;
2) x =
r, Mr = 0; 3) x = 0, |
б |
|
|
|
|
- для свободной кромки (рис. 67,в) 1)
х = r, Mr = 0; 2) x = r,
|
в |
|
|
|
|
|
Рис. 67 |
Дифференциальное уравнение (4.38) и его интегралы, а также выражения (4.31) справедливы и для кольцевой пластины в виде круглой пластины с круглым отверстием в середине (рис. 68,а) или в виде кольцевой пластины,
|
а |
б |
в |
|
|
|
|
Рис. 68
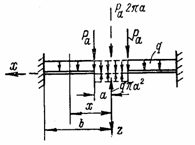
внутренний контур которой защемлен (рис. 68,б). Изменяются лишь граничные условия и для центральной силы Р должно быть составлено выражение, отражающее изменение поперечной силы в сечении х [см. формулу (4.37)].
Например, для пластины, изображенной на рис.
68, а, граничное условие х =
0, w =
0 теряет смысл, так как при х = 0 нет пластины. Поэтому следует
воспользоваться следующими тремя условиями: 1) х = b; w = 0; 2) х = b, ![]() = 0; 3) x = a, Mr = 0. Для сосредоточенной силы получится
выражение
= 0; 3) x = a, Mr = 0. Для сосредоточенной силы получится
выражение
![]() .
.
В этом выражении первый член представляет собой приложенную в центре и направленную вниз равнодействующую погонных сил Pa, приложенных к контуру радиусом а (сила Р на рис. 65), а второй член - силу, приложенную в центре и направленную вверх, компенсирующую ту распределенную нагрузку, которой надо заполнить круг радиусом а, чтобы привести схему, изображенную на рис, к схеме, показанной на рис. 68,а. При такой замене уравнения остаются в силе и при наличии отверстия, так как координаты х всегда больше а и изменение расчетной схемы при х < а на вывод этих уравнений не влияет.
Для пластины, изображенной на рис. 68,б, следует воспользоваться следующими граничными условиями:
1)
х = а, w = 0; 2) х = а, ![]() = 0; 3) х
= b, Mr = 0. Для
сосредоточенной силы получится выражение
= 0; 3) х
= b, Mr = 0. Для
сосредоточенной силы получится выражение
![]() .
.
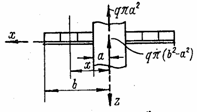
Если, в частном случае, одна из нагрузок q или Р отсутствует, то в формулах (4.40) и (4.41) ее следует положить равной нулю. Например, для пластины, показанной на рис. 68,в, выражение для прогиба будет
![]() .
.
Если для отдельных участков пластины выражения поперечной силы различны (рис. 69), то для каждого из участков должно быть составлено свое дифференциальное уравнение. Например, для суммарной поперечной силы на первом участке пластины
![]() ,
,
на втором участке
![]() .
.
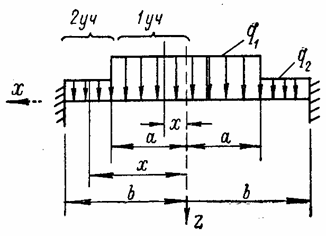
Рис. 69
После
интегрирования каждого дифференциального уравнения получится три произвольных
постоянных и общее число произвольных постоянных окажется равным 3п (п - число
участков). Для каждой границы между двумя соседними участками могут быть
составлены три дополнительных условия, выражающих то обстоятельство, что на
границе двух соседних участков прогиб w, угол j и радиальный момент Мr одинаковы: 1) х =
a, w1 = w2, 2) х = a, ![]() ; 3) х = а, (Мr)1= (Мr)2.
Таких дополнительных условий оказывается как раз столько, сколько недостает
для нахождения всех произвольных постоянных. В разобранном примере при двух
участках число произвольных постоянных 2 ´ 3 = 6, число
условий 3 + 3 = 6.
; 3) х = а, (Мr)1= (Мr)2.
Таких дополнительных условий оказывается как раз столько, сколько недостает
для нахождения всех произвольных постоянных. В разобранном примере при двух
участках число произвольных постоянных 2 ´ 3 = 6, число
условий 3 + 3 = 6.
Если известны выражения для изгибающих моментов Мr и МT и прогибов w в функции от х, то координаты х, соответствующие наибольшим значениям этих величин, найдутся из условий
![]() .
(4.42)
.
(4.42)
В ряде случаев сечения, в которых возникают наибольшие изгибающие моменты или прогибы, известны. Например, в схеме на рис. 68,б наибольший прогиб возникает на наружном контуре при х = b, а наибольший радиальный изгибающий момент (Mr)max - в защемлении при х = а.
Подставив найденные из условий (4.42) значения х в выражения для изгибающих моментов, можно получить значения (Mr)max и (МТ)max которые, в общем случае, могут возникнуть в разных сечениях пластины. Опасное сечение может оказаться поэтому там, где погонные изгибающие моменты Мr и MT одновременно велики.
Главные напряжения на наружной и внутренней поверхностях пластины в опасном сечении вычисляются по формулам, аналогичным (4.27), путем замены момента инерции на момент сопротивления:
![]() .
.
Третье главное
напряжение (по площадке, параллельной срединной плоскости) равно нулю.
Расчетное напряжение, сравниваемое с допускаемым, вычисляется в зависимости от
знаков напряжений ![]() и
и ![]() по одной из теорий
прочности. Например, для пластины, представленной на рис. 68,б, опасное
сечение находится в защемлении при х = а; при этом верхние
волокна и от момента Мr, и от момента МT испытывают растяжение, а
нижние -
сжатие, изгибающий момент Мr в сечении х = а больше, чем МT. Предполагаем, что
пластина выполнена из пластического материала и что применяется третья теория
прочности, условие прочности по которой
по одной из теорий
прочности. Например, для пластины, представленной на рис. 68,б, опасное
сечение находится в защемлении при х = а; при этом верхние
волокна и от момента Мr, и от момента МT испытывают растяжение, а
нижние -
сжатие, изгибающий момент Мr в сечении х = а больше, чем МT. Предполагаем, что
пластина выполнена из пластического материала и что применяется третья теория
прочности, условие прочности по которой
![]() .
.
Волокна в
точке на верхней поверхности пластины растянуты, т. е. напряжения ![]() положительны, поэтому
следует обозначить:
положительны, поэтому
следует обозначить:
![]() .
.
Условие прочности примет вид
![]() .
.
4.7 Температурные напряжения в пластинах
В общем случае
температура в какой-либо точке круглой пластины является функцией двух
переменных: радиуса х и расстояния z от точки до срединной плоскости. В
силу линейности основных уравнений для температурных напряжений напряжения,
вызванные радиальным изменением
температуры -
tx2
– tx1
и изменением температуры по толщине t2 – t1 можно вычислить отдельно, а затем
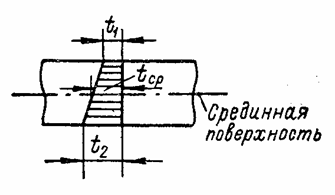
алгебраически суммировать. Ниже рассматриваются два случая изменения
температуры: 1) температура одинакова для всех точек, расположенных на
одинаковом расстоянии z от срединной плоскости, но меняется по толщине
пластины по прямолинейному закону; 2) температура постоянна по толщине, не
зависит от полярного угла ![]() , но меняется в зависимости от расстояния х между
точкой и центром пластины.
, но меняется в зависимости от расстояния х между
точкой и центром пластины.
Случай 1.
При одинаковом во всех точках одной окружности изменении температуры по толщине
пластины ![]() , подчиняющемся прямолинейному закону (рис. 70), перемещение
этих точек пластины, связанное с ее расширением или сжатием, происходит также
одинаково по всем направлениям в плане.
, подчиняющемся прямолинейному закону (рис. 70), перемещение
этих точек пластины, связанное с ее расширением или сжатием, происходит также
одинаково по всем направлениям в плане.
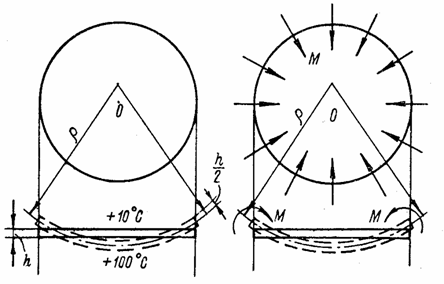
В случае повышения температуры верхняя поверхность пластины получает большее расширение, чем нижняя, и пластина изгибается по шаровой поверхности радиусом r выпуклостью вверх. На основании допущения о прямых нормалях можно считать, что относительная деформация (по отношению к срединному слою), происходящая на наружной поверхности в любом направлении,
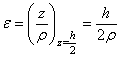 . (4.43)
. (4.43)
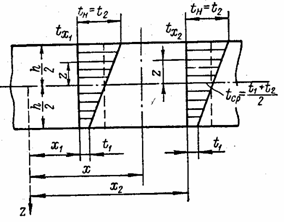
Рис. 70
С другой стороны, относительная температурная деформация отрезка длиной l на наружной поверхности по отношению к срединному слою
![]() . (4.44)
. (4.44)
Приравняв выражения (4.43) и (4.44), можно получить формулу для определения кривизны шаровой изогнутой поверхности
![]() .
(4.45)
.
(4.45)
Если круглая пластина не имеет закреплений или свободно поворачивается на контуре (свободно оперта), то температурное искривление не вызывает дополнительных усилий. Если же пластина защемлена, на контуре возникнут погонные опорные моменты Мr, уничтожающие кривизну, вызванную неравномерным нагревом.
При сферическом изгибе моментами Мr кривизна
![]() . (4.46)
. (4.46)
Приравняв выражения (4.45) и (4.46), получим формулу для определения погонного изгибающего момента
![]() ,
,
а разделив это
выражение на момент сопротивления ![]() и подставив вместо
цилиндрической жесткости D
ее значение из формулы (4.12), определим наибольшее напряжение:
и подставив вместо
цилиндрической жесткости D
ее значение из формулы (4.12), определим наибольшее напряжение:
![]() . (4.47)
. (4.47)
Случай 2. Круглая пластина с центральным отверстием радиусом а подвергается действию температуры, имеющей радиальный перепад (рис. 71).
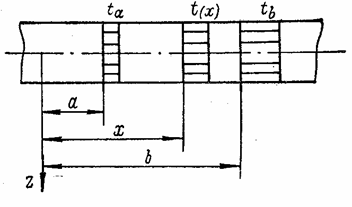
Рис. 71
В дальнейшем t(x) обозначено для
краткости t.
Напряженное состояние в пластине считаем плоским, т. е. полагаем ![]() = 0. В силу симметрии условий и расчетной
схемы перемещения и зависят только от радиуса х, а перемещения v равны нулю. Поэтому
относительные деформации
= 0. В силу симметрии условий и расчетной
схемы перемещения и зависят только от радиуса х, а перемещения v равны нулю. Поэтому
относительные деформации
 . (4.48)
. (4.48)
Если решить
первые два уравнения (4.48) относительно ![]() и
и ![]() ,
а в третьем заменить
,
а в третьем заменить ![]() на
на ![]() , можно получить
, можно получить
 . (4.49)
. (4.49)
Подстановка
значений (4.49) в уравнение равновесия ![]() плоской задачи в
полярных координатах, принимающее в данном случае (
плоской задачи в
полярных координатах, принимающее в данном случае (![]() ) вид
) вид
![]() ,
,
приводит к следующему дифференциальному уравнению для радиального перемещения:
![]() .
.
Для интегрирования этого уравнения левая его часть записывается так [см. аналогичное решение уравнения (4.36)]:
![]() . (4.50)
. (4.50)
Первое и второе интегрирование (4.50) дает
![]() . (4.51)
. (4.51)
В выражении (4.51) через х1 обозначен переменный радиус, определяющий точки, расположенные между а и х. Если подставить это выражение в формулы (4.49), то получатся следующие выражения для температурных напряжений:
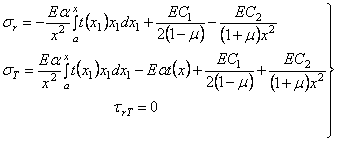 . (4.52)
. (4.52)
Постоянные С1
и С2 определяются из граничных условий на контурах пластины.
Если отверстия радиусом а в пластине нет, то интегрирование в
формулах (4.52) выполняется в пределах от нуля до х.
4.8 Определение усилий в мембранах. Цепные усилия и напряжения
Мембрана обладает малой жесткостью на изгиб и поэтому обычно рассчитывается лишь на действие цепных продольных усилий Nх и Nу в срединной плоскости и на вызываемые ими равномерно распределенные по толщине напряжения. Прогибы w мембраны составляют обычно не менее пяти толщин h и в большую сторону не ограничиваются.
Реактивные усилия S на закрепленном контуре (рис. 72) направлены по касательной к изогнутой срединной поверхности мембраны. Они могут быть разложены на составляющие: вертикальную Sz и горизонтальную Sx. Наличие горизонтальной составляющей реактивного усилия (распора), возникающей при действии вертикальной нагрузки, - особенность мембраны по сравнению с пластиной средней толщины и плитой.
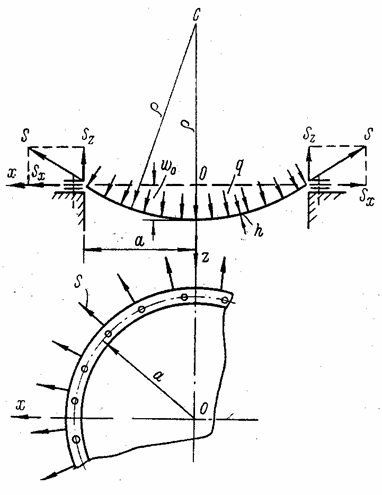
Рис. 72
Дифференциальные
уравнения изогнутой поверхности мембраны получаются из дифференциальных
уравнений (4.26) для пластины, у которой прогиб превышает половину толщины,
если положить в них цилиндрическую жесткость D равной нулю. Так как в выражении
цилиндрической жесткости модуль упругости Е нулю не равен, она будет
равна нулю, если дробь ![]() можно считать
пренебрежимо малой.
можно считать
пренебрежимо малой.
Функцию
прогибов w и
функцию напряжений ![]() в мембране можно найти
из системы двух уравнений
в мембране можно найти
из системы двух уравнений
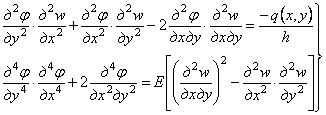 . (4.53)
. (4.53)
Уравнения
(4.53) решаются приближенно. Если функция ![]() найдена, выражения для
растягивающих цепных усилий Nx и Ny в мембране могут быть
вычислены по формулам
найдена, выражения для
растягивающих цепных усилий Nx и Ny в мембране могут быть
вычислены по формулам
![]() , (4.54)
, (4.54)
а соответствующие цепные напряжения найдены из выражений
![]() .
.
Изгибающие и крутящие моменты, а также перерезывающие силы и соответствующие им напряжения в мембране отсутствуют.
4.9 Приближенное определение прогиба и напряжений в круглой мембране
При выводе
приближенных формул предполагается, что защемленная на контуре мембрана
радиусом а и толщиной h (рис.72) изгибается, образуя шаровую поверхность, и что
нагрузка q действует
по нормали к этой изогнутой поверхности.
При этих условиях
усилия N и
напряжение ![]() (рис. 73,а)
(рис. 73,а)
|
а |
б |
|
|
|
Рис. 73
по кромкам элемента, вырезанного из мембраны двумя взаимно перпендикулярными сечениями, окажутся одинаковыми. При размерах элемента, равных единице,
![]() .
(4.55)
.
(4.55)
Согласно уравнению равновесия сумма проекций нагрузки и усилий, действующих по кромкам элемента на нормаль z к поверхности элемента
![]() (4.56)
(4.56)
Центральный
угол ![]() выражаем через длину дуги
кромки элемента и радиус кривизны
выражаем через длину дуги
кромки элемента и радиус кривизны ![]() . Замена в уравнении (4.56), ввиду малости
. Замена в уравнении (4.56), ввиду малости ![]() ,
,
![]()
дает выражение:
- для усилия ![]() ;
;
- для кривизны ![]() . (4.57)
. (4.57)
Тогда для напряжения из формулы (4.55) получим
![]() . (4.58)
. (4.58)
Приближенное дифференциальное уравнение изогнутой срединной поверхности на основании зависимости (4.57)
![]() .
.
Величина прогиба в середине мембраны получается на основании закона сохранения энергии
U = A. (4.59)
где U – потенциальная энергия деформации мембраны;
A – работа внешних сил на перемещениях, вызванных деформацией мембраны.
Потенциальная энергия мембраны
![]() ,
(4.60)
,
(4.60)
где удельная потенциальная энергия деформации с учетом того, что на основании закона Гука
![]() ,
,
может быть выражена через напряжение следующим образом:
![]() .
.
Тогда, на основании формулы, (4.58)
![]() . (4.61)
. (4.61)
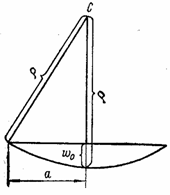
Зависимость
между радиусом кривизны ![]() и прогибом w0 в середине мембраны (рис. 73,б)
и прогибом w0 в середине мембраны (рис. 73,б)
![]()
или после
возведения скобки в квадрат и отбрасывания ![]() как величины высшего
порядка малости
как величины высшего
порядка малости
![]()
откуда
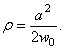 (4.62)
(4.62)
Подстановка
этого значения ![]() в формулу (4.61) и
значения и в формулу (4.60) дает выражение для потенциальной энергии
в формулу (4.61) и
значения и в формулу (4.60) дает выражение для потенциальной энергии
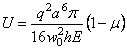 . (4.63)
. (4.63)
Работа А
внешних сил получится как интеграл, взятый по площади мембраны, половины произведения элементарной
силы qdxdy на
прогиб w (ху):
![]() (4.64)
(4.64)
Интеграл в выражении (4.64) представляет собой объем Vш.с. шарового сегмента с высотой w0 и радиусом а:
![]()
или, если
отбросить ![]() ,
,
![]() .
.
Поэтому выражение (4.64) примет вид
![]() .
(4.65)
.
(4.65)
При подстановке значений (4.63) и (4.65) в выражение (4.59), получаем
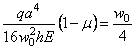 .
.
Тогда прогиб в середине мембраны
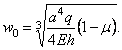
Для стальной
мембраны при ![]() = 0,3 прогиб
= 0,3 прогиб
![]() .
(4.66)
.
(4.66)
Точное решение, полученное путем интегрирования дифференциальных уравнений (4.53), дает
![]() .
.
Нормальное
напряжение ![]() получается, если в
формулу (4.58) подставить r из формулы (4.62) и w0 из формулы (4.66):
получается, если в
формулу (4.58) подставить r из формулы (4.62) и w0 из формулы (4.66):
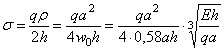
или
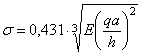 .
.
Точное решение на базе системы (4.53) дает выражение
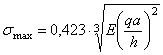 .
.
4.10 Примеры
Пример 4.1.
Определить нормальные напряжения ![]() и
и ![]() в точке на верхней
поверхности прямоугольной пластины, испытывающей изгиб от моментов М = 0,014
Мнм, распределенных по кромках AD и ВС (рис. 74).
Определить радиус кривизны
в точке на верхней
поверхности прямоугольной пластины, испытывающей изгиб от моментов М = 0,014
Мнм, распределенных по кромках AD и ВС (рис. 74).
Определить радиус кривизны ![]() изогнутой срединной
поверхности и наибольший прогиб w. Е = 2
изогнутой срединной
поверхности и наибольший прогиб w. Е = 2![]() Мн/м2;
Мн/м2; ![]() = 0,27.
= 0,27.
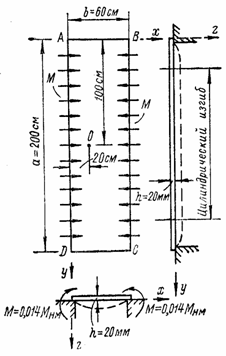
Рис. 74
Решение.
Отношение
сторон пластины ![]() Следовательно,
напряжения в средней части пролета можно вычислить по формулам цилиндрического
изгиба.
Следовательно,
напряжения в средней части пролета можно вычислить по формулам цилиндрического
изгиба.
Погонный
изгибающий момент по кромкам AD и ВС
![]() .
.
Напряжения по формулам (4.21) и (4.22)
![]()
![]()
Такие же напряжения будут во всех точках верхней поверхности в пределах цилиндрического изгиба.
Цилиндрическая жесткость
![]()
Кривизна срединной поверхности по формулам (4.15) и (4.19)
![]()
поэтому дифференциальное уравнение изогнутой срединной поверхности
![]()
или
![]()
Два последовательных интегрирования дифференциального уравнения дают
![]()
![]() (4.67)
(4.67)
Условия для
определения произвольных постоянных: 1) х
= 0, w = 0 (прогиб по кромке AD отсутствует); 2) х =
0,30 м, ![]() (касательная к изогнутой
срединной поверхности в середине пролета горизонтальна). Из первого условия
следует, что С2 = 0. Из
второго условия
(касательная к изогнутой
срединной поверхности в середине пролета горизонтальна). Из первого условия
следует, что С2 = 0. Из
второго условия ![]() откуда
откуда
![]()
Подставляя
найденные значения С1 и С2 в уравнение
прогибов (4.67), получаем ![]()
Наибольший прогиб при х = 0,30 м
![]() .
.
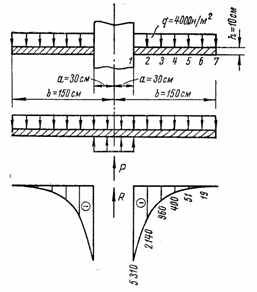
Пример 4.2.
Для заданной схемы круглой пластины (рис. 75,а) построить эпюру погонных
радиальных изгибающих моментов. Коэффициент поперечной деформации m
= 0,13; модуль продольной упругости Е = 2![]() н/см2.
н/см2.
|
а б в |
|
Рис. 75
Решение.
Заданная схема
отличается от схемы, для которой выведены формулы (4.40) и (4.41), тем, что на
окружности радиусом а = 30 см
нет равномерно распределенной нагрузки. Если эту нагрузку приложить, то для
сохранения заданных условий нужно уравновесить ее аналогичной нагрузкой, приложенной
снизу (рис. 75,б), которую можно заменить равнодействующей сосредоточенной
силой ![]() на оси симметрии
пластины. Кроме того, на этой оси действует реакция R, равная весу нагрузки, лежащей на
пластине,
на оси симметрии
пластины. Кроме того, на этой оси действует реакция R, равная весу нагрузки, лежащей на
пластине,
![]() .
.
Полная сосредоточенная сила на оси пластины
![]() (4.68)
(4.68)
Знак минус введен потому, что сила Р направлена снизу вверх.
Таким образом,
выражения (4.40) и (4.41) для ![]() и w могут быть использованы для схемы
на рис. 75,а, если вместо Р подставить в них выражение (4.68).
Интенсивность нагрузки q
= 4000 н/м2 =
0,4 н/см2.
и w могут быть использованы для схемы
на рис. 75,а, если вместо Р подставить в них выражение (4.68).
Интенсивность нагрузки q
= 4000 н/м2 =
0,4 н/см2.
Уравнение углов поворота
![]() .
.
В формулу (4.31) для радиального момента входит
![]() ,
,
![]()
При подстановке этих выражения в формулу (4.31) получаем

Цилиндрическая жесткость
![]() .
.
Так как
![]()
то получим
![]()
Момент
![]()
угол
![]()
Условия для определения произвольных постоянных: 1) х = а, j = 0; 2) х = b, Mr = 0. Из первого условия
![]()
После выполнения арифметических действий
![]()
Из второго условия
![]()
После выполнения арифметических действий
![]()
Совместное решение уравнения (4.69) и (4.70) дает значения произвольных постоянных:
![]()
Подставив значения D и найденные значения произвольных постоянных в выражение для изгибающего момента Mr, получим
![]()
Подставляя последовательно значения х через 20 см в это уравнение, можно найти значения радиальных моментов (табл. 3). По этим ординатам построена эпюра радиальных моментов (рис. 75,в).
Таблица 3
|
Номер точки |
х |
х2 |
lnx |
6,342(2,26lnx+0,87) |
0,00046x2 |
|
Mr нсм/см |
|
1 |
30 |
900 |
3,401 |
54,2 |
0,414 |
18,853 |
-5310 |
|
2 |
50 |
2500 |
3,912 |
61,5 |
1,150 |
6,787 |
-2140 |
|
3 |
70 |
4900 |
4,248 |
66,3 |
2,254 |
3,463 |
-960 |
|
4 |
90 |
8100 |
4,500 |
69,7 |
3,726 |
2,094 |
-400 |
|
5 |
110 |
12100 |
4,700 |
72,9 |
5,566 |
1,402 |
-51 |
|
6 |
130 |
16900 |
4,847 |
74,9 |
7,774 |
1,004 |
-19 |
|
7 |
150 |
22500 |
5,011 |
77,3 |
10,350 |
0,754 |
0 |
Пример 4.3.
Определить радиус кривизны ![]() изогнутой срединной
поверхности круглой пластины толщиной h = 20 мм
(рис. 76,а), если температура t2 на ее нижней поверхности изменилась от нуля до
+100 °С, а температура t1 на верхней поверхности - от нуля до +10 °С.
изогнутой срединной
поверхности круглой пластины толщиной h = 20 мм
(рис. 76,а), если температура t2 на ее нижней поверхности изменилась от нуля до
+100 °С, а температура t1 на верхней поверхности - от нуля до +10 °С.
Определить
наибольший изгибающий момент и напряжения, которые возникнут в пластине. Коэффициент
линейного температурного расширения ![]() = 0,000012; Е = 2
= 0,000012; Е = 2 ![]() Мн/м2;
Мн/м2; ![]() = 0,28.
= 0,28.
|
а |
б |
|
|
|
|
в |
|
|
|
|
Рис. 76
Решение.
Изменение температуры по толщине пластины (рис. 76,в)
![]() .
.
Относительная температурная деформация нижнего или верхнего волокна по формуле (4.44)
![]()
Кривизна изогнутой срединной поверхности по формуле (4.45)
![]()
Радиус кривизны
![]()
Напряжения, возникающие в пластине при изменении температуры, равны напряжениям, которые возникнут, если приложить по контуру пластины радиальные изгибающие моменты (рис. 76,б), вычисляемые по формуле (4.46),
![]() .
.
Напряжение на поверхности
![]()
Ту же величину
напряжения ![]() можно получить по
формуле (4.47).
можно получить по
формуле (4.47).
Пример 4.4. Составить выражение для температурных напряжений в сплошной круглой свободной на контуре пластине, температура которой падает от центра к наружному контуру по квадратичному закону
![]()
Определить
наибольшее окружное нормальное напряжение при следующих данных: Е= 2![]() Мн/м2,
температура в центре t0=
+100 °С, на наружном контуре (х = b) tb, = +20 °С.
Мн/м2,
температура в центре t0=
+100 °С, на наружном контуре (х = b) tb, = +20 °С.
Решение.
Граничные условия: 1) х = 0, t = t0; 2) х = b, t = tb. Условия для определения произвольных постоянных С1 и С2 следующие.
1. Перемещение и в центре пластины равно нулю. Следовательно, при х = 0 и = 0 и из формулы (4.51) С2 = 0.
2. На наружном
контуре радиальный момент Mr
= 0, и, следовательно, радиальные напряжения
![]() отсутствуют. Поэтому
при х = b,
отсутствуют. Поэтому
при х = b, ![]() = 0 и из формулы (4.52)
= 0 и из формулы (4.52)
![]()
Если учесть в этом выражении заданный закон изменения температуры и произвести интегрирование, то
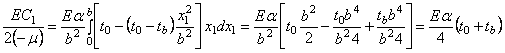 .
.
Поэтому по формулам (4.52) получаются следующие выражения для напряжений:
![]()
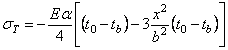 .
.
или, в окончательном виде,
 . (4.71)
. (4.71)
На основании
уравнений (4.71) можно заключить, что напряжения ![]() во всех точках
сжимающие (отрицательные), так как выражение в скобках (t0 – tb) положительно,
а
во всех точках
сжимающие (отрицательные), так как выражение в скобках (t0 – tb) положительно,
а ![]() . Напряжение же
. Напряжение же ![]() может быть и
положительным. Это наибольшее (положительное) напряжение
может быть и
положительным. Это наибольшее (положительное) напряжение ![]() получится при
наибольшем отрицательном значении
получится при
наибольшем отрицательном значении 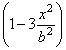 при х = b :
при х = b :
![]()
Пример 4.5. Определить радиальный и окружной изгибающие моменты и, пользуясь третьей теорией прочности, расчетные напряжения на нижней поверхности в центре круглой стальной крышки, опертой по контуру и нагруженной равномерно распределенной внешней нагрузкой (рис. 77).
Определить величину прогиба в центре крышки.
Наружный радиус пластины r
=200 мм, толщина h =10 мм; интенсивность равномерно
распределенной нагрузки q
=12 н/см2; E =2![]() н/см2;
н/см2; ![]() = 0,3.
= 0,3.
Решение.
По формулам
(4.40) и (4.41), полагая в них Р = 0, находим уравнения углов ![]() и прогибов w :
и прогибов w :
![]() (4.72)
(4.72)
![]() .
.
Граничные
условия для пластины с опертыми краями: 1) х = 0, ![]() = 0; 2) х = r, w = 0; 3) х = r, Mr = 0. Из первого условия находим
= 0; 2) х = r, w = 0; 3) х = r, Mr = 0. Из первого условия находим ![]() или С2= 0. Из второго условия получаем
уравнение с двумя неизвестными C1 и С3
или С2= 0. Из второго условия получаем
уравнение с двумя неизвестными C1 и С3
![]() . (4.73)
. (4.73)
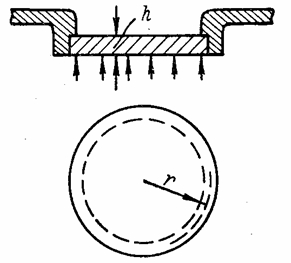
Рис. 77
Для использования третьего условия составим выражение радиального изгибающего момента [см. формулу (4.31)]
![]() .
(4.74)
.
(4.74)
Дифференцируя (4.72) и учитывая, что C2 = 0, находим
![]() .
.
Подставляя это выражение и выражение (4.72) в формулу (4.74), получаем
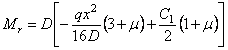 .
.
На основании третьего условия
![]()
Отсюда произвольная постоянная
![]() .
.
Подставляя это значение C1 в уравнение (4.73), получаем произвольную постоянную
![]() .
.
При найденных произвольных постоянных выражение для радиального изгибающего момента примет вид:
![]() . (4.75)
. (4.75)
Окружной изгибающий момент [см. формулу (4.31)] выразится так:
 (4.76)
(4.76)
Из выражений (4.75) и (4.76) видно, что наибольшие значения радиального и окружного изгибающих моментов Mr и MT получаются при х = 0, т. е. в центре пластины.
![]() .
.
Соответствующие напряжения на нижней поверхности пластины растягивающие:
![]() .
.
Главные напряжения
![]() 5940 н/см2,
5940 н/см2,
![]() = 0, поэтому, на основании третьей теории прочности,
расчетное напряжение
= 0, поэтому, на основании третьей теории прочности,
расчетное напряжение
![]() .
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов