Главная
Лекция 3. Толстостенные трубы
3.1 Общие сведения. Уравнение равновесия элемента трубы
Если толщина стенки трубы, нагруженной радиальной нагрузкой, превышает 0,1 радиуса геометрической оси стенки, труба считается толстостенной. Распределение напряжений по толщине стенки такой трубы нельзя считать равномерным; радиальные перемещения отдельных точек стенки трубы зависят от их расстояния r до оси трубы.
С помощью теории расчета толстостенных труб определяются напряжения и перемещения в точках стенок цилиндров машин, стволов орудий, при температурных или прессовых посадках рубашек, муфт и ступиц на валы, а также в облицовках тоннелей и стволов, подверженных горному давлению.
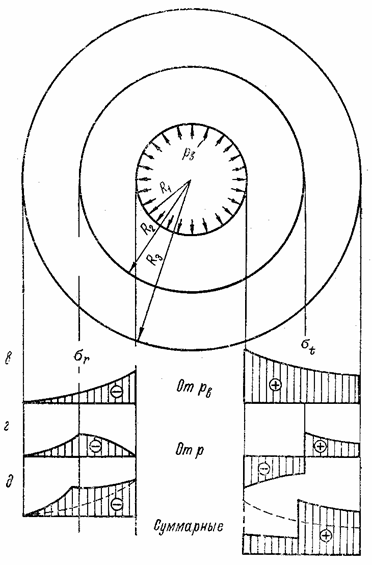
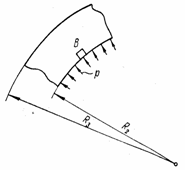
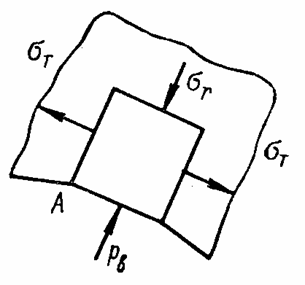
Рассмотрим отрезок трубы длиной, равной единице, вырезанный двумя сечениями, нормальными к оси трубы (рис. 30,а). Труба нагружена на внутренней и наружной поверхностях радиальной сжимающей нагрузкой; интенсивности рВ и рН этой нагрузки постоянны как вдоль оси трубы, так и по ее окружности. Любой такой отрезок на некотором расстоянии от торцов трубы находится в плоском деформированном состоянии.
а
б
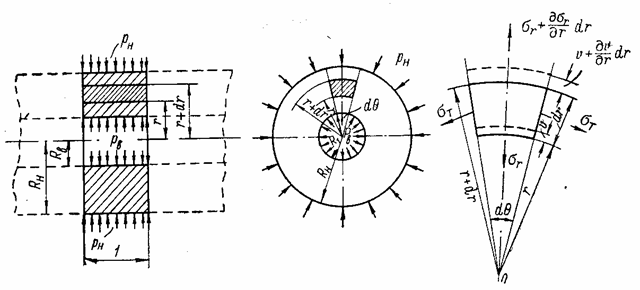
Рис. 30
Составим уравнение равновесия
элемента трубы, выделенного двумя радиальными сечениями, составляющими между
собой угол ![]() , и двумя окружными сечениями, радиусы которых r и r + dr (рис. 30,б).
По граням этого элемента действуют радиальные и окружные напряжения
, и двумя окружными сечениями, радиусы которых r и r + dr (рис. 30,б).
По граням этого элемента действуют радиальные и окружные напряжения ![]() и
и ![]() . Радиальное напряжение при изменении радиуса r получает приращение
. Радиальное напряжение при изменении радиуса r получает приращение ![]() , а окружное напряжение
, а окружное напряжение ![]() в силу осевой
симметрии задачи при изменении угла
в силу осевой
симметрии задачи при изменении угла ![]() не меняется.
не меняется.
Дифференциальное уравнение равновесия (1.32,б) для осесимметричной задачи имеет вид
![]() .
(3.1)
.
(3.1)
Напряжения ![]() и
и ![]() выразим через
относительные линейные деформации
выразим через
относительные линейные деформации ![]() с помощью закона Гука:
с помощью закона Гука:
![]() ,
(3.2)
,
(3.2)
а относительные деформации заменим их выражениями через радиальное перемещение v (рис. 30,б), пользуясь зависимостями
![]() .
.
Подставив эти выражения в формулу (3.2), а выражения (3.2) в формулу (3.1), получим выражения для напряжений и дифференциальное уравнение равновесия элемента трубы в перемещениях
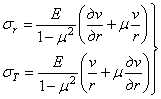 , (3.3)
, (3.3)
![]() . (3.4)
. (3.4)
Уравнение (3.4) может быть представлено в виде
![]() ,
,
откуда следует, что
![]()
Этому уравнению удовлетворяет решение
![]() .
(3.5)
.
(3.5)
Заменив в формулах (3.3) перемещение v его выражением (3.5), получим для напряжений:
 . (3.6)
. (3.6)
Граничные условия для определения постоянных А и В составляем из условий на внутренней и наружной поверхностях трубы:
1) ![]() ,
,
![]() ; 2)
; 2)
![]() ,
,
![]() .
.
Учет этих условий в первом уравнении (3.6) дает систему двух уравнений, содержащих А и В, решив которую, найдем
 .
.
Подстановка найденных значений А и В в уравнения (3.6) дает следующие выражения для напряжений:
 , (3.7)
, (3.7)
а подстановка в уравнение (3.5) - выражение для радиального перемещения
 (3.8)
(3.8)
В формулах (3.7) и (3.8)
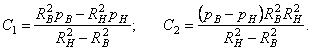
Из формул
(3.7) видно, что
![]()
т. е. сумма радиального и окружного напряжений в любой точке есть постоянная величина, не зависящая от радиуса r.
По формулам (3.7) и (3.8) можно вычислить напряжения и радиальные перемещения для сплошного вала, подверженного наружному радиальному давлению, если положить RB = 0. В таком случае
![]()
откуда видно, что материал вала испытывает однородное напряженное состояние.
3.2 Исследование напряжений при давления на одном из контуров
1. Сжимающее радиальное давление на наружном контуре. По формулам (3.7), положив в них рВ = 0, найдем
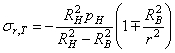 . (3.9)
. (3.9)
Второй член в
скобке формулы (3.9) равен единице или меньше ее, поэтому напряжения ![]() во всех точках
отрицательные, сжимающие. Окружное напряжение по абсолютной величине всегда
больше радиального. Наибольшее нормальное радиальное напряжение
во всех точках
отрицательные, сжимающие. Окружное напряжение по абсолютной величине всегда
больше радиального. Наибольшее нормальное радиальное напряжение ![]() возникает на наружной
поверхности трубы (r
= Rн) и равно - рн,
а наибольшее окружное напряжение
возникает на наружной
поверхности трубы (r
= Rн) и равно - рн,
а наибольшее окружное напряжение ![]() - на
внутренней поверхности (r
= RB)
и равно -
- на
внутренней поверхности (r
= RB)
и равно -
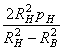 . Как видно из формулы
(3.9), напряжения меняются вдоль радиуса по криволинейному закону. Эпюры
напряжений
. Как видно из формулы
(3.9), напряжения меняются вдоль радиуса по криволинейному закону. Эпюры
напряжений ![]() показаны на рис. 31,а. Уменьшение наружного
радиуса может быть определено по формуле (3.8) для перемещения v, если положить в ней рВ = 0, а r = RB. Тогда
показаны на рис. 31,а. Уменьшение наружного
радиуса может быть определено по формуле (3.8) для перемещения v, если положить в ней рВ = 0, а r = RB. Тогда
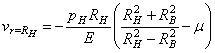 . (3.10)
. (3.10)
2. Сжимающее радиальное давление на внутреннем контуре. По формуле (3.7), положив в рн = 0, найдем
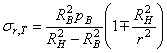 . (3.11)
. (3.11)
а
б
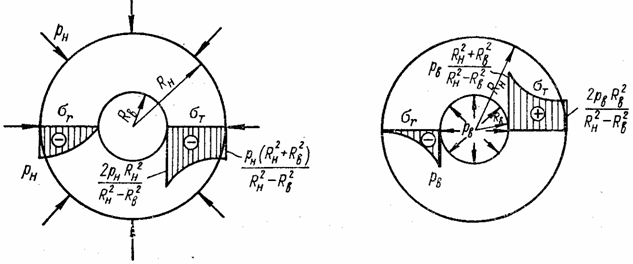
Рис. 31
Второй член в
скобке формулы (3.11) равен единице или больше ее, поэтому напряжения ![]() во всех точках трубы
отрицательны, а
во всех точках трубы
отрицательны, а ![]() -
положительны. Наибольшее нормальное радиальное напряжение
-
положительны. Наибольшее нормальное радиальное напряжение ![]() возникает на
внутренней поверхности (r
= RB)
и равно -
рB, наибольшее окружное
возникает на
внутренней поверхности (r
= RB)
и равно -
рB, наибольшее окружное ![]() - также на внутренней (r = RB), оно
растягивающее и равно
- также на внутренней (r = RB), оно
растягивающее и равно 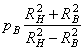 .
.
Закон
изменения напряжений вдоль радиуса тоже криволинейный [см. формулу (3.11)].
Эпюры напряжений ![]() показаны на рис. 31,б.
Увеличение внутреннего радиуса может быть получено по формуле (3.8) для перемещений
v, если положить
в ней рн = 0, a r = RB:
показаны на рис. 31,б.
Увеличение внутреннего радиуса может быть получено по формуле (3.8) для перемещений
v, если положить
в ней рн = 0, a r = RB:
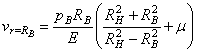 . (3.12)
. (3.12)
Соотношение
окружных напряжений, вычисленных по формуле (3.11) при r = RB
и r == RH ,
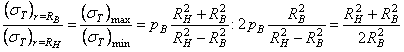 . (3.13)
. (3.13)
Из формулы (3.13) видно, что чем меньше толщина кольца, т. е. чем ближе друг к другу значения RB и RH , тем ближе отношение (3.13) к единице, т. е. тем равномернее распределяются напряжения sT по толщине трубы. Например, при RB = 0,95, отношение
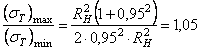
и окружные
напряжения можно считать равномерно распределенными по толщине кольца. При
большой толщине трубы напряжения ![]() и
и ![]() в точках, удаленных от
внутренней поверхности, сближаются по величине и в пределе, при
в точках, удаленных от
внутренней поверхности, сближаются по величине и в пределе, при ![]() , становятся одинаковыми и противоположными по знаку.
, становятся одинаковыми и противоположными по знаку.
Представим формулу (3.11) в виде
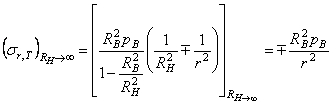 .
.
Следовательно,
если r > 4RB, напряжения
![]() и
и ![]() будут равны и будут
составлять меньше 6% от внутреннего давления. На этом основании по формуле
(3.11) можно определять радиальные и окружные напряжения в случае плоской
деформации тела, имеющего отверстия, нагруженные радиальным давлением, расположенные
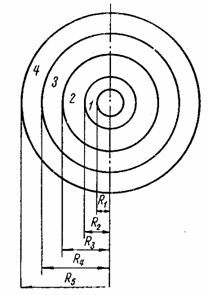
друг от друга на расстоянии больше 8RB (рис. 32). Внешний контур тела не имеет
значения и может быть произвольного очертания.
будут равны и будут
составлять меньше 6% от внутреннего давления. На этом основании по формуле
(3.11) можно определять радиальные и окружные напряжения в случае плоской
деформации тела, имеющего отверстия, нагруженные радиальным давлением, расположенные
друг от друга на расстоянии больше 8RB (рис. 32). Внешний контур тела не имеет
значения и может быть произвольного очертания.
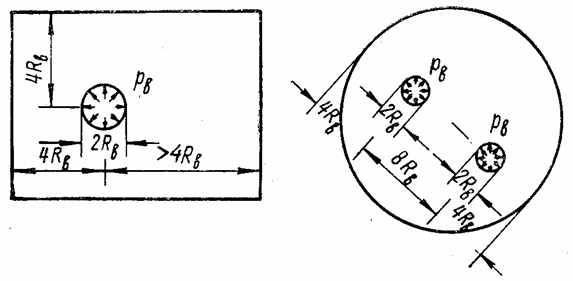
Рис. 32
3.3 Условия прочности при упругой деформации
Составим условия прочности для толстостенной трубы, испытывающей внутреннее давление рВ. В зависимости от принятого предельного состояния для наиболее напряженной точки на внутренней поверхности трубы получим следующие выражения:
1. Для хрупких материалов (чугун, бетон) по первой теории прочности
![]() . (3.14)
. (3.14)
По формуле (3.11) при r = RB расчетное напряжение
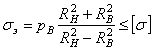 .
.
или
![]() ,
,
откуда
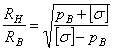 .
(3.15)
.
(3.15)
Выражение
(3.15) показывает, что при внутреннем давлении, приближающемся по величине к
допускаемому напряжению ![]() ,
отношение
,
отношение ![]() стремится к бесконечности, т.е. никаким увеличением
наружного радиуса RH
нельзя удовлетворить условию прочности (3.14).
стремится к бесконечности, т.е. никаким увеличением
наружного радиуса RH
нельзя удовлетворить условию прочности (3.14).
2. Для пластичных материалов (сталь, медь) по третьей теории прочности
![]() . (3.16)
. (3.16)
По формуле (3.11) при r = RB расчетное напряжение
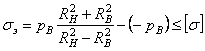 . (3.16)
. (3.16)
или
![]() ,
,
откуда
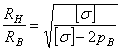 . (3.17)
. (3.17)
Выражение
(3.17) показывает, что при внутреннем давлении рВ,
приближающемся по величине к половине допускаемого напряжения ![]() , отношение
, отношение ![]() стремится к
бесконечности и увеличением наружного радиуса РH удовлетворить условию прочности (3.16)
нельзя.
стремится к
бесконечности и увеличением наружного радиуса РH удовлетворить условию прочности (3.16)
нельзя.
3.4 Напряжения в составных трубах.
Имеются
конструкции, представляющие собой составные толстостенные оболочки или трубы
(например, стволы артиллерийских орудий, облицовки пустотелых гребных винтов)
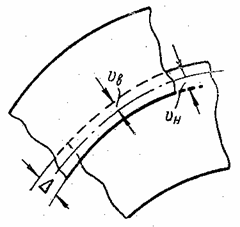
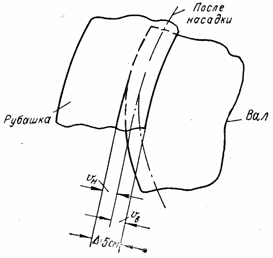
(рис. 33,а). В этих случаях наружные оболочки насаживаются на внутренние
с натягом ![]() (рис. 33,б).
Геометрическое условие совместности деформаций внутренней и наружной трубы
имеет вид
(рис. 33,б).
Геометрическое условие совместности деформаций внутренней и наружной трубы
имеет вид
![]() ,
,
где vB - уменьшение наружного радиуса внутренней трубы;
vH - увеличение внутреннего радиуса наружной трубы.
Подставив в уравнение (3.18) абсолютные величины радиальных перемещений vB и vH по формулам (3.12) и (3.10) с учетом обозначений, принятых для радиусов на рис. 33, получим
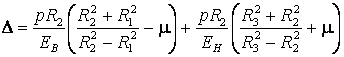 ,
(3.19)
,
(3.19)
где р - междутрубное давление, действующее на поверхности соприкосновения труб;
ЕB и ЕH - модули упругости материала внутренней и наружной труб.
|
а |
б |
|
|
|
|
Рис. 33 |
|
Применительно к трубам, выполненным из одинакового материала с модулем упругости Е, формула (3.19) примет вид
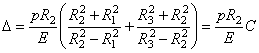 ,
(3.20)
,
(3.20)
где введено обозначение
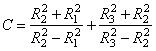 . (3.20)
. (3.20)
Решение уравнения (3.20) дает следующее выражение для междутрубного давления:
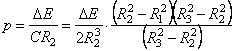 . (3.21)
. (3.21)
При заданном
натяге ![]() для возможности
насадки наружной трубы на внутреннюю нужно или нагреть наружную трубу или
охладить внутреннюю.
для возможности
насадки наружной трубы на внутреннюю нужно или нагреть наружную трубу или
охладить внутреннюю.
Натяг ![]() связан с температурой t соотношением
связан с температурой t соотношением
![]() .
(3.22)
.
(3.22)
Приравняв правые части уравнений (3.20) и (3.22), получим междутрубное давление после насадки
![]() .
(3.23)
.
(3.23)
Напряжения в
составной трубе вычисляются на основании принципа сложения действия сил путем
алгебраического суммирования рабочих напряжений от внутреннего давления рB сплошной трубы с внутренним радиусом R1 и наружным R3
(соответствующие эпюры показаны на рис. 33,в) и напряжений от междутрубного давления р. Для внутренней трубы междутрубное давление представляет собой наружную
радиальную сжимающую нагрузку, а для наружной - внутреннюю радиальную
сжимающую нагрузку. Эпюры от междутрубного давления р показаны на рис. 33,г, а суммарные эпюры
напряжений ![]() и
и ![]() на рис. 33,д.
на рис. 33,д.
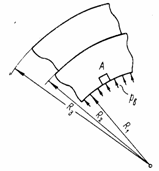
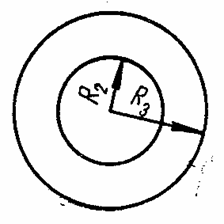
Пользуясь
одной из теорий прочности, можно при заданном наружном радиусе R2 внутренней
трубы определить величину возможного полного радиального давления р, действующего по поверхности
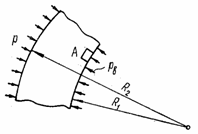
соприкосновения труб, из условия, что расчетное напряжение ![]() по выбранной теории
прочности в наиболее напряженных точках А и В (рис. 34) трубы
равняется допускаемому напряжению
по выбранной теории
прочности в наиболее напряженных точках А и В (рис. 34) трубы
равняется допускаемому напряжению ![]() .
.
|
а |
б |
в |
|
|
|
|
|
Рис. 34 |
||
В точке А
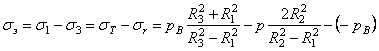 .
(3.24)
.
(3.24)
В точке В
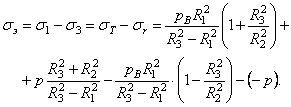 (3.25)
(3.25)
Если
приравнять выражение (3.24) для напряжения ![]() в точке А
допускаемому напряжению
в точке А
допускаемому напряжению ![]() , полное радиальное давление р
на поверхности соприкосновения труб получится из уравнения
, полное радиальное давление р
на поверхности соприкосновения труб получится из уравнения
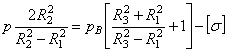
следующим:
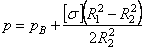 . (3.26)
. (3.26)
Наружный радиус R3 наружной трубы определяется при известной величине давления р из условия прочности для элемента, выделенного у точки В на внутренней поверхности наружной трубы (рис. 34,в). По третьей теории прочности аналогично (3.16)
![]() ,
(3.27)
,
(3.27)
а по формуле
(3.11) при радиусах RВ = R2, RН = R3 и r = R2
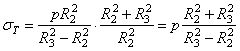 . (3.28)
. (3.28)
Приравняв выражения (3.27) и (3.28), найдем
![]()
откуда
![]() .
(3.29)
.
(3.29)
Условие равнопрочности труб в точках А и В получится путем приравнивания выражений (3.23) и (3.24) для напряжения в этих точках:
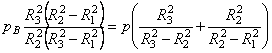 .
.
Если
подставить выражение (3.21) для междутрубного давления
в формулу (3.24) для расчетного напряжения, ![]() последняя получит
вид:
последняя получит
вид:
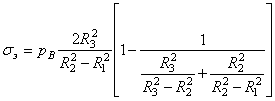 .
.
Расчетное
напряжение ![]() для составной трубы
будет иметь наименьшее значение. Тогда, когда отрицательное слагаемое в
квадратных скобках будет наибольшим. Это произойдет при значении
для составной трубы
будет иметь наименьшее значение. Тогда, когда отрицательное слагаемое в
квадратных скобках будет наибольшим. Это произойдет при значении ![]() при этом квадратная
скобка будет равна
при этом квадратная
скобка будет равна ![]() , а наименьшее
расчетное напряжение
, а наименьшее
расчетное напряжение
![]() .
.
В разделе 3.3
по третьей теории прочности была получена формула для расчетного напряжения ![]() сплошной трубы, подверженной
внутреннему давлению. Насколько уменьшается это напряжение у составной трубы,
показывает соотношение
сплошной трубы, подверженной
внутреннему давлению. Насколько уменьшается это напряжение у составной трубы,
показывает соотношение
![]() .
.
При малом
внутреннем радиусе R1
это отношение приближается к 0,5. Если же наружный радиус R3 близок по значению
внутреннему радиусу R1
, т. е. труба тонкостенная, отношение ![]() становится близким к единице, т. е. составная труба не имеет
прочностных преимуществ по сравнению со сплошной.
становится близким к единице, т. е. составная труба не имеет
прочностных преимуществ по сравнению со сплошной.
3.5 Понятие о расчете многослойных труб
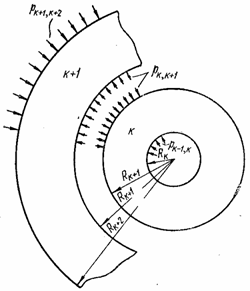
Выражение (3.8), полученное для радиальных перемещений v трубы, подверженной радиальным давлениям на наружное и внутреннем контурах, может быть использовано для определения междутрубных давлений рм в многослойных трубах (рис. 35,а), возникающих от посадки. Рассмотрим два последовательных слоя k и k + 1 многослойной трубы (рис. 35,б). Каждый слой представляет собой трубу, находящуюся в условиях, соответствующих схеме нагружения на рис. 35,а, и радиальное давление на наружном контуре каждого слоя (трубы) является сжимающим. Поэтому в формуле для перемещения v давление рН нужно считать положительным. Для каждой поверхности соприкосновения между k-м и (k + 1)-м слоями можно написать уравнение совместности деформации
![]() .
.
|
а |
б |
|
|
|
|
Рис. 35 |
|
Уравнение
(3.30) выражает условие равенства суммы укорочения ![]() наружного радиуса внутреннего слоя k и удлинения
наружного радиуса внутреннего слоя k и удлинения ![]() внутреннего радиуса
наружного слоя k
+ 1 величине натяга
внутреннего радиуса
наружного слоя k
+ 1 величине натяга ![]() между слоями k и k + 1.
между слоями k и k + 1.
Для вычисления
перемещения ![]() в формулу для перемещения
(3.8) нужно подставить
в формулу для перемещения
(3.8) нужно подставить
![]()
Для вычисления
перемещения ![]() в формулу (3.8) нужно
подставить
в формулу (3.8) нужно
подставить
![]()
После подстановки и некоторых упрощений для труб, выполненных из одного материала (Е и m одинаковы), уравнение совместности (3.30) примет вид
 . (3.31)
. (3.31)
Уравнение (3.31) называется уравнением трех давлений. Если число слоев составной трубы равно п, то число уравнений (3.31), составляемых для каждой поверхности соприкосновения слоев, будет п — 1. Число содержащихся в них неизвестных междутрубных давлений будет тоже п — 1, следовательно, путем совместного решения уравнений системы давления могут быть всегда найдены. Следует отметить, что для ненагруженных внутренней и наружной поверхностей составной трубы, состоящей из п слоев, давления р0,1 и рn,n+1 равны нулю.
После определения междутрубных давлений, напряжения в каждом промежуточном слое, возникающие от натяга, определяются по формулам (3.7), во внутреннем слое - по формулам (3.9), а в наружном - по формулам (3.11). К полученным напряжениям следует алгебраически добавить напряжения, полученные для сплошной трубы, имеющей такую же толщину, как и составная, от внутреннего или наружного давления, которому подвергается составная труба.
3.6 Примеры
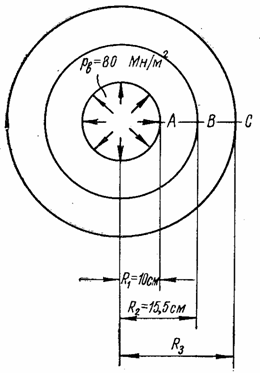
Пример 3.1.
Определить, пользуясь третьей теорией прочности (наибольших касательных
напряжений), наружный радиус R3
составной трубы (рис. 36,а), подверженной внутреннему давлению рВ = 80 Мн/м2, если допускаемое напряжение ![]() не должно превышать
150 Мн/м2. Построить эпюры
радиальных и окружных напряжений по сечению А - С.
не должно превышать
150 Мн/м2. Построить эпюры
радиальных и окружных напряжений по сечению А - С.
|
а |
б |
|
|
|
|
Рис. 36 |
|
Решение. Материал трубы испытывает плоскую деформацию. Для внутренней трубы наиболее напряженными являются точки на внутренней поверхности, в которых радиальное и окружное главные напряжения, (рис. 36,б) одновременно достигают наибольшей величины. Так как в этих точках окружное напряжение больше, чем радиальное, а радиальное - сжимающее и равно внутреннему давлению рВ, то
![]() .
.
Окружное напряжение в точке А на внутренней поверхности согласно формуле (3.24)
![]() .
.
Полное
давление р по поверхности соприкосновения труб,
соответствующее при заданном радиусе R2 допускаемому напряжению ![]() в точке А, по
формуле (3.26)
в точке А, по
формуле (3.26)
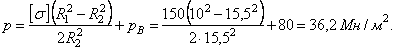
Наружный радиус R3 наружной трубы по формуле (3.29)
![]()
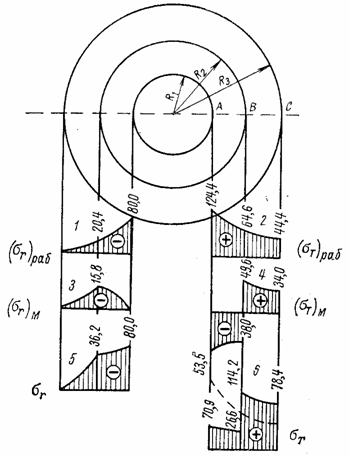
Рис. 37
Эпюры напряжений строятся отдельно (рис. 37):
1) для
радиальных и окружных рабочих напряжений (![]() )раб и (
)раб и (![]() )раб от внутреннего давления рВ в сплошной трубе, имеющей толщину
стенки R3
- R1 (эпюры 1 и 2);
)раб от внутреннего давления рВ в сплошной трубе, имеющей толщину
стенки R3
- R1 (эпюры 1 и 2);
2) для
напряжении (![]() )м и (
)м и (![]() )м от междутрубного
сжимающего давления рм,
возникающего от насадки: у внутренней трубы - наружного радиального и
у наружной трубы -
внутреннего радиального (эпюры 3 и 4).
)м от междутрубного
сжимающего давления рм,
возникающего от насадки: у внутренней трубы - наружного радиального и
у наружной трубы -
внутреннего радиального (эпюры 3 и 4).
Полные эпюры
напряжений ![]() и
и ![]() (эпюры 5 и 6) получаются сложением ординат указанных двух эпюр с
учетом их знаков
(эпюры 5 и 6) получаются сложением ординат указанных двух эпюр с
учетом их знаков
![]()
Величина междутрубного давления рм
определяется из условия, что по поверхности соприкосновения труб полное
радиальное напряжение ![]() равно сумме междутрубного давления (
равно сумме междутрубного давления (![]() )м
и рабочего напряжения (
)м
и рабочего напряжения (![]() )раб, возникающего в этом месте сплошной
трубы, имеющей толщину стенки R3 — R1, от внутреннего давления рB. Но так как (
)раб, возникающего в этом месте сплошной
трубы, имеющей толщину стенки R3 — R1, от внутреннего давления рB. Но так как (![]() )м в точке В равнo
рм, a
)м в точке В равнo
рм, a ![]() равно р, то
равно р, то
![]()
откуда
![]()
Напряжение (![]() )раб вычисляется по формуле (3.11) для
радиального напряжения по поверхности с радиусом r =
15,5 см в сплошной трубе толщиной R3 - R1,
подверженной одному внутреннему давлению рB = 80 Мн/м2,
)раб вычисляется по формуле (3.11) для
радиального напряжения по поверхности с радиусом r =
15,5 см в сплошной трубе толщиной R3 - R1,
подверженной одному внутреннему давлению рB = 80 Мн/м2,
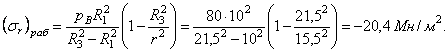
По формуле (3.22)
![]()
По этим
значениям (![]() )раб и (
)раб и (![]() )м построены эпюры 1 и 3 на рис.
37. Алгебраическое сложение ординат этих эпюр дает ординаты эпюры 5 полного радиального напряжения.
)м построены эпюры 1 и 3 на рис.
37. Алгебраическое сложение ординат этих эпюр дает ординаты эпюры 5 полного радиального напряжения.
Определим
окружное напряжение (![]() )м
от междутрубного давления рм
по поверхности соприкасания труб. Для наружной трубы,
испытывающей внутреннее давление рм
, оно определяется по формуле (3.11):
)м
от междутрубного давления рм
по поверхности соприкасания труб. Для наружной трубы,
испытывающей внутреннее давление рм
, оно определяется по формуле (3.11):
- в точке В (r = R2)
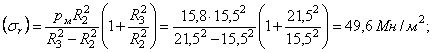
- в точке С (r = R3)
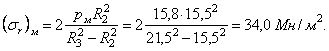
Для внутренней
трубы, испытывающей наружное давление рм,
(![]() )м,
оно определяется по формуле (3.9):
)м,
оно определяется по формуле (3.9):
- в точке В (r = R2)
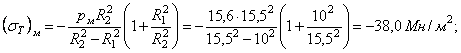
- в точке А (r = R1)
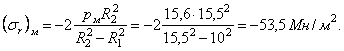
Окружное
напряжение (![]() )раб
от давления рВ вычисляем по формуле
(3.11), приняв в ней RB
= R1, RH = R3:
)раб
от давления рВ вычисляем по формуле
(3.11), приняв в ней RB
= R1, RH = R3:
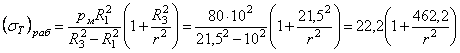 . (3.23)
. (3.23)
По формуле
(3.23) вычисляем:
- в
точке. А при r = 10 см (![]() )раб
= 124,4 Мн/м2;
)раб
= 124,4 Мн/м2;
- в
точке В при r = 15,5 см
(![]() )раб
= 64,6 Мн/м2;
)раб
= 64,6 Мн/м2;
- в
точке С при r =
21,5 см (![]() )раб
= 44,4 Мн/м2.
)раб
= 44,4 Мн/м2.
По этим
значениям (![]() )раб
и (
)раб
и (![]() )м
построены эпюры 2 и 4. Алгебраическое сложение ординат
этих эпюр дает ординаты эпюры 6
полного окружного напряжения
)м
построены эпюры 2 и 4. Алгебраическое сложение ординат
этих эпюр дает ординаты эпюры 6
полного окружного напряжения ![]() .
.
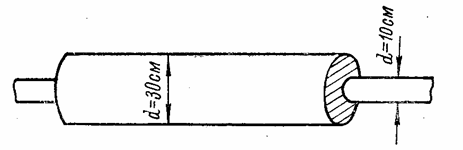
Пример 3.2.
На вал диаметром d = 10 см в горячем состоянии надета рубашка (рис. 38, а),
внутренний диаметр которой до нагревания был на 0,001d меньше диаметра вала. Толщина стенок рубашки 10 см. Вал и рубашка стальные.
Определить наибольшие напряжения в рубашке (Е = 2![]() Мн/м2).
Мн/м2).
|
а |
|
|
|
|
|
б |
|
|
|
|
|
Рис. 38 |
|
Решение.
Уменьшение радиуса вала и увеличение внутреннего радиуса рубашки в сумме должны
дать величину зазора ![]() между рубашкой и валом
до нагревания, равного (рис. 38,б)
между рубашкой и валом
до нагревания, равного (рис. 38,б)
![]()
Для решения
задачи следует использовать формулы для составных труб, полагая внутренний
радиус внутренней трубы R1 равным нулю, R2 = 5 см и R3 = 15 см.
Давление, передающееся от рубашки на вал после насадки, по формуле (3.20)
![]()
где
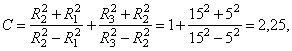
тогда
![]()
Наибольшее по абсолютной величине радиальное напряжение в рубашке возникает по поверхности соприкосновения с валом:
![]()
Наибольшее окружное напряжение в рубашке возникает на ее внутренний поверхности [см. формулу (3.11)]:
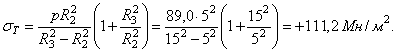
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов