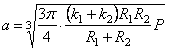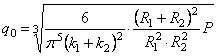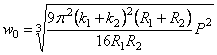Лекция 2. Простейшие осесимметричные задачи
2.1 Уравнения в цилиндрических
координатах
Представим тело
вращения, к которому приложены силы, расположенные симметрично относительно оси
этого тела (рис.18). Примерами могут быть круглый цилиндр, усеченный конус,
деформирующийся под действием равномерного внутреннего или наружного давления
или сил, равномерно приложенных по торцевым сечениям.
За ось
вращения примем ось z,
ось же перпендикулярную к ней, обозначим через r. Двух координат z и r вполне
достаточно, так как все точки с одинаковыми такими координатами находятся в
одинаковых условиях.
Так как каждая
меридиональная плоскость z0r представляет плоскость
симметрии как в отношении формы, так и в отношении
нагрузки тела, то в меридиональных плоскостях касательных напряжений быть не
может. Поэтому для каждой точки тела, расположенной на меридиональной
плоскости, площадка, содержащая эту точку, является главной площадкой
рассматриваемого напряженного состояния. Главное напряжение, действующее по
этой площадке, обозначим через 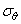 .
.
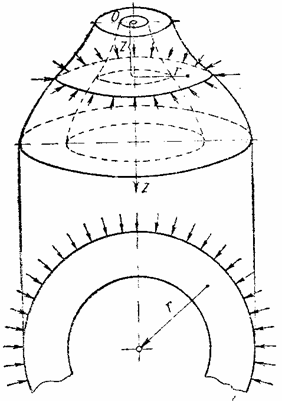
Рис.18
Кроме меридионального сечения через точку с координатами z, r проведем еще второе сечение,
перпендикулярное к оси z, и третье
сечение, перпендикулярное к двум первым. Следы этих двух секущих плоскостей на
меридиональной плоскости будут параллельны соответственно осям r и z.
Вследствие
симметрии в обеих секущих плоскостях, в точке z,
r могут
действовать лишь такие касательные напряжения, которые параллельны
меридиональной плоскости (рис. 19). Нормальные напряжения, действующие в
секущих плоскостях, обозначим через 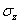 и
и 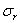 , касательные — через
, касательные — через 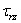 и
и 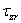 . Эти напряжения надо считать функциями от z и r.
. Эти напряжения надо считать функциями от z и r.
Указанные выше
условия задачи характеризуют случай, когда основные уравнения упругого
равновесия можно представить в такой же простой форме, как и в случае плоской
задачи, и потому можем ограничиться рассмотрением соотношений, имеющих место
для точек одной и той же плоскости.
0 r
z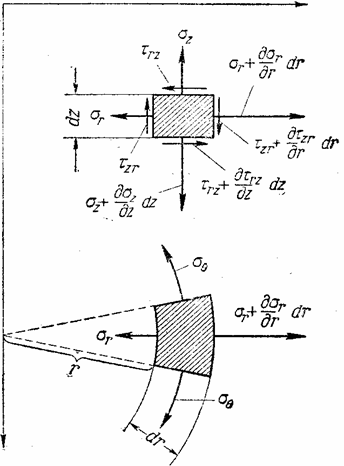
Рис.19
Проектируя все
усилия, принадлежащие элементарному объему на оси z
и r, имеем
уравнения равновесия в виде:
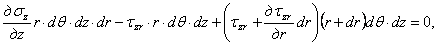
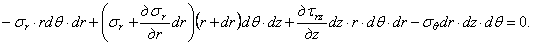
После
сокращения на общий множитель 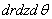 статические уравнения
запишутся:
статические уравнения
запишутся:
 (2.1)
(2.1)
Обозначая
упругие перемещения точки в направлении оси z через w, в направлении радиуса через и (в тангенциальном
направлении перемещение отсутствует), геометрические уравнения для
данного случая можем представить в виде
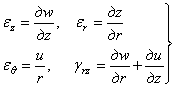 . (2.2)
. (2.2)
Наконец,
физические уравнения, согласно (1.24)
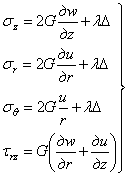 .
(2.3)
.
(2.3)
При решении
задачи в перемещениях объемное расширение
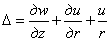
может быть
переписано в виде
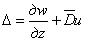 ,
(2.4)
,
(2.4)
где под 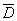 надо понимать
обозначение следующей операции:
надо понимать
обозначение следующей операции:
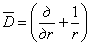 .
.
Подставляя
(2.4) в физические уравнения (2.3), и, далее, в уравнения равновесия (2.1),
придаем последним вид
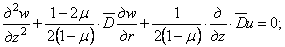 (2.5)
(2.5)
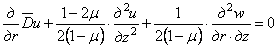 . (2.6)
. (2.6)
Таким образом,
задача определения напряжений в теле вращения, загруженном симметрично
относительно оси, сводится к нахождению двух функций w и и, которые должны удовлетворять в
каждой точке уравнениям (2.5) и (2.6) и одновременно граничным условиям на
поверхности тела.
Если, кроме
того, ввести оператор 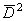 , положив
, положив
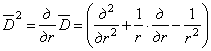 ,
,
то из уравнений (2.5) и (2.6), исключая из них w,
дифференцируя (2.5) по z
и r и подставляя
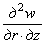 из (2.6), получим:
из (2.6), получим:
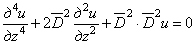 . (2.7)
. (2.7)
Аналогично
можно составить дифференциальное уравнение, которому должно удовлетворять перемещение
w, если к
уравнению (2.6) сначала применить операцию 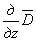 , а затем вставить
, а затем вставить 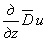 из уравнения (2.5):
из уравнения (2.5):
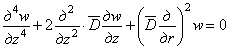 . (2.8)
. (2.8)
Установленные
уравнения теории упругости в напряжениях (уравнения неразрывности деформаций,
выраженные через напряжения), написанные в декартовых координатах, можно
преобразовать к цилиндрическим координатам,
Для этой цели
надлежит выразить напряжения 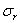 и
и 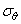 через
через
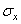 и
и 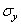 по известным формулам
перехода
по известным формулам
перехода
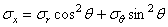 ;
; 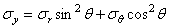
заменив запись
суммы другой:
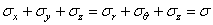 ,
,
но учесть, что
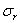 и
и 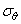 не зависят от угла
не зависят от угла 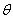 ,
тогда как
,
тогда как 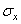 и
и 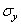 являются функциями
являются функциями 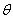 .
.
Запишем
окончательные результаты для уравнений совместности, которых ввиду осесимметричного характера деформаций останется четыре:
 , (2.9)
, (2.9)
где введен
символ
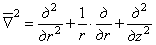 .
(2.10)
.
(2.10)
Заметим, что
одновременно с уравнениями неразрывности должны быть удовлетворены уравнения
равновесия (2.1) и условия на контуре.
Подобно тому,
как в плоской задаче теории упругости удалось все компоненты напряжений
выразить через одну функцию напряжений, так и в разбираемом осесимметричном
пространственном случае имеется такая же возможность.
В самом деле,
если задаться
 , (2.11)
, (2.11)
где 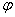 - произвольная
функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно
обратится в тождество. Второе уравнение равновесия и все уравнения
неразрывности будут удовлетворены, если принять
- произвольная
функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно
обратится в тождество. Второе уравнение равновесия и все уравнения
неразрывности будут удовлетворены, если принять 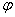 согласно уравнению
согласно уравнению
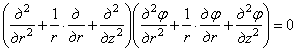 . (2.12)
. (2.12)
Можно
подобрать много решений уравнения (2.12). Вот некоторые из них:
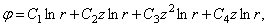 (2.13)
(2.13)
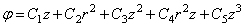 .
(2.14)
.
(2.14)
Так как эти
выражения 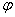 удовлетворяют
уравнению (2.12) при любых значениях коэффициентов С,
следовательно, любой член их также удовлетворяет уравнению (2.12). Например,
может быть
удовлетворяют
уравнению (2.12) при любых значениях коэффициентов С,
следовательно, любой член их также удовлетворяет уравнению (2.12). Например,
может быть
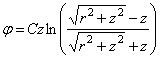 .
(2.15)
.
(2.15)
Если в числе
прочих причиной, вызывающих напряженное и деформированное состояния тела,
является возникновение температурного поля, в общем случае неравномерного
вдоль координаты z
и вдоль радиуса r, т. е.
T = T(z,r) ,
то надлежит внести дополнения в физические уравнения (2.3), а
именно, они должны быть записаны [(по аналогии с (1.47), но в цилиндрических
координатах] следующим образом:
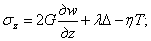 (2.16)
(2.16)
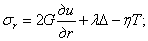 (2.17)
(2.17)
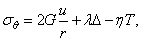 (2.18)
(2.18)
где, введено
обозначение:
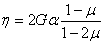 .
.
В качестве
примера рассмотрим длинную толстостенную трубу (рис. 20) с радиальным перепадом
температур, т. е. считается заданным
закон Т = Т ( r ).
Пренебрегая
влиянием торцов, можно считать, что все сечения трубы, перпендикулярные к ее
оси, остаются плоскими и все работают в одинаковых условиях. Таким образом,
радиальное перемещение u
зависит только от r,
перемещение v в
направлении 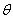 отсутствует,
относительное удлинение по направлению оси z следует считать постоянным, т. е.
отсутствует,
относительное удлинение по направлению оси z следует считать постоянным, т. е.
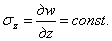 (2.19)
(2.19)
Для
относительных удлинений в радиальном и тангенциальном направлениях
возможно использовать соотношения (1.35,а),
(1.35,б) т. е.
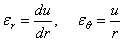 .
(2.20)
.
(2.20)
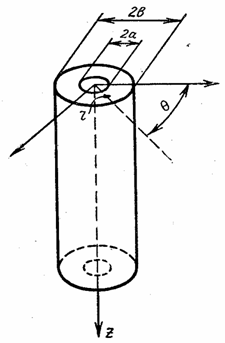
Рис. 20
Очевидно в рассматриваемой задаче сохраняется уравнение
равновесия из (1.32,б) т.е.
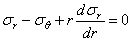 . (2.21)
. (2.21)
Использование
(2.19) (2.20) в (2.16) и (2.18) с последующей подстановкой в (2.21) приводит к
разрешающему уравнению следующего вида:
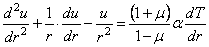 . (2.22)
. (2.22)
Решением
(2.22) является выражение
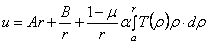 .
(2.23)
.
(2.23)
где 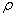 - переменная
интегрирования.
- переменная
интегрирования.
Далее,
очевидно, подлежит подставить (2.23) в (2.17), (2.18), а для определения
постоянных А, В и 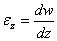 использовать граничные
уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то,
следовательно:
использовать граничные
уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то,
следовательно:
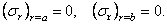
Если труба не имеет
осевой нагрузки, то
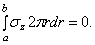
Приведем
окончательные выражения для напряжений на внутренней и наружной поверхности
трубы для случая, когда на этих поверхностях поддерживаются постоянные
температуры Та и Тb и,
следовательно, для такого установившегося потока распределение температур по
толщине стенки выражается формулой:
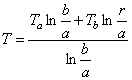 .
(2.24)
.
(2.24)
Тогда на
внутренней и наружной поверхностях:
 (2.25)
(2.25)
 . (2.26)
. (2.26)
2.2 Деформация толстостенного сферического сосуда
При решении
некоторых задач, когда многие компоненты напряжений и деформаций отсутствуют,
можно не прибегать к общим уравнениям теории упругости (в перемещениях или в
напряжениях), которые должны значительно упроститься, а все три необходимые
стороны исследования (геометрическую, физическую и статическую) выполнить
непосредственно применительно к рассматриваемому частному случаю.
Представим
себе шаровой сосуд, подвергающийся действию внутреннего и внешнего равномерных
давлений. Пусть а и b
обозначают соответственно внутренний и наружный радиусы шара (рис. 21), а рa и рb - внутреннее
и наружное давления газов.
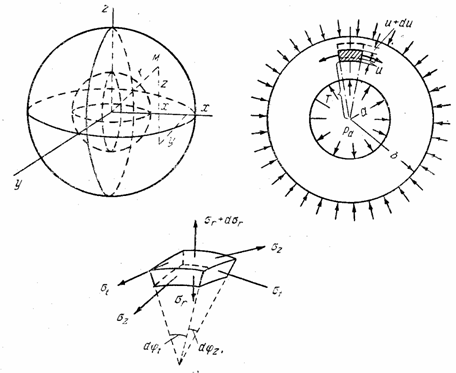
Рис. 21
Начнем со
статического обследования. Вырежем для исследования бесконечно малый элемент
двумя парами взаимно перпендикулярных меридиональных сечений и двумя
концентрическими сферическими поверхностями. Действие отброшенных частей
сосуда заменим тангенциальными (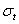 ,
, 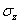 ) и радиальными (
) и радиальными (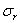 ) напряжениями. Так как в рассматриваемом случае напряжения
зависят только от радиуса r, то
напряжения по двум бесконечно близким друг к другу концентрическим поверхностям
будут отличаться на величину
) напряжениями. Так как в рассматриваемом случае напряжения
зависят только от радиуса r, то
напряжения по двум бесконечно близким друг к другу концентрическим поверхностям
будут отличаться на величину 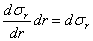 и не будут
зависеть от угла
и не будут
зависеть от угла 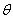 -
другого параметра, определяющего местоположение рассматриваемого элемента.
Проектируя все силы на нормаль к элементу, имеем уравнение равновесия в виде:
-
другого параметра, определяющего местоположение рассматриваемого элемента.
Проектируя все силы на нормаль к элементу, имеем уравнение равновесия в виде:
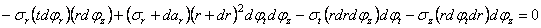 .
.
Имея в виду
равенство 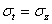 и производя
сокращения, получаем уравнение равновесия:
и производя
сокращения, получаем уравнение равновесия:
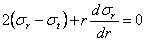 . (2.27)
. (2.27)
Переходим к
геометрическому обследованию. Из рассмотрения перемещений и формоизменения
элемента заключаем, что относительное тангенциальное удлинение:
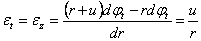 , (2.28)
, (2.28)
а
относительное радиальное удлинение:
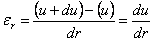 . (2.29)
. (2.29)
Выполним
физическое обследование. Зависимость напряжений от деформаций в данном случае
имеет вид:

Напряжения
через деформации выражаются (принимая во внимание равенство 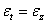 и
и 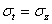 ) так:
) так:
 . (2.30)
. (2.30)
Данные
геометрического обследования используем для преобразования полученных
физических зависимостей, т. е. подставляем (2.28) и (2.29) в (2.30). Имеем
выражения для напряжений:
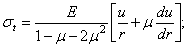 (2.31)
(2.31)
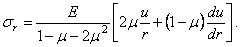 (2.32)
(2.32)
Выражения
(2.31) и (3.32) подставляем в уравнение статики (12.27). Тогда после сокращений получаем выражение
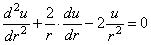 , (2.33)
, (2.33)
которое
представляет собой уравнение, объединяющее в себе все три стороны исследования
(геометрическую, физическую и статическую).
Общий интеграл
дифференциального уравнения (2.33) имеет вид
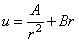 .
(2.34)
.
(2.34)
Дифференцируя
(2.34), находим
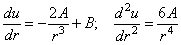 . (2.35)
. (2.35)
Подставляя
(2.34) и (2.35) в (2.31) и (2.32), получаем вместо дифференциальной формы
выражения для напряжений в алгебраической форме:
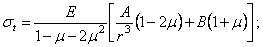 (2.36)
(2.36)
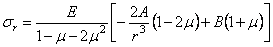 . (2.37)
. (2.37)
Постоянные
интегрирования А и В определим из поверхностных
условий:
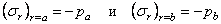 .
.
Тогда, в силу
(2.37), имеем:


откуда
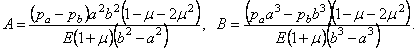 (2.38)
(2.38)
Подставляя
(2.38) в (2.36) и (2.37), окончательно получим:

Для случая
одного внутреннего давления рa
наибольшее растягивающее тангенциальное напряжение будет на внутренней
поверхности сосуда (при r = a):
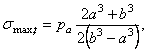
а минимальное на наружной поверхности (при r
= b):
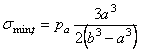 .
.
Приведенное
здесь решение задачи теории упругости получено применением метода перемещений.
2.3. Сосредоточенная сила, действующая на плоскость
Пусть
плоскость z = 0
является гранью полубесконечного сплошного тела пусть на эту плоскость действует
сосредоточенная сила Р по оси z (рис. 22). В литературе эта задача именуется задачей Буссинеска.
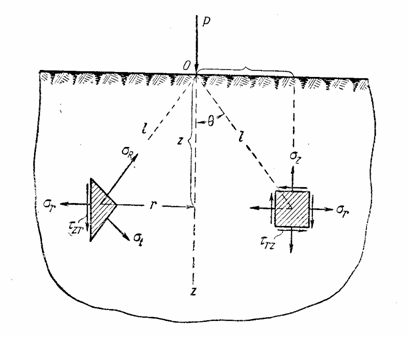
Рис. 22
Для
радиального напряжения можно принять в качестве первой попытки
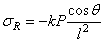 .
.
Переходя к
цилиндрическим координатам, по формулам перехода должны получить
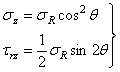 .
.
Заменяя 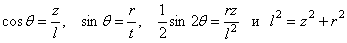 , имеем:
, имеем:
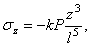 (2.39)
(2.39)
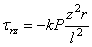 .
(2.40)
.
(2.40)
Для
определения коэффициента k
составим уравнение равновесия по какому-либо горизонтальному сечению z = a. Для элементарной площадки в виде
бесконечно тонкого кольца шириной dr и радиуса r имеем элементарную внутреннюю
силу
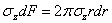 .
.
Со всех таких
элементарных площадок, т. е. со всего сечения z = a, имеем сумму внутренних усилий
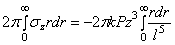 . (2.41)
. (2.41)
Так как 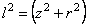 , то, дифференцируя, имеем 2ldl
= 2rdr.
Таким образом, (2.41) перепишется:
, то, дифференцируя, имеем 2ldl
= 2rdr.
Таким образом, (2.41) перепишется:
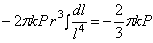 .
.
Уравнение
равновесия по сечению z = а (сумма проекций на ось z)
приводит к выражению
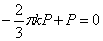 ,
,
откуда 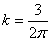 .
.
То, что
выражения (2.39) и (2.40) дают точное решение задачи, можно доказать путем
использования функции напряжений. Выполнение этой операции позволит определить
нам также и другие компоненты напряжений (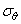 ,
, 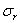 ).
).
На основании
(2.13, 2.14, 2.15)
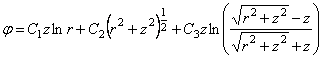 .
.
Окончательно
формулы для напряжений примут вид:
 . (2.42)
. (2.42)
Для определения
перемещений используем уравнения (2.2). Компонента смещения вдоль радиуса r
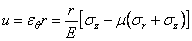 . (2.43)
. (2.43)
После
подстановки в (2.43) выражений (2.42) и преобразований получаем
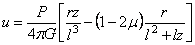 .
.
При 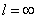 ,
как и следует ожидать, и == 0. На основании этого
,
как и следует ожидать, и == 0. На основании этого
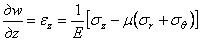 ,
,
откуда
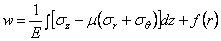 . (2.44)
. (2.44)
После
подстановки в (2.44) выражений (2.42) и интегрирования, принимая также, что 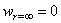 , получаем:
, получаем:
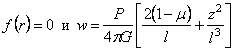 .
.
Для
вертикальных перемещений точек на граничной плоскости z = 0 для так называемой “дневной
поверхности” получим выражение:
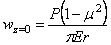 .
(2.45)
.
(2.45)
У начала
координат, как это было и в плоской задаче, перемещения и напряжения становятся
бесконечно большими, и потому, необходимо представить, что у начала координат
в области пластических деформаций материал вырезан полусферической
поверхностью малого радиуса, а сосредоточенная сила Р
заменена статически эквивалентными усилиями, распределенными по этой
поверхности.
Полное
напряжение в любой точке горизонтальной площадки (т.е. равнодействующая
напряжений 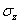 и
и
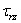 на рис. 23)
на рис. 23)
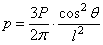 .
.
Если, далее,
очертить произвольным диаметром d сферу, касающуюся граничной плоскости в той же точке O,
то по всем горизонтальным площадкам, размещенным на поверхности этой сферы,
полные напряжения
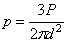 .
.
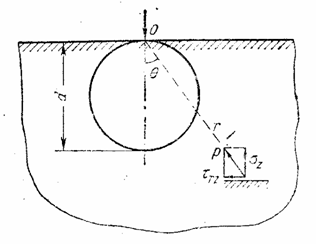
Рис. 23
2.4 Частные случаи загрузки упругого
полупространства
а)
Равномерная загрузка по площади круга. Имея решение для сосредоточенной
силы, действующей на плоскую грань упругого полупространства, найдем
перемещения и напряжения, возникающие под действием распределенной нагрузки, если применим принцип
сложения действия сил. Пусть нагрузка общим весом Р
равномерно распределена на "дневной" поверхности полубесконечного
тела по площади круга радиуса а. Интенсивность нагрузки
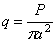 .
.
Составим
выражения для перемещения точки С, находящейся
на "дневной" поверхности, но в пределах загруженного круга (рис.
24).
Проведем через
точку С секущую МС, а в
бесконечной близости другую – М1С и рассмотрим влияние на "прогиб"
точки С нагрузки, расположенной на элементарной площадке,
заштрихованной на рис. 24.
Эта площадка равна dF=sd ds, а нагрузка, на нее
приходящаяся,
ds, а нагрузка, на нее
приходящаяся,
dP = qdF = qsd ds. (2.46)
ds. (2.46)
От такой
нагрузки точка С должна опуститься согласно
(2.45) на
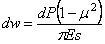
и тогда
получим
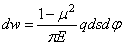 .
.
Полное
перемещение точки С
от всей нагрузки
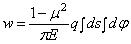 .
.
Из рис. 24 ясно, что взятый по всей
длине секущей интеграл
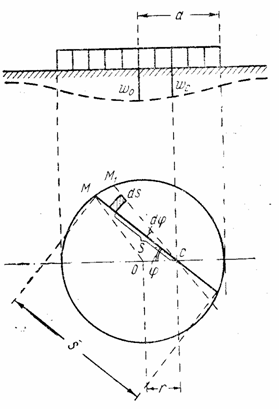
Рис. 24
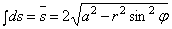 . (2.47)
. (2.47)
Тогда
окончательно
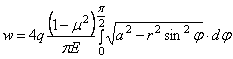 .
.
Для “прогиба”
в центре круга, т. е. при r
= 0, имеем:
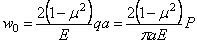 .
.
Таким образом,
зная а, избавимся от
бесконечности, получаемой по формуле (2.45).
Для “прогиба” точек, лежащих на контуре загруженного круга, т. е.
при r = а, получим:
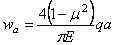 .
.
Отношение
перемещений двух характерных точек
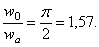
Перемещение
точек, лежащих внутри загруженного круга, но не в центре его, могут быть вычислены на основании (2.48) с помощью таблиц аллиптических интегралов.
б) Загрузка
на площади круга по “полушару”. Рассмотрим
случай, когда на площади круга радиуса а расположена нагрузка в виде
шапки (рис. 25) таким образом, что в любой точке загруженной территории
интенсивность нагрузки
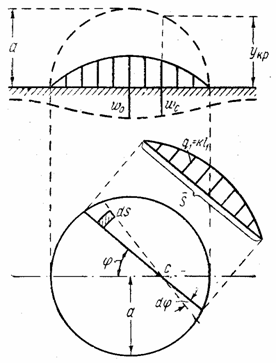
Рис. 25
пропорциональна
ординате полусферы, имеющей радиус а
и основанием которой служит упомянутая площадь круга. Иначе говоря, интенсивность
нагрузки в любой точке согласно обозначениям рис. 24 записывается так:
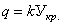 ;
;
здесь Укр. -
ордината круга, имеющего радиус a, k - коэффициент нагрузки, т. е.
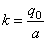 ,
,
a q0
- наибольшая
интенсивность нагрузки (т. е. в центре загруженной территории), причем q0
может быть выражена через общий вес:
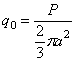 .
.
Для вычисления
перемещения точки С,
поступая аналогично предыдущему примеру, имеем:
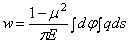 .
.
Выясним
геометрический смысл последнего интеграла. Из рассмотрения рис. 25 следует, что
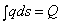 ,
,
где Q - площадь эпюры
нагрузки на длине 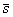 . Но так как, рассекая сферу любой плоскостью, мы всегда в
разрезе будем получать круг, то и в данном случае, рассекая нагрузку, в общем
изображаемую “полушаром”, мы всегда в разрезе должны
получить “полукруг” (этой фигурой в разрезе будет полуэллипс).
Таким образом, можем записать
. Но так как, рассекая сферу любой плоскостью, мы всегда в
разрезе будем получать круг, то и в данном случае, рассекая нагрузку, в общем
изображаемую “полушаром”, мы всегда в разрезе должны
получить “полукруг” (этой фигурой в разрезе будет полуэллипс).
Таким образом, можем записать
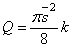 ,
,
где k - коэффициент,
позволяющий перейти от геометрического полукруга к “полукругу” в кавычках.
Итак,
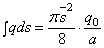
или, на
основании (2.47),
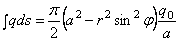 .
.
Теперь для
полного перемещения точки С
имеем:
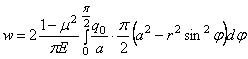 .
.
После
интегрирования получаем:
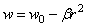 ,
(2.49)
,
(2.49)
где обозначено
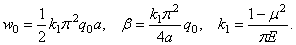
Если радиус
изогнутой поверхности граничной плоскости будет велик по сравнению с радиусом
загруженного круга, то выражение (2.49) можно практически считать уравнением
некоторой сферической поверхности.
в) Обратная
задача. Очевидно, можно решать и обратные задачи, когда задано уравнение
изогнутой "дневной" поверхности и требуется найти уравнение
нагрузки, вызвавшей такую деформацию.
Возьмем, например,
абсолютно жесткий штамп в виде круглого цилиндра, вдавливаемого в плоскую грань
упругого полупространства. В этом случае перемещение w для всех точек будет постоянным
по круглой подошве штампа; распределение давлений не будет постоянным и должно
определяться в результате решения интегрального уравнения
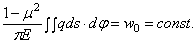
Решение такого
уравнения приводит к результату:
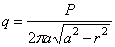 ,
,
где Р - полная нагрузка на
штамп, а - радиус
штампа и r -
радиус круга, на который действует давление q. Это распределение неравномерно и
наименьшее его значение в центре (r = 0), где
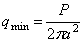 ,
,
т.е.
наименьшее давление равно половине среднего давления по круговой площади
подошвы штампа. На контуре этой площади (r = a)
давление становится бесконечно большим.
Перемещение
штампа выразится формулой
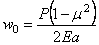 .
.
Если
предположить, что края штампа имеют некоторое закругление, как это показано на
рис.26, то распределение напряжений у краев штампов может существенно измениться.
Такая сложная контактная задача была поставлена И. Я. Штаерманом и привела к ответу, представленному графиком
на рис. 26.
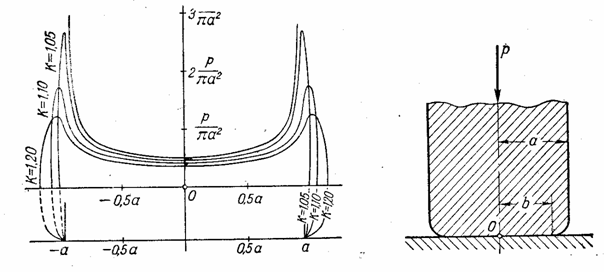
Рис. 26
В частности, это решение свободно
от бесконечно больших напряжений, не имеющих реального значения. На указанном
графике 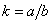 .
.
2.5 Вдавливание абсолютно
жесткого шара в упругое полупространство
Представим,
что на упругом полуространстве
покоится жесткий шар радиуса R (рис. 27).
Если нет давления
на этот шар
и исключить влияние собственного веса, то касание шара с
граничной плоскостью полупространства будет в точке. На расстоянии от точки
касания, малом по сравнению с R, зазор между шаром и граничной плоскостью может
быть, как известно, с достаточным приближением определен формулой:
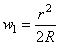 .
.
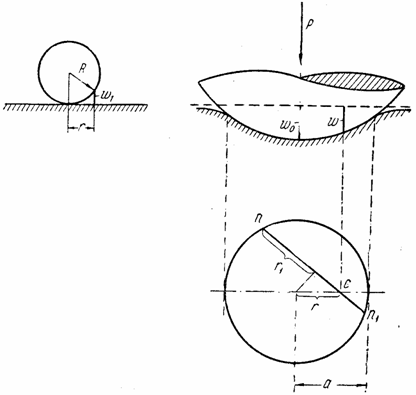
Рис. 27
Если к шару
будет приложена нагрузка, нормальная к первоначальной граничной плоскости и
проходящая через дентр шара, то вследствие упругости
полупространства граничная плоскость изогнется и шар опустится, как это показано
на рис. 26 (справа).
Ввиду
симметрии деформации относительно оси, совпадающей с направлением силы,
площадка контакта шара с деформированной граничной поверхностью упругого
полупространства будет представлять в плане круг некоторого радиуса а;
закон распределения давления под шаром не известен, (подлежит определению).
Очевидно, эпюра этого давления должна представлять фигуру, симметричную
относительно оси, совпадающей с силой.
Проведя через
точку С в плане бесконечно близкие секущие,
вычислим нагрузку, приходящуюся на бесконечно малую площадку dp,
отстоящую на расстоянии s
от точки С. Если напряжение смятия у этой площадки обозначим через q, то элементарная сила
на площадке dF соответствует
(2.45). Влияние этой силы на опускание точки Е определится, согласно
(2.45), таким образом:
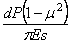
или, после
подстановки (2.46),
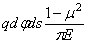 .
.
Влияние на
прогиб рассматриваемой точки С всех
элементарных давлений со всей площади контакта шара и упругого
полупространства оценится интегралом:
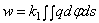 ,
(2.50)
,
(2.50)
В выражении
(2.50) неизвестными являются w
и функция распределения давления q. С другой стороны, из чисто геометрических соображений,
поскольку шар не деформируется, следует (рис. 27) что
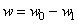 ,
(2.51)
,
(2.51)
где w0 - опускание шара (и
одновременно “прогиб” полупространства) в центре касания, a w1 - первоначальный
зазор между шаром и граничной плоскостью. Тогда исследуемый прогиб
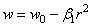 ,
(2.52)
,
(2.52)
где введено
обозначение:
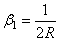 .
.
Уравнение
(2.51) выражает условие, что "упругая" поверхность полупространства представляет
под шаром часть поверхности этого шара. Объединяя (2.50) и (2.52), имеем:
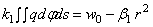 . (2.53)
. (2.53)
В выражении
(2.53) неизвестная функция q
входит под знак интеграла и, следовательно, (2.53) является интегральным
уравнением. Но именно такое же уравнение имелось и выше, где, наоборот, была
известна нагрузка (она была задана по “полушару”), а определялся характер изгиба граничной
плоскости.
На основании
сходства правых частей (2.53) и (2.49) заключаем, что эпюра распределения
давления по площади контакта представляет “полушар”.
Таким образом, если давление в центре контакта обозначим через q0, то на
расстоянии r от
этого центра давление
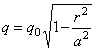 ,
,
а при r = а (на контуре круга касания) обращается в
нуль.
Все выражения
предыдущего раздела целиком относятся и к данной задаче, т. е.
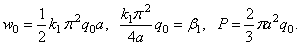 (2.54)
(2.54)
Решая (2.54)
относительно а, q0
и w0 ,
имеем:
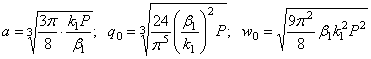 . (2.55)
. (2.55)
2.6. Задача об упругом смятии шаров
Представим,
что абсолютно жесткий шар радиуса R1 покоится на упругом теле сферической формы,
имеющей очень большой радиус R2,
и в дальнейшем подвергается действию силы Р
(рис. 28). При вычислении глубины вдавливания радиуса площадки
контакта и наибольшего напряжения смятия под указанным шаром можно
использовать формулы (2.55), введя вместо прежнего 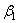 новое значение
новое значение 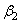 , определяемое выражением:
, определяемое выражением:
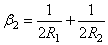 .
.
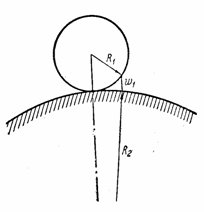
Рис. 28
Последнее вытекает из зависимости, составляемой для
выбираемого первоначального зазора w1 в случае касания двух сферических тел (рис.
28), и в данном случае имеем:
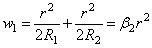 .
.
Таким образом,
при вдавливании жесткого шара в “почти бесконечную” сферу, получаем
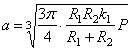 ;
(2.56)
;
(2.56)
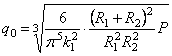 ; (2.57)
; (2.57)
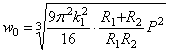 .
(2.58)
.
(2.58)
Полученные
формулы могут употребляться лишь в случае, если радиус площадки смятия а будет весьма малым по сравнению с
радиусом сферы R2,
вследствие чего последнюю можно при небольших размерах вдавливаемого шара
считать “полубесконечным” телом, закон деформации
которого был положен в основание вывода формул (2.55).
Если теперь
представить случай двух упругих “почти бесконечных” сфер, взаимно вдавливаемых
силами Р (рис. 29), т. е. верхнюю сферу считать
не абсолютно жесткой, а способной деформироваться, то
в этом случае
можно
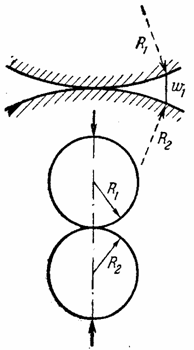
Рис. 29
воспользоваться
выводами предыдущей задачи, если ввести изменение в коэффициент, зависящий от
упругих свойств материалов, т. е. вместо k1 подставить
k = k1 + k2 ,
(2.59)
где
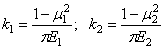 ,
,
Е1 и 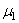 -
упругие характеристики материала верхней сферы; E2 и
-
упругие характеристики материала верхней сферы; E2 и 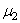 то же для нижней
сферы.
то же для нижней
сферы.
Возможность
такого простого перехода от формул (2.56), (2.57), (2.58) вытекает из тех
соображений, что в данной задаче ввиду деформаций обеих сфер исходное уравнение
деформации (2.53) должно быть записано в
виде:
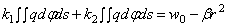 .
.
Последнее после введения обозначения (2.59), приводится к
виду (2.53) с заменой k1
и k2.
Так как при
сжатии упругих шаров радиус площадки смятия оказывается очень малым по
сравнению с радиусами самих шаров, то рассмотренная сейчас задача о сжатии
двух “почти бесконечных” сфер может быть практически использована и в задаче
об упругом сжатии шаров (задача Герца). Итак, при сжатии шаров имеем:
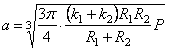 ; (2.60)
; (2.60)
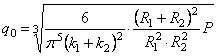 ; (2.61)
; (2.61)
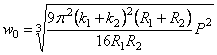 . (2.62)
. (2.62)
Зная закон
распределения давления по поверхности контакта, можно перейти к вычислению
напряжений внутри шаров, используя для этой цели (2.42) и применяя принцип
наложения.
Большой
практический интерес представляет нахождение внутри сжимаемых шаров точек,
имеющих большие касательные напряжения. Исследование этого вопроса приводит к
выводу, что точка, где касательное напряжение является наибольшим, лежит на оси
z на глубине,
равной примерно половине радиуса поверхности касания. Такую точку и следует
рассматривать как самую опасную (в свете третьей теории прочности) для таких
пластичных материалов, как сталь. Наибольшее касательное напряжение в этой
точке (при 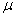 = 0,3) составляет примерно 0,31q0.
= 0,3) составляет примерно 0,31q0.
Из (2.60),
(2.61), (2.62) следует, что радиус площадки смятия, взаимное вдавливание и
напряжения смятия не находятся в линейной зависимости от силы Р. При
увеличении силы Р напряжения и
деформации шаров возрастают медленнее, чем возрастает сила.
Таким образом,
в контактной задаче принятие в основу исследования линейной связи между
компонентами напряжений и компонентами деформации в каждой точке упругого тела
(обобщенный закон Гука) повлекло за собой нелинейную зависимость между
силой и перемещениями.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
![]() .
.
![]() и
и ![]() , касательные — через
, касательные — через ![]() и
и ![]() . Эти напряжения надо считать функциями от z и r.
. Эти напряжения надо считать функциями от z и r.
![]()
![]()
![]() статические уравнения
запишутся:
статические уравнения
запишутся: (2.1)
(2.1)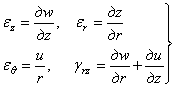 . (2.2)
. (2.2)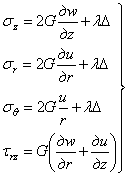 .
(2.3)
.
(2.3)![]()
![]() ,
(2.4)
,
(2.4)![]() надо понимать
обозначение следующей операции:
надо понимать
обозначение следующей операции:![]() .
. ![]() (2.5)
(2.5)![]() . (2.6)
. (2.6)![]() , положив
, положив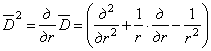 ,
,![]() из (2.6), получим:
из (2.6), получим:![]() . (2.7)
. (2.7)![]() , а затем вставить
, а затем вставить ![]() из уравнения (2.5):
из уравнения (2.5):![]() . (2.8)
. (2.8)![]() и
и ![]() через
через
![]() и
и ![]() по известным формулам
перехода
по известным формулам
перехода![]() ;
; ![]()
![]() ,
,![]() и
и ![]() не зависят от угла
не зависят от угла ![]() ,
тогда как
,
тогда как ![]() и
и ![]() являются функциями
являются функциями ![]() .
. , (2.9)
, (2.9)![]() .
(2.10)
.
(2.10) , (2.11)
, (2.11)![]() - произвольная
функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно
обратится в тождество. Второе уравнение равновесия и все уравнения
неразрывности будут удовлетворены, если принять
- произвольная
функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно
обратится в тождество. Второе уравнение равновесия и все уравнения
неразрывности будут удовлетворены, если принять ![]() согласно уравнению
согласно уравнению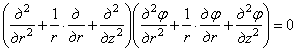 . (2.12)
. (2.12)![]() (2.13)
(2.13)![]() .
(2.14)
.
(2.14)![]() удовлетворяют
уравнению (2.12) при любых значениях коэффициентов С,
следовательно, любой член их также удовлетворяет уравнению (2.12). Например,
может быть
удовлетворяют
уравнению (2.12) при любых значениях коэффициентов С,
следовательно, любой член их также удовлетворяет уравнению (2.12). Например,
может быть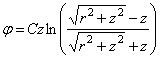 .
(2.15)
.
(2.15)![]() (2.16)
(2.16)![]() (2.17)
(2.17)![]() (2.18)
(2.18)![]() .
. ![]() отсутствует,
относительное удлинение по направлению оси z следует считать постоянным, т. е.
отсутствует,
относительное удлинение по направлению оси z следует считать постоянным, т. е.![]() (2.19)
(2.19)![]() .
(2.20)
.
(2.20)
![]() . (2.21)
. (2.21)![]() . (2.22)
. (2.22)![]() .
(2.23)
.
(2.23)![]() - переменная
интегрирования.
- переменная
интегрирования.![]() использовать граничные
уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то,
следовательно:
использовать граничные
уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то,
следовательно:![]()
![]()
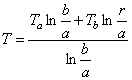 .
(2.24)
.
(2.24) (2.25)
(2.25) . (2.26)
. (2.26) 
![]() ,
, ![]() ) и радиальными (
) и радиальными (![]() ) напряжениями. Так как в рассматриваемом случае напряжения
зависят только от радиуса r, то
напряжения по двум бесконечно близким друг к другу концентрическим поверхностям
будут отличаться на величину
) напряжениями. Так как в рассматриваемом случае напряжения
зависят только от радиуса r, то
напряжения по двум бесконечно близким друг к другу концентрическим поверхностям
будут отличаться на величину ![]() и не будут
зависеть от угла
и не будут
зависеть от угла ![]() -
другого параметра, определяющего местоположение рассматриваемого элемента.
Проектируя все силы на нормаль к элементу, имеем уравнение равновесия в виде:
-
другого параметра, определяющего местоположение рассматриваемого элемента.
Проектируя все силы на нормаль к элементу, имеем уравнение равновесия в виде:![]() .
.![]() и производя
сокращения, получаем уравнение равновесия:
и производя
сокращения, получаем уравнение равновесия:![]() . (2.27)
. (2.27)![]() , (2.28)
, (2.28)![]() . (2.29)
. (2.29)
![]() и
и ![]() ) так:
) так: . (2.30)
. (2.30)![]() (2.31)
(2.31)![]() (2.32)
(2.32)![]() , (2.33)
, (2.33)![]() .
(2.34)
.
(2.34)![]() . (2.35)
. (2.35)![]() (2.36)
(2.36)![]() . (2.37)
. (2.37)![]() .
.![]()
![]()


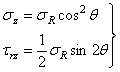
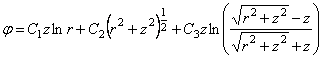

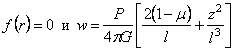


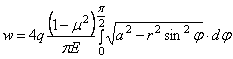

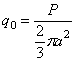
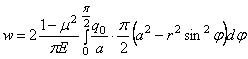


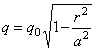
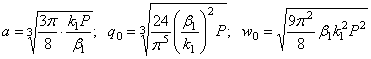 .
.
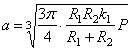
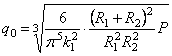
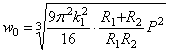 .
.