Главная

Лекция 1. Основы теории упругости

1.1 Основные положения, допущения и обозначения

Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть проверены решения, полученные с использованием допущений сопротивления материалов, и установлены границы применимости этих решений. Иногда разделы теории упругости, в которых, как и в сопротивлении материалов, рассматривается вопрос о пригодности детали, но с использованием достаточно сложного математического аппарата (расчет пластин, оболочек, массивов), относят к прикладной теории упругости.

В настоящей главе изложены основные понятия математической линейной теории упругости. Применение математики к описанию физических явлений требует их схематизации. В математической теории упругости задачи решаются с возможно меньшим числом допущений, что усложняет математические приемы, применяемые для решения. В линейной теории упругости предполагается существование линейной зависимости между составляющими напряжениями и деформациями. Для ряда материалов (резина, некоторые сорта чугуна) такая зависимость даже при малых деформациях не может быть принята: диаграмма s - e в пределах упругости имеет одинаковые очертания как при нагружении, так и при разгрузке, но в обоих случаях криволинейна. При исследовании таких материалов необходимо пользоваться зависимостями нелинейной теории упругости.

В математической линейной теории упругости исходят из следующих допущений:

1. О непрерывности (сплошности) среды. При этом атомистическая структура вещества или наличие каких-либо пустот не учитывается.

2. О естественном состоянии, на основании которого начальное напряженное (деформированное) состояние тела, возникшее до приложения силовых воздействий, не учитывается, т. е. предполагается, что в момент нагружения тела деформации и напряжения в любой его точке равны нулю. При наличии начальных напряжений это допущение будет справедливым, если только к результирующим напряжениям (сумме начальных и возникших от них из воздействий) могут быть применены зависимости линейной теории упругости.

3. Об однородности, на основании которого предполагается, что состав тела одинаков во всех точках. Если применительно к металлам это допущение не дает больших погрешностей, то в отношении бетона при рассмотрении малых объемов оно может привести к значительным погрешностям.

4. О шаровой изотропности, на основании которого считается, что механические свойства материала одинаковы по всем направлениям. Кристаллы металла не обладают таким свойством, но для металла в целом, состоящего из большого числа мелких кристаллов, можно считать, что эта гипотеза справедлива. Для материалов, обладающих различными механическими свойствами в разных направлениях, как, например, для слоистых пластиков, разработана теория упругости ортотропных и анизотропных материалов.

5. Об идеальной упругости, на основании которого предполагается полное исчезновение деформации после снятия нагрузки. Как известно, в реальных телах при любом нагружении возникает остаточная деформация. Поэтому допущение следует считать применимым, если остаточная деформация не превышает условно заданной нормы.

6. О линейной зависимости между составляющими деформациями и напряжениями.

7. О малости деформаций, на основании которого предполагается, что относительные линейные и угловые деформации малы по сравнению с единицей. Для таких материалов, как резина, или таких элементов, как спиральные пружины, создана теория больших упругих деформаций.

При решении задач теории упругости пользуются теоремой о единственности решения: если заданные внешние поверхностные и объемные силы находятся в равновесии, им соответствует одна единственная система напряжений и перемещений. Положение о единственности решения справедливо, если только справедливы допущение о естественном состоянии тела (иначе возможно бесчисленное количество решений) и допущение о линейной зависимости между деформациями и внешними силами.

При решении задач теории упругости часто пользуются принципом Сен-Венана: если внешние силы, приложенные на небольшом участке упругого тела, заменить действующей на том же участке статически эквивалентной системой сил (имеющей тот же главный вектор и тот же главный момент), то эта замена вызовет лишь изменение местных деформаций.

В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения мало зависят от способа их приложения. Нагрузка, которая в курсе сопротивления материалов схематически выражалась на основании принципа Сен-Венана в виде силы или сосредоточенного момента, на самом деле представляет собой нормальные и касательные напряжения, распределенные тем или иным способом на определенном участке поверхности тела. При этом одной и той же силе или паре сил может соответствовать различное распределение напряжений. На основании принципа Сен-Венана можно считать, что изменение усилий на участке поверхности тела почти не отражается на напряжениях в точках, удаленных на достаточно большое расстояние от места приложения этих усилий (по сравнению с линейными размерами нагруженного участка).

Положение исследуемой площадки, выделенной в теле (рис. 1), определяется направляющими косинусами нормали N к площадке в выбранной системе прямоугольных осей координат х, у и z.

Если Р — равнодействующая внутренних сил, действующих по элементарной площадке , выделенной у точки А, то полное напряжение р_N в этой точке по площадке с нормалью N определяется как предел отношения в следующей форме:

.

Вектор р_N можно разложить в пространстве на три взаимно перпендикулярные составляющие.

а б

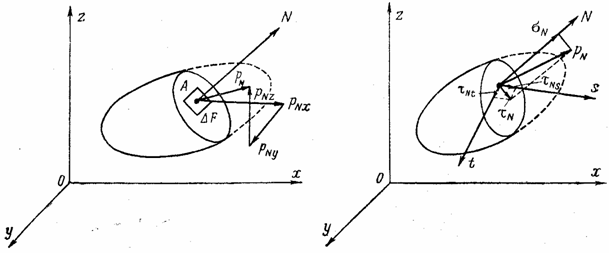
Рис. 1

1. На составляющие р_Nx , р_Ny и р_Nz по направлениям трех осей (рис. 1, а). Эти составляющие положительны, если совпадают по направлению с положительными направлениями соответствующих осей. Согласно рис. 1, а

. (1.1,а)

2. На составляющие , и по направлениям нормали к площадке (нормальное напряжение) и двух взаимно перпендикулярных осей s и t (рис. 1,б), лежащих в плоскости площадки (касательные напряжения). Согласно рис.1, б

. (1.1,б)

Если сечение тела или площадка параллельны одной из плоскостей координат, например у0z (рис. 2), то нормалью к этой площадке будет третья ось координат х и составляющие напряжения будут иметь обозначения , и .

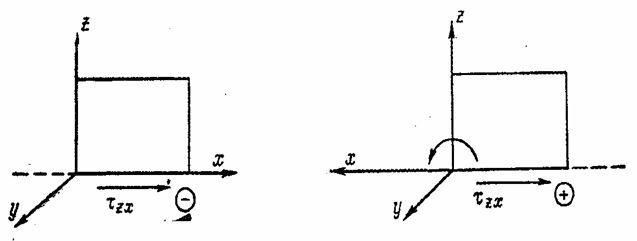
Нормальное напряжение положительно, если оно растягивающее, и отрицательно, если оно сжимающее. Знак касательного напряжения определяется с помощью следующего правила: если положительное (растягивающее) нормальное напряжение по площадке дает положительную проекцию, то касательное напряжение по той же площадке считается положительным при условии, что оно тоже дает положительную проекцию на соответствующую ось; если же растягивающее нормальное напряжение дает отрицательную проекцию, то положительное касательное напряжение тоже должно давать отрицательную проекцию на соответствующую ось.

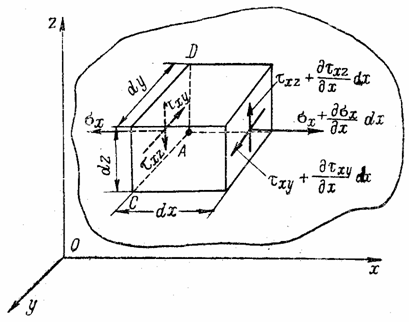
Рис. 2

На рис. 3, например, все составляющие напряжения, действующие по граням элементарного параллелепипеда, совпадающим с плоскостями координат, положительны.

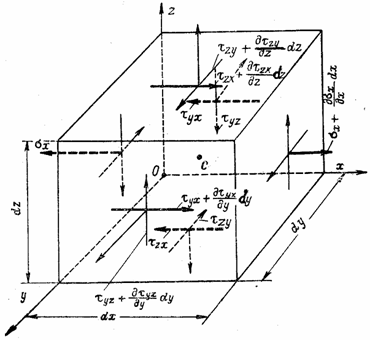
Рис. 3

Чтобы определить напряженное состояние в точке упругого тела, необходимо знать полные напряжения р_N по трем взаимно перпендикулярным площадкам, проходящим через эту точку. Так как каждое полное напряжение можно разложить на три составляющие, напряженное состояние будет определено, если будут известны девять составляющих напряжений. Эти составляющие можно записать в виде матрицы

,

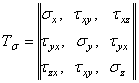называемой матрицей компонентов тензора напряжений в точке.

В каждой горизонтальной строчке матрицы записаны три составляющих напряжения, действующих по одной площадке, так как первые значки (название нормали) у них одинаковые. В каждом вертикальном столбце тензора записаны три напряжения, параллельных одной и той же оси, так как вторые значки (название оси, параллельно которой действует напряжение) у них одинаковые.

1.2 Уравнения равновесия элементарного параллелепипеда и элементарного тетраэдра

Выделим у исследуемой точки А (с координатами х, у и z) напряженного упругого тела тремя взаимно перпендикулярными парами плоскостей элементарный параллелепипед с размерами ребер dx, dy и dz (рис. 2). По каждой из трех взаимно перпендикулярных граней, примыкающих к точке А (ближайших к плоскостям координат), будут действовать три составляющих напряжения - нормальное и два касательных. Считаем, что по граням, примыкающим к точке А, они положительны.

При переходе от грани, проходящей через точку А, к параллельной грани напряжения меняются и получают приращения. Например, если по грани CAD, проходящей через точку А, действуют составляющие напряжения = f₁ (x,y,z), =f₂ (x,y,z,), =f₃ (x,y,z,), то по параллельной грани, вследствие приращения только одной координаты х при переходе от одной грани к другой, будут действовать составляющие напряжения Можно определить напряжения на всех гранях элементарного параллелепипеда, как показано на рис. 3.

Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, У и Z. Если приравнять нулю сумму проекций на ось х всех нормальных, касательных и объемной сил, действующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение

.

Составив аналогичные уравнения проекций сил на оси у и z, напишем три дифференциальных уравнения равновесия элементарного параллелепипеда, полученных Коши,

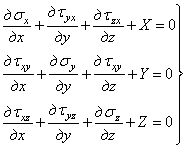. (1.2)

При уменьшении размеров параллелепипеда до нуля он превращается в точку, а и представляют собой составляющие напряжения по трем взаимно перпендикулярным площадкам, проходящим через точку А.

Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси x_c, параллельной оси х и проходящей через его центр тяжести, получим уравнение

или, с учетом того, что второй и четвертый члены уравнения высшего порядка малости по сравнению с остальными, после сокращения на dxdydz

или .

Составив аналогичные уравнения моментов относительно центральных осей у_c и z_c , получим три уравнения закона парности касательных напряжений

, , . (1.3)

Этот закон формулируется так: касательные напряжения, действующие по взаимно перпендикулярным площадкам и направленные перпендикулярно к линии пересечения площадок, равны по величине и одинаковы по знаку.

Таким образом, из девяти составляющих напряжений матрицы тензора шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следующие шесть составляющих напряжений:

.

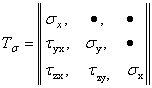Но составленные условия равновесия дали нам всего лишь три уравнения (1.2), из которых шесть неизвестных найдены быть не могут. Таким образом, прямая задача определения напряженного состояния в точке в общем случае статически неопределима. Для раскрытия этой статической неопределимости необходимы дополнительные геометрические и физические зависимости.

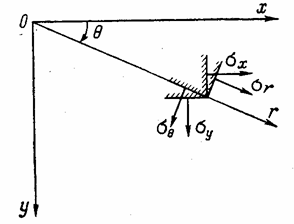
Рассечем элементарный параллелепипед у точки А плоскостью, наклоненной к его граням; пусть нормаль N к этой плоскости имеет направляющие косинусы l, т и п. Получившаяся геометрическая фигура (рис. 4) представляет собой пирамиду с треугольным основанием - элементарный тетраэдр. Будем считать, что точка А совпадает с началом координат, а три взаимно перпендикулярные грани тетраэдра - с плоскостями координат.

Составляющие напряжения, действующие по этим граням тетраэдра, будем считать положительными. Они показаны на рис. 4. Обозначим через и проекции полного напряжения p_N , действующего по наклонной грани BCD тетраэдра, на оси х, у и z. Площадь наклонной грани BCD обозначим dF. Тогда площадь грани АВС будет dF, грани ACD - dF и грани АDВ - dF .

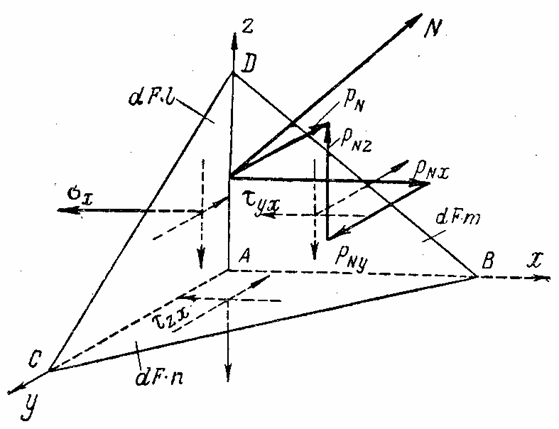
Рис. 4

Составим уравнение равновесия тетраэдра, спроектировав все силы, действующие по его граням, на ось х; проекция объемной силы в уравнение проекций не входит, так как представляет собой величину высшего порядка малости по сравнению с проекциями поверхностных сил:

,

откуда

.

Составив уравнения проекции сил, действующих на тетраэдр, на оси у и z, получим еще два аналогичных уравнения. В результате будем иметь три уравнения равновесия элементарного тетраэдра

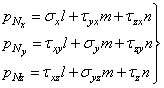. (1.4)

По известным трем проекциям найдем полное напряжение

. (1.5)

Разделим пространственное тело произвольной формы системой взаимно перпендикулярных плоскостей хОу, yОz и хОz (рис. 5) на ряд элементарных параллелепипедов. У поверхности тела при этом образуются элементарные тетраэдры, (криволинейные участки поверхности ввиду их малости можно заменить плоскостями). В таком случае р_N будет представлять нагрузку на поверхности, а уравнения (1.4) будут связывать эту нагрузку с напряжениями и в теле, т. е. будут представлять граничные условия задачи теории упругости. Условия, определяемые этими уравнениями, называют условиями на поверхности.

Рис. 5

Следует отметить, что в теории упругости внешние нагрузки представляются нормальными и касательными напряжениями, приложенными по какому-либо закону к площадкам, совпадающим с поверхностью тела.

1.3 Нормальные и касательные напряжения по наклонной площадке

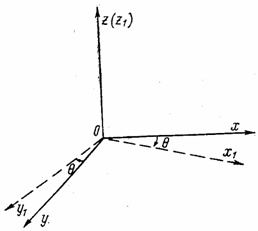
Рассмотрим элементарный тетраэдр ABCD, три грани которого параллельны координатным плоскостям, а нормаль N к четвертой грани составляет с координатными осями углы, косинусы которых равны l, т и п (рис. 6). Будем считать заданными составляющие нормальные и касательные напряжения, действующие по площадкам, лежащим в координатных плоскостях, и определим напряжения на площадке BCD. Выберем новую систему прямоугольных осей координат х₁ , y₁ и z₁, так чтобы ось х₁ совпадала с нормалью N , а оси у₁ и z₁ лежали в плоскости площадки BCD. Каждая из этих осей будет иметь в системе осей x, y, z свои направляющие косинусы, указанные в табл. 1.

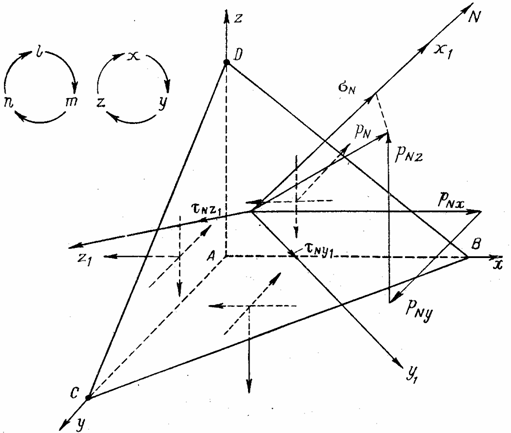
Рис. 6

Таблица 1

Оси	x	y	z
x1	l1	m1	n1
y1	l2	m2	n2
z1	l3	m3	n3

Полное напряжение р_N, действующее по площадке BCD, разложим на составляющие р_Nx , p_Ny и p_Nz . Нормальное напряжение действующее по площадке BCD, можно рассматривать как проекцию на ось N (или х₁) полного напряжения p_N , действующего по площадке BCD, а полное напряжение р_N - как равнодействующую трех его проекций. Так как проекция равнодействующей равна сумме проекций составляющих, то

.

Подставив выражения (1.4) и произведя необходимые сокращения, запишем

s_N = s_x l² + s_y m² + s_z n² + 2t_xy lm + 2t_yz mn + 2t_zx nl. (1.6)

Спроектировав составляющие р_Nx , p_Ny и p_Nz на ось у₁ (рис. 6), получим

,

а заменив их выражениями (1.4) и приведя подобные члены, -

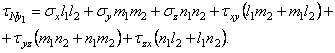(1.7,а)

Аналогично из суммы проекций на ось z₁ найдем выражение для третьего составляющего касательного напряжения

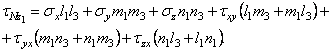(1.7,б)

С помощью формул (1.6) и (1.7) можно преобразовать составляющие тензора напряжений при переходе от одной системы координат х, у, z к новой системе координат х₁, у₁, z₁.

Для записи (1.6), (1.7) и ряда других формул теории упругости можно установить последовательность чередования индексов у составляющих напряжений и чередования направляющих косинусов, показанную схематически на рис. 6.

1.4 Определение главных напряжений и наибольших касательных напряжений в точке

В курсах математической теории упругости доказывается, что в любой точке тела можно найти три взаимно перпендикулярные главные площадки, на которых отсутствуют касательные напряжения. Нормальные напряжения по этим площадкам называются главными напряжениями. Одно из них представляет собой наибольшее напряжение в данной точке, другое ¾ наименьшее, а третье имеет величину, промежуточную между первыми двумя.

Предположим, что наклонная грань BCD тетраэдра, выделенного у точки А напряженного тела (рис. 7), — главная площадка. Обозначим направляющие косинусы нормали к главной площадке l, m и п. Полное напряжение р_v, действующее по главной площадке, направлено по нормали v и равно главному нормальному напряжению. Касательное напряжение равно нулю.

Составим по формулам (1.4) выражения для проекций напряжения р_v на оси координат:

.

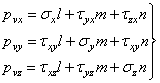С другой стороны, те же проекции p_vx = p_vl; p_vy = p_vm; p_vz = p_vn.

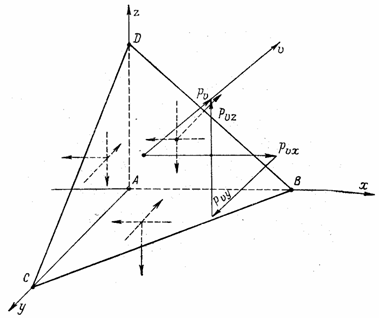
Рис. 7

Так как левые части в уравнениях равны, приравниваем правы части и получаем систему

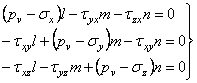, (1.8)

в которой четыре неизвестных: главное напряжение р_v и три направляющих косинуса. Четвертое недостающее уравнение системы — условие равенства единице суммы квадратов направляющих косинусов:

l² + m² + n² = 1. (1.9)

Из соотношения следует, что направляющие косинусы не могут все одновременно быть равны нулю, поэтому система уравнений с неизвестными l, т и п должна иметь решения, отличные от нуля, а значит ее определитель должен равняться нулю. Раскрыв этот определитель, получим

,

где введены обозначения

.

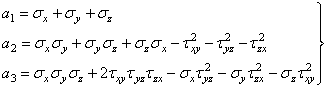Решив кубическое уравнение, получим три значения его корня, т. е. три главных напряжения, из которых алгебраически наибольшее назовем , наименьшее , а промежуточное . Величины главных напряжений в точке, не зависят от выбора осей координат, а зависят от формы и размеров тела и его нагружения. Следовательно, коэффициенты а₁ и а₂ и свободный член а₃ в этом уравнении также не должны зависеть от выбора осей координат. Поэтому функции а₁ и а₂ составляющих напряжений и свободный член а₃, называются инвариантами системы осей координат.

Так как число главных площадок равно трем, должно быть найдено девять направляющих косинусов. Чтобы найти, например, направляющие косинусы l₁ , т₁, п₁ нормали к площадке, по которой действует главное напряжение , надо подставить значение в какие-нибудь два уравнения (1.8).

Решив эти два уравнения, найдем значения двух направляющих косинусов, например l₁ и m₁ , выраженные через п₁. Подставив найденные значения l₁ и т₁ в уравнение (1.9), найдем третий направляющий косинус п₁ первой главной площадки.

Рассмотрим снова элементарный тетраэдр у точки А (рис. 8). Предположим, что три взаимно перпендикулярные его грани представляют собой главные площадки в точке А.

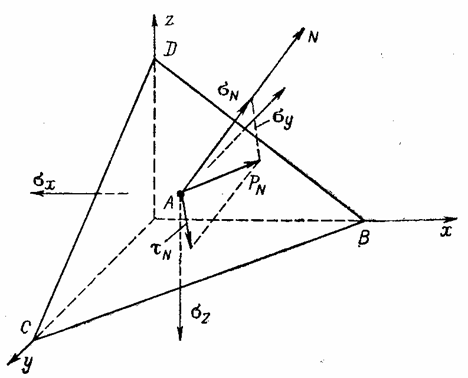
Рис. 8

Составим выражение для касательного напряжения t, действующего по наклонной грани BCD тетраэдра, имеющей направляющие косинусы l, т и n, и найдем экстремальные значения этого напряжения и положение площадок, по которым они действуют. На основании формулы (1.1,б) квадрат касательного напряжения по площадке BCD

.

Ввиду того, что грани тетраэдра ACD, ACВ и ABD — главные площадки, подстановка в это уравнение выражений для p_N , вычисленных по формулам (1.1,а), (1.4) и (1.6), дает

Из соотношения (1.9)

n² = 1 – l² – m²,

тогда

.

Наибольшее значение касательного напряжения t_N найдется из условий

,

дающих два уравнения с двумя неизвестными l и m.

Предположим, что обозначены соответственно , тогда последние два уравнения примут вид двух уравнений третьей степени относительно l и т

.

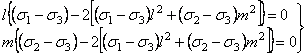Если отбросить не отвечающие исходным условиям задачи решения системы уравнений, останутся следующие значения двух групп направляющих косинусов:

Первая группа при положительных т и п определяет нормаль, лежащую в плоскости у0z и составляющую с этими осями углы в 45°, или площадку, делящую пополам прямой угол между главными площадками, по которым действуют напряжения и . При отрицательных т и п первая группа определяет нормаль и площадку соответственно перпендикулярные к первым (рис. 9, а).

а б

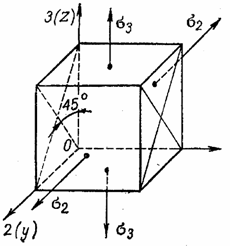
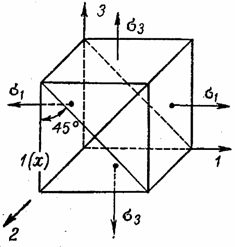
в

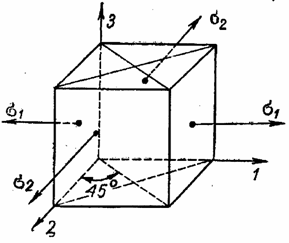
Рис. 9

Вторая группа определяет две площадки, делящие пополам прямые углы между главными площадками, по которым действуют и (рис. 9, б).

Можно получить новую систему кубических уравнений, из которой можно найти третью группу направляющих косинусов:

3)

определяющих еще две взаимно перпендикулярные площадки (рис. 9, в).

Таким образом, найдены три пары взаимно перпендикулярных площадок. По каждой из этих пар касательные напряжения одинаковы и представляют наибольшее напряжение для определенной группы площадок.

Величина трех наибольших касательных напряжений получается путем подстановки значений l, т и п первой, второй и третьей групп в уравнение для . Каждое из них равно полуразности двух главных напряжений:

(1.10)

1.5 Напряжения по октаэдрическим площадкам

Выделим у точки А площадками, равнонаклоненными к главным площадкам, элементарный октаэдр (рис. 10). При уменьшении размеров октаэдра его грани, лежащие в накрест расположенных четвертях, сольются, и мы получим четыре площадки, проходящие через точку А, называемые октаэдрическими.

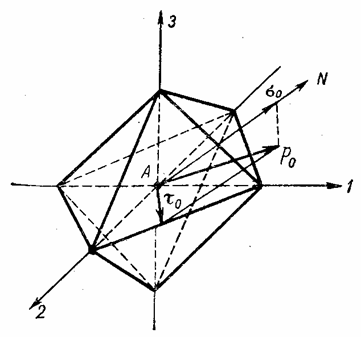
Рис. 10

Вычислим нормальные и касательные напряжения, действующие по октаэдрической площадке. Так как в главных осях 1, 2, 3 все три направляющих косинуса нормали к октаэдрической площадке одинаковы, а сумма их квадратов равна единице, то

(1.11)

Подставляя эти значения в формулу (1.6) и учитывая инвариантность суммы нормальных напряжений по трем взаимно перпендикулярным площадкам, находим нормальное напряжение по октаэдрической площадке

. (1.12)

Полное напряжение по октаэдрической площадке на основании формул (1.1,a) и (1.4)

.

Касательное напряжение по октаэдрической площадке

.

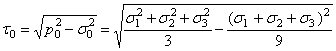Приведя подкоренное выражение к общему знаменателю, найдем

, (1.13)

или, с учетом выражения (1.10),

. (1.13,а)

1.6 Понятие о перемещениях. Зависимости между деформациями и перемещениями

Предположим, что упругое тело закреплено и не может перемещаться в пространстве. Тогда его точки могут изменять положение в пространстве только за счет деформации тела.

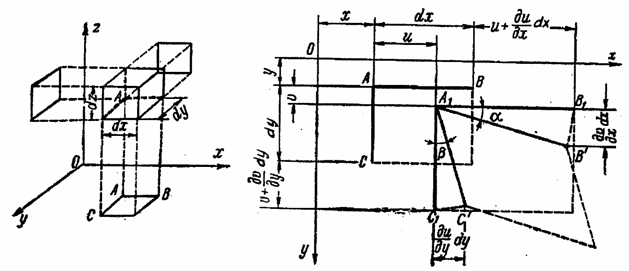
Пусть какая - нибудь точка А упругого тела (рис. 11), имевшая до деформации координаты х, у и z, вследствие деформации тела оказалась в положении A₁ с координатами х + и, у + v и z + w. Отрезок AA₁ называется линейным перемещением точки A, а отрезки и, v и w — проекциями этого перемещения на оси координат. Перемещения и их проекции для разных точек различны; они представляют собой непрерывные (по условиям сплошности) функции координат точки:

u =f₁ (x, y, z); v = f₂ (x, y, z); w = f₃ (x, y, z).

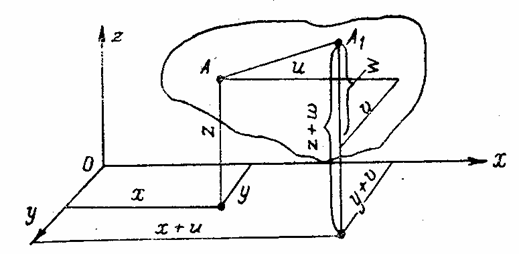
Рис. 11

Деформированное состояние в точке А (рис. 12, а) будет известно, если будут известны деформации всех трех проекций элементарного параллелепипеда. Для этого надо знать: относительные линейные деформации трех взаимно перпендикулярных ребер , и и изменения прямых углов между ребрами в плоскостях трех его граней, параллельных плоскостяx координат (относительные сдвиги или относительные угловые деформации , , .

а	б

Рис. 12

Относительное изменение объема элементарного параллелепипеда при деформации

Если отбросить величины второго и третьего порядка малости,

, (1.14)

где средняя относительная линейная деформация

.

Найдем зависимости между составляющими деформациями и проекциями перемещения на оси координат. Для этого рассмотрим проекцию элементарного параллелепипеда на плоскость хОу. Пусть заданы первоначальные координаты точки А — х и у и длины проекций ребер dx и dy (рис. 12, б). После деформации тела точка А перейдет в положение A₁ , а точка В — в положение В₁.

Линейное перемещение точки В вдоль оси х равно сумме линейного перемещения точки А и его приращения, вызванного изменением координаты х при переходе от точки А к точке В. Это приращение равно частному дифференциалу функции и = f₁ (x, y, z) по переменной х. Поэтому линейное перемещение точки В равно . Кроме того, вследствие изменения первоначального прямого угла ВАС на величину точка В₁ займет положение В'. Отрезок В₁В' представляет изменение перемещения v точки А при переходе от точки А к точке В вдоль оси х.

Относительная деформация ребра АВ

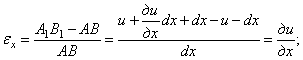
аналогично найдем

Изменение прямого угла ВАС в плоскости хОу получим, заменив углы и их тангенсами,

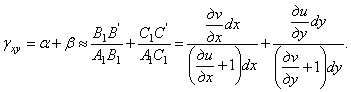
Если пренебречь в скобках частными производными, которые малы по сравнению с единицей, то

Из проекций элементарного параллелепипеда на две другие плоскости координат найдем выражение для относительной линейной деформации и относительных сдвигов и . В результате получим следующие шест зависимостей между относительными деформациями и перемещениями:

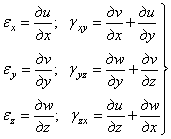. (1.15)

Зависимости (1.15) получены Коши. Исходя из геометрического смысла частных производных, стоящих в правой части, можно установить правила знаков: положительное значение относительных линейных деформаций соответствует удлинению, положительное значение относительных сдвигов соответствует уменьшению прямых углов хОу, уОz и zОx.

1.7 Относительная линейная деформация в произвольном направлении

Наметим внутри упругого тела две точки А (х, у, z) и В (х + dx, у + dy, z + dz), находящиеся на расстоянии dr друг от друга (рис. 13). Направляющие косинусы отрезка dr обозначим l, т и п.

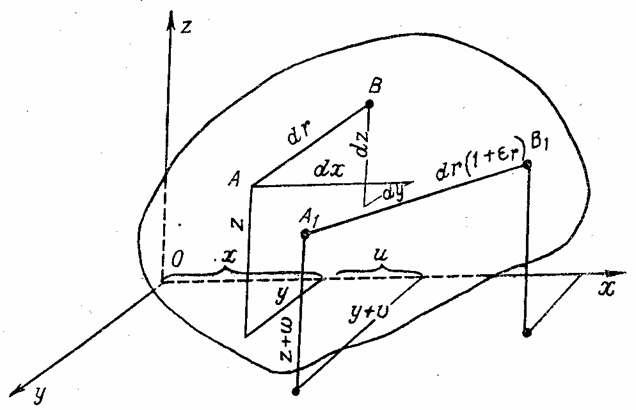
Рис. 13

При деформации тела под влиянием внешней нагрузки, точка А перейдет в положение А₁, точка В в положение В₁, а отрезок dr получит приращение . Новая длина отрезка АВ

,

где – искомая относительная линейная деформация.

Проекции перемещения АА₁ точки А на оси координат обозначаем и, v и w. Тогда проекции перемещения ВВ₁ точки В на оси координат и + du, v + dv, w + dw.

С одной стороны

.

С другой стороны, квадрат отрезка А₁В₁ равен сумме квадратов трех его проекций на оси координат:

(А₁В₁)² = dx² + dy² + dz² + 2dxdu + 2dydv + 2dzdw.

Тогда получим

.

Подставив выражения для полных дифференциалов перемещений и, v и w, и заметив, что

учитывая, что l² + m² + п² = 1, сокращая на 2, и используя зависимости (1.15), получаем

. (1.16)

Сравнение выражений (1.16) для линейной деформаций , и (1.6) для нормального напряжения в том же направлении, показывает, что они по структуре одинаковы и выражение (1.16) может быть получено из формулы (1.6) путем замены с сохранением значков на и на . Пользуясь такой заменой, можно получить все формулы теории деформации из аналогичных формул теории напряжений. В частности, деформированное состояние в точке упругого тела определяется матрицей компонентов тензора деформаций:

.

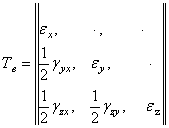1.8. Уравнения совместности деформаций

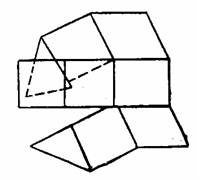
Из уравнений (1.15) видно, что если заданы три функции и, v и w, то все шесть составляющих деформаций будут определены однозначно. Но задать эти шесть составляющих произвольно нельзя. Они должны быть связаны дополнительными зависимостями — уравнениями совместности.

Из допущения о сплошности тела следует, что перемещения в его точках должны представлять собой непрерывные и однозначные функции от координат. Для таких функций величина их производных не зависит от порядка дифференцирования. Поэтому, если дифференцировать по различным переменным координатам уравнения перемещений, после математических преобразований можно получить искомые зависимости между составляющими относительных линейных и угловых деформаций. Так как эти зависимости связаны с условиями сплошности тел, они называются также уравнениями неразрывности.

Если эти уравнения не соблюдены, то из малых параллелепипедов и тетраэдров, на которые можно разделить упругое тело (рис. 14,а), после деформации каждого из них, зависящей от шести составляющих (рис. 14,б), может оказаться невозможным сложить непрерывное деформированное тело (рис. 14, в).

а	б	в

Рис. 14

Дифференцируя первые два уравнения (1.15) для линейных деформаций, находим

.

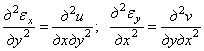Складывая эти выражения и учитывая выражение для угловой деформации , получаем

.

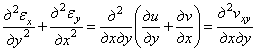Произведя круговую подстановку индексов, можно получить еще два аналогичных уравнения, которые составят первую группу уравнений неразрывности

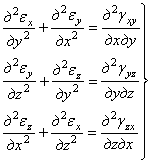. (1.17,а)

Дифференцируем уравнения для угловых деформаций (1.15), складываем первые два уравнения и вычитаем третье:

.

Дифференцируем это уравнение по у:

.

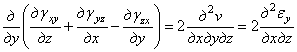После круговой подстановки можно получить еще два аналогичных уравнения, которые составят вторую группу уравнений неразрывности

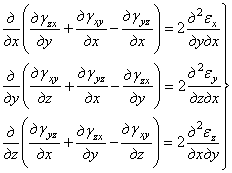. (1.17,б)

Шесть условий (1.17,а) и (1.17,6) будут удовлетворены, если при решении задачи теории упругости удастся по заданным нагрузкам, действующим на тело, найти выражения для и, v и w. Если затем вычислить деформации по уравнениям (1.15), то уравнения совместности, превратятся в тождества, так как они выведены из тех же уравнений (1.15).

Если же при решении задачи по нагрузкам найдем напряжения, а затем деформации, необходимо проверить, удовлетворяют ли найденные деформации уравнениям совместности.

Можно доказать, что уравнения совместности представляют собой необходимые условия для того, чтобы по уравнениям (1.15) можно было найти составляющие перемещения по заданным составляющим деформациям.

Таким образом, зависимости (1.17,а и 17,б) являются необходимыми и достаточными условиями интегрируемости формул (1.15), обеспечивающими одновременно однозначность перемещений. Это справедливо, если тело ограничено односвязной областью, т. е. областью, в пределах которой любая замкнутая кривая может быть непрерывной деформацией стянута в точку без пересечения контура области.

1.9 Закон Гука для изотропного тела

Опытами установлено, что для упругих тел при напряжениях меньше предела упругости компоненты матрицы тензора деформаций Т_е представляют собой линейные функции составляющих тензора напряжений. Они могут быть в общем случае представлены следующими линейными уравнениями:

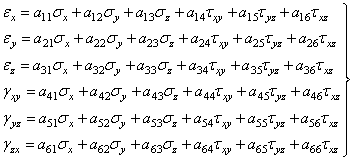. (1.18)

Можно доказать, что для системы линейных уравнений (1.18) коэффициенты, расположенные симметрично относительно главной диагонали, должны быть равны: a_nm = a_mn. Поэтому в этих уравнениях отпадает (36-6)/2=15 коэффициентов и остается 36 – 15 = 21.

Коэффициенты а₁₁, . . ., а₆₆, число которых 21, зависят от свойств материала и представляют собой упругие постоянные любого анизотропного материала, обладающего различными упругими свойствами в различных направлениях.

Для тела из однородного изотропного упругого материала число произвольных постоянных может быть сокращено. Можно считать, что линейные деформации у этих материалов зависят только от нормальных напряжений, а угловые – только от касательных. Вследствие этого уравнения (1.18) разобьются на две системы из трех уравнений, каждая из которых содержит три неизвестных. Всего останется 18 коэффициентов:

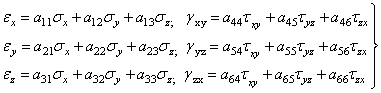. (1.18,а)

Коэффициенты, расположенные симметрично относительно главных диагоналей, равны друг другу. Поэтому отпадает 2(9-3)/2=6 коэффициентов и остается 18 - 6 = 12.

При заданных напряжениях и деформации и не должны зависеть от выбора осей координат. Это будет соблюдаться, если еще ряд коэффициентов будет равен нулю. Например, при показанном на рис. 15,а направлении касательного напряжения оно отрицательно. Если же направление оси х изменить на обратное, (рис. 15,б), знак напряжения станет положительным и равенство между левой и правой частями четвертого уравнения (1.18а) нарушится. Этого не будет лишь в случае, когда a₄₆ = 0; a₆₄ = 0.

а	б

Рис. 15

Если повернуть таким же образом ось у, а затем ось z, можно установить, что

a₄₅ = a₅₄ = 0 и а₅₆ = а₆₅ = 0.

Если повернуть одновременно оси х и у по часовой стрелке на 90°, т. е. заменить ось Оу на Ох, а ось Ох на Оу, то в первом уравнении (1.18,а) напряженияи поменяются местами. При этом равенство между левой и правой частями не нарушится лишь при условии а₁₁ = а₁₃. Аналогично во втором и третьем уравнениях (1.18,а) должно быть а₂₁ = а₂₂ и а₃₁ = а₃₂.

Если повернуть другие оси, т. е. заменить ось Оу на Оz, затем ось Оz на Ох, можно найти еще равенства

a₁₁ = a₂₂ = a₃₃ и а₄₄ = а₅₅ = а₆₆.

В результате число постоянных для изотропного тела сокращается до трех, известных из курса сопротивления материалов. Из них только две независимы.

Независимыми упругими постоянными могут быть любые две из следующих четырех величин: модуль продольной упругости Е, модуль сдвига G, объемный модуль упругости k и коэффициент поперечной деформации (коэффициент Пуассона) . Они связаны между собой линейной зависимостью

, (1.19)

а также зависимостью (1.22).

Уравнения, связывающие составляющие тензора деформаций и составляющие тензора напряжений (закон Гука) для однородного изотропного упругого материала, могут быть представлены следующим образом:

1. Известными из курса сопротивления материалов выражениями для составляющих деформаций

. (1.20)

2. Выражением, связывающим объемные характеристики. Для этого к первому из уравнений (1.20) прибавим в скобках и , ко второму и и к третьему и . Сложим все три уравнения и, с учетом формул (1.12) и (1.14), получим

или

, (1.21)

где

(1.22)

называется объемным модулем упругости.

1. Уравнениями, решенными относительно составляющих напряжений. Для этого первое уравнение (1.20) представим, использовав формулу (1.21), в виде

.

Решив это уравнение относительно с учетом формулы (1.19), найдем

где

(1.23)

представляют собой величины, зависящие только от упругих постоянных Е и материала, и называются коэффициентами Ламе.

Таким же преобразованием двух следующих уравнений (1.20) получим выражения для и , а решением трех последних уравнений (1.20) - выражения для . Итак:

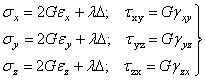. (1.24)

1.10 Плоская задача в прямоугольных координатах

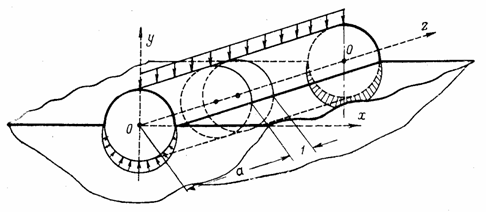
Большая категория задач теории упругости допускает значительное упрощение математического решения. Это задачи, в которых можно считать, что внешние воздействия лежат в плоскостях, параллельных какой-либо плоскости хОу, и что вызываемые ими напряжения и перемещения одинаковы для всех точек любой оси z, перпендикулярной этой плоскости. Напряжения по площадкам хОу и перемещения по направлению оси z или отсутствуют, или представляют собой функции напряжений и перемещений, возникающих в плоскости хОу. Такие задачи объединяются общим названием — плоские задачи. Различают две разновидности плоской задачи: плоское деформированное и плоское напряженное состояния.

При плоском деформированном состоянии точки тела не могут перемещаться вдоль оси z (рис.16,а) из-за препятствия со стороны соседних элементов (вдали от торцов при большой длине тела). Нагрузка, действующая на тело, постоянна вдоль оси z, но может меняться в плоскости хОу при условии, что она в этой плоскости уравновешена. В таком случае любой элемент толщиной, равной единице, вырезанный двумя параллельными сечениями, перпендикулярными оси z, на известном расстоянии z = а от торцов (рис. 16,б) находится в одинаковых условиях с соседними и испытывает плоское деформированное состояние. Перемещения w вдоль оси z отсутствуют (w = 0), а два других (и и v) не зависят от координаты z.

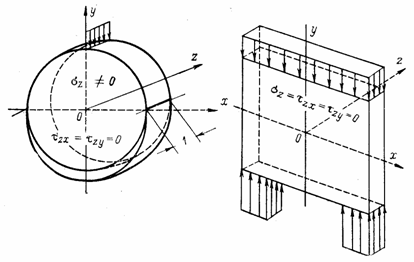
При плоском напряженном состоянии размеры тела вдоль оси z малы (рис. в), а боковые плоскости хОу свободны от нагрузки, т.е. напряжения , и этим плоскостям равны нулю. Ввиду малой толщины можно предположить, что и внутри тела, по плоскостям, параллельным хОу, напряжения пренебрежимо малы, а напряжения , и не зависят от координаты z. Перемещения вдоль оси z происходят, но они представляют собой функцию напряжений и .

Основные уравнения теории упругости, применительно к указанным разновидностям плоской задачи упростятся следующим образом:

1. Плоское деформированное состояние.

Перемещения и = f₁(x, y), v = f₂(x, y) и w = 0.

Деформации из уравнений Коши (1.15)

Напряжение , , и не равны нулю; .

Перейдем к уравнениям закона Гука. По третьей формуле (1.20)

откуда

, (1.25)

т.е. напряжение .

Подставив в формулу (1.20) выражение (1.25), получим

где приведенный модуль упругости

приведенный коэффициент Пуассона

а
б	в

Рис. 16

Аналогично можно преобразовать вторую формулу (1.20).

Приведенный модуль сдвига

(1.26)

Таким образом,

(1.27)

2. Плоское напряженное состояние.

Перемещения u =f₁(x,y); v = f₂(x,y) и w = f₃(x,y).

Деформации = (x, y); = (x, y); = (x, y);

= (x, y); .

Напряжения , и не равны нулю; .

Уравнения закона Гука

(1.28)

3. Уравнения, одинаковые для плоского деформированного и напряженного состояний.

Из трех уравнений равновесия (1.2) ввиду того, что все напряжения не зависят от z, a и равны нулю, остается два:

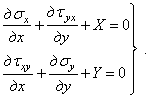(1.29)

Условия на поверхности (1.4) примут вид

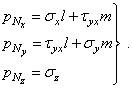(1.30)

Для плоского напряженного состояния p_Nz = 0, так как . Из шести уравнений совместности (1.16) вследствие того, что , и не зависят от z, равно нулю или тоже не зависит от z, а и равны нулю, останется одно

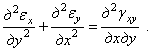(1.31,а)

Если в уравнении (1.31,а) заменить деформации напряжениями, пользуясь формулами (1.28), и получившуюся в правой части уравнения удвоенную производную заменить выражением

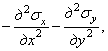
полученным из уравнений (1.29) при условии отсутствия объемных сил, то уравнение совместности деформации может быть представлено в напряжениях

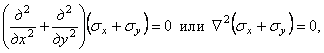(1.31,б)

где – оператор Лапласа.

Путем совместного решения уравнений (1.29) и (1.31,б) могут быть найдены напряжения в случае плоской задачи. Так как в эти уравнения не входят упругие постоянные, можно заключить, что напряженное состояние не зависит от материала.

В случае, если объемные силы имеют потенциал, три составляющих напряжения , и могут быть выражены через одну функцию, называемую функцией напряжений. Если объемная сила имеет только одну проекцию (например, собственный вес), то три составляющих напряжения выражаются через функцию напряжений следующим образом:

Можно убедиться, что эти выражения удовлетворяют уравнениям равновесия (1.29). Подставив в уравнение (1.31,б), получим бигармоническое уравнение плоской задачи

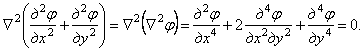
Решение плоской задачи сводится к подысканию функции , удовлетворяющей этому уравнению и условиям на поверхности.

1.11 Плоская задача в полярных координатах

Если тело имеет форму кругового цилиндра или ограничено радиальными и круговыми сечениями цилиндра, плоскую задачу проще решать не в прямоугольных, а в полярных координатах.

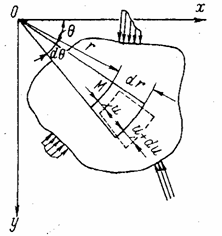
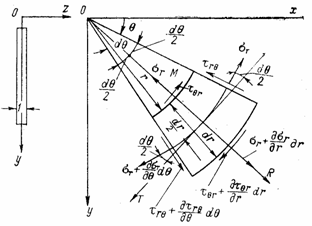
Выделим у точки М тела произвольной формы, имеющего постоянную толщину в направлении оси z, равную единице, и находящегося под действием взаимно уравновешивающихся нагрузок (рис. 17,а), элемент двумя радиальными и двумя окружными сечениями и составим условия его равновесия. На элемент действуют радиальные и окружные нормальные напряжения и касательные напряжения и . Действующие по граням выделенного элемента напряжения, с учетом их приращения вследствие изменения переменных и r, показаны на рис. 17,б.

а		б
в		г

Рис. 17

Составим уравнения равновесия, приравняв нулю суммы проекций всех сил, действующих на элемент, на биссектрису R угла и на касательную Т к окружности радиусом

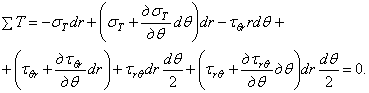
Выполняя перемножение, откидывая величины высшего порядка малости, сокращая подобные члены и деля на , получаем по этим формулам дифференциальные уравнения равновесия в полярных координатах

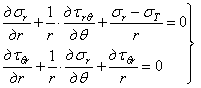. (1.32,а)

Учитывая, что находим, что первые два члена в уравнениях (1.32,а) и (1.29) соответствуют друг другу. Последние члены в каждом из уравнений (1.32,а) выражают особенности полярных координат по сравнению с прямоугольными. Чем ближе элемент к началу координат, тем они больше. Для точки в начале координат при r = 0 уравнения (1.32,а) неприменимы.

Закон Гука для плоского напряженного состояния

. (1.33)

Для плоского деформированного состояния модуль упругости Е, модуль сдвига G и коэффициент Пуассона в формулах (1.33) заменяются приведенными величинами Е', G' и .

Уравнение совместности в полярных координатах при постоянных объемных силах получается из уравнения (1.31,а) путем перехода от декартовых координат к полярным. Координаты r и можно представить в виде функций координат х и у:

.

Поэтому первые частные производные какой-либо функции r и по х и у

.

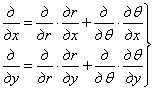Пользуясь выражениями для r и , вычисляем входящие в последние формулы производные и после подстановки этих производных, получаем

.

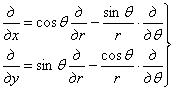Дифференцируя эти выражения, находим вторые производные. Складывая эти производные, получаем для первой скобки уравнения (1.31,а)

.

Для того, чтобы выразить вторую скобку уравнения (1.31,б) в напряжениях и , соответствующих полярным координатам, воспользуемся формулой (1.6). Площадки, по которым действуют нормальные напряжения и , находим, поворачивая оси координат х и у на угол вокруг оси z, как показано на рис. 17,в. Направляющие косинусы для повернутых осей даны в табл. 2.

Таблица 2

Оси	x	y	z
х1	l1 = cos	m1 = sin	n1 = 0
у1	l2 = - sin	m2 = cos	n2 = 0
z1	l3 = 0	m3 =0	n3 = 1

Подставляя в формулу (1.6) соответствующие значения косинусов, получаем для напряжений в полярных координатах (рис. 17,г)

.

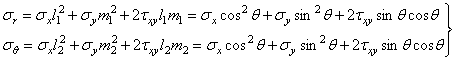Сложение этих формул показывает, что . Тогда уравнение совместности (1.31,б) в полярных координатах принимает вид

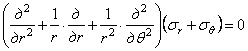. (1.34,а)

Если объемные силы имеют потенциал, все три составляющих напряжения , и в полярных координатах могут быть выражены через одну функцию (r,) напряжений. При отсутствии объемных сил, напряжения выражаются через функцию j следующим образом:

.

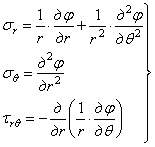При подстановке этих выражений в дифференциальные уравнения (1.32,а) последние превращаются в тождества.

Уравнение совместности (1.34,а), выраженное через функцию напряжений, примет вид

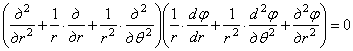. (1.34,б)

В случае осесимметричной плоской задачи при нагрузке, симметричной относительно оси z, касательные напряжения по граням элемента отсутствуют и дифференциальные уравнения равновесия (1.32,а) имеют вид

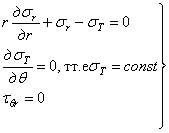. (1.32,б)

Перемещение в случае осесимметричной плоской задачи происходит только в радиальном направлении (и на рис. 17, а) и не зависит от . В окружном направлении в этом случае перемещение отсутствует.

Относительная линейная деформация в радиальном направлении

. (1.35,а)

Относительная линейная деформация в окружном направлении

. (1.35,б)

Относительный сдвиг .

1.12 Возможные решения задач теории упругости

В 15 уравнениях (1.2), (1.15), (1.24) являются неизвестными шесть компонентов напряжений (, , _, , , ), шесть компонентов деформации (, , _, , , ) и три компонента перемещений (и, v, w), т.е. всего 15 неизвестных. Таким образом, с математической точки зрения задача сводится к нахождению 15 функций, удовлетворяющих 15 уравнениям, а также условиям на контуре.

При прямом решении задачи, когда в решении участвуют все 15 уравнений, уравнения неразрывности деформаций, как вытекающие из (1.15) не нужны и могут исполнять роль контрольных уравнений.

Решение указанных трех групп уравнений можно вести разными путями в зависимости от того, что интересует в первую очередь. В связи с этим можно отметить. три направления.

1. Принять за основные неизвестные перемещения точек упругого тела; тогда имеем три неизвестных функции

u = f₁(x,y,z), v = f₂(x,y,z), w =f₃(x,y,z). (1.36)

Для получения решений надлежит в физические уравнения (1.24) подставить геометрические соотношения (1.15), т. е. выразить напряжения через перемещения, и затем полученные выражения подставить в уравнения равновесия, в результате чего получим три уравнения

(u,v,w)=0, (u,v,w)=0, (u,v,w)=0. (1.37)

решение которых приведет к выражениям типа (1.36). Назовем этот метод методом перемещений.

2. Принять за неизвестные напряжения; тогда имеем шесть неизвестных функций

= Ф₁(x,y,z), = Ф₂(x,y,z), = Ф₃(x,y,z),

= Ф₄(x,y,z), = Ф₅(x,y,z), = Ф₆(x,y,z). (1.38)

Так как напряжения из уравнений равновесия непосредственно не определяются, надо обратиться к уравнениям деформаций. Используя, например, уравнения неразрывности деформаций (1.17,а) и (1.17,б) с помощью (1.2) и (1.24) можно получить уравнения в форме:

F₁(,…,) = 0 … F_e(,…,) = 0. (1.39)

дальнейшее решение которых приведет к выражениям типа (1.38). Назовем этот метод методом сил.

3. Очевидно, возможен смешанный, метод, когда за основные неизвестные приняты некоторые из перемещений и некоторые из напряжений.

Что касается способов математического решения полученной системы уравнений, то здесь можно указать несколько направлений.

а) Точное решение прямой задачи, т. е. непосредственное интегрирование уравнений (1.37) или (1.39).

Основные затруднения при решении прямой задачи теории упругости заключаются обычно в точном удовлетворении решения (1.36) или (1.38) граничным условиям. Эти трудности снимаются при решении обратной задачи.

б) Решение обратной задачи, является сравнительно простым (так как связано лишь с дифференцированием функций).

Так, например, задаются перемещениями как функциями координат точки (х, у, z) и разыскивают на основании условий (1.15) деформации, а по ним с помощью (1.24) напряжения; знание последних дает возможность с помощью (1.4) установить поверхностные условия, т. е. внешние нагрузки, которым соответствуют заданные перемещения.

Располагая несколькими решениями обратных задач, каждая из которых соответствует своим граничным условиям, можно комбинированием таких решений получить решение и для некоторых прямых задач.

в) Оказался вполне удобным полуобратный способ Сен-Венана, согласно которому задают часть внешних сил и часть перемещений и разыскивают остальные факторы из условия удовлетворения соответствующих уравнений указанных .выше групп.

Для облегчения решения некоторых уравнений теории упругости оказывается целесообразным способ последовательных приближений.

Одной из разновидностей такого способа оказывается использование в некоторых задачах вначале тех решений, которые являются каким-либо элементарным решением, например, найденным в курсе сопротивления материалов. Подстановка этих решений в уравнения теории упругости приводит к некоторым несоответствиям, из анализа которых можно найти путь корректировки предварительного решения, если и не дающий в итоге точного решения задачи, то приводящий к удовлетворительному для практики приближенному решению (более строгому, чем исходное элементарное решение).

1.13 Решение задач в перемещениях

Из уравнения (1.24) с помощью (1.15) имеем:

(1.40)

где

Дифференцируя (1.40) и внося производные в первое уравнение (1.2), имеем:

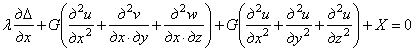. (1.41)

Выражение в первой скобке может быть записано так:

.

Аналогично можно преобразовать и другие два уравнения (1.2), но можно и сразу написать результат, сделав круговую подстановку букв.

Итак, приходим к следующей системе основных уравнений метода перемещений теории упругости:

. (1.42)

Эти уравнения носят название уравнений Ляме. Они являются синтезом статического, геометрического и физического обследований задачи.

Поверхностные условия также можно преобразовать, выразив напряжения через перемещения.

Подставив в первое уравнение (1.4) на место напряжений выражения для них в форме (1.40), имеем:

. (1.43)

Уравнения (1.42) совместно с условиями на поверхности (1.43) позволяют перейти к решению задач теории упругости в перемещениях.

1.14 Решения задач в напряжениях

В противоположность приему, принятому в предыдущем разделе, когда во всех преобразованиях преследовали цель выразить неизвестные через перемещения, можно поставить другую: все выражать через напряжения. Сообщим окончательные результаты и ограничимся случаем статического равновесия тела при условии отсутствия объемных сил или их постоянства.

Трех условий равновесия (1.2) недостаточно, и надо обратиться к условиям неразрывности деформаций (1.17,а) и (1.17,б). Так как в последние входят деформации, их необходимо выразить через напряжения с помощью (1.24). Выполнив эту подстановку и пользуясь одновременно уравнениями равновесия (1.2), уравнения неразрывности преобразуют к следующему виду (уравнения Бельтрами):

, (1.44)

где .

Таким образом, для решения задачи придется проинтегрировать девять уравнений (1.2), (1.44), а входящие в общие решения этих уравнений произвольные функции определить из условий на поверхности (1.4).

1.15 Случай температурного поля

Если элементарный параллелепипед, предположить подверженным только тепловому воздействию, то его деформация характеризовалась бы следующими компонентами:

где а – коэффициент линейного теплового расширения и Т — температура. Будем полагать, что рассматриваемое температурное поле не слишком высокое, чтобы могли измениться упругие характеристики материала (в частности - модуль упругости).

При одновременном наличии компонентов напряжений и теплового эффекта, компоненты деформации, используя (1.20), запишем так:

. (1.45)

Если в первых трех выражениях аТ перевести в левую часть равенств и обозначить

то уравнения (1.45) примут вид, сходный с (1.20) с заменой на , на и на .

В таком случае можно использовать вариант обобщенного закона Гука. Тогда получим:

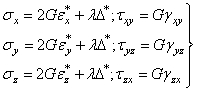. (1.46)

где .

Компоненты уравнений теории упругости для решения такой задачи будут складываться из прежних дифференциальных уравнений равновесия (1.2), прежних геометрических уравнений (1.15), прежних условий на границе (1.4) и новых физических уравнений (1.45) или (1.46), составленных для случая теплового эффекта.

Эти уравнения можно переписать в виде:

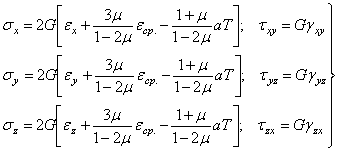. (1.47)

Если теперь проделать выкладки, как в разделе 1.13, то взамен (1.42) придем к уравнениям

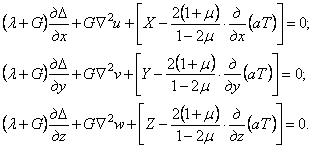(1.48)

Сравнивая (1.48) с (1.47), можно заключить, что при вычислении перемещений неравномерность нагрева тела как бы равносильна добавлению к реальным объемным силам (X, Y, Z) некоторых фиктивных объемных сил, пропорциональных градиентам температур, т. е. пропорциональных а при вычислении напряжений (1.47) появлению дополнительных членов, пропорциональных температуре.

1.15 Краткие выводы

1. Цель математической теории упругости – определить напряжения и деформации при любых нагрузках на границе и внутри упругого тела любой форы.

В отличие от сопротивления материалов, базирующегося на гипотезе плоских сечений и других упрощенных предположениях, теория упругости ставит целью относительно строгое решение задачи при минимальном количестве исходных гипотез.

Задачей точного решения в теории упругости является получение такой системы функций напряжений, смещений и деформаций, чтобы в каждой точке внутри тела были обеспечены условия равновесия и условия непрерывности (сплошности) тела, а у границы тела внутренние силы находились бы в равновесии с внешними силами, действующими на поверхностях (на границе) тела.

2. Для этой цели теория упругости располагает следующими группами уравнений:

а) тремя статическими, уравнениями, справедливыми для каждой точки внутри тела, из которых следует, что интенсивности изменения (градиенты) нормальных и касательных напряжений вдоль координатных осей и сами напряжения между собой не являются независимыми и подчинены определенным дифференциальным соотношениям (1.2).

б) шестью геометрическими уравнениями (1.15), справедливыми для каждой точки внутри тела, из которых, с одной стороны, следует, что компоненты деформации (удлинения и сдвиги) связаны дифференциальными соотношениями с функциями смещений, а с другой стороны (как следствие), интенсивности изменения деформаций вдоль координатных осей и сами деформации между собой не являются независимыми и подчинены определенным дифференциальным соотношениям, именуемым уравнениями неразрывности деформации (1.17,а) и (1.17,б).

в) шестью физическими уравнениями (1.24), справедливыми для каждой точки внутри тела и связывающими компоненты напряжений в каждой точке с компонентами деформации для той же точки.

Иначе говоря, в каждом конкретном теле (со своими упругими характеристиками) указанные непрерывные функции для компонентов напряжений, деформаций и смещений оказываются взаимосвязанными, т. е. существует связь не только между функциями, входящими в каждую отдельную группу, но одной группы уравнений с уравнениями другой группы. Эта взаимосвязь предопределяется физической природой исследуемого тела.

3. В указанные три группы уравнений, составляющие в итоге пятнадцать уравнений, входят пятнадцать неизвестных функций. Принципиально может быть найдено бесчисленное множество решений, каждое из которых обратило бы в тождество все перечисленные уравнения, т. е. обеспечило бы равновесие и непрерывность тела в окрестности любой точки внутри тела. Однако каждое из таких решений соответствовало бы своим особым статическим условиям (внешним нагрузкам) и кинематическим условиям на поверхности тела (наличие или отсутствие тех или иных связей). Поэтому истинным решением задачи будет то, которое увязано с конкретными, заданными граничными условиями и потому конкретное решение должно удовлетворять действительным граничным условиям. Часто эти условия задаются в статическом плане и для каждой точки на границе тела представляются тремя граничными условиями (1.4).

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00