Главная

РАСЧЕТ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК ВРАЩЕНИЯ

Задача 15.1.

Для одной из оболочек, изображенных в таблице 15.2 требуется:

а) Определить начальные параметры M₀, Q₀;

б) Построить эпюры моментов изгибающих, поперечных сил, прогибов, углов поворота по длине оболочки,

в) Определить опасное сечение и вычислить нормальные меридиональные и окружные напряжения.

Толщина цилиндра и сферы постоянна, равна h. Радиус срединных поверхностей – r. Оболочка загружена внутренней распределенной нагрузкой q.

Исходные данные для расчета принять из таблиц 15.1 и 15.2

Таблица 15.1

Номер cтроки	Номер схемы по табл.15.2	l, м	h, м	r, м	q, кН/м^2	E, МПа
01	1	0,25	0,004	0,06	5	210
02	2	0,28	0,005	0,055	4	210
03	3	0,26	0,003	0,075	6	200
04	1	0,24	0,0025	0,08	2	200
05	2	0,22	0,006	0,065	4	210
06	3	0,23	0,0045	0,07	2	200
07	1	0,20	0,003	0,08	3	200
08	2	0,22	0,004	0,085	6	210
09	3	0,26	0,006	0,065	5	210
10	1	0,28	0,009	0,065	6	200
11	2	0,28	0,008	0,08	6	200
12	3	0,22	0,003	0,055	2	210
13	1	0,23	0,003	0,09	4	210
14	2	0,22	0,0025	0,065	2	200
15	3	0,23	0,005	0,085	3	200
16	1	0,24	0,006	0,06	6	210
17	2	0,25	0,006	0,09	5	200
18	3	0,28	0,007	0,075	6	200
19	1	0,30	0,008	0,08	2	210
20	2	0,20	0,008	0,075	4	200
21	3	0,25	0,006	0,065	2	200
22	1	0,25	0,005	0,075	3	210
23	2	0,26	0,006	0,3	6	200
24	3	0,24	0,007	0,25	5	200
25	1	0,25	0,005	0,3	6	210
26	2	0,25	0,005	0,06	6	210
27	3	0,28	0,006	0,055	2	210
28	1	0,26	0,006	0,075	4	200
29	2	0,24	0,007	0,08	2	200
30	3	0,22	0,008	0,065	3	210
31	1	0,23	0,008	0,07	6	200
32	2	0,20	0,006	0,08	5	200
33	3	0,22	0,005	0,085	6	210
34	1	0,26	0,006	0,065	2	210
35	2	0,28	0,007	0,065	4	200
36	3	0,28	0,005	0,08	6	200
	а	в	б	а	г	б

Таблица 15.2. Расчетные схемы оболочек

№ п/п	Схема
1
2
3

Пояснения к решению задачи

Введение

Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми незначительно по сравнению с размерами поверхностей.

1. Линии и радиусы поверхности оболочки

Плоскость, пересекающая поверхность оболочки и проходящая через ось вращения, образует меридиональную линию или меридиан. Линии, перпендикулярные меридианам и оси вращения называют параллелями. Поверхность, равноудаленная от внешней и внутренней поверхностей оболочки, называют срединной и имеющей двояковую кривизну.

Радиус кривизны меридиана – радиус кривизны параллели – . Радиусы и – главные радиусы кривизны поверхности вращения. Важное значение при изучении свойств поверхности имеет гауссова кривизна . На рис. 15.1 даны некоторые формы меридианов при соответствующих К.

При K – меридианы выпуклые (рис. 15.1, а); K – меридианы прямые линии (рис. 1, б); K – меридианы вогнутые (рис. 1, в), при этом, если , то .

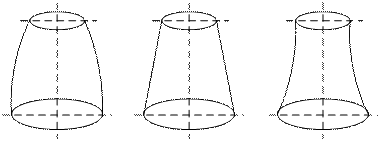
а) б) в)

Рис. 15.1

2. Безмоментная теория осесимметрично нагруженных оболочек

Примером безмоментного состояния служит напряженное состояние, возникающее в оболочке под действием равномерного внутреннего давления. Оболочка испытывает только растяжение. В этом заключается ее преимущество как конструктивного элемента.

В стенках оболочки возникают нормальные меридиональные σ_m и окружные σ_t напряжения (рис. 15.2, а).

Основным признаком безмоментного состояния будет ,

где ε– относительное удлинение срединной поверхности; χ – относительное изменение кривизны; h – толщина стенки. Так напряжение растяжения , а напряжение изгиба – , то, в виду незначительности величины , напряжением σ_u можно пренебречь.

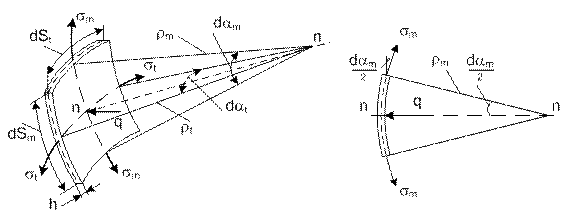
а) б)

Рис. 15.2

Рассмотрим равновесие сил, возникающих от действия внутреннего давления q на элементарной площади и усилий от напряжений меридионального σ_m и тангенциального σ_t с площадями и . На рис. 15.2, б показана меридиональная плоскость. Спроецируем все усилия на общую нормаль n-n:

Заменим синус его аргументом ввиду малости угла и разделим выражение (1) на получим

или, с учетом равенства

окончательно определим

Зависимость (2) называют уравнением Лапласа.

Если принять , то ; и уравнение (2) можно представить как

В уравнение входят два неизвестных напряжения σ_m и σ_t. Определим сначала σ_m, используя уравнение равновесия согласно рис. 15.3.

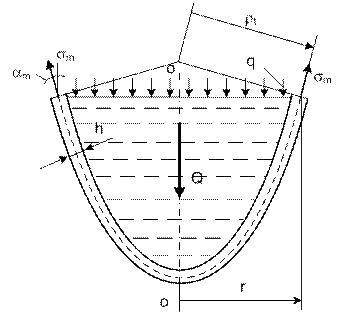
Рис. 15.3

Вырежем часть оболочки вращения, заполненной жидкостью.

Q – веса части жидкости и емкости, лежащие ниже рассматриваемого слоя, q– давление в жидкости с учетом избыточного (по закону Паскаля) ,

где q₀ – избыточное давление в емкости; H – глубина рассматриваемого слоя; γ– объемный вес жидкости. Площадь окружного сечения емкости рассчитаем как: .

Спроецируем силы на ось O - O:

Отсюда:

Подставив (4) в уравнение (2), определим σ_t.

Рассмотрим конкретные расчетные схемы.

3. Сферический сосуд под внутренним давлением q

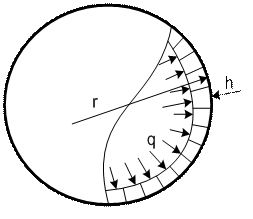
Рис. 15.4

Считаем, что , а (рис. 4), определим

Согласно закона Гука для плоского деформированного состояния, относительная радиальная деформация . В нашем примере

где w – абсолютное приращение радиуса сферы под давлением q.

Считая , с учетом (5) и выражениях относительных деформаций, определим абсолютную деформацию

.

Таким образом,

4. Цилиндрический котел под внутренним давлением

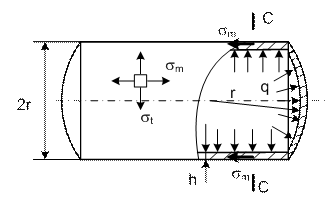
Рис. 15.5

Меридианами считаем образующие котла (см. рис.15.5), т. е. ; , следовательно .

Меридиональное напряжение определим, рассматривая равновесие правой отсеченной части котла по сечению C-C.

Следовательно, окружное напряжение в два раза больше меридионального. Используя выкладки предыдущего примера, выразим абсолютное радиальное перемещение

Отсюда,

5. Подвешенная цилиндрическая оболочка с коническим днищем

Наполнена жидкостью объемным весом γ, (см. рис. 15.6).

Определить напряжения σ_t , σ_m в цилиндрической и конической частях, построить эпюры напряжений.

Начало вертикальной координаты x в днище оболочки; r_y – текущий радиус конической части; 2α – угол конуса днища.

Рассмотрим коническую часть.

Давление жидкости на глубине H+H₁-x равно .

Т. к. ; . Проекция ρ_t на горизонтальную ось . Выразим r_y через радиус оболочки . Окружное напряжение конической части примет вид:

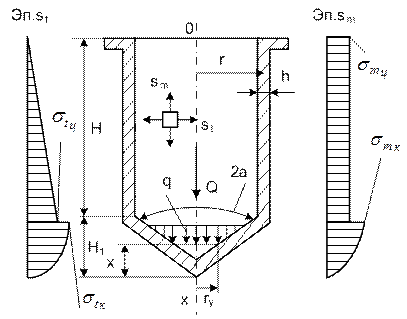
Рис. 15.6

При x=H₁; ;

при x=-(H+H₁); (см. эп., рис. 15.6).

Цилиндрическая часть.

Воспользуемся уравнением (4):

Выразим q через объемный вес, r_y – через радиус оболочки.

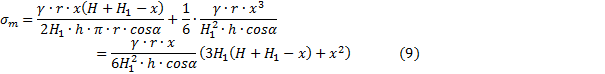
Вес жидкости в конической части высотой x равен объему конуса на объемный вес жидкости

При x=H₁; ;

при x=H₁; и α=0; .

Эпюры σ_m даны на рис. 15.6. Разрывы на эпюрах вызваны краевыми эффектами.

6. Краевой эффект в цилиндрической оболочке (моментная теория расчета оболочек)

Длинные цилиндрические оболочки соединены фланцами, являющимися более жесткими по отношению к оболочкам. Оболочка, находящаяся под внутренним давлением q может увеличить начальный диаметр. Вследствие этого на некотором участке от фланца стенки оболочки получают искривление. Исследуем напряженное состояние и изгиб стенок оболочки (краевой эффект), считая, что продольные усилия в поперечном сечении отсутствуют.

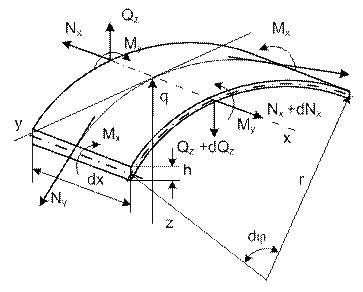
Рис. 15.7

В общем случае изгиб цилиндрической оболочки включает десять уравнений равновесия элемента. Из них поперечная сила Q_y=0; моменты крутящие ; сдвигающие силы .

Погонные моменты M_x и поперечные силы N_y, в виду симметрии относительно оси X не получают приращения в радиальных сечениях. Остальные уравнения равновесия, согласно рис. 15.7, при h=1:

отсюда

Заменим , сократив на dφ∙dx, получим

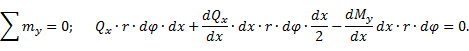
Второе слагаемое, в виду малости, отбрасываем, получим . Подставим данное выражение в (10), имеем

В выражении (10) два неизвестных. Введем дополнительное уравнение погонных продольных сил

В дальнейшем, от дифференциальных уравнений в усилиях перейдем к дифференциальным уравнениям в радиальных перемещениях. Для этого выразим усилия через деформации, а деформации – через перемещения.

Закон Гука при плоском напряженном состоянии (σ_z=0):

Усилия при ширине вырезанного участка, равного единице, примут вид

Приравняем N_x выражений (12) и (14), получим

Относительная радиальная деформация, при условии сохранения формы окружности,

Погонная поперечная сила N_y, с учетом (15) и (16), равна

Дополнительный погонный изгибающий момент от силы N_x имеет значение

Изгибающие моменты от внутреннего давления q, соответственно равны,

При равномерном радиальном расширении цилиндрической оболочки приращение перемещения к приращению радиуса остается постоянным, поэтому моменты примут вид

Полный момент

Подставим (17) в (11), имеем раскрывая полученное выражение, учетом (12) и (17), окончательно определяем или

Выражение (21) – дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях.

Влияние продольной силы N_x на изменение w незначительно и ею можно пренебречь. Тогда (равенство нулю N_x) приближенное уравнение равновесия примет вид Данное выражение можно записать как

Уравнение (22) можно преобразовать, обозначив

где – коэффициент затухания перемещений, 1/м.

При q=0 уравнение (23) примет вид (24)

балки на упругом основании.

Четырежды интегрируя уравнение (23), получим перемещение срединной поверхности оболочки

где f(x) – частное решение; при q=const по всей длине оболочки, .

Следовательно, все силы и моменты можно определить как

Угол наклона касательной к срединной поверхности

7. Расчет длинной цилиндрической оболочки (защемление с двух сторон)

Признаком длинной оболочки считают выражение .

В уравнении (25) при ; , что противоречит условию закрепления второго торца, следовательно, C₁ и C₂ равны нулю.

Уравнение (25) примет вид

. (26)

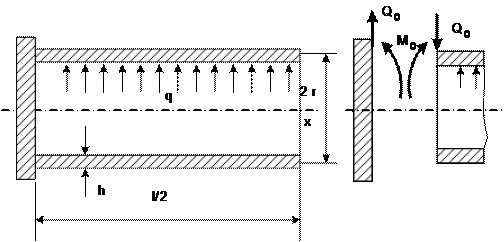
а) б)

Рис. 15.9

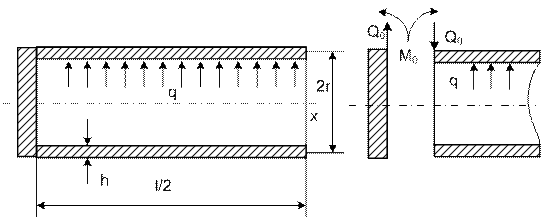
На рис. 15.9 показана половина оболочки с защемлением левого торца, загруженная внутренним давлением q.

Расчетную схему представим как цилиндрическую оболочку, загруженную по левому торцу моментом и силой. Это возможно, если отделить массивный фланец от цилиндрической оболочки (рис.15.9 б).

Для определения C₃ и C₄ продифференцируем уравнение (26):

При x=0;

где Q₀ и M₀ – поперечная сила и момент в защемлении.

Приравняем выражения (26б) и (26в), соответственно M₀ и Q₀, получим

Частное решение уравнения (26) получим согласно граничным условиям данной схемы: равенства нулю прогиба и угла поворота срединной поверхности оболочки ; .

По уравнению (26) имеем ; по уравнению (26а) – C₃=C₄. В уравнении (27) заменим . После преобразования, получим , учитывая, что .

Произведя замену и, с учетом уже известного выражения , получим значение .

Используя зависимости внутренних силовых факторов от производных w, определим и построим их эпюры.

Согласно условию прочности, определим окружное и тангенциальное напряжения и , сравним с допускаемыми. В случае невыполнения, произведем коррекцию толщины оболочки.

8. Расчет цилиндрической оболочки, шарнирно опертой по концам

Расчетная схема представлена рис. 15.10.

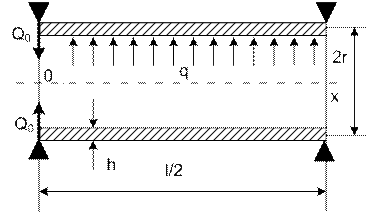
Рис.15.10

Уравнение прогиба цилиндрической оболочки, согласно (26),

.

Граничные условия: x=0; ;

Определение значения Q₀.

Уравнение (26) преобразуем к виду:

Частное решение уравнения (26) получим согласно граничным условиям данной схемы: равенства нулю прогиба срединной поверхности оболочки :

Уравнения углов поворота срединной поверхности, погонного момента меридионального и погонной поперечной силы, соответственно, примут выражения:

Напряжения, меридиональные и окружные, определяют по известным зависимостям

В дальнейшем, строят эпюры, определяют опасные сечения и, в случае несоблюдения условий прочности (жесткости) проводят коррекцию толщины оболочки.

9. Примеры расчета оболочек вращения

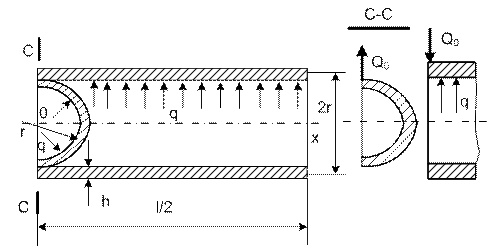
9.1. Цилиндрическая оболочка со сферическим днищем

На рис. 15.11 изображена цилиндрическая оболочка вращения со сферическим днищем. Толщина цилиндра и сферы постоянна, равна h. Радиус срединных поверхностей – r. Оболочка загружена внутренней распределенной нагрузкой q.

Определить:

а) Начальные параметры M₀, Q₀;

б) Построить эпюры моментов изгибающих, поперечных сил, прогибов, углов поворота по длине оболочки,

в) Определить опасное сечение и вычислить нормальные меридиональные и окружные напряжения.

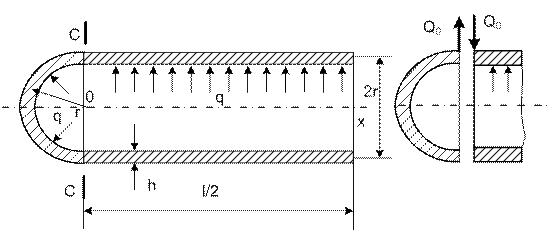
Рис. 15.11

1. Определяем цилиндрическую жесткость оболочки

2. Вычисляем коэффициент затухания перемещений

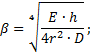
3. Выбираем начало координат в сечении C-C – переходе из цилиндрической оболочки в сферическую;

4. Рассматриваем взаимное равновесие полусферической и цилиндрической оболочек. Читаем, что общая касательная в переходе от цилиндрической оболочки к сферической поворачивается под действием Q₀ на одинаковый угол. Взаимный угол поворота отсутствует, следовательно, не возникает взаимный погонный изгибающий момент M₀.

Суммарные взаимные линейные деформации от действия Q₀ и q равны:

где – радиальное перемещение цилиндрической оболочки от действия q; – максимальное перемещение сферического днища от действия q; .

Так как и, согласно (27),

Отсюда . С учетом , определяют .

5. Уравнение прогибов ;

6. Уравнение углов поворота срединной поверхности

7. Уравнение погонного момента радиального

8. Уравнение погонной радиальной силы

9.2. Цилиндрическая оболочка с плоским днищем

Оболочка нагружена внутренним давлением q. Толщина цилиндра и днища равны h (рис.15.12).

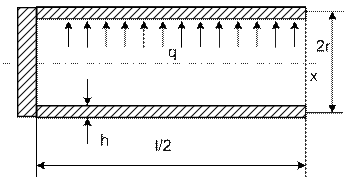
Рис. 15.12

Рассмотрим половину длины оболочки. Разделив днище и цилиндр, представим днище в виде круглой пластины, защемленной по контуру, рис. 15.13 а.

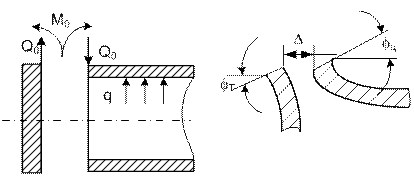
а) б)

Рис.15.13

Уравнение углов поворота срединной плоскости пластины . Граничные условия: при r=0 (середина днища) φ=0; следовательно, C₂=0. При этом – цилиндрическая жесткость днища.

Радиальный погонный момент . Из теории круглых пластин Радиальный момент на контуре соответствует .

Отсюда, Следовательно, .

Окончательно, уравнение угла поворота срединной поверхности днища примет вид:

Радиальный погонный изгибающий момент

где r₀ – текущий радиус пластины (днища).

Считают, что радиальные перемещения пластины малы, , взаимное радиальное перемещение пластины и оболочки . С учетом (27) радиальное перемещение оболочки

Остается сравнить взаимные угловые перемещения днища и цилиндрической оболочки

Совместное решение (а) и (б) дает

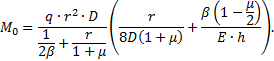
1. Уравнение прогибов цилиндрической оболочки

2. Угол поворота срединной поверхности

3. Погонный изгибающий радиальный момент

4. Погонная поперечная сила

5. Радиальное напряжение сравнить с допускаемым и, в случае необходимости, откорректировать h.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00