Главная

Задача 1. Расчет тонкостенных стержней открытого профиля при стесненном кручении

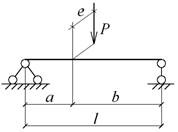
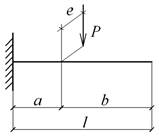
Для заданного типа поперечного сечения балки:

- определить положение центра тяжести;

- построить эпюры линейных координат;

- вычислить осевые моменты инерции сечения;

- построить эпюру секториальных координат;

- определить положение центра изгиба;

- построить эпюру главных секториальных координат;

- вычислить главный секториальный момент инерции сечения;

- вычислить момент инерции сечения при чистом кручении;

- вычислить изгибно-крутильную характеристику сечения.

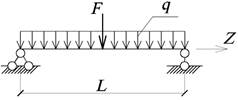
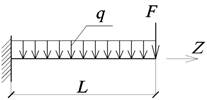
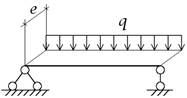
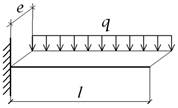
Для заданной расчетной схемы балки:

- записать аналитические выражения для определения внутренних усилий;

- рассчитать значения внутренних усилий для характерных сечений (опорные сечения, середина и четверти пролета);

- построить эпюры внутренних усилий (Q_x или Q_y, M_x или M_y, B_ω, M_ω, M₀, M_z).

Для опасных сечений балки:

- определить величину нормальных и касательных напряжений;

- построить эпюры нормальных и касательных напряжений (от воздействия каждого внутреннего усилия и результирующие).

Исходные данные для выполнения курсовой работы приведены в табл. 1-4.

В табл. 1 даны геометрические характеристики поперечного сечения балки, а также тип сечения.

В табл. 2 даны нагрузки, действующие на балку, а также длина и тип закрепления балки.

В табл. 3 даны типы поперечных сечений балки, а также расположение нагрузки. Тип поперечного сечения выбирается в соответствии с табл. 1.

В табл. 4 даны типы закреплений балки, а также расположение нагрузки. Тип закрепления балки выбирается в соответствии с табл. 2.

Таблица 1. Геометрические характеристики сечения

Номер строки	Тип сечения (по табл.1)	B, см	H, см	δ, см
1	A	24	30	1,4
2	B	32	40	1,6
3	A	40	44	1,8
4	B	28	36	2,0
5	C	24	30	1,4
6	D	24	30	1,6
7	C	32	40	1,8
8	D	32	40	2,0
9	A	32	40	1,4
10	C	40	44	1,6
11	A	46	44	1,8
12	C	28	36	2,0
13	B	24	30	1,4
14	D	40	44	1,6
15	B	40	44	1,8
16	D	28	36	2,0
17	A	28	36	1,4
18	B	24	36	1,6
19	C	46	40	1,8
20	D	46	40	2,0
21	D	30	40	1,4
22	C	28	40	1,6
23	B	30	40	1,8
24	A	30	40	2,0
25	C	30	40	1,4
	в	г	б	а

Таблица 2. Нагрузки, действующие на балку

Номер строки	F1, кН	F2, кН	q1, кН/м	q2, кН/м	L, м	Тип закрепления балки (по табл.4)
1	18	-	-	-	6	I
2	-	-	8	-	7	II
3	30	-	-	-	8	I
4	-	-	-	10	5	II
5	-	26	-	-	4	I
6	-	-	12	-	4	II
7	-	28	-	-	5	I
8	28	-	-	-	6	II
9	-	-	15	-	7	I
10	26	-	-	-	8	II
11	-	-	15	-	8	I
12	-	-	-	12	7	II
13	-	18	-	-	6	I
14	-	30	-	-	5	II
15	-	-	10	-	4	I
16	-	-	-	15	4	II
17	-	-	-	8	5	I
18	18	-	-	-	6	II
19	30	-	-	-	7	I
20	-	28	-	-	8	II
21	-	26	-	-	8	I
22	-	-	10	-	7	II
23	-	-	12	-	6	I
24	-	-	-	8	5	II
25	-	-	-	15	4	I
	в	г	а	б	г	в

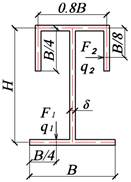
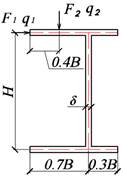
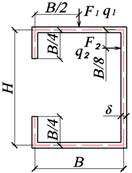
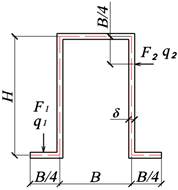
Таблица 3. Типы поперечных сечений балки

Тип поперечного сечения балки
A	B	C	D

Таблица 4. Типы закреплений балки

Тип закрепления балки
I	II

Методические указания

1. Теоретические сведения о тонкостенном стержне

Тонкостенным стержнем называется такой стержень, у которого один из линейных размеров поперечного сечения мал по сравнению с остальными.

Тонкостенные стержни могут быть закрытого профиля (трубчатое, коробчатое сечения) и открытого профиля (тавр, двутавр, швеллер и т.п.).

В стержнях открытого профиля наиболее отчетливо проявляются особенности их расчета.

Тонкостенные стержни как расчетная схема сохраняют в себе основные свойства бруса при работе на растяжение, сжатие, изгиб и кручение. Вместе с тем тонкостенный стержень в силу своих геометрических особенностей проявляет свойства, существенно отличающие его от стержней сплошного сечения:

- не всегда применим принцип Сен-Венсана с равномерным распределением усилий в сечении стержня;

- не соблюдается закон плоских сечений, происходит депланация за счет продольных перемещений точек поперечного сечения.

Условия крепления стержня влияют на депланацию поперечного сечения. Если депланация в различных поперечных сечениях различна, деформация называется стесненным кручением (рис.1).

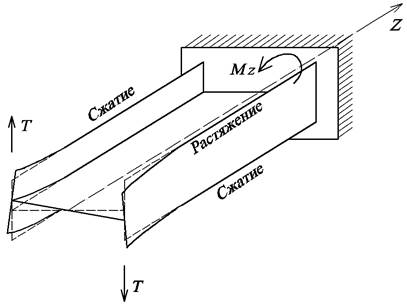
Рис.1. Стесненное кручение стержня

Депланация приводит к возникновению не только касательных, но и нормальных напряжений в поперечных сечениях стержня. Таким образом, при стесненном кручении тонкостенных стержней открытого профиля одновременно имеют место деформации кручения и изгиба.

Внутренние усилия в поперечных сечениях при стесненном кручении приводятся:

- к самоуравновешенной системе двух пар равных продольных сил N (рис. 2), которые называются бимоментом B_ω;

-к изгибающему моменту M_x или M_y;

-к поперечной силе Q_y или Q_x;

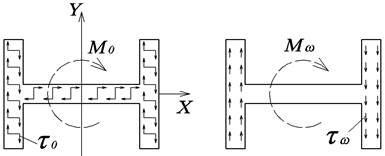
-к моменту чистого кручения M_o (рис. 3, а);

-к изгибно-крутящему моменту M_ω (рис. 3, б).

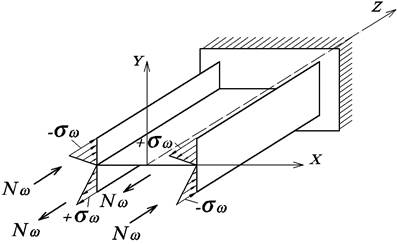
Рис.2. Образование бимомента

а б

Рис. 3. Внутренние усилия:

а – момент чистого кручения; б – момент изгибно- крутящий

2. Порядок выполнения задания

2.1. Определение положения центра тяжести, величины главных центральных моментов инерции поперечного сечения

Координаты центра тяжести поперечного сечения относительно произвольных осей X₁ и Y₁ определяются по формулам

где А – площадь поперечного сечения; S_y1– статический момент площади относительно оси Y₁; S_x1– статический момент площади относительно оси X₁.

Для определения главных центральных моментов инерции поперечного сечения J_x и J_y необходимо выполнить построение эпюр линейных координат X и Y в главных центральных осях сечения.

Вычисление J_x и J_y для тонкостенных стержней выполняется перемножением эпюр линейных координат с учетом толщины элементов поперечного сечения по правилу Верещагина:

2.2. Определение координат центра изгиба

Центром изгиба называется такая точка, через которую должна проходить плоскость действия внешних сил, чтобы балка испытывала только деформацию изгиба (не подвергалась кручению).

Координаты центра изгиба А определяются по формулам

где S_ωBy– секториально-линейный статический момент сечения относительно оси Y; S_ωBx– секториально-линейный статический момент сечения относительно оси X.

S_ωBx и S_ωBy вычисляются перемножением эпюр линейных координат с эпюрой секториальных координат ω_B по правилу Верещагина с учетом толщины элементов поперечного сечения:

Секториальная координата определяется по формуле

Секториальная координата ω_B представляет собой удвоенную площадь сектора M₀BM₁, образованную поворотом радиуса-вектора r относительно полюса B от начального положения BM₀ до BM₁ (рис.4) .

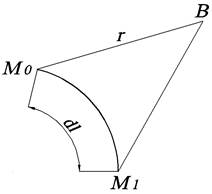
Рис. 4. Нахождение секториальной координаты

Если поворот радиуса-вектора r вокруг полюса В от точки начала отсчета M₀ к точке M₁ осуществляется против хода часовой стрелки, то секториальная координата положительна. Для определения положения центра изгиба выполняется построение эпюры секториальных координат ω_B. Полюс В и точку начала отсчета M₀ располагают на контуре сечения по оси симметрии. Координаты центра изгиба откладываются от полюса В.

2.3. Построение эпюры главных секториальных координат поперечного сечения

Для построения эпюры главных секториальных координат ω₀ полюс располагают в центре изгиба А, точку отсчета M₀ – на контуре сечения по оси симметрии.

Обязательной проверкой правильности вычисления координат центра изгиба является равенство нулю секториально-линейного статического момента S_ω0x или S_ω0y, который вычисляется перемножением эпюры главных секториальных координат ω₀ с соответствующей эпюрой линейных координат:

Погрешность вычислений не должна превышать 1%.

2.4. Вычисление момента инерции при чистом кручении J_K, секториального момента инерции J_ω0, изгибно-крутильной характеристики K

Момент инерции чистого кручения определяется по формуле

где α– коэффициент, зависящий от формы сечения; b_i – наибольший размер элемента сечения; δ_i – толщина элемента сечения.

Для двутаврового сечения α=1,20; для швеллера α=1,12; для таврового сечения α=1,15.

Секториальный момент инерции вычисляется перемножением эпюры ω₀ с учетом толщины по правилу Верещагина:

Изгибно-крутильная характеристика

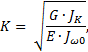
где модуль упругости I рода E=200 ГПа; модуль упругости II рода G=80 ГПа.

2.5. Определение начальных параметров внутренних усилий и деформаций при стесненном кручении тонкостенных стержней открытого профиля

Величина внутреннего усилия в сечении тонкостенного стержня определяется методом начальных параметров по табл. 5, где θ₀ – угол закручивания в начале координат; θ₀^/ – относительный угол закручивания в начале координат; B_ω0 – бимомент в начале координат; M_K0 – крутящий момент в начале координат. Начало координат располагается в левом сечении стержня.

Из четырех начальных параметров два неизвестных. Неизвестные начальные параметры определяются из условия крепления балки справа. Таким образом, при любом креплении однопролетной балки необходимо решать не более двух уравнений, вытекающих из условия опирания правого сечения балки (табл. 5).

Таблица 5

№ схемы	Схема закрепления балки	Начальные параметры
1
2
3
4

2.6. Построение эпюр внутренних усилий

Аналитические выражения для определения внутренних усилий и деформаций можно составить по табл. 5.

По результатам вычислений выполняется построение эпюр внутренних усилий: Q_X или Q_Y – поперечных сил; M_y или M_x– изгибающих моментов; B_ωx– бимомента; M₀– момента чистого кручения; M_ω – изгибно-крутящего момента; M_K – внешнего крутящего момента.

2.7. Вычисление нормальных напряжений

В сечениях тонкостенных стержней открытого профиля при стесненном кручении возникают нормальные напряжения

где N – продольная сила в сечении;M_y– изгибающий момент относительно оси Y; M_x– изгибающий момент относительно оси X; B_ω– изгибно-крутящий бимомент; А – площадь поперечного сечения;

J_x– момент инерции относительно оси Х; J_y – момент инерции относительно оси Y; J_ω0 – секториальный момент инерции;

Х, Y – эпюры линейных координат; ω₀– эпюра главных секториальных координат.

2.8. Вычисление касательных напряжений

Касательные напряжения при стесненном кручении тонкостенных стержней определяются выражением

где Q_X– поперечная сила по направлению оси X; Q_Y– поперечная сила по направлению оси Y; M₀– момент при чистом кручении; M_ω– изгибно-крутящий момент; J_K– момент инерции сечения при чистом кручении; J_ω– секториальный момент инерции; – эпюра статического момента отсеченной части сечения относительно оси Х; – эпюра статического момента отсеченной части сечения относительно оси Y; –– площадь отсеченной части эпюры главных секториальных координат.

Для пояснения теории расчета тонкостенных стержней далее приведено несколько примеров.

3. Примеры выполнения задания

3.1. Пример №1

3.1.1. Исходные данные

Таблица 6. Исходные данные

В, см	30
Н, см	40
δ, см	2
q, кН/м	15
L, м	4
Е, ГПа	200
G, ГПа	80

В табл. 6 приведены исходные данные для примера №1. На рис. 5 и 6 даны поперечное сечение и расчетная схема рассматриваемого стержня.

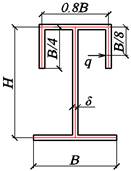
Рис. 5. Поперечное сечение

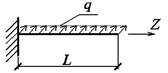
Рис. 6. Расчетная схема

3.1.2. Определение положения центра тяжести, величины главных центральных моментов инерции поперечного сечения

Площадь поперечного сечения

Статический момент площади относительно оси X₁

Координаты центра тяжести (рис. 7)

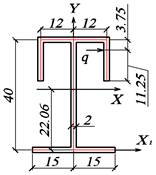
Рис. 7. Координаты центра тяжести

Моменты инерции относительно центральных осей (вычисляются при помощи эпюр линейных координат рис. 8 и 9)

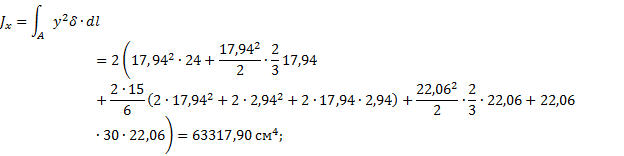
=15444

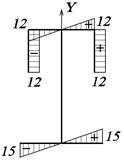
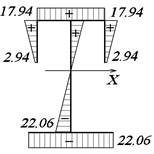
Рис.8. Эпюра Х, см Рис.9. Эпюра Y, см

3.1.3. Определение координат центра изгиба

Для определения центра изгиба строим эпюру секториальных координат (рис. 10) с произвольным полюсом В и началом отсчета M₀. B и M₀ располагаем на контуре по оси симметрии сечения.

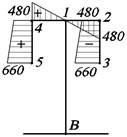
Рис.10. Эпюра ω_В, см²

Секториальную координату определяем по формуле

Секториально-линейный статический момент относительно оси Y вычисляем перемножением эпюр ω_B и X по формуле

Определяем координаты центра изгиба

a_y откладываем от полюса B по оси Y, получаем центр изгиба А (рис. 11).

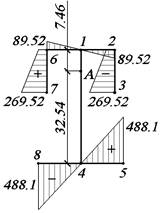
Рис.11. Эпюра ω₀, см²

3.1.4. Построение эпюры главных секториальных координат поперечного сечения

Проверка правильности определения положения центра изгиба:

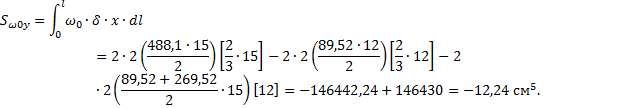
Эпюра ω₀ построена правильно, положение центра изгиба верное.

3.1.5. Вычисление момента инерции при чистом кручении J_K, секториального момента инерции J_ω0, изгибно-крутильной характеристики K

Для двутаврового сечения α=1,2.

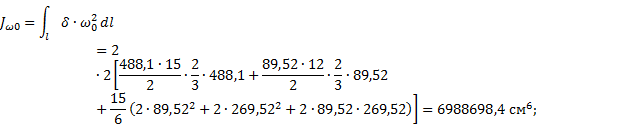
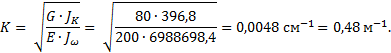
3.1.6. Определение неизвестных начальных параметров

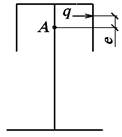
Рис.12. Нахождение эксцентриситета

На рис.12 показан эксцентриситет е.

Z=0; z=L;

θ₀=0; B_ωL=0;

θ₀^/=0; M_KL=0.

где

При z=L по табл. 5

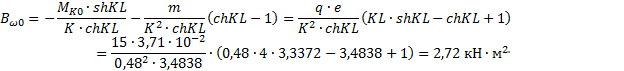
3.1.7. Определение ординат для построения эпюры бимоментов B_ω

По табл. 5

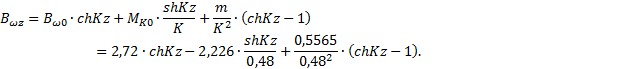
С шагом в 1 м длины балки определяем

B_ω0=2,72 кН·м²;

3.1.8. Определение ординат для построения эпюры изгибно-крутящих моментов M_ω

По табл. 5

M_ω0=-2,226 кН·м;

3.1.9. Определение ординат для построения эпюры моментов чистого кручения M_0z

По табл.5

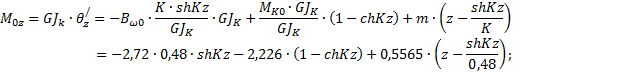
M_O0=0;

3.1.10. Определение ординат для построения эпюры внешних крутящих моментов M_Kz

Результаты вычислений внутренних усилий сводим в табл.7.

Таблица 7. Внутренние усилия

z	Kz					shKz	chKz
0	0	-2,226	0	2,72	-2,226	0	1
1	0,48	-1,6695	-0,411	1,011	-1,258	0,4986	1,1174
2	0,96	-1,113	-0,527	0,106	-0,586	1,1144	1,4973
3	1,44	-0,5565	-0,505	-0,207	-0,051	1,9919	2,2288
4	1,92	0	-0,471	0	0,471	3,3372	3,4838

3.1.11. Построение эпюр внутренних усилий (рис.13)

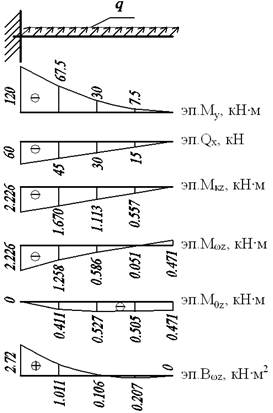
Рис. 13. Эпюры внутренних усилий

3.1.12. Построение эпюры нормальных напряжений в опасном сечении стержня

Нормальные напряжения

По эпюрам M_y и B_ω опасным сечением в консольной балке является опорное.

M_y=120 кН∙м=-120∙10^-3 МН∙м;

В_ω=2,72 кН∙м²=2,72∙10^-3 МН∙м²;

Эпюры σ_u и σ_ω построены с помощью эпюр X и ω₀. Эпюру σполучаем суммированием эпюр σ_u и σ_ω (рис. 14, в).

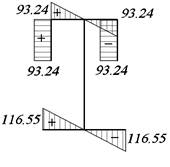
а б в

Рис. 14. Эпюры нормальных напряжений:

а – эпюра 𝜎_u, МПа; б – эпюра σ_ω, МПа; в – эпюра σ, МПа

3.1.13. Построение эпюр касательных напряжений в опасном сечении стержня

Касательные напряжения

По эпюрам опасным является опорное сечение.

Касательные напряжения от изгиба

где – статический момент отсеченной части сечения относительно оси Y. считается с помощью рис. 15.

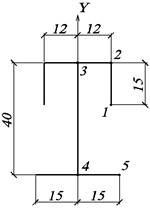
Рис. 15. Расчетные точки

Остальные участки симметричны найденным.

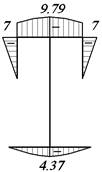
Рис. 16. Эпюра τ_u, МПа

Касательные напряжения от изгиба (рис. 16)

Определяем напряжения от изгибно-крутящего момента.

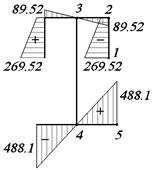
Рис. 17. Эпюра ω₀, см²

Эпюра (рис. 18) строится с помощью эпюры ω₀ (рис. 17).

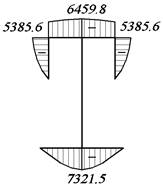
Рис. 18. Эпюра S_ω^отс, см³

Касательные напряжения от изгибно-крутящего момента (рис. 19)

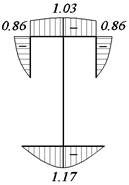
Рис. 19. Эпюра τ_ω, МПа

Находим напряжения от чистого кручения в опорном сечении так как в опорном сечении M₀=0.

Эпюру τ получаем суммированием эпюр τ_u, τ_ω и τ_o (рис.20).

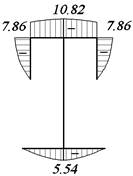
Рис. 20. Эпюра τ, МПа

3.1.14. Нахождение угла закручивания

При z=L

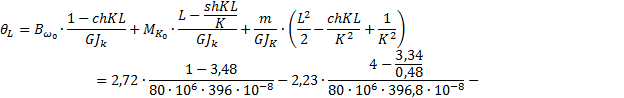
3.2. Пример №2

3.2.1. Исходные данные

В табл. 8 приведены исходные данные для примера №2. На рис. 21 и 22 даны поперечное сечение и расчетная схема рассматриваемого стержня.

Таблица 8. Исходные данные

В, см	40
Н, см	44
𝛿, см	1,6
q, кН/м	15
L, м	8
Е, ГПа	200
G, ГПа	80

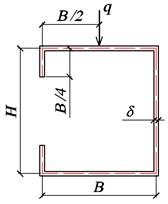
Рис. 21. Поперечное сечение

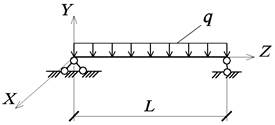
Рис. 22. Расчетная схема

3.2.2. Определение положения центра тяжести, величины главных центральных моментов инерции поперечного сечения

Площадь поперечного сечения

Статический момент площади относительно оси Y₁

Координата центра тяжести (рис.23)

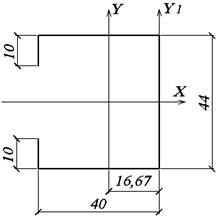
Рис. 23. Координаты центра тяжести

Для тонкостенных стержней моменты инерции J_x и J_y вычисляем перемножением эпюр линейных координат по правилу Верещагина (при помощи эпюр линейных координат рис. 24 и 25):

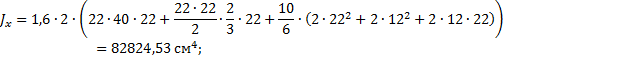
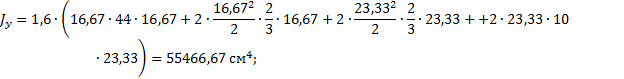
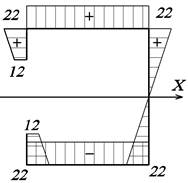
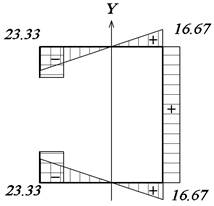
Рис. 24. Эпюра Y, см Рис. 25. Эпюра X, см

3.2.3. Определение координат центра изгиба

Для определения центра изгиба строим эпюру секториальных координат с произвольным полюсом В (рис. 26).

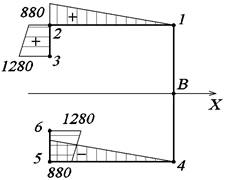
Рис. 26. Эпюра ω_В, см²

Секториальную координату определяем по формуле

Секториально-линейный статический момент относительно оси Х вычисляем перемножением эпюр ω_B и Y по формуле

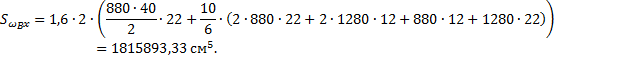
Определяем координаты центра изгиба

a_x откладываем от полюса В по оси Х, получаем центр изгиба А (рис. 27).

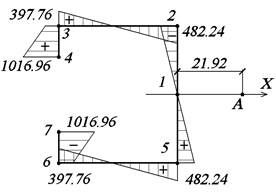
Рис. 27. Эпюра ω₀, см²

3.2.4. Построение эпюры главных секториальных координат поперечного сечения

Эпюру главных секториальных координат строим, располагая полюс в центре изгиба А (рис.27).

Проверка правильности определения положения центра изгиба:

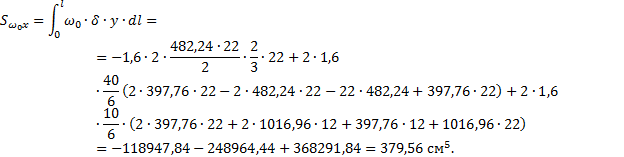
Эпюра ω₀ построена правильно, положение центра изгиба верное.

3.2.5. Вычисление момента инерции при чистом кручении J_K, секториального момента инерции J_ω0, изгибно-крутильной характеристики K

Для данного сечения α=1,12.

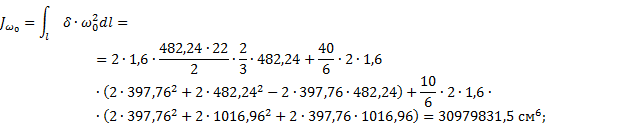
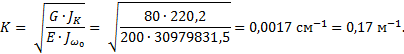
3.2.6. Определение неизвестных начальных параметров

На рис.28 показан эксцентриситет е

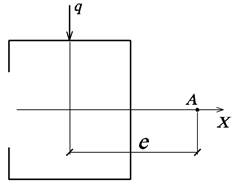
Рис. 28. Нахождение эксцентриситета

e=21,92+20=41,92 см;

m=q∙e=15∙41,92∙10^-2 =6,288 кНм/м.

Начальные параметры для способа закрепления, показанного на рис. 29.

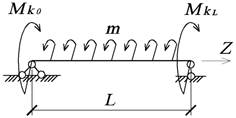
Рис. 29. Расчетная схема

z=0; z=L;

θ₀=0; θ_L=0;

При z=L по табл. 5

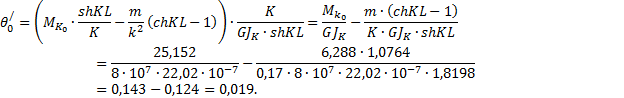
3.2.7. Определение ординат для построения эпюры бимоментов B_ω

По табл. 5

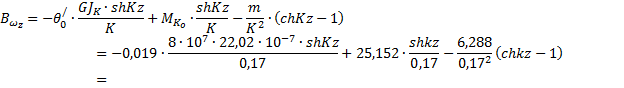
Ввиду симметрии нагрузки эпюра симметрична, поэтому для ее построения достаточно определить ординаты для половины балки.

3.2.8. Определение ординат для построения эпюры изгибно-крутящих моментов M_ω

По табл.5

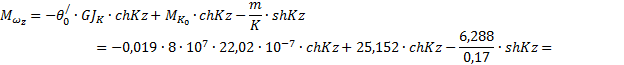
Для определения ординат эпюры составляем уравнения для половины балки, так как при симметричной нагрузке эпюра кососимметрична.

3.2.9. Определение ординат для построения эпюры моментов чистого кручения

По табл.5

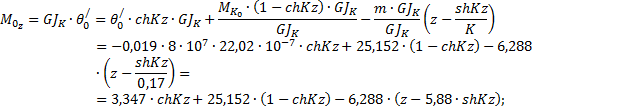
3.2.10. Определение ординат для построения эпюры внешних крутящих моментов

Результаты вычислений внутренних усилий сводим в табл.9.

Таблица 9. Внутренние усилия

z	Kz	shKz	chKz
0	0	0	1	0	25,152	3,347	21,805
1	0,17	0,171	1,014	18,759	18,864	3,060	15,804
2	0,34	0,347	1,058	31,758	12,576	2,315	10,261
3	0,51	0,532	1,133	39,373	6,288	1,274	5,014
4	0,68	0,734	1,240	41,827	0	0	0
5	0,85	0,956	1,384	-39,373	-6,288	-1,274	-5,014
6	1,02	1,206	1,567	-31,758	-12,576	-2,315	-10,261
7	1,19	1,491	1,796	-18,759	-18,864	-3,060	-15,804
8	1,36	1,820	2,076	0	-25,152	-3,347	-21,805

Проверка:

3.2.11. Построение эпюр внутренних усилий (рис.30)

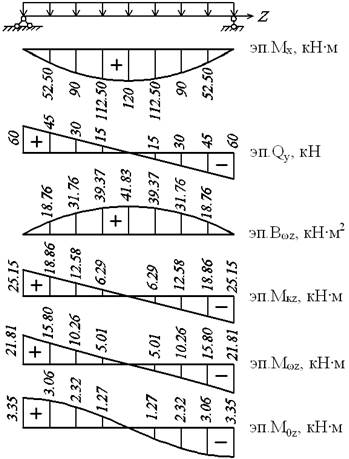
Рис.30. Эпюры внутренних усилий

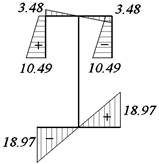
3.2.12. Построение эпюры нормальных напряжений в опасном сечении стержня

Нормальные напряжения

По эпюрам M_x и B_ω опасным сечением является середина стержня.

Эпюры σ_u и σ_ω построены с помощью эпюр Y и ω₀. Эпюру σ получаем суммированием эпюр σ_u и σ_ω (рис. 31, в).

Наибольшие нормальные напряжения

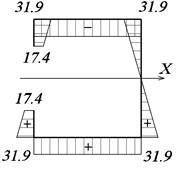
а б в

Рис.31. Эпюры нормальных напряжений:

а – эпюра σ_u, МПа; б – эпюра σ_ω, МПа; в – эпюра σ, МПа

3.2.13. Построение эпюр касательных напряжений в опасном сечении стержня

Касательные напряжения

По эпюрам опасным является опорное сечение.

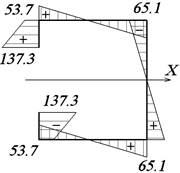
Находим касательные напряжения от изгиба (рис. 33).

где - статический момент отсеченной части сечения относительно оси Х. считается с помощью рис. 32.

Остальные ординаты симметричны найденным.

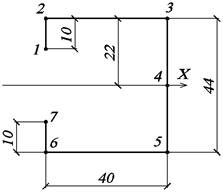
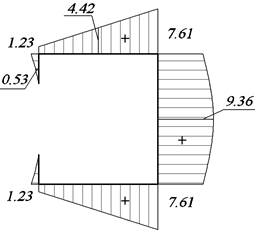
Рис. 32. Расчетные точки Рис. 33. Эпюра τ_u, МПа

Находим напряжения от изгибно-крутящего момента (рис. 36).

Эпюра (рис. 35) строится с помощью эпюры ω₀ (рис. 34).

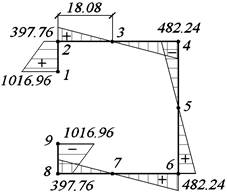
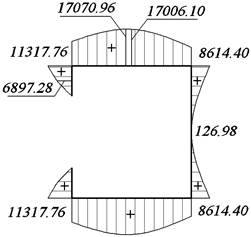
Рис. 34. Эпюра ω₀, см² Рис.35. Эпюра S_ω^отс , см³

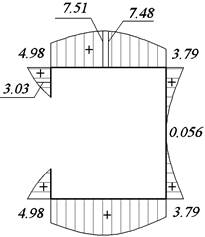
Рис. 36. Эпюра τ_ω, МПа

Касательные напряжения от изгибно-крутящего момента (рис. 36)

Находим напряжения от чистого кручения в опорном сечении (рис. 37)

Эпюра τ_ω построена с помощью эпюр ω₀ и . Эпюру τ (рис. 38) получаем суммированием эпюр τ_u, τ_ω и τ₀.

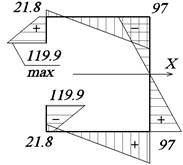
Наибольшие касательные напряжения τ:

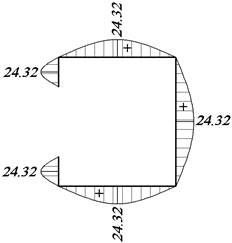
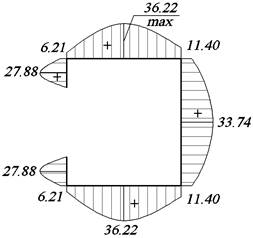
Рис. 37. Эпюра τ₀, Мпа Рис. 38. Эпюра τ, МПа

3.2.14. Нахождение угла закручивания

При

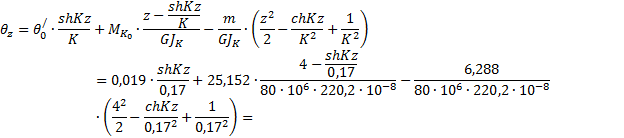
3.3. Пример №3

3.3.1. Исходные данные

В табл. 10 приведены исходные данные для примера №3. На рис. 39 и 40 даны поперечное сечение и расчетная схема рассматриваемого стержня.

Таблица 10. Исходные данные

В, см	24
Н, см	30
𝛿, см	1,4
F2 , кН	30
L, м	4
Е, ГПа	200
G, ГПа	80

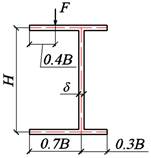
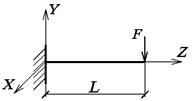
Рис. 39. Поперечное сечение Рис. 40. Расчетная схема

3.3.2. Определение положения центра тяжести, величины главных центральных моментов инерции поперечного сечения

Площадь поперечного сечения

Статический момент площади относительно оси Y₁

Координаты центра тяжести (рис. 40)

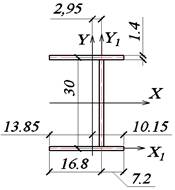
Рис. 40. Координаты центра тяжести

Для тонкостенных стержней моменты инерции J_x и J_y вычисляем перемножением эпюр линейных координат по правилу Верещагина (при помощи эпюр линейных координат рис. 41 и 42):

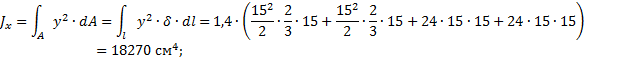
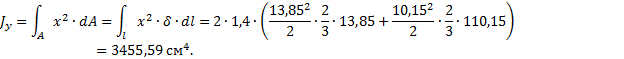
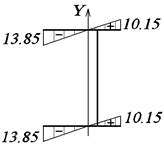
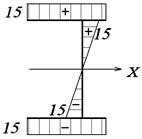
Рис. 41. Эпюра X, см Рис. 42. Эпюра Y, см

3.3.3. Определение координат центра изгиба

Для определения центра изгиба строим эпюру секториальных координат (рис. 43) с произвольным полюсом В и началом отсчета M₀. B и M₀ располагаем на контуре по оси симметрии сечения.

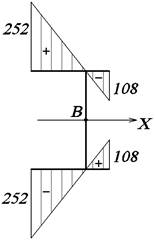
Рис. 43. Эпюра ω_В, см²

Секториальную координату определяем по формуле

Расположение точек взято с рис. 44.

Секториально-линейный статический момент относительно оси X вычисляем перемножением эпюр ω_B и Y по формуле

Определяем координаты центра изгиба

a_x откладываем от полюса B по оси Х, получаем центр изгиба А (рис. 44).

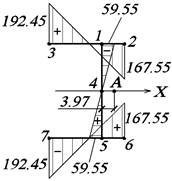
Рис. 44. Эпюра ω₀, см²

3.3.4. Построение эпюры главных секториальных координат поперечного сечения

Эпюру главных секториальных координат строим, располагая полюс в центре изгиба А.

Проверка правильности определения положения центра изгиба:

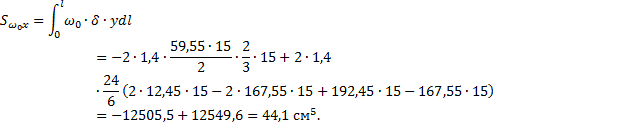
Эпюра ω₀ построена правильно, положение центра изгиба верное.

3.3.5. Вычисление момента инерции при чистом кручении J_K, секториального момента инерции J_ω0, изгибно-крутильной характеристики K

Для двутаврового сечения α=1,2.

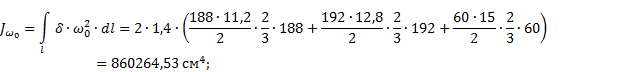
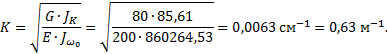
3.3.6. Определение неизвестных начальных параметров

На рис. 45 показан эксцентриситет е.

При z=L по табл. 5

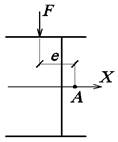
Рис. 45. Нахождение эксцентриситета

3.3.7. Определение ординат для построения эпюры бимоментов B_ω

По табл. 5

С шагом в 1 м длины балки определяем

3.3.8. Определение ординат для построения эпюры изгибно-крутящих моментов M_ω

По табл. 5

3.3.9. Определение ординат для построения эпюры моментов чистого кручения

По табл.5

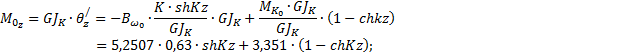
3.3.10. Определение ординат для построения эпюры внешних крутящих моментов

Результаты вычислений внутренних усилий сводим в табл.11.

Таблица 11. Внутренние усилия

z	Kz
0	0	-5,2995	3,351	0	3,351
1	0,63	-2,8093	3,351	1,5580	1,7930
2	1,26	-1,4715	3,351	2,3805	0,9705
3	1,89	-0,7374	3,351	2,8050	0,5460
4	2,52	-0,3057	3,351	3,0054	0,3456

3.3.11. Построение эпюр внутренних усилий (рис.46)

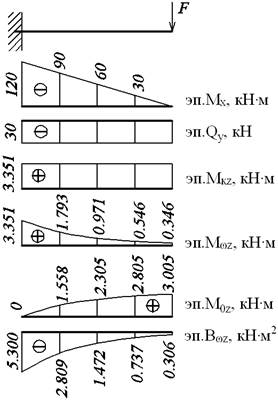
Рис. 46. Эпюры внутренних усилий

3.3.12. Построение эпюры нормальных напряжений в опасном сечении стержня

Нормальные напряжения

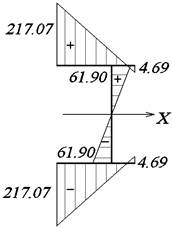
По эпюрам M_x и B_ω опасным сечением в консольной балке является опорное.

Эпюры σ_u и σ_ω построены с помощью эпюр Y и ω₀. Эпюру σ получаем суммированием эпюр σ_u и σ_ω (рис. 47, в).

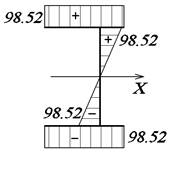
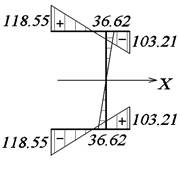
а б в

Рис. 47. Эпюры нормальных напряжений:

а – эпюра σ_u, МПа; б – эпюра σ_ω, МПа; в – эпюра σ, МПа

3.3.13. Построение эпюр касательных напряжений в опасном сечении стержня

Касательные напряжения

По эпюрам опасным является опорное сечение.

Определим касательные напряжения от изгиба (рис. 48).

где - статический момент отсеченной части сечения относительно оси Х.

Остальные ординаты симметричны найденным.

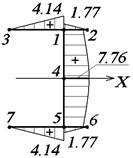
Рис. 48. Эпюра τ_u, МПа

Определение напряжения от изгибно-крутящего момента (рис. 49).

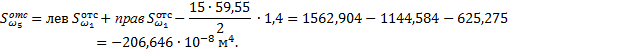
Эпюра τ_ω построена с помощью эпюр ω₀ и . Эпюру τ (рис. 50) получаем суммированием эпюр τ_u, τ_ω и τ₀.

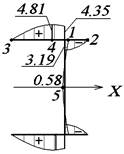
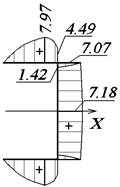
Рис. 49. Эпюра τ_ω, Мпа Рис. 50. Эпюра τ, МПа

Определим напряжения от чистого кручения в опорном сечении , так как на опоре .

3.3.14. Нахождение угла закручивания

---

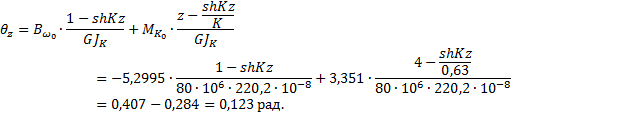
email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00