Главная
Лекция
15. Прочность при динамических
нагрузках
Содержание
Соударение твердого тела и системы
с одной степенью свободы
Механические испытания на удар
Расчет динамического
коэффициента при ударной нагрузке
Оценка прочности при ударной нагрузке
Определение напряжений при
скручивающем ударе
Расчёты движущихся деталей при
заданных ускорениях
Расчет поступательно
движущихся систем
Напряжения в тонкостенном
вращающемся кольце
Расчет равномерно
вращающегося прямого бруса
В предыдущих разделах рассматривалось такое нагружение конструкций, когда прикладываемые усилия изменялись настолько медленно, что возможно было считать их статическими. В инженерной практике же часто встречаются случаи, когда нагрузка достаточно быстро изменяет свое направление или величину, т.е. зависят от времени. Такое нагружение называется динамическим и вызывает значительные силы инерции в сооружении, которые приводят к появлению дополнительных (к статическим) напряжений и деформаций.
Известны случаи, когда инженерные конструкции, рассчитанные с большим запасом прочности на статическую нагрузку, разрушались под действием сравнительно небольших динамических сил. С целью избежания этих нежелательных явлений необходимо с особой тщательностью подходить к расчетам элементов конструкций, которые в данном случае более сложны, чем при статических нагрузках. Они требуют привлечения более сложных методов определения внутренних сил, учитывающих разнообразные воздействия динамической нагрузки, особенности сопротивляемости последним многих материалов. Так, при действии ударной нагрузки, характеризующейся чрезвычайно малой продолжительностью, многие материалы, которые при наличии статических сил проявляли себя пластичными, работают как хрупкие. В случае колебаний упругой системы многократно повторяющиеся нагрузки приводят к резкому снижению прочности материалов, связанному с усталостными явлениями.
Динамическое действие нагрузок, вызванное движением деталей машин или механизмов, а также элементов конструкций, учитывается при использовании расчетов, основанных на известном в механике твердого тела принципе Даламбера. Исходя из этого, если силы инерции известны, то расчет можно вести по методу сечений, а для вычисления внутренних сил использовать уравнения статики твердого тела. Если же определение сил инерции затруднительно или вообще невозможно, как, например, при ударном действии нагрузок, для вычисления динамических напряжений и деформаций используется закон сохранения энергии с привлечением основных положений из курса сопротивления материалов о потенциальной энергии деформируемого тела. В ряде случаев динамические напряжения во много раз превышают статические.
Задача соударения твердых деформируемых тел в механике, как правило, относится к классу динамических контактных задач со смешанными граничными условиями, содержащими в себе многие трудности математического порядка при их решении, которые не всегда могут быть преодолены простыми инженерными способами. Эти трудности в первую очередь связаны с определением с определением характера изменения функции напряжения в зоне контакта соударяемых тел по пространственным координатам и во времени. Большие сложности возникают и при учете волновых процессов, возникающих, как в зоне контакта, так и внутри соударяемых тел. Например, дифракционных волновых процессов по контуру в зоне контакта, и интерференционных явлений внутри соударяемых тел. Здесь существенное значение приобретает и учет фактора рассеяния энергии, трудно поддающийся анализу в данном случае.
Исходя из вышеизложенного, ниже при решении задач, применяется упрощенный инженерный подход, основанный на следующих упрощающих предпосылках: при взаимодействии соударяемых тел они принимаются или идеально упругими, или абсолютно твердыми. Деформации в упругих соударяемых телах происходят мгновенно.
Установлено, что практически во всех случаях силы динамического воздействия пропорциональны статическим, в связи с чем расчеты на прочность и жесткость при динамических нагрузках выполняются по методам, разработанным для статических, но с введением соответствующих значений динамических коэффициентов. Таким образом, учитывая это, имеем
где 
- динамический
коэффициент.
Условия прочности и жесткости применительно к расчету по методу допускаемых напряжений имеют соответственно вид
При изучении динамики упругих систем последние принято классифицировать, прежде всего, по числу их степеней свободы. Под числом степеней свободы понимается число независимых координат, определяющих положение материальных точек системы в произвольный момент времени.
Рис. 15.1
Так для системы, изображенной на рис. 15.1, если пренебречь массой стержней, положение сосредоточенной массы m в плоскости чертежа полностью будет определяться двумя независимыми координатами - линейными перемещениями в вертикальном и горизонтальном направлениях. То есть рассматриваемая система будет иметь две степени свободы. Заметим что, так как во всех реальных системах масса конструкции распределена по их объему, поэтому любая произвольно взятая точка является материальной. Следовательно, для определения положения системы в произвольный момент времени, строго говоря, необходимо знать перемещения всех точек рассматриваемой системы. Откуда следует, что все реальные системы в точной постановке задачи, имеют бесконечное число степеней свободы, так как число материальных точек, принадлежащей любой реальной системы, равно бесконечности.
Из различных задач динамики конструкций здесь рассматриваются задачи на действие инерционных и ударных нагрузок, а также задачи на упругие свободные колебания систем с одной степенью свободы.
Соударение твердого тела и системы с одной степенью свободы
Задача соударения различных механических систем часто встречается в инженерной деятельности в различных сферах, поэтому имеет большое практическое значение.
Взаимодействие тел, при котором за очень малый промежуток времени скачкообразно изменяются скорости взаимодействующих тел, называется ударом. В период взаимодействия соударяемых тел между ними развивается результирующая контактная сила. Хотя время действия контактной силы обычно очень мало и измеряется микро- или миллисекундами, она развивается очень быстро и принимает большие значения.
При забивке
свай тяжелый груз падает с некоторой высоты на верхний торец сваи и погружает
ее в грунт; баба останавливается почти мгновенно, вызывая удар. Аналогичные
явления происходят при ковке; удар испытывают и
проковываемое изделие и шток молота с бойком, так как последний очень быстро
останавливается при соприкосновении с изделием. Во время удара между обеими
ударяющимися деталями возникают весьма большие взаимные давления. Скорость
ударяющего тела за очень короткий промежуток времени изменяется и в частном
случае падает до нуля; тело останавливается. Значит, на него от ударяемой
детали передаются очень большие ускорения, направленные в сторону, обратную его
движению, т. е. передается реакция 
,
равная произведению массы ударяющего тела на это ускорение.
Обозначая это
ускорение через а, можно написать,
что реакция 
,
где Q — вес ударяющего тела. По
закону равенства действия и противодействия на ударяемую.
часть конструкции передается такая же сила, но обратно
направленная (рис.15.2). Эти силы и вызывают напряжения в обоих телах.
Рис.15.2
Таким образом,
в ударяемой части конструкции возникают такие напряжения, как будто к ней была
приложена сила инерции ударяющего тела; мы можем вычислить эти напряжения,
рассматривая силу инерции как статическую нагрузку нашей конструкции.
Затруднение заключается в вычислении этой силы инерции. Продолжительности
удара, т. е. величины того промежутка времени, в течении
которого происходит падение скорости до нуля, мы не знаем. Поэтому остается
неизвестной величина ускорения а, а
стало быть, и силы .
Таким образом, хотя вычисление напряжений при ударе представляет собой частный
случай задачи учета сил инерции, однако для вычисления силы и связанных с ней напряжений и деформаций
здесь приходится применять иной прием и пользоваться законом сохранения
энергии.
При ударе
происходит очень быстрое превращение одного вида энергии в другой: кинетическая
энергия ударяющего тела превращается в потенциальную энергию деформации.
Выражая эту энергию в функции силы или напряжений, или деформаций получаем
возможность вычислить эти величины.
В зависимости от скорости приложения контактной силы, ударное нагружение может рассматриваться как квазистатическое или ударное. В случае ударного нагружения необходимо учитывать не только величину нагрузки, но и время, в течение которого она достигает конечного значения, и импульс, представляющий собой площадь под кривой зависимости нагрузки от времени. При действии ударных нагрузок не только повышаются напряжения по сравнению с квазистатическим нагружением, но и могут значительно меняться свойства материала – возрастают предел текучести и предел прочности материала и снижается его пластичность, т.е. происходит охрупчивание материала.
Теория удара опирается на некоторые допущения: форма изогнутой оси
балки при ударе подобна изогнутой оси балки при статическом ее нагружении;
считают, что удар является неупругим, то есть ударяющее тело не отскакивает от
конструкции, а продолжает двигаться вместе с ней; считают, что деформации,
вызванные ударом, являются упругими, то есть 
; массой балки пренебрегают, то есть считают балку невесомой.
Механические испытания на удар
Обычные ударные испытания образцов, осуществляемые на маятниковых копрах, призваны оценить склонность материала к хрупкому разрушению и относятся по своим скоростным показателям (скорость удара 5-7 м/с) к квазистатическому нагружению. Ниже будет рассмотрено поведение металлических материалов при квазистатическом ударном нагружении. Метод основан на разрушении при изгибе образца с концентратором в виде надреза одним ударом маятника копра. Надрез в стандартных образцах облегчает хрупкое разрушение материалов. В результате испытания определяют полную работу, затраченную при ударе на разрушение образца (работу удара) K, и ударную вязкость KC. Под ударной вязкостью следует понимать работу удара, отнесенную к начальной площади поперечного сечения образца в месте концентратора. Единицей измерения ударной вязкости является Дж/см2.
В зависимости от вида концентратора (U-, V или T-образный надрез) ударная вязкость обозначается как KCU, KCV или KCT. Выбор вида концентратора осуществляется в зависимости от требований к изделию: U - при обычных испытаниях металлов и сплавов; V - для конструкций повышенной степени надежности (летательные аппараты, транспортные средства, трубопроводы, сосуды давления); T - для особо отвестственных конструкций.
Для определения вязкости хрупких материалов (инструментальных сталей с твердостью более 50 HRC) применяют гладкие образцы и ударная вязкость обозначается KC.
Обычно испытывается призматический образец квадратного сечения 10х10 мм и длиной 55 мм с краевым надрезом глубиной 2 мм в середине образца. На рис.15.3 представлена схема нагружения образца при испытании его на удар.
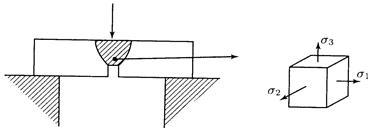
Рис.15.3
В зоне концентрации напряжений происходит локализация деформации, и возникает объемное растяжение, вследствие стеснения деформации в поперечном направлении. Это в сочетании с высокой скоростью деформирования (порядка 102 1/с) способствует проявлению хрупкости материала. Хотя ударная вязкость как свойство материала носит условный характер, она оказалась весьма чувствительной к особенностям структуры материала и механического его поведения. Например, различие в комплексе свойств при деформировании и разрушении мелкозернистого и крупнозернистого железа четко выявляется ударной вязкостью, тогда как статические характеристики этого не отражают (табл.15.1).
Таблица 15.1
|
Структура железа |
|
|
|
|
KCV, Дж/см2 |
|
Мелкозернистая |
268 |
375 |
35,3 |
72,2 |
13,1 |
|
Крупнозернистая |
185 |
345 |
36,9 |
66,7 |
2,6 |
Испытанию на удар подвергаются практически все материалы. При поставках
металла ударная вязкость является настолько же обязательной характеристикой
металла, как 
,
и 
.
Она характеризует способность материала сопротивляться хрупкому разрушению (поглощать
энергию удара за счет пластического деформирования) при заданной температуре
испытания. В таблице 15.2 приведены значения ударной вязкости для углеродистых
сталей.
Таблица 15.2 Ударная вязкость некоторых сталей
|
Содержание в стали углерода |
Термообработка |
|||
|
отжиг |
закалка и отпуск |
|||
|
|
KCV, Дж/см2 |
|
KCV, Дж/см2 |
|
|
0,15 |
350-450 |
2,5 |
360-500 |
2,5 |
|
0,15-0,20 |
400-500 |
2,2 |
450-650 |
2,0 |
|
0,20-0,30 |
500-600 |
2,0 |
550-750 |
1,5 |
|
0,30-0,40 |
600-700 |
1,6 |
700-850 |
1,2 |
|
0,40-0,50 |
700-800 |
1,2 |
800-950 |
0,9 |
|
0,50-0,60 |
800-900 |
1,0 |
900-1050 |
0,5 |
|
0,60-0,70 |
850-950 |
0,8 |
1000 |
0,3 |
|
0,70 |
950 |
0,6 |
1050 |
0,2 |
Ударная вязкость металла существенно зависит от температуры испытания. Это особенно относится к металлам и сплавам с о.ц.к. решеткой, состояние которых изменяется с понижением температуры от вязкого к хрупкому. Испытания показывают, что при понижении температуры сначала наблюдается постепенное снижение ударной вязкости, при определенной температуре она достигает своего наименьшего значения, которое при дальнейшем понижении температуры не изменяется.
Температуры 
и 
называют соответственно верхней и нижней
температурами хрупкости, а само явление хладноломкостью.
Порог хладноломкости определяется типом кристаллической решетки, количеством
примесей внедрения, при этом зависимость наблюдается обратная – чем ниже порог
хладноломкости, тем выше ударная вязкость, т.е. ударная вязкость
есть функция порога хладноломкости.
Для металла в хрупком состоянии характерны низкие значения ударной вязкости, мало изменяющиеся в широком диапазоне изменения температуры (так называемое «нижнее плато» значений ударной вязкости). При вязком состоянии характерны высокие значения ударной вязкости («верхнее плато»). Переход из одного состояния в другое происходит в определенном температурном интервале – температурном интервале хрупко-вязкого перехода.
Для объяснения
перехода металлов из хрупкого состояния в вязко-пластичное
привлекается известная схема А.Ф.Иоффе, которая учитывает особенности
деформирования и разрушения металлических материалов: возможность разрушения
путем отрыва (хрупкий характер разрушения) и путем среза (вязкий характер
разрушения). Отмечается слабая зависимость сопротивления отрыву 
от температуры при значительном разбросе этой
характеристики и существенное снижение сопротивления течению 
и сопротивления срезу 
с повышением температуры (рис.15.4).
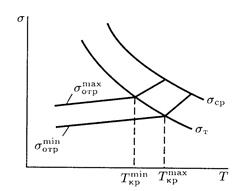
Рис.15.4
Указанное
изменение характеристик прочности и пластичности предопределяют суммарное
изменение ударной вязкости, например KCV, в зависимости от температуры в весьма жестких условиях
нагружения, когда довольно четко выявляется так называемая критическая
температура хрупкости, или температура хрупко-вязкого перехода 
.
У разных материалов проявляются свои особенности хрупко-вязкого перехода:
скачкообразный переход при определенной температуре (рис.15.5, а);
наличие области разброса KCV
в пределах экстремальных значений, определяющей интервал хрупко-вязкого
перехода 
(рис. 15.5, б); суженная область разброса KCV в определенном интервале температур (рис. 15.5, в).
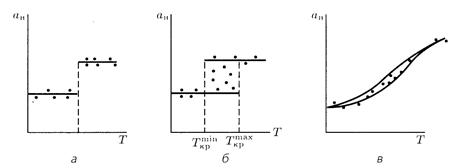
Рис.15.5
Хрупко-вязкий
переход проявляется в изменении характера излома от хрупкого к вязкому, который также происходит в определенном
температурном интервале. В качестве критерия для определения обычно используются сразу два показателя:
уровень ударной вязкости KCV в зависимости от предела текучести материала и процент
вязкой фазы в изломе. Например, для материалов энергетического оборудования обусловлена определенным уровнем KCV для
конкретного материала и не менее 50% вязкой фазы в изломе
при температуре +30 0С. Следует отметить, что
критическая температура хрупко-вязкого перехода – одна из основных комплексных
механических характеристик малоуглеродистых и низколегированных сталей. Следует
добиваться использования материала в температурной области, где проявляется
вязкий характер его разрушения.
Расчет динамического коэффициента при ударной нагрузке
Предположим, что очень жесткое тело А весом Q, деформацией которого можно пренебречь, падая с некоторой высоты H, ударяет по другому телу B, опирающемуся на упругую систему С (рис.15.6). В частном случае это может быть падение груза на конец призматического стержня, другой конец которого закреплен (продольный удар), падение груза на балку, лежащую на опорах (изгибающий удар), и т. п.
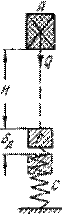
Рис.15.6
В течение
очень короткого промежутка времени упругая система С испытает некоторую деформацию.
Обозначим через 
перемещение тела В (местной деформацией которого пренебрежем) в направлении удара. В
упомянутых частных случаях при продольном ударе за перемещение соответственно нужно считать продольную
деформацию стержня 
,
при изгибающем ударе — прогиб балки 
в ударяемом сечении и т. п. В результате
удара в системе С возникнут
напряжения 
(
или
— в зависимости от вида деформации).
Полагая, что
кинетическая энергия Т ударяющего тела полностью переходит в
потенциальную энергию 
деформации упругой системы, можем написать:
Так как к
моменту окончания деформации ударяющее тело пройдет путь H+,
то его запас энергии будет измеряться произведенной им работой 
и будет равен:
Вычислим
теперь .
При статической деформации потенциальная энергия 
численно равна половине произведения
действующей силы на соответствующую деформацию:
Статическая
деформация 
в ударяемом сечении может быть вычислена по
закону Гука, который в общем виде можно записать так:
или 
Здесь с — некоторый коэффициент
пропорциональности (называемый иногда жесткостью системы); он зависит от
свойств материала, формы и размеров тела, вида деформации и положения
ударяемого сечения. Так, при простом растяжении или сжатии 
,
и 
;
при изгибе балки, шарнирно закрепленной по концам, сосредоточенной силой Q посредине пролета 
и 
;
и т.д.
Таким образом, выражение для энергии может быть переписано так:
В основу этой формулы
положены две предпосылки: а) справедливость закона Гука и б) постепенный — от
нуля до окончательного значения — рост силы Q,
напряжений 
и пропорциональных им деформаций .
Опыты с определением
модуля упругости по наблюдениям над упругими колебаниями стержней показывают,
что и при динамическом действии нагрузок закон Гука остается в силе, и модуль
упругости сохраняет свою величину. Что касается характера нарастания напряжений
и деформаций, то и при ударе деформация происходит, хотя и быстро, но не
мгновенно; постепенно растет в течение очень короткого
промежутка времени от нуля до окончательного значения; параллельно росту
деформаций возрастают и напряжения 
.
Реакция
системы С на действие упавшего груза Q (назовем ее 
)
является следствием развития деформации ;
она растет параллельно от нуля до окончательной, максимальной
величины и, если напряжения не превосходят предела пропорциональности
материала, связана с ней законом Гука:
где с — упомянутый выше коэффициент пропорциональности, сохраняющий свое значение и при ударе.
Таким образом,
обе предпосылки для правильности формулы (15.6) принимаются и при ударе.
Поэтому можно считать, что вид формулы для при ударе будет тот же, что и при статическом
нагружении системы С силой инерции ,
т. е.
(Здесь учтено,
что по предыдущему 
)
Подставляя значения Т
и в уравнение (15.4), получаем:
или
Отсюда
или, удерживая перед радикалом для определения наибольшей величины деформации системы в направлении удара знак плюс, получаем:
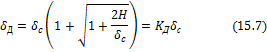
Так как напряжения и усилия по закону Гука пропорциональны деформации, то
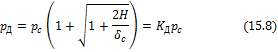
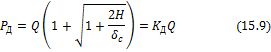
Из этих формул видно, что величина динамических деформаций, напряжений и усилий зависит от величины статической деформации, т.е. от жесткости и продольных размеров ударяемого тела; ниже это дополнительно будет показано на отдельных примерах. Величина
в данном случае представляет собой динамический коэффициент.
В случае
внезапного приложения груза, когда H=0 получаем 
.
Формула (15.10) используется в случаях, когда масса упругого тела, испытывающего удар, мала и ею в расчете пренебрегают.
При необходимости учета массы тела, испытывающего удар, формула для расчета динамического коэффициента принимает вид
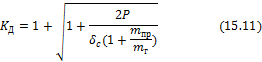
где mг – масса падающего груза, mпр – приведенная масса тела, испытывающего удар, причем
где m – истинная (распределенная) масса тела; 
– коэффициент
приведения распределенной массы к точечной. Он определяется путем
сравнения кинетической энергии тела с распределенной и с точечной массами.
Коэффициент зависит от вида удара (продольный, изгибный и
т.п.) и от характера закрепления концов стержня.
Так, для
консольной балки, испытывающей продольный удар (рис. 15.7, а), 
;
для шарнирно опертой балки на двух опорах, испытывающей удар посередине (рис.
15.7, б), 
;
для консольной балки, испытывающей изгибный удар (рис. 15.8, в), 
и т.д.
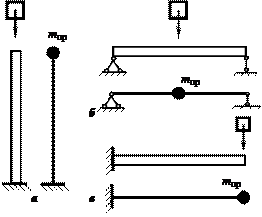
Рис.15.7
Заменяя в этой
формуле Н на 
,
где v —
скорость ударяющего тела в начальный момент удара, получаем:
Кроме того, так как
где 
— энергия ударяющего тела к моменту начала
удара, то выражение для динамического коэффициента может быть представлено еще
и в таком виде:
Если мы в
формулах (15.7) и (15.8) положим H=0, т.е. просто сразу приложим груз Q, то 
и 
;
при внезапном приложении силы Q
деформации и напряжения вдвое больше, чем при статическом действии той же силы.
Наоборот, если
высота падения груза Н (или скорость v) велика по сравнению с деформацией ,
то в подкоренном выражении формул (15.7) — (15.13) можно пренебречь единицей по
сравнению с величиной отношения 
.
Тогда для и получаются следующие выражения:
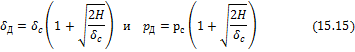
При очень
большой величине отношения можно пренебречь и единицей, стоящей перед
корнем, т.е. написать:
Динамический коэффициент в этом случае определяется по формуле
Необходимо
отметить, что в то время как пренебрежение единицей 2Н в подкоренном выражении допустимо уже при 
(неточность приближенных формул будет не
больше 5%). Пренебрежение единицей, стоящей перед корнем, допустимо лишь при
очень большой величине отношения .
Так, например,
для того чтобы приближенные формулы (15.16) и (15.17) давали погрешность не
более 10%, отношение должно быть больше 110.
Формулы 
и 
,
в которых 
выражается через 
,
могут быть использованы также для решения задачи о встречном ударе тел,
двигающихся с некоторой скоростью, при определении напряжений в цилиндре
двигателя внутреннего сгорания, вызванных резким повышением давления газа при
вспышке горючей смеси и др. На этом основании их можно считать общими формулами
для расчета на удар.
Обобщая сказанное выше, можем наметить следующий общий прием решения задач на определение напряжений при ударе. Применяя закон сохранения энергии, надо:
1) вычислить кинетическую энергию ударяющего тела Т;
2) вычислить потенциальную
энергию тел, воспринимающих удар, под нагрузкой их
силами инерции при ударе; потенциальная энергия должна быть выражена через
напряжение (
)
в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу
инерции ударяющего тела;
3) приравнять
величины и Т
и из полученного уравнения найти или непосредственно динамическое напряжение,
или деформацию, а по ней, пользуясь законом Гука, напряжение или силу и соответствующие ей динамические напряжения и
деформации.
Описанный общий прием расчета на удар предполагает, что вся кинетическая энергия ударяющего тела целиком переходит в потенциальную энергию деформации упругой системы. Это предположение не точно. Кинетическая энергия падающего груза частично превращается в тепловую энергию и энергию неупругой деформации основания, на которое опирается система.
Вместе с тем при высоких скоростях удара деформация за время удара не успевает распространиться на весь объем ударяемого тела и в месте удара возникают значительные местные напряжения, иногда превосходящие предел текучести материала. Так, например, при ударе свинцовым молотком по стальной балке большая часть кинетической энергии превращается в энергию местных деформаций. Подобное же явление может иметь место даже и в том случае, когда скорость удара мала, но жесткость или масса ударяемой конструкции велика.
Указанный
случай соответствуют большим величинам дроби .
Поэтому можно сказать, что описанный выше метод расчета применим, пока дробь не превышает определенной величины. Более
точные исследования показывают, что ошибка не превышает 10%
если 
.
Так как эта дробь может быть представлена в виде отношения ,
то можно сказать, что изложенный метод применим, пока энергия удара превышает
не более чем в 100 раз потенциальную энергию деформации, соответствующую
статической нагрузке конструкции весом ударяющего груза. Учет массы ударяемого
тела при ударе позволяет несколько расширить пределы применимости этого метода
в тех случаях, когда масса ударяемого тела велика.
Более точная теория удара излагается в курсах теории упругости.
Оценка прочности при ударной нагрузке
Вид формул, полученных для динамического коэффициента, показывает, какие большие качественные различия ведет за собой количественное изменение периода действия силы на тело.
Рассмотрим некоторые случаи удара при простейших деформациях. При этом для нахождения коэффициента динамичности применим основные полученные формулы для динамического коэффициента.
Для
определения 
используем зависимости:
В случае продольного растягивающего или сжимающего удара (рис.15.8)
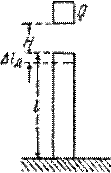
Рис.15.8
Для вычисления
динамического коэффициента может быть выбрано одно из следующих
выражений:
После этого
без затруднений вычисляются 
.
Приближенная формула для вычисления напряжений в данном частном случае получает такой вид:
Замечаем, что как при статической, так и при динамической нагрузке напряжение в сжатом стержне зависит от величины сжимающей силы и от площади поперечного сечения стержня.
Но при
статическом действии груза Q
передающаяся на стержень сила равна Q
и не зависит от размеров и материала стержня, при ударе же величина силы ,
вызывающей напряжения в стержне, зависит от ускорения, передающегося от
ударяемого тела на ударяющее, т.е. от величины промежутка времени, в течение
которого изменяется скорость ударяющего тела. В свою очередь этот промежуток
времени зависит от величины динамической продольной деформации ,
от податливости стержня. Чем эта величина больше, т. е. чем меньше модуль Е и чем больше длина стержня 
, тем больше продолжительность удара, меньше ускорение и
меньше давление .
Таким образом, при равномерном распределении напряжений, одинаковом во всех сечениях стержня, динамическое напряжение будет уменьшаться с увеличением площади поперечного сечения стержня и с увеличением его податливости (т. е. с увеличением длины и уменьшением модуля упругости Е); именно поэтому смягчают удар всякие рессоры и пружины, расположенные между ударяющимися деталями. Все это и отражают приведенные выше формулы. В частности, с известным приближением можно считать, что при продольном ударе величина напряжений зависит уже не от площади, а от объема стержня.
Вычислив величину динамического напряжения, мы можем теперь написать условие прочности в виде
где 
- допускаемая величина нормальных напряжений
при ударе, равная для пластичного материала 
.
Величину
коэффициента запаса 
можно было бы выбрать равной величине
основного коэффициента запаса 
при статическом действии нагрузок, так как
динамичность нагрузки уже отражена. Однако, ввиду некоторой упрощенности
изложенного метода расчета, этот коэффициент принимают несколько повышенным — до 2. Кроме того, обычно в этих случаях
применяют материал более высокого качества (в отношении однородности и
пластических свойств).
При изгибе
величина статической деформации ,
представляющей собой статический прогиб балки с 
в месте удара,
зависит от схемы нагружения и условий опирания балки.
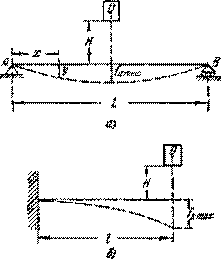
Рис.15.9
Так например, для балки пролетом l, шарнирно закрепленной по концам и испытывающей посредине пролета удар от падающего с высоты Н груза Q (рис.15.9, а), получаем:
для консоли, испытывающей удар от груза Q, падающего на свободный конец консоли (рис. 15.9, б):
Подставляя в формулу
для коэффициента динамичности значения 
или ,
находим ,
а затем и величину динамических напряжений и деформаций. Так например, в случае
балки на двух опорах при вычислении динамического напряжения 
имеем такую формулу:
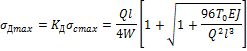
Условие прочности в этом случае напишется:
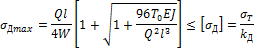
Приближенные
формулы для вычисления 
и в случае удара по балке на двух опорах
получают такой вид:
Аналогичные
выражения для и получаются и в случае удара по консоли. Имея в
виду, что
и
можем
представить выражение для еще и в таком виде:
Из последней
приближенной формулы видно, что динамические напряжения при изгибе балки
зависят от модуля упругости материала, объема балки, формы ее поперечного
сечения (отношение 
),
а также от схемы нагружения и условий опирания балки (в данном случае в
подкоренном выражении стоит 6Т0;
для балок, иначе загруженных и закрепленных, числовой коэффициент у Т0
будет другим). Таким образом, в балке прямоугольного сечения высотой h и шириной b, поставленной на ребро или положенной плашмя, наибольшие
напряжения при ударе будут одинаковы и равны (по приближенной формуле):
так как в обоих случаях
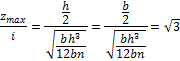
Как известно, при одинаковой статической нагрузке наибольшие напряжения в балке, положенной плашмя, будут в отношении h/b больше, чем напряжения в балке, поставленной на ребро. Сказанное выше, разумеется, справедливо лишь до тех пор, пока явление удара происходит в пределах упругости.
Сопротивление балок ударным нагрузкам зависит и от момента сопротивления и от жесткости балки. Чем больше податливость, деформируемость балки, тем большую живую силу удара она может принять при одних и тех же допускаемых напряжениях. Наибольший прогиб балка дает в том случае, когда во всех ее сечениях наибольшие напряжения будут одинаковыми, т. е. если это будет балка разного сопротивления; такие балки при одном и том же допускаемом напряжении дают большие прогибы, чем балки постоянного сечения, и значит, могут поглощать большую энергию удара. Поэтому рессоры обычно и делают в форме балок равного сопротивления.
Динамические
напряжения не должны превышать предел пропорциональности. Если все же
динамические напряжения оказались больше предела пропорциональности, необходимо
предусмотреть конструктивные меры по увеличению статического перемещения,
например, сделать опорные закрепления балки (рамы) податливыми, поставив
специальные прокладки. Увеличение приведет к уменьшению динамического
коэффициента (Попытки уменьшить динамические напряжения, увеличив размер
сечения, не проносят нужного эффекта, т.к. при увеличении размера сечения
увеличивается жесткость, статический прогиб уменьшается, а динамический
коэффициент увеличивается).
Пример
1.
В котором из двух одинаковых стержней, отличающихся только материалом возникнут большие динамические напряжения (рис.15.10)?
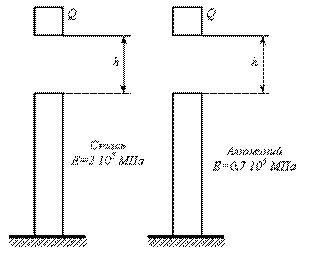
Рис. 15.10
Таким образом,
и динамические напряжения больше в стальном
стержне.
Пример
2.
В котором из двух стержней, сделанных из одного материала возникнут большие динамические напряжения (рис. 15.11)?
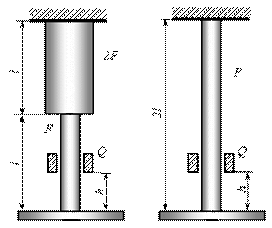
Рис. 15.11
В данном случае имеет место продольный растягивающий удар. Перемещение нижнего концевого сечения от статически приложенной силы Q будет
а второго стержня
Следовательно,
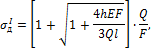
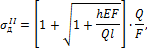
то есть напряжения в первом стержне больше, чем во втором.
Пример
3.
Определить максимальные динамические напряжения при вертикальном ударе, а также динамический прогиб балки в точке D (рис. 15.12).
Грузовая эпюра изгибающих моментов (Mp) от статически приложенного груза Q и эпюры изгибающих моментов от единичных сил, приложенных в точке удара (M1) и в точке D (M1/), построены на рис. 15.12.
Рис. 15.12
Максимальные динамические напряжения будут действовать в сечении правой опоры в месте действия максимального изгибающего момента
где
а 
есть статический прогиб балки под падающим грузом,
то есть прогиб в точке C. Для
определения этого перемещения воспользуемся правилом
Верещагина:
Таким образом, имеем
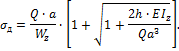
Динамический прогиб в точке D равен:
а статический прогиб в точке D определяем с помощью правила «дирижера»
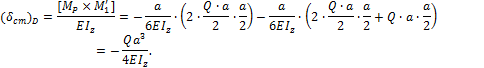
Знак минус означает, что точка D перемещается вверх. Окончательно имеем
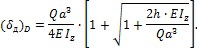
Определение напряжений при скручивающем ударе
Если вращающийся вал внезапно останавливается торможением одного из его концов, а на другом его конце на него передается живая сила маховика T0, скручивающая вал, то напряжения также могут быть определены указанным выше методом. Вал будет скручиваться двумя парами сил (силы инерции маховика и силы торможения) с моментом М.
В данном случае
и
Следовательно,
и
так как
Имея в виду, что живая сила маховика T0 равна
где 
— момент инерции массы маховика, а 
— угловая скорость, можем написать:
Замечаем, что и при скручивающем ударе наибольшие напряжения зависят от модуля упругости и от объема вала.
Расчёты движущихся деталей при заданных ускорениях
Определение напряжений и перемещений при заданных ускорениях основано на приведении задач динамики к задачам статики с помощью известного из курса теоретической механики принципа Даламбера (метода кинетостатики). Напомним, что этот принцип состоит в следующем: если в любой момент времени к каждой материальной точке данной системы приложить силу инерции этой точки, то эти силы инерции будут уравновешиваться заданными силами, действующими на систему, и реакциями связей, т.е. система может рассматриваться как находящаяся в состоянии покоя (или равномерного прямолинейного движения). Сила инерции равна произведению массы материальной точки на её ускорение и направлена в сторону, противоположную ускорению.
Расчет поступательно движущихся систем
Определим напряжения в канате грузоподъемного механизма, к которому подвешен груз массой m (рис. 15.13).
При
равномерном подъеме с постоянной скоростью ускорение движения груза равно нулю,
поэтому напряжения в канате такие же, как и в том случае, когда груз висит на
канате в состоянии покоя, т.е. 
,
где g - ускорение силы тяжести.
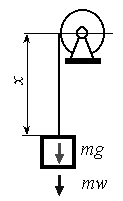
Рис. 15.13
Во время разгона движение груза неравномерно, и в канате появляются дополнительные напряжения, для определения которых мысленно остановим груз и приложим к нему силу инерции. Эта сила направлена в сторону, противоположную движению груза и равна
где v - скорость подъема; w - ускорение.
Наибольшее усилие в канате соответствует моменту максимального ускорения груза во время разгона:
Следовательно, максимальное напряжение в канате при подъеме груза
больше
напряжений при статическом приложении груза 
в 
раз; коэффициент
называется динамическим коэффициентом.
Таким образом,
для уменьшения растягивающего усилия в канате необходимо обеспечить плавное увеличение
скорости подъема, так как при больших ускорениях напряжения в канате могут
стать значительными. График изменения скорости в период разгона должен иметь
вид, представленный на рис. 15.14. Тангенс наибольшего угла наклона касательной к этой кривой определяет
максимальное ускорение движения груза во время подъема.
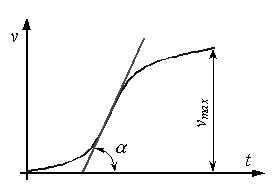
Рис. 15.14
При опускании
груза в начале движения величина w=dv/dt в выражении для
будет иметь отрицательный знак. Следовательно,
напряжения в канате в этом случае будут меньше напряжений от статического
действия груза m.
Если канат длинный, то следует учесть массу самого каната и силы инерции его частиц. В этом случае опасным будет верхнее сечение каната, усилие в котором
где x - длина каната; 
- плотность материала каната.
Рассмотрим горизонтальный брус, поднимаемый вверх силой S, приложенной посредине бруса (рис. 15.15, а).
Интенсивность полной
погонной нагрузки, состоящей из собственного веса q бруса и инерционной нагрузки 
,
определяется по формуле (рис. 15.15, б, в)
или
где G - вес бруса, w - ускорение бруса.
Рис. 15.15
Сила S и нагрузка qсумм вызывают изгиб бруса. Эпюры изгибающих моментов M и поперечных сил Q показаны на рис. 15.15, г, д.
Напряжения в тонкостенном вращающемся кольце
Рассмотрим
случай вращения тонкостенного кольца (
)
с постоянной угловой скоростью вокруг оси, перпендикулярной к плоскости
кольца (рис. 15.16, а).
При вращении
кольца каждый его элемент движется с центростремительным ускорением 
.
Силы инерции направлены в сторону, противоположную ускорениям, и при постоянном
сечении распределены равномерно вдоль кольца. Интенсивность сил инерции, т.е.
сила инерции, приходящаяся на единицу длины кольца, 
.
Здесь - плотность материала, F - площадь сечения, а R
- радиус средней линии кольца.
Кольцо теперь можно рассматривать как неподвижную плоскую раму, нагруженную равномерно распределенными радиальными силами интенсивностью q.
Рассекая кольцо любой диаметральной плоскостью на две части, приложим в сечениях осевые силы N и изгибающие моменты X1.
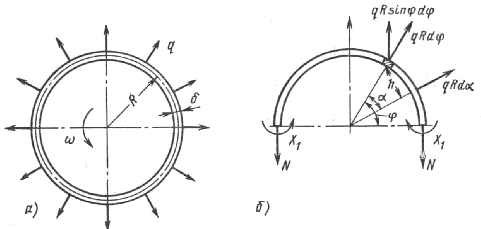
Рис. 15.16
Проектируя все силы, действующие на полукольцо, на направление оси y, получаем
Отсюда
N=qR.
Подставляя в это выражение значение q, находим
Для определения неизвестного X1 составим каноническое уравнение
коэффициенты
которого вычислим способом Мора.
Изгибающий момент в текущем сечении полукольца от силы N и распределенной нагрузки q (см. рис. 15.16, б)
а от единичной
пары 
Следовательно,
и поэтому X1=0,
т.е. изгибающие моменты во всех поперечных сечениях кольца равны нулю. Этот результат
объясняется тем, что при вращении вокруг центра кольцо сохраняет свою форму и
никаких изгибных деформаций не испытывает; увеличивается только его диаметр.
Таким образом, нормальные напряжения в поперечном сечении кольца
Например, в стальном кольце (=7850
кг/м3) радиуса R=50 см при
n=2500 об/мин растягивающее напряжение
Итак,
напряжения во вращающемся кольце зависят только от окружной скорости 
и плотности материала, но не зависят от
площади его поперечного сечения. Поэтому увеличением размеров сечения нельзя
уменьшить напряжения в тонкостенном вращающемся кольце.
Рассмотрим теперь случай равномерного вращения тонкостенного кольца вокруг его горизонтальной оси x.
Различные элементы кольца находятся на разных расстояниях от оси вращения, и поэтому силы инерции распределены неравномерно по длине кольца (рис. 15.17, a):
Максимальная
интенсивность 
.
Следовательно,
В сечениях вдоль вертикальной оси симметрии кольца будут действовать только изгибающие моменты X1, а перерезывающие силы Q и нормальные силы N равны нулю. В отсутствии нормальных сил N в этих сечениях легко убедиться, спроектировав все силы, действующие на левое или правое полукольцо, на горизонтальную ось симметрии.
Представим эквивалентную систему, как показано на рис. 15.17, б. Изгибающий момент в текущем сечении кольца от внешней нагрузки
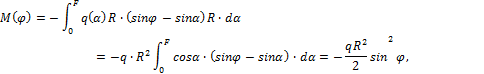
а от единичной
пары 
.
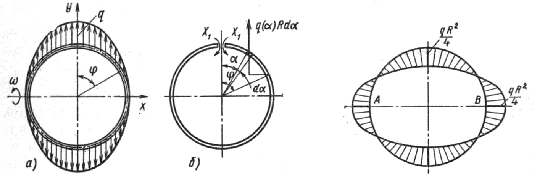
Рис. 15.17 Рис. 15.18
Составим каноническое уравнение
Коэффициенты 
и 
этого уравнения:
Следовательно,
Итак, изгибающий момент в текущем сечении рамы
Эпюра
изгибающих моментов представлена на рис. 15.18. Опасными являются сечения A и B
кольца, так как в этих сечениях кроме изгибающих моментов 
действуют наибольшие растягивающие нормальные
силы
Максимальные напряжения в раме
где 
- момент сопротивления изгибу, а F - площадь поперечного сечения кольца.
Расчет равномерно вращающегося прямого бруса
Предположим, что прямой брус постоянного поперечного сечения с подвешенным грузом равномерно вращается вокруг оси, перпендикулярной плоскости чертежа (рис. 15.19). Определим напряжения в сечениях бруса.
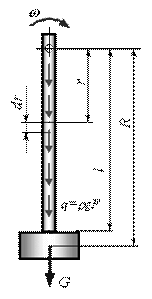
Рис. 15.19
При отсутствии вращения напряжения в поперечных сечениях бруса изменяются по линейному закону:
где - плотность материала бруса; F - площадь поперечного сечения; G - вес груза.
Применяя принцип Даламбера, приложим к каждому элементу бруса силу инерции, равную массе этого элемента, умноженной на его центростремительное ускорение. Динамическая продольная сила будет равна:
После интегрирования динамически напряжения определяются по следующей формуле:
Напряжения изменяются по квадратичному закону и достигают максимума на оси вращения
Перемещение текущего сечения бруса
Полагая в этом выражении r=1, находим удлинение всего бруса, вызванное его вращением.
При отсутствии груза следует исключить в формулах величину G.
При вращении стержня относительно вертикальной оси (рис. 15.20) полученные выше формулы для динамических усилий, напряжений и перемещений нетрудно модифицировать. Так, например, динамические напряжения будут равны:
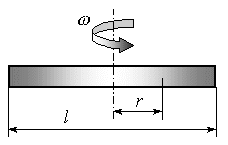
Рис. 15.20
Вращающиеся рамы
Рассмотрим несколько примеров расчета вращающихся рам.
Стержень
регулятора с прикрепленным к нему грузом массой Q вращается вокруг оси О-О
(рис. 15.21, а) с постоянной угловой
скоростью 
.
Построим эпюру изгибающих моментов, полагая, что масса рамы мала по сравнению с
массой груза.
Сила инерции
груза 
.
Рассматривая силу инерции груза как единственную внешнюю нагрузку на брус, строим эпюру изгибающих моментов (рис. 15.21, б). Максимальный изгибающий момент
Рис. 15.21
Рассмотрим
более сложный пример. Прямоугольная рама постоянного сечения (рис. 15.22, а) вращается вокруг вертикальной оси
симметрии с угловой скоростью
.
Определим изгибающие моменты в сечениях рамы, вызванные ее вращением.
На
горизонтальных элементах рамы интенсивность сил инерции изменяется по линейному
закону 
.
На вертикальных элементах интенсивность инерционной нагрузки постоянна и равна 
(направление этих сил показано на рис. 15.22,б стрелками).
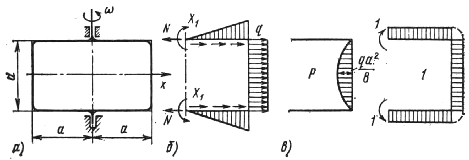
Рис. 15.22
Основную
систему выберем, рассекая раму по вертикальной оси симметрии. Из условия
симметрии системы относительно вертикальной и горизонтальной осей следует, что
в сечениях по вертикальной оси симметрии
перерезывающие силы равны нулю, осевые силы согласно уравнению 
будут
Для определения неизвестных изгибающих моментов X1 в этих сечениях составим каноническое уравнение
коэффициенты которого вычислим способом Верещагина. Перемножая эпюры от внешних и единичных сил (рис. 15.22), получаем
Подставляя
значения и в каноническое уравнение и решая его
относительно X1, имеем X1=qa2/36.
Суммируя изгибающие моменты в сечениях рамы от заданной нагрузки и X1, строим эпюру изгибающих моментов (рис. 15.23). Опасными являются сечения рамы, расположенные на горизонтальной оси симметрии, изгибающие моменты в которых
Рис. 15.23
Вопросы
для самопроверки
- Чем принципиально отличаются расчет статических и динамических систем?
- Какие нагрузки называют
динамическими?
- Как определяют величины
динамических напряжений?
- Что полагается в основу при
выводе формул для определения перемещений при ударе?
- Влияет ли модуль продольной
упругости на величину динамических напряжений? Обоснуйте.
- Как определяется нормальное напряжение в сечения тела, движущегося поступательно?
- Как ведется расчет троса грузоподъемного устройства?
- Как определяется напряжение в сечениях равномерно вращающегося кольца?
- Дайте определение инерционных нагрузок.
- На каком принципе основан расчет на прочность деталей с учетом сил инерции? В чем этот принцип заключается?
- Что такое коэффициент динамичности нагрузки?
- Что следует предпринять, чтобы динамический коэффициент снизить?
- Какой вид имеет формула
динамического коэффициента при ударе?
- Условие прочности при динамических нагрузках.
- Какая нагрузка называется ударной?
- Охарактеризуйте предпосылки, которые используются в расчетах на удар?
- Опишите методику решения задач при ударе?
- Как определяются напряжения при ударе?
- На каких допущениях основан расчет деталей на прочность при ударе?
- В какой последовательности вычисляют динамические напряжения и перемещения, возникающие в детали при ударе?
- Как подсчитывается динамический коэффициент при поперечном ударе по балке?
- Как определяется наибольшее нормальное напряжение в сечении балки, если она совершает колебательное движение?
- Может ли быть коэффициент динамичности нагрузки меньше единицы?
- Как произвести расчёт на прочность тонкостенного вращающегося кольца?
- Как определить напряжения и перемещения, возникающие при ударном действии нагрузки?
- Как определяется величина динамического коэффициента, если высота падения ударяющего тела значительно больше статического перемещения бруса в точке удара?
- Чему равен динамический коэффициент при внезапном приложении к детали нагрузки?
- Как определить динамический коэффициент при внезапном приложении к детали нагрузки?
- Как определить динамический коэффициент при ударе по упругой системе горизонтально движущимся телом?
- Как уменьшить динамические нагрузки и напряжения, возникающие в элементах конструкции при ударах?
- Чем объяснить, что при ковке берут массивную наковальню?
- Чем объяснить то, что при прыжках с высоты человек интуитивно сгибает в коленях ноги?
Онлайн-калькулятор "Расчет коэффициента динамичности при падении груза на конструкцию"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
