Главная
Лекция 21. Концентрация
напряжений и контактные напряжения
Содержание
Понятие о концентрации напряжений
Понятие о концентрации напряжений
Полученные ранее формулы для определения напряжений при растяжении, кручении и изгибе справедливы только в том случае, когда рассматриваемое сечение отстоит на достаточно большом расстоянии от мест резкого изменения формы тела, внутренних углов, выточек, отверстий и т.п. В окрестности выточек, отверстий и т.д., а также в зоне контакта деформируемых тел наблюдается концентрация напряжений.
Концентрацией напряжений называется увеличение напряжений в малых областях, примыкающих к местам с резким изменением формы поверхности тела, размеров его сечения или с локализованной неоднородностью материала внутри тела. Реальные конструкции всегда имеют зоны, в которых проявляется локальная концентрация напряжений. Конструкционные особенности деталей, вызывающие концентрацию напряжений, принято называть концентраторами напряжений. Примером таких концентраторов может служить корень зуба шестерни (рис.21.1, а); шпоночный паз вала (рис.21.1, б); резьба болта (рис.21.1, в); уступ вала (рис.21.1, г); заклепочное или болтовое соединение (рис.21.1, д); сварное соединение (рис.21.1, е) и др.
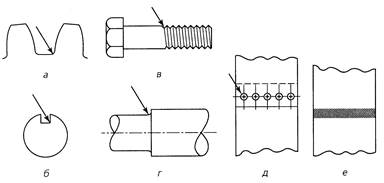
Рис.21.1
Анализ разрушений изделий показывает, что подавляющее большинство поломок, образование хрупких, усталостных трещин и других причин потери несущей способности возникают, как правило, вблизи этих концентраторов.
Явление концентрации напряжений объясняется тем, что в сплошном теле усилия передаются по возможно более короткому пути, что обеспечивает минимум внутренней энергии тела при данном нагружении. В результате материал, прилегающий к ослабленному месту, воспринимает дополнительные усилия, передающиеся с материала, окружающего отверстие или вырез.
Концентраторы напряжений можно разделить на локальные и размытые. К локальным будем относить те, в которых объем области, занятой материалом с повышенными напряжениями, пренебрежимо мал по сравнению со всем объемом нагруженного тела. В случае размытых концентраторов напряжений объем, занятый материалом с повышенными напряжениями, составляет значительную часть всего объема нагруженного тела. Таким образом при локальной концентрации напряжений общие размеры и форма всего нагруженного тела не будут существенно меняться в случае текучести материала в зоне концентрации, тогда как при размытой концентрации напряжений, они существенно изменяются. Например, малые отверстия и скругления малого радиуса считаются обычно весьма локальными концентраторами напряжений, а крюки, шарнирные соединения серег с проушинами относятся к размытым концентраторам напряжений. Последствия влияния различных концентраторов напряжений на материал в хрупком и пластичном состояниях при статическом и циклическом нагружении в виде коэффициентов концентрации напряжений представлены в таблице 21.1.
В последнем столбце таблицы в качестве коэффициентов концентрации напряжений указаны величины Kσ, ασ и Kτ. Дадим определения этим коэффициентам. Kσ - эффективный коэффициент концентрации напряжений в пластической области, равный отношению максимального действующего напряжения с учетом перераспределения напряжений за счет пластического деформирования, и номинального нормального напряжения σном для ослабленного сечения без учета концентрации напряжений. ασ - теоретический коэффициент концентрации напряжений, применимый только для упругой области нагружения. Концентрация напряжений при циклическом нагружении учитывается с помощью эффективного коэффициента концентрации напряжений Kτ или Kσ.
Таблица 21.1
|
Тип концентратора напряжений |
Вид нагружения |
Тип материала |
Вид разрушения |
Коэффициент концентрации напряжений |
|
Размытый |
Статическое |
Пластичный |
Большая область текучести |
Kσ |
|
Размытый |
Статическое |
Хрупкий |
Хрупкое разрушение |
ασ |
|
Размытый |
Циклическое |
Любой |
Усталостное разрушение |
Kτ |
|
Локальный |
Статическое |
Пластичный |
Перераспределе- ние напряжений без разрушения |
1 |
|
Локальный |
Статическое |
Хрупкий |
Хрупкое разрушение |
ασ |
|
Локальный |
Циклическое |
Любой |
Усталостное разрушение |
Kτ |
Рассмотрим растяжение длинной упругой полосы, ослабленной выточками (рис.21.2). В сечении 1-1 напряжения распределены равномерно, а в сечении 2-2 – неравномерно, увеличиваясь по мере приближения к краю выточек. Максимальное напряжение в этом сечении можно выразить так:
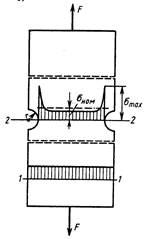
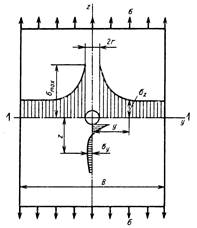
Рис.21.2
Рис.21.3
За номинальное напряжение 
принимают напряжение, которое определяется по
формулам сопротивления материалов без учета эффекта концентрации. Обычно определяется по наиболее ослабленному сечению.
Так, для рассмотренной полосы
где 
- площадь
полосы в ослабленном сечении 2-2.
Если определение напряжений в ослабленном
сечении затруднено, для простоты расчета за принимают напряжение в неослабленном сечении.
Значения теоретического коэффициента
концентрации напряжений 
практически не зависит от уровня номинальных
напряжений и физико-механических свойств материала, а определяются геометрией
рассматриваемого элемента, способом нагружения и
относительными размерами зон концентрации.
В теории упругости дается решение для растянутой пластинки, ослабленной круглым отверстием, расположенным на оси симметрии (рис.21.3).
Если ширина пластинки велика по сравнению с
радиусом отверстия r, то в наиболее ослабленном сечении 1-1 напряжение 
определяется по формуле
где σ - среднее напряжение в сечении, достаточно удаленном от места ослабления; y - расстояние от центра отверстия до точки, в которой определяется напряжение.
При y=r, 
. Таким образом, при 
.
С увеличением y напряжения быстро убывают, асимптотически приближаясь к напряжению σ.
В окрестности отверстия имеет место двухосное напряженное состояние. Так, в точках, лежащих на оси z, на вертикальных площадках возникают сжимающие напряжения, которые определяют по формуле
При
z = r, 
; при z = 2r,
. Как видно из эпюры (рис.21.3), эти
напряжения быстро затухают.
Приведенное точное решение может быть использовано лишь для пластинки, ширина которой велика по сравнению с диаметром отверстия (B≥10r). С уменьшением ширины пластинки теоретический коэффициент концентрации напряжений возрастает, а напряжения у наружных краев пластинки становятся меньше σ.
В таблице 21.2 приведены значения
коэффициента для
различных значений отношения диаметра отверстия к ширине пластинки.
Таблица 21.2
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
3,00 |
3,03 |
3,14 |
3,36 |
3,74 |
4,32 |
Как видно, коэффициент заметно увеличивается по мере увеличения
отношения 
.
Чтобы получить представление о степени
снижения напряжения на
краю пластины в сечении 1-1, приведем его значение для случая B=4r: 
. Для сравнения запишем значение
максимального напряжения в том же сечении: 
.
Концентрация напряжений как при растяжении, так и при других видах деформаций значительно зависит от формы отверстия или выточки.
Рассмотрим случай ослабления широкой пластинки эллиптическим отверстием (рис.21.4). Решение было получено Инглисом в 1913 г.
Точное решение представляется в виде
где a и b - полуоси эллипса.
С увеличением отношения 
максимальные напряжения возрастают и при узком
отверстии, расположенном перпендикулярно направлению растяжения, достигают
очень большого значения. В связи с этим большую опасность представляют тонкие
прорези. Особенно большие напряжения возникают у краев поперечных трещин.
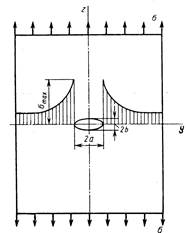
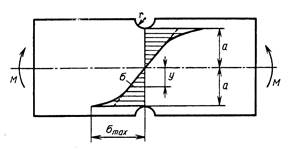
Рис.21.4
Рис.21.5
Концентрация напряжений возникает также при других видах деформаций. Так, например, при чистом изгибе полосы, ослабленной двумя симметричными выточками, имеющими форму гиперболы (рис.21.5), теоретический коэффициент концентрации напряжений может быть найден по формуле
где a- полуширина полосы в месте ослабления; r - радиус кривизны в глубине выточки.
Этой же формулой можно пользоваться для выточек другой формы, так как существенное влияние на коэффициент концентрации оказывает только кривизна у дна выточки. Так, например, с достаточной степенью точности эта формула может быть применена для выточек, показанных на рис. 21.6, а, б.
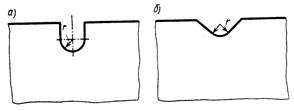
Рис.21.6
Необходимо помнить, что только для некоторых задач о концентрации напряжений найдены точные аналитические решения. В последнее время в связи с широким применением ЭВМ для решения задач теории упругости и использованием численных методов оказывается возможным найти теоретический коэффициент концентрации напряжений с достаточной для практических целей точностью для многих очагов концентрации напряжений. Найденные коэффициенты в упругой области для различных типов конструктивных элементов можно найти в справочниках по концентрации напряжений, нормах, технических условиях на проектирование конструкций и в других аналогичных источниках.
В других случаях, не поддающихся даже численному решению задачи, для определения коэффициентов концентрации напряжений и закона распределения напряжений применяются экспериментальные методы: фотоупругости, голографической интерферометрии, тензометрии, муаровых полос и др. В частности, при использовании оптического метода из специального материала изготовляют образец, который подвергается просвечиванию поляризованным светом при деформации. Расшифровка картины изохромовых полос позволяет установить наиболее напряженные точки и с достаточно высокой степенью точности определить коэффициент концентрации напряжений.
Следует обратить внимание на одну
принципиальную трудность решения задачи о концентрации напряжений. Обратимся к
формуле (21.2), из которой видно, что при 
выточка имеет форму острого угла, в вершине
угла напряжения равны бесконечности. В действительности вследствие проявления
пластических свойств материала напряжения в бесконечность не обращаются, но
достигают больших значений. Для деталей из идеально упругопластического
материала, для которого справедлива диаграмма Прандтля, концентрация напряжений
может не представлять особой опасности. Это объясняется тем, что при достижении
пластического состояния в точке напряжения в ней не увеличиваются и текучесть
материала распространяется в глубь сечения. Таким
образом, происходит выравнивание напряжений в ослабленном сечении. Анализ
напряженного состояния в зоне концентрации напряжений в этом случае требует
решения задачи теории пластичности, что представляет более серьезную проблему,
нежели решение аналогичной задачи теории упругости.
В случае хрупких материалов при достижении в ослабленном сечении наибольшего напряжения, равного пределу прочности, образуется трещина, которая, быстро развиваясь, приводит к разрушению конструкции. Так, например, небольшая царапина или надрез на стекле приводит к разрушению при весьма малых нагрузках по сравнению с теми, которые выдерживают стекло с неповрежденной поверхностью. Это свойство используют при резке стекол алмазом.
Нужно отметить, что опасность концентрации напряжений значительно возрастает при снижении температуры, поскольку материал становится более хрупким.
Критерием чувствительности материала к
концентрации напряжений является эффективный коэффициент концентрации
напряжений 
, равный отношению предела прочности гладкого
образца 
к условному пределу прочности надрезанного образца 
. Условный предел прочности надрезанного
образца равен отношению предельной нагрузки, выдерживаемой образцом с надрезом,
к площади наименьшего сечения образца. Следует отметить, что эффективный коэффициент
концентрации напряжений является условной характеристикой, поскольку зависит не
только от свойств материала, но и геометрии образца и способа его нагружения. Поэтому результаты испытания надрезанный
образцов не могут быть непосредственно перенесены на конструкцию произвольной
формы и размеров с концентраторами различной формы.
При наличии концентрации напряжений
существенно снижается деформация образца с концентратором по сравнению с
деформацией гладкого образца. Это связано с локализацией деформации у
концентратора напряжений. Одновременно происходит изменение характера
напряженного состояния у концентратора от осевого растяжения к объемному
растяжению и снижению, в связи с этим, 
, что в конечном
счете приводит к охрупчиванию материала конструкции.
Особенно опасна концентрация напряжений при действии нагрузок, периодически меняющихся во времени.
Наиболее острым концентратором напряжений
является трещина. Испытание образцов с исходной трещиной позволяет наиболее
жестко провести оценку чувствительности материала к концентратору напряжений.
На основе испытания образцов с исходной трещиной развивается механика
разрушения, рассматривающая поведение материалов с исходной трещиной и
позволяющая количественно оценивать сопротивление материала разрушению. В этих
испытаниях определяются такие характеристики трещиностойкости
материала, как критический коэффициент интенсивности напряжений 
(вязкость разрушения), критическое раскрытие в
вершине трещины 
, инвариантный 
-интеграл (упругопластическая
вязкость разрушения), диаграмма усталостного разрушения.
Возникает вопрос о том, каким образом можно снизить концентрацию напряжений.
Из приведенных выше формул для коэффициентов концентрации напряжений видно, что в различного рода трещинах, вырезах, выточках, в местах резкого изменения площади поперечного сечения элемента конструкции желательно заменить острые выточки плавными кривыми (галтелями), т.е. увеличить радиус кривизны конца трещины или отверстия. Это приводит к снижению концентрации напряжений. Так, например, для прекращения развития трещины в пластинах иногда на конце трещины высверливают круглое отверстие.
Контактные напряжения
Задачу определения напряжений, возникающих при сжатии двух соприкасающихся тел, называют контактной, а напряжения, возникающие по площадкам контакта, - контактными.
При сжатии двух тел, имеющих гладкую криволинейную поверхность, в зоне контакта происходит соединение точек поверхностей этих тел. В результате образуется поверхность, называемая поверхностью давления (пятном контакта), а ее контур – контуром давления. По поверхности давления действуют сжимающие напряжения. Расчет общей прочности тел в сечениях, удаленных о места контакта, ведется в соответствии с принципом Сен-Венана без учета особенностей распределения напряжений в зоне контакта. Для определения же местной прочности тела вблизи от точки соприкосновения первостепенную роль играют закон распределения напряжений в зоне контакта и значение максимальных контактных напряжений.
Материал, расположенный непосредственно под
зоной контакта, находится в объемном напряженном состоянии, так как сжатие в
направлении нормали к площадке контакта (напряжение 
на
рис.21.7) вызывает расширение объема материала в направлениях, параллельных
площадке.
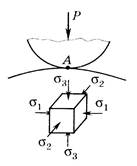
Рис.21.7
Поскольку рассматриваемый объем окружен
недеформированным материалом, сопротивляющимся расширению, по граням
рассматриваемого элемента возникают сжимающие напряжения 
и 
. Эти напряжения, конечно, меньше основных
сжимающих напряжений , но все же достаточно велики, чтобы
оказывать влияние на местную прочность в зоне контакта. В частности, наличие и , имеющих тот же знак, что и , ведет к уменьшению касательных напряжений 
и
повышению сопротивления материала развитию пластических деформаций. В связи с
этим материалы в состоянии выдерживать контактные напряжения, в несколько раз
превышающие предел прочности при
простом сжатии. Для некоторых сталей разрушающие контактные напряжения
достигают 3000-4000 МПа при =500-800 МПа.
Разрушение под влиянием контактных напряжений называется смятием материала. В отличие от сжатия при смятии разрушается лишь тонкий поверхностный слой материала в зоне контакта.
Расчет на смятие носит условный характер, так как точное определение напряжений и площадки контакта представляет собой сложную задачу. Напряжения зависят от радиусов кривизны соприкасающихся поверхностей и модулей упругости тел, нажимающих друг на друга. Уменьшение модуля упругости ведет к увеличению площади контакта, а следовательно, и к уменьшению напряжений.
Характерными примерами деталей, рассчитываемых на смятие, являются болты и заклепки, зубья шестерен, шейки и цапфы валов, детали шарикоподшипников. Взаимодействие упомянутых деталей обычно сводится к следующим схемам: надавливание сферы на сферу, сферы на плоскость, цилиндра на цилиндр, цилиндра на плоскость.
Рассмотрим данные случаи распределения напряжений в контактных задачах. Эти задачи решены с помощью методов теории упругости и в данном курсе приводятся без доказательства.
В общем случае, как показал Генрих Герц, контур давления является эллипсом. Напряжения в пределах поверхности давления распределены по полуэллипсоиду, причем на границе поверхности касания они равны нулю, а в центре напряжение принимает наибольшее значение
где F - сила, с которой тела давят друг на друга; a и b - длины полуосей эллиптического контура давления, значения которых зависят от геометрии поверхностей сдавливаемых тел, от модулей упругости и коэффициентов Пуассона материала этих тел, а также от силы F.
Как видно, значение 
в 1,5
раза больше среднего напряжения по поверхности касания:
Так,
при сжатии двух цилиндров радиусами 
и 
(рис.21.8, а,
б), загруженных нагрузкой, равномерно
распределенной по длине цилиндров, интенсивностью p, образуется поверхность
давления в виде прямоугольной полоски с размерами l×2b.
Если цилиндры сделаны из одного материала (
, 
, причем μ=0,3),
то
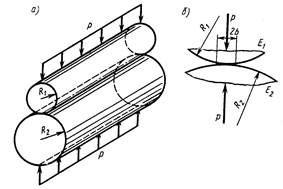
Рис.21.8
При неограниченном увеличении одного из
радиусов, например , получим решение задачи о сжатии цилиндра с
полупространством. В результате из выражений (21.3) и (21.4) получим
Как видно из формулы (21.5), наибольшее
напряжение зависит от отношения 
. При разных значениях p и
, но одинаковом их отношении также
одинаково.
Вычисленные по формуле (21.5) напряжения могут оказаться достаточно большими. Однако это еще не означает разрушения материала в зоне контакта. Дело в том, что в этой области имеет место пространственное напряженное состояние, в котором все три главных напряжения оказываются сжимающими. Поэтому расчетные сопротивления при местном смятии принимаются значительно бóльшими, чем при одноосном сжатии.
В случае центрального смятия двух упругих
шаров радиусами и (рис.21.9, а)
поверхность касания является кругом радиуса a (рис.21.9, б). Вновь предполагая справедливыми равенства , 
, получим
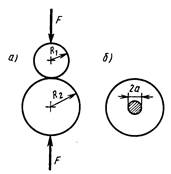
Рис.21.9
В случае шара радиусом , лежащего на упругом полупространстве (
), найдем
Из формулы (21.7) видно, что зависит от отношения 
. При разных значениях F и
, но одинаковых отношениях максимальное напряжение остается постоянным.
Если цилиндр радиусом лежит
на вогнутой цилиндрической поверхности радиусом или
шар радиуса находится на дне вогнутой сферической
поверхности радиуса (рис.21.10), то для определения можно
воспользоваться формулами (21.4) и (21.6), подставив в них отрицательное
значение (
). В итоге получим:
- для цилиндра
- для шара
Аналогично могут быть найдены напряжения при сдавливании тел и другой формы.
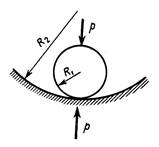
Рис.21.10
Контактные напряжения при статическом нагружении не могут вызвать разрушения, а приводят лишь к возникновению местных пластических деформаций. Однако при повторном действии нагрузок в зоне контакта может появиться трещина, которая, постепенно проникая в глубь детали, приводит к ее разрушению. Особенно нежелательно возникновение больших напряжений смятия между трущимися деталями, так как пластическое деформирование пятна контакта способствует усилению износа.
Вопросы для самопроверки
- Что такое концентрация напряжений?
- Что понимают под концентраторами напряжений? Привести примеры концентраторов напряжений и вычертить их.
- Что называют местными напряжениями?
- Как определить нормальные напряжения при осевом растяжении или сжатии по поперечному сечению стержня, достаточно удаленному от концентраторов напряжений и мест приложения сосредоточенных сил?
- Как распределяются нормальные напряжения при осевом растяжении или сжатии по поперечному сечению стержня, достаточно удаленному от концентраторов напряжений и мест приложения сосредоточенных сил?
- Как распределяются нормальные напряжения при осевом растяжении или сжатии по поперечному сечению стержня при наличии какого-либо концентратора напряжений?
- Описать характер распределения нормальных напряжений при осевом растяжении или сжатии по поперечному сечению полосы, ослабленному круглым отверстием.
- Можно ли определить напряжения при наличии концентраторов напряжений по формулам сопротивления материалов?
- Как определяются нормальные напряжения при осевом растяжении или сжатии по поперечному сечению стержня, ослабленному круглым отверстием (по какой формуле)?
- Что представляет собой теоретический коэффициент концентрации напряжений?
- Как определяется среднее (или номинальное) напряжение при вычислении теоретического коэффициента концентрации напряжений?
- Какие числовые значения имеет теоретический коэффициент концентрации?
- Как определить максимальное местное напряжение, зная теоретический коэффициент концентрации напряжений?
- Какими методами определяется теоретический коэффициент концентрации напряжений?
- От чего зависит концентрация напряжений?
- Какие меры принимаются для уменьшения концентрации напряжений?
- Почему концентрация напряжений при статическом нагружении конструкции менее опасна для пластичных материалов, чем для хрупких?
- Учитывается ли концентрация напряжений при расчете конструкций из пластичных и хрупких материалов?
- При наличии каких концентраторов в конструкциях из пластичных материалов всегда следует учитывать концентрацию напряжений?
- Учитывается ли концентрация напряжений для пластичных и хрупких материалов при действии динамических нагрузок?
- Как влияет радиус закругления выточки на коэффициент концентрации напряжений?
- Чему равны максимальные местные напряжения в полосе, ослабленной круглым отверстием (при h>10r)?
- Какова числовая величина теоретического коэффициента концентрации напряжений при ослаблении полосы круглым отверстием (при h>10r)?
- Какое влияние оказывают пластические свойства материала на концентрацию напряжений?
- Что такое контактные напряжения?
- Привести примеры распределения напряжений при наличии прорезов, выточек, уступов.
- Чем объясняется способность материала воспринимать достаточно высокие сжимающие напряжения в зоне контакта двух тел без разрушения?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
